Thiết kế bộ điều khiển tốc độ băng tải sử dụng điều khiển thích nghi mô hình tham chiếu hiệu chỉnh với toán tử tham chiếu

 thái 
của hệ thống băng tải * ( ))( d tux Ax B −= +& [13]. 
 Từ phương trình mô hình hóa hệ thống băng tải và các 
phương trình (21) tới (24) thì đạo hàm bậc nhất của e sẽ 
là: 
( ) ( )
( )
( ) ( )
( )
T T TI e u x r r dA B Km m
d d uBm
T TTI e x r r dA B Km m
d d uBm
e x x
m
λ
λ
= − + Λ − − − −Φ Ω
+ Λ − − Δ
= − + Λ − − −Φ Ω
+ Λ − − Δ
= −
&
%% %% &
& & &
 (25) 
Với ˆˆ ˆˆ, , , K K K d d d= − = − = − = −%% %%Φ Φ Φ Ω Ω Ω 
Bỏ qua ảnh hưởng của ngõ vào bão hòa chúng ta định 
nghĩa một véc tơ sai số phụ: 
ˆ( ) TI e uA Kme λ− − ΔΔΔ Δ=& (26) 
Với ( )IAm λ− là ma trận ổn định Hurwitz và 
3 3ˆ xK ∈ℜΔ là ma trận tham số thích nghi. 
 Véc tơ sai số phụ được sử dụng để bù vào véc tơ sai số 
trạng thái của ngõ vào bão hòa. Khi đó sẽ có một véc tơ 
sai số mới được định nghĩa như sau: 
ee eu = − Δ (27) 
 Theo các phương trình (25) tới (27) có thể tính được 
đạo hàm bậc nhất của eu như sau: 
( ) ( )
( )
ee eu
I e Kx r r dA Bm mu
T d dK u Bm
λ
= − Δ
= − + Λ −Φ −Ω −
+ Λ −Δ +
&& &
%% %% &
%
 (28) 
Với ˆT TK K Bm= − Λ%  
 Các ma trận độ lợi điều khiển ước lượng ˆ ˆˆ, ,K Φ Ω và 
véc tơ dˆ trong phương trình (14), có thể thay đổi nhỏ dưới 
tác dụng của nhiễu biên độ giới hạn. Vì vậy, bộ cập nhật 
luật điều khiển với các toán tử tham chiếu để làm giảm 
ảnh hưởng trên, sẽ được thiết kế như trong định lý 1. 
Định lý 1: Một bộ điều khiển M-MRAC cho hệ thống 
băng tải là ổn định, khi véc tơ ngõ vào điều khiển thiết kế 
theo (24), và bộ cập nhật luật điều khiển sử dụng một toán 
tử tham chiếu được cho bởi các phương trình: 
1
ˆ ˆProj( ,Y,f) γ=&Θ Θ (29) 
2
ˆ ˆProj(K,R,g) K γ=& &Δ 
(30) 3ˆ ˆProj(d(t),S,h) d γ=& (31) 
Trong đó: 1 2 3
T
T T TY Y Y Y
⎡ ⎤⎢ ⎥⎣ ⎦= với 1
T TY B Pe xum
= − , 
2
T TY B Pe rum
= − và 2 T TY B Pe rum= − & , 
Phạm Thế Duy, Nguyễn Huy Hùng 
ˆ ˆ ˆˆ 
T
T T TK⎡ ⎤= ⎢ ⎥⎣ ⎦
& & &&Θ Φ Ω , ˆ ˆ ˆˆ 
T
T T TK⎡ ⎤= ⎣ ⎦Θ Φ Ω , 
TuR PeuΔ= − , TS B Peum= − , 3f, g ∈ ℜ là các véc tơ 
hàm lồi, h là hàm lồi vô hướng và , , 01 2 3γ γ γ > là các độ 
lợi thích nghi. 
Chứng minh định lý 1: Chọn hàm Lyapunov để phân 
tích độ ổn định của hệ thống như sau: 
( ) ( )
( ) ( )
1
2 3
1
1 1 0
T T T T
u u
T T
V t e Pe trace K K
trace K K d d
γ
γ γΔ Δ
= + + +
+ + ≥
% % % %% %
% %% %
Λ Φ ΛΦ Ω ΛΩ
Λ
 (32) 
Lấy đạo hàm bậc nhất của ( )V t : 
( ) ( ) ( )
( ) ( ) ( )
( ) ( )
( )
2 ˆ ˆ( ) 2 1
1
2 ˆ ˆ 2 + 3
3
2 ˆ ˆ + (29)2
2
2* 2 01
TT
V t e Q P e trace Yu m u
TT
e PB d d d d d Su m
T
trace K K K R
e a e d eu u u
λ γγ
γγ
γγ
η
= − + + − −
+ − − −
− −
≤ − − ≤ ≤
⎡ ⎤⎢ ⎥⎣ ⎦
⎡ ⎤⎢ ⎥⎣ ⎦
&&
&
&
Θ Θ Λ Θ
Λ Λ
Δ Δ Δ
Trong đó: ( ) 2 ( ) 01 min minQ Pma λλ λ+ >= , ( )*d PB d d lm= Λ − ∈ ∞ và 01a η> > 
( )V t& sẽ có giá trị âm và bán xác định khi: 
*2*21 1
d
a e e edu u u a
η η− ≥ ⇒ ≥ − (34) 
 Điều này suy ra ˆˆ ˆˆ, , , KK ΔΦ Ω và dˆ giới hạn từ (32) 
đến (34) và 0eu → cũng như t →∞ theo định lý 
Barbalat. Do đó, e e→ Δ và e giới hạn khi và chỉ khi eΔ 
cũng giới hạn. Giới hạn của eΔ được chứng minh như 
sau: 
Chọn hàm Lyapunov: 
( ( )) 0TW W e t e PeΔ Δ= ≥ (35) 
Sử dụng nguyên lý Rayleigh được: 
2 2
( ) ( )min maxP e W P eλ λ≤ ≤Δ Δ (36) 
Lấy đạo hàm bậc nhất theo thời gian của W được: 
( ) ˆ2 2
2
 1 3 2 3
T TW e Q P e e PK um
e a W
λ
λ λ λ
= − + − ΔΔ Δ Δ Δ
≤ − + ≤ +Δ
&
 (37) 
trong đó 3 ˆ2 0
T Te PK uλ Δ Δ= − Δ ≥ và ( )12 max 0
a
P
λ λ= > . 
Sử dụng bất phương trình Gronwall Bellman, phương trình 
(37) suy ra: 
( )( ) ( )3 32
2 2
0 expTe Pe W W t
λ λλλ λΔ Δ Δ
⎡ ⎤= ≤ − − +⎢ ⎥⎣ ⎦
e (38) 
Kết hợp phương trình (35) và (38) sẽ có: 
3
2
lim T
t
e Pe
λ
λΔ Δ→∞ ≤ (39) 
( ) 23 min
2
lim limT
t t
e Pe P e
λ λλ Δ Δ Δ→∞ →∞≥ ≥ (40) 
 ( )32 minlimt e P
λ
λ λΔ→∞ ≤ (41) 
Và điều này chứng minh rằng Δe bị giới hạn. 
2. Ràng buộc của véc tơ sai lệch, độ lợi hồi tiếp và tốc 
độ thích nghi. 
 Vì ˆˆ , dˆ ˆˆ, , , KK ΔΦ Ω giới hạn, nên sẽ tồn tại một 
hằng số β thỏa mãn bất đẳng thức sau: 
( )
( ) ( )
1
2 3
1
1 1
T T T
T T
trace K K
trace K K d d
γ
β
γ γ γΔ Δ
+ +
+ + ≤
% % % %% %
% %% %
Λ Φ ΛΦ Ω ΛΩ
Λ
 (42) 
Trong đóγ là giá trị cực đại của tập { } 1 2 3γ γ γ . 
Từ (32), (42) và nguyên lý Rayleigh có bất đẳng thức sau: 
( ) 2 max ( )Tu u uV t e Pe t e Pβ βλγ γ≤ + ≤ + (43) 
Để đạt được một giới hạn trên 
ue , một mức Lyapunov 
thiết lập được định nghĩa như sau: 
{ }*( , , , , , d):VL e K VKu= Φ Ω ≤Δ %% %% % (44) 
Trong đó:
 ( )
*
1
24
( )max 2
* dP
a
V
βλ γη= +− 
Sử dụng nguyên lý Rayleigh trong các phương trình (32), 
(43), (44) có bất đẳng thức sau: 
 ( )
( )
*
*
max 2
*
max
2
2
22
2
min min
 ( )min
4( ) ( )min
( ) 4
( ) ( )
T
u u
u
P e e Pe V V
d
P e P
a
P d
e
P Pa
λ
βλλ γη
λ β
η γλλ
≤ ≤ ≤
⇒ ≤ +−
⇒ ≤ −
Δ
Δ (45) 
Từ (34) và (45) suy ra: 
( ) ( )
* *2( )2 4max0 2( ) ( )min min
Pd d
eu
a P Pa
λ β
η γληλ
≤ ≤ ≤− −
 (46) 
Do đó, từ (27), (41), (46) eco1 thể đạt được giới hạn trên 
như sau: 
(33) 
THIẾT KẾ BỘ ĐIỀU KHIỂN TỐC ĐỘ BĂNG TẢI SỬ DỤNG ĐIỀU KHIỂN THÍCH NGHI MÔ HÌNH.. 
( )
*2( ) 4max 3
2 ( )( ) 2( ) minmin min
e e eu u
P d
PP Pa
λ β λ
λ λγλλ η
≤ +
≤
−
Δ
 (47) 
 Trong bất phương trình (47), giới hạn trên của
ue có 
thể giảm nếu độ lợi hồi tiếp λ và độ lợi thích nghi γ 
tăng. 
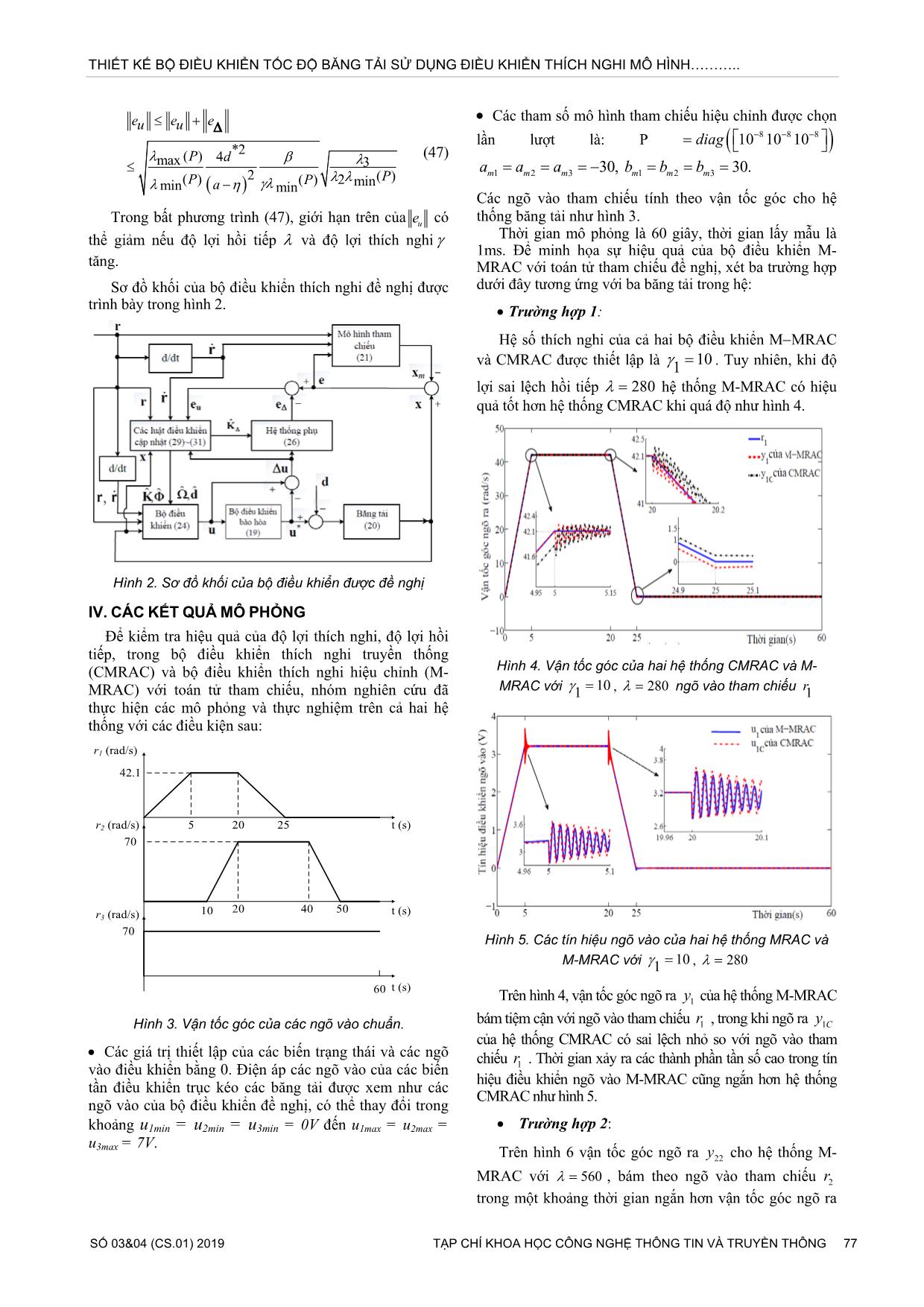
 Sơ đồ khối của bộ điều khiển thích nghi đề nghị được 
trình bày trong hình 2. 
Hình 2. Sơ đồ khối của bộ điều khiển được đề nghị 
IV. CÁC KẾT QUẢ MÔ PHỎNG 
Để kiểm tra hiệu quả của độ lợi thích nghi, độ lợi hồi 
tiếp, trong bộ điều khiển thích nghi truyền thống 
(CMRAC) và bộ điều khiển thích nghi hiệu chỉnh (M-
MRAC) với toán tử tham chiếu, nhóm nghiên cứu đã 
thực hiện các mô phỏng và thực nghiệm trên cả hai hệ 
thống với các điều kiện sau: 
t (s)
t (s)
t (s)
25
42.1
70
70
r1 (rad/s)
r2 (rad/s)
r3 (rad/s) 10
205
20 40
60
50
Hình 3. Vận tốc góc của các ngõ vào chuẩn. 
• Các giá trị thiết lập của các biến trạng thái và các ngõ 
vào điều khiển bằng 0. Điện áp các ngõ vào của các biến 
tần điều khiển trục kéo các băng tải được xem như các 
ngõ vào của bộ điều khiển đề nghị, có thể thay đổi trong 
khoảng u1min = u2min = u3min = 0V đến u1max = u2max = 
u3max = 7V. 
• Các tham số mô hình tham chiếu hiệu chỉnh được chọn 
lần lượt là: P ( )8 8 810 10 10diag − − −⎡ ⎤= ⎣ ⎦ 
1 2 3 1 2 330, 30.m m m m m ma a a b b b= = = − = = = 
Các ngõ vào tham chiếu tính theo vận tốc góc cho hệ 
thống băng tải như hình 3. 
Thời gian mô phỏng là 60 giây, thời gian lấy mẫu là 
1ms. Để minh họa sự hiệu quả của bộ điều khiển M-
MRAC với toán tử tham chiếu đề nghị, xét ba trường hợp 
dưới đây tương ứng với ba băng tải trong hệ: 
• Trường hợp 1: 
 Hệ số thích nghi của cả hai bộ điều khiển M−MRAC 
và CMRAC được thiết lập là 101γ = . Tuy nhiên, khi độ 
lợi sai lệch hồi tiếp 280λ = hệ thống M-MRAC có hiệu 
quả tốt hơn hệ thống CMRAC khi quá độ như hình 4. 
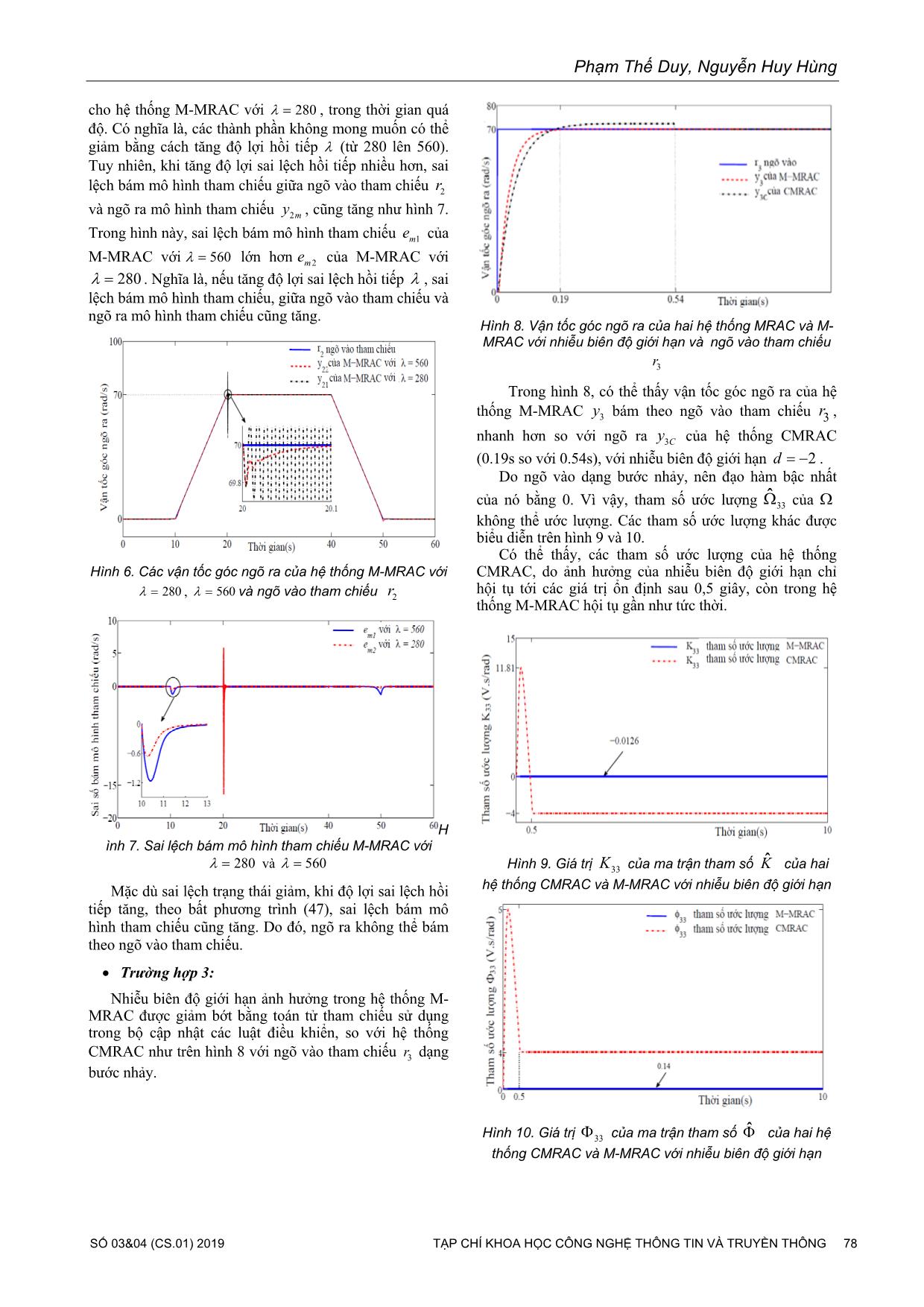
Hình 4. Vận tốc góc của hai hệ thống CMRAC và M-
MRAC với 101γ = , 280λ = ngõ vào tham chiếu 1r 
Hình 5. Các tín hiệu ngõ vào của hai hệ thống MRAC và 
M-MRAC với 101γ = , 280λ = 
Trên hình 4, vận tốc góc ngõ ra 1y của hệ thống M-MRAC 
bám tiệm cận với ngõ vào tham chiếu 1r , trong khi ngõ ra 1Cy 
của hệ thống CMRAC có sai lệch nhỏ so với ngõ vào tham 
chiếu 1r . Thời gian xảy ra các thành phần tần số cao trong tín 
hiệu điều khiển ngõ vào M-MRAC cũng ngắn hơn hệ thống 
CMRAC như hình 5. 
• Trường hợp 2: 
 Trên hình 6 vận tốc góc ngõ ra 22y cho hệ thống M-
MRAC với 560λ = , bám theo ngõ vào tham chiếu 2r 
trong một khoảng thời gian ngắn hơn vận tốc góc ngõ ra 
Phạm Thế Duy, Nguyễn Huy Hùng 
cho hệ thống M-MRAC với 280λ = , trong thời gian quá 
độ. Có nghĩa là, các thành phần không mong muốn có thể 
giảm bằng cách tăng độ lợi hồi tiếp λ (từ 280 lên 560). 
Tuy nhiên, khi tăng độ lợi sai lệch hồi tiếp nhiều hơn, sai 
lệch bám mô hình tham chiếu giữa ngõ vào tham chiếu 2r 
và ngõ ra mô hình tham chiếu 2my , cũng tăng như hình 7. 
Trong hình này, sai lệch bám mô hình tham chiếu 1me của 
M-MRAC với 560λ = lớn hơn 2me của M-MRAC với 
280λ = . Nghĩa là, nếu tăng độ lợi sai lệch hồi tiếp λ , sai 
lệch bám mô hình tham chiếu, giữa ngõ vào tham chiếu và 
ngõ ra mô hình tham chiếu cũng tăng. 
Hình 6. Các vận tốc góc ngõ ra của hệ thống M-MRAC với 
280λ = , 560λ = và ngõ vào tham chiếu 2r 
H
ình 7. Sai lệch bám mô hình tham chiếu M-MRAC với 
280λ = và 560λ = 
 Mặc dù sai lệch trạng thái giảm, khi độ lợi sai lệch hồi 
tiếp tăng, theo bất phương trình (47), sai lệch bám mô 
hình tham chiếu cũng tăng. Do đó, ngõ ra không thể bám 
theo ngõ vào tham chiếu. 
• Trường hợp 3: 
Nhiễu biên độ giới hạn ảnh hưởng trong hệ thống M-
MRAC được giảm bớt bằng toán tử tham chiếu sử dụng 
trong bộ cập nhật các luật điều khiển, so với hệ thống 
CMRAC như trên hình 8 với ngõ vào tham chiếu 3r dạng 
bước nhảy. 
Hình 8. Vận tốc góc ngõ ra của hai hệ thống MRAC và M-
MRAC với nhiễu biên độ giới hạn và ngõ vào tham chiếu 
3r 
 Trong hình 8, có thể thấy vận tốc góc ngõ ra của hệ 
thống M-MRAC 3y bám theo ngõ vào tham chiếu 3r , 
nhanh hơn so với ngõ ra 3Cy của hệ thống CMRAC 
(0.19s so với 0.54s), với nhiễu biên độ giới hạn 2d = − . 
 Do ngõ vào dạng bước nhảy, nên đạo hàm bậc nhất 
của nó bằng 0. Vì vậy, tham số ước lượng 33Ωˆ của Ω 
không thể ước lượng. Các tham số ước lượng khác được 
biểu diễn trên hình 9 và 10. 
 Có thể thấy, các tham số ước lượng của hệ thống 
CMRAC, do ảnh hưởng của nhiễu biên độ giới hạn chỉ 
hội tụ tới các giá trị ổn định sau 0,5 giây, còn trong hệ 
thống M-MRAC hội tụ gần như tức thời. 
 Hình 9. Giá trị 33K của ma trận tham số Kˆ của hai 
hệ thống CMRAC và M-MRAC với nhiễu biên độ giới hạn 
Hình 10. Giá trị 33Φ của ma trận tham số Φˆ của hai hệ 
thống CMRAC và M-MRAC với nhiễu biên độ giới hạn 
THIẾT KẾ BỘ ĐIỀU KHIỂN TỐC ĐỘ BĂNG TẢI SỬ DỤNG ĐIỀU KHIỂN THÍCH NGHI MÔ HÌNH.. 
V. KẾT LUẬN 
Bài báo đã đề nghị một bộ điều khiển tốc độ cho hệ 
thống băng tải, sử dụng mô hình thích nghi tham chiếu 
hiệu chỉnh (M-MRAC) với toán tử tham chiếu, để cải 
thiện hiệu suất trong trạng thái quá độ, và toán tử tham 
chiếu trong bộ cập nhật luật điều khiển làm hệ thống bền 
vững với nhiễu biên độ giới hạn. Ngoài ra bài báo cũng 
giải thích ràng buộc của sai lệch mô hình tham chiếu, độ 
lợi sai lệch hồi tiếp và độ lợi thích nghi. Khi độ lợi sai 
lệch hồi tiếp tăng, sai lệch trạng thái sẽ giảm và các thành 
phần tần số cao không mong muốn cũng giảm. Mặc dù 
véc tơ vận tốc góc ngõ ra bám theo tiệm cận với véc tơ 
vận tốc góc ngõ ra của mô hình hiệu chỉnh, sai lệch bám 
tham chiếu cũng tăng khi tăng độ lợi sai lệch hồi tiếp. Do 
đó, hiệu suất bám của bộ điều khiển đề nghị sẽ thấp, nếu 
độ lợi sai lệch hồi tiếp tăng rất nhiều. Hơn nữa, bộ cập 
nhật luật điều khiển với toán tử tham chiếu trong bộ điều 
khiển đề nghị, có thể giảm ảnh hưởng của nhiễu biên độ 
giới hạn từ các tham số ước lượng. 
LỜI CẢM ƠN 
 Nghiên cứu này được tài trợ bởi Học Viện Công nghệ 
Bưu chính Viễn thông (PTIT), cơ sở tại Thành Phố Hồ 
Chí Minh trong đề tài có mã số 05-HV-2019-RD_ĐT2. 
TÀI LIỆU THAM KHẢO 
[1] S. Thirachai, P. Komeswarakul, U. Supakchukul and J. 
Suwatthikul, “Trapezoidal velocity trajectory generator 
with speed override capability”, International Conference 
on Control Automation and Systems, 2010, pp. 1468-1472. 
[2] K. J. Astromn and B. Wittenmark, “Adaptive Control”, 
2nd ed. Dover publication, INC, 2008. 
[3] D.K. Le and T.K. Nam, “Optimal iterative learning control 
with model uncertainty”, Journal of the Korean Society of 
Marine Engineering, vol 37, no. 7, 2013, pp. 743-751. 
[4] V. T. Duong, J. H. Jeong, N. S. Jeong, M. S. Shin, T. T. 
Nguyen, G. S. Byun and S. B. Kim, “Cross-coupling 
synchronous velocity control for an uncertain model of 
transformer winding system using model reference 
adaptive control method”, Lecture Notes in Electrical 
Enginerring, vol. 371, 2016, pp. 441-455. 
[5] T. T. Nestorovic, H. Koppe, and U. Gabbert, “Direct 
model reference adaptive control (MRAC) design and 
simulation for the vibration suppression of piezoelectric 
smart structures”, Communications in Nonlinear Science 
and Numerical Simulation, vol. 13, no. 9, 2008, pp. 1896-
1909. 
[6] S. Karason and A. Annaswamy, “Adaptive Control in the 
Presence of Input Constraints”, IEEE Transactions on 
Automatic Control”, vol. 39, no. 11, 1994, pp. 2325-2330. 
[7] D. J. Wagg, “Transient bounds for adaptive control 
systems” IEEE Transactions on Automatic Control, vol. 
39, no. 1, 1994, pp. 171-175. 
[8] D. Y. Abramovitch, and G. F. Franklin, “On the stability of 
adaptive pole-placement controllers with a saturating 
actuator” IEEE Trans. on Automatic Control, vol. 35, no. 
3, 1990, pp. 303-306. 
[9] W. Sun, H. Gao and O. Kaynak, “Vibration isolation for 
active suspensions with performance constraints and 
actuator saturation, IEEE/ASME Transactions on 
Mechatronics, vol. 20, no. 2, 2015, pp. 675-683. 
[10] V. Stepanyan and K. Kalmanje, “Input and output 
performance of M-MRAC in the presence of bounded 
disturbances”, In: AIAA Guidance, Navigation, and 
Control Conference, 2010, pp. 2-5. 
[11] T. Gibson, A. Annaswamy and E. Lavretsky, “Adaptive 
systems with closed–loop reference models, Part I: 
Transient performance”, In: American Control Conf., 
2013, pp. 3376-3383. 
[12] V. T. Duong, T. H. Nguyen, T. T. Nguyen, J. M. Lee and 
S. B. Kim, “Modified model reference adaptive controller 
for a nonlinear SISO system with external disturbance and 
input constraint” Lecture Notes in Electrical Engineering, 
Vol. 415, 2016, pp. 118-128. 
[13] Pham The Duy, “Velocity control of conveyor belt system 
using model reference adaptive control method with 
saturated input” Hội nghị 20 năm thành lập Học viện Công 
nghệ Bưu chính Viễn thông. 
[14] Phạm Thế Duy, Phạm Việt Hùng,”Cải thiện khả năng bám 
cho bộ điều khiển MRAC của hệ thống điều khiển tốc độ 
băng tải” Journal of Science and Technology on 
Information and Communications (JSTIC) No. 01&02 
(CS.01) 2018/pp. 37-42 
BELL CONVEYOR VELOCITY CONTROLLER 
DESIGN USING MMRAC AND PROJECTION 
OPERATOR IN PRESENCE OF BOUNDED 
DISTURBANCES 
Abstract: The paper proposes a velocity controller using 
projection operator to reduce effectiveness of bounded 
disturbances is proposed, In addition, constraint of state 
error, the feedback error gain and adaptive gains are also 
presented to choose the suitable feedback error gain. The 
effectiveness of the proposed velocity controller is 
evaluated through simulation and experimental results. 
  Phạm Thế Duy 
Nhận học vị Thạc sĩ năm 1998 
Hiện công tác tại Học viện Công nghệ 
Bưu chính Viễn thông CS tại TP. 
HCM. 
Lĩnh vực nghiên cứu: Hệ thống nhúng, 
Kỹ thuật điều khiển và tự động hóa. 
Ảnh tác giả 
Nguyễn Huy Hùng 
Nhận học vị Tiến sỹ năm 2018 
Hiện công tác tại: Đại học Sài gòn 
Lĩnh vực nghiên cứu: Kỹ thuật điều 
khiển và tự động hóa, thông tin vô 
tuyến.