The Study of Spatial-Time-Frequency Correlation Properties of 5G Channel Modeling of MIMO-OFDM System

nith angle 𝜃 and the azimuth angle 𝜑. The multiple 
BSs and MSs are used in Global Coordinate System 
(GCS) and an array antenna for a BS/MS is used in 
Local Coordinate System (LCS), which is used as a 
reference to define the is pattern and polarization 
vector far-field of each antenna element in an array. 
The placement of an array within the GCS is 
occurred when translating between the GCS and the 
LCS by a sequence of rotations of the array with 
respect to the GCS. Therefore, it is necessary to map 
the vector fields of the array elements from the LCS to 
the GCS on which depends only on the orientation of 
the array. It leads that any arbitrary mechanical 
orientation of the array can be achieved by rotating the 
LCS with respect to the GCS. 
We defined a GCS with coordinates 
(𝑥, 𝑦, 𝑧, 𝜃 , 𝜙) and unit vectors ( �̂� , ϕ̂ ) and the LCS 
with "primed" coordinates (𝑥’, 𝑦’, 𝑧’, 𝜃′, 𝜙′) and 
"primed" unit vectors ( 𝜃′̂ , ϕ′̂ ). The arbitrary 3D-
rotation of the LCS with respect to the GCS given by 
the angles 𝛼 , 𝛽 and 𝛾, called the bearing angle, the 
down-tilt angle and the slant angle, respectively. 
Fig. 1. The Cartesian of 5G channel modeling [3] 
We set the �̇� axis is the original 𝑦 axis after the first 
rotation about 𝑧, and the �̈� axis is the original 𝑥 axis 
after the first rotation about 𝑧 and the second rotation 
about �̇�. 
A first rotation of α about 𝑧 sets the antenna bearing 
angle. The second rotation of 𝛽 about �̇� sets the 
antenna down-tilt angle. Finally, the third rotation of γ 
about �̈� sets the antenna slant angle. The orientation of 
the 𝑥, 𝑦, 𝑧 axes after all three rotations can be denoted 
as 𝑥, 𝑦, 𝑧. The angular ѱ now in charge of rotation to 
GCS is given as follow [3] and is illustrated in Fig. 2: 
ѱ =
= arg (
𝑠𝑖𝑛γcosθsin(ϕ − α) +
+cosγ(cosβsinθ − sinβcosθcos(ϕ − α)))
+𝑗(𝑠𝑖𝑛γ cos(ϕ − α) + sinβcosγ sin(ϕ − α))
) 
(1) 
Fig. 2. Rotation of LCS w/ respect of GCS [3] 
The simulators for 5G are defined and describe 
for channel model calibration in Table 1 - Table 3 as 
[3]: 
- UMi (Street canyon, open area) with O2O and 
O2I: the BSs are mounted below rooftop levels of 
surrounding buildings. UMi open area is intended to 
capture real-life scenarios in case of 50 to 100 m. 
- Indoor: This scenario is intended to capture 
various typical indoor deployment scenarios, including 
office environments, and shopping malls. The BSs are 
mounted at a height of 2-3 m either on the ceilings or 
walls. The shopping malls are often 1-5 stories high 
and several floors. 
- RMa: The rural deployment scenario focuses on 
larger and continuous coverage supporting high speed 
 Journal of Science & Technology 144 (2020) 011-016 
13 
vehicle with noise-limited and/or interference limited, 
using macro transmission reception points. 
Table 1. Parameters for UMi-street canyon [3] 
Parameters UMi -street canyon 
Cell layout 
Hexagonal grid, 19 
micro sites, 3 sectors 
per site ISD= 200m 
BS antenna height ℎ𝐵𝑆 10m 
UT 
loca 
-tion 
Outdoor/indoor Outdoor and indoor 
LOS/ NLOS LOS, NLOS 
Height ℎ𝑈𝑇 3D-UMi, TR36.873 
Indoor UT ratio 80% 
UT mobility (horizon) 3km/h 
Min. BS-UT distance 10m 
UT distribution Uniform 
Table 2. Parameters for indoor-office scenarios [3] 
Parameters InH open 
office 
mixed 
office 
Layout 
Room size 120𝑚 × 50𝑚 × 3𝑚 
ISD 20m 
BS antenna height ℎ𝐵𝑆 3 m (ceiling) 
UT 
location 
LOS/NLOS LOS and NLOS 
Height ℎ𝑈𝑇 1 m 
UT mobility (horizon) 3 km/h 
Min. BS - UT distance 0 
UT distribution (horizon) Uniform 
Table 3. Parameters for RMa [3] 
Parameters RMa 
Carrier Frequency Up to 7GHz 
BS height ℎ𝐵𝑆 35m 
Layout Hexagonal grid, 19 Macro 
sites, 3sectors per site, 
ISD = 1732m or 5000m 
UT height ℎ𝑈𝑇 1.5m 
UT distribution Uniform 
Indoor/Outdoor 50% indoor and 50% in car 
LOS/NLOS LOS and NLOS 
Min distance 2D 35m 
3. The properties of the correlation functions of the 
5G channel modelling in case of NLOS 
The specifications of NLOS 5G simulators define 
the impulse respond function ℎ(, ) of 𝑠 BS antenna 
elements and 𝑢 MS antenna elements [3]. 
ℎ𝑢,𝑠
𝑁𝐿𝑂𝑆(𝜏, 𝑡) = ∑∑ ∑ ℎ𝑢,𝑠,𝑛,𝑚
𝑁𝐿𝑂𝑆 (𝑡)𝛿(𝜏 − 𝜏𝑛,𝑖)
𝑚∈𝑅𝑖
3
𝑖=1
2
𝑛=1
+∑ℎ𝑢,𝑠,𝑛
𝑁𝐿𝑂𝑆(𝑡)𝛿(𝜏 − 𝜏𝑛)
𝑁
𝑛=3
(2) 
The transfer function 𝐻(, ) in frequency domain 
is the Fourier transform of ℎ(, ) the channel impulse 
response and is calculated with 𝜏𝑛 is the delay of the 
𝑛 cluster. 
𝐻𝑢,𝑠(𝑓, 𝑡) = ∑ℎ𝑢,𝑠(𝜏, 𝑡) × 𝑒
−𝑗2𝜋𝜏𝑛𝑓
𝑁
𝑛=1
(3) 
The spatial - temporal correlation function of 
2 × 2 antenna system is calculated by the time average 
operator as: 
𝜌(Δ𝑑𝑠, Δ𝑑𝑢 , Δ𝑡 , Δ𝑓 = 0) = 
〈𝐻𝑢1,𝑠1(𝑓, 𝑡) × 𝐻𝑢2,𝑠2
∗ (𝑓, 𝑡 + Δ𝑡)〉 =
= ∑√
𝑃𝑛
𝑀
∑
(
×
𝑒
𝑗2𝜋(�̂�𝑟𝑥,𝑛,𝑚
𝑇 ×Δ�̅�𝑟𝑥,𝑢)
𝜆0
×
𝑒
𝑗2𝜋(�̂�𝑟𝑥,𝑛,𝑚
𝑇 ×Δ�̅�𝑡𝑥,𝑠)
𝜆0
𝑒
𝑗2𝜋(�̂�𝑟𝑥,𝑛,𝑚
𝑇 ×�̅�)
𝜆0
Δ𝑡
)
𝑀
𝑚=1
𝑁
𝑛=1
(4) 
The correlation function can be done by using the 
average time of the two transfer functions. The channel 
correlation of is represented by the cross-correlation 
function in case of NLOS scenarios. The spatial-
temporal- frequency correlation functions of the 
transmitter and receiver MIMO 2 × 2 are calculated 
by the time average operation as in equation (5). The 
𝐹𝑟𝑥,𝑢,𝜃 , 𝐹𝑟𝑥,𝑢,𝜙 are the radiation field of the receive 
antenna element 𝑢 with direction �̂�, �̂�; 𝐹𝑡𝑥,𝑠,𝜃 , 𝐹𝑡𝑥,𝑠,𝜙 is 
the radiation field of transmit antenna element 𝑠 with 
direction �̂�, �̂�; �̂�𝑟𝑥,𝑛,𝑚
𝑇 is the spherical unit vector as the 
angle 𝜙𝑛,𝑚,𝐴𝑂𝐴 and 𝜃𝑛,𝑚,𝑍𝑂𝐴; �̂�𝑡𝑥,𝑛,𝑚
𝑇 is the spherical 
unit vector as the angle 𝜙𝑛,𝑚,𝐴𝑂𝐷 and 𝜃𝑛,𝑚,𝑍𝑂𝐷; �̅�𝑟𝑥,𝑢, 
�̅�𝑡𝑥,𝑠 is the location vector of antenna element u, s. 
Set Δ𝑑𝑠 = 0, Δ𝑑𝑢 = 0, the auto correlation 
(Temporal Correlation Function – TCF) is calculated 
as: 
𝜌(Δ𝑡) = ∑√
𝑃𝑛
𝑀
∑ exp (
𝑗2𝜋(�̂�𝑟𝑥,𝑛,𝑚
𝑇 × �̅�)
𝜆0
Δ𝑡)
𝑀
𝑚=1
𝑁
𝑛=1
(5) 
Set Δ𝑑𝑠 = 0, Δ𝑑𝑢 = 0 and Δ𝑡 = 0, the auto 
correlation (Frequency Correlation Function–FCF) is 
shown as: 
𝜌(Δ𝑓) = ∑√
𝑃𝑛
𝑀
𝑁
𝑛=1
exp (−𝑗2𝜋𝜏𝑛Δ𝑓) (6) 
Set Δ𝑡 = Δ𝑓 = 0 and Δ𝑑𝑢 = 0, the cross spatial 
correlation function of the channel at the transmitter is 
presented as: 
𝜌(Δ𝑑𝑠) = ∑√
𝑃𝑛
𝑀
∑ 𝑒
𝑗2𝜋(�̂�𝑡𝑥,𝑛,𝑚
𝑇 ×Δ�̅�𝑡𝑥,𝑠)
𝜆0
𝑀
𝑚=1
𝑁
𝑛=1
 (7) 
Similarity, the cross spatial correlation function 
at the receiver when Δ𝑡 = Δ𝑓 = 0 and Δ𝑑𝑠 = 0 is as 
follow: 
 Journal of Science & Technology 144 (2020) 011-016 
14 
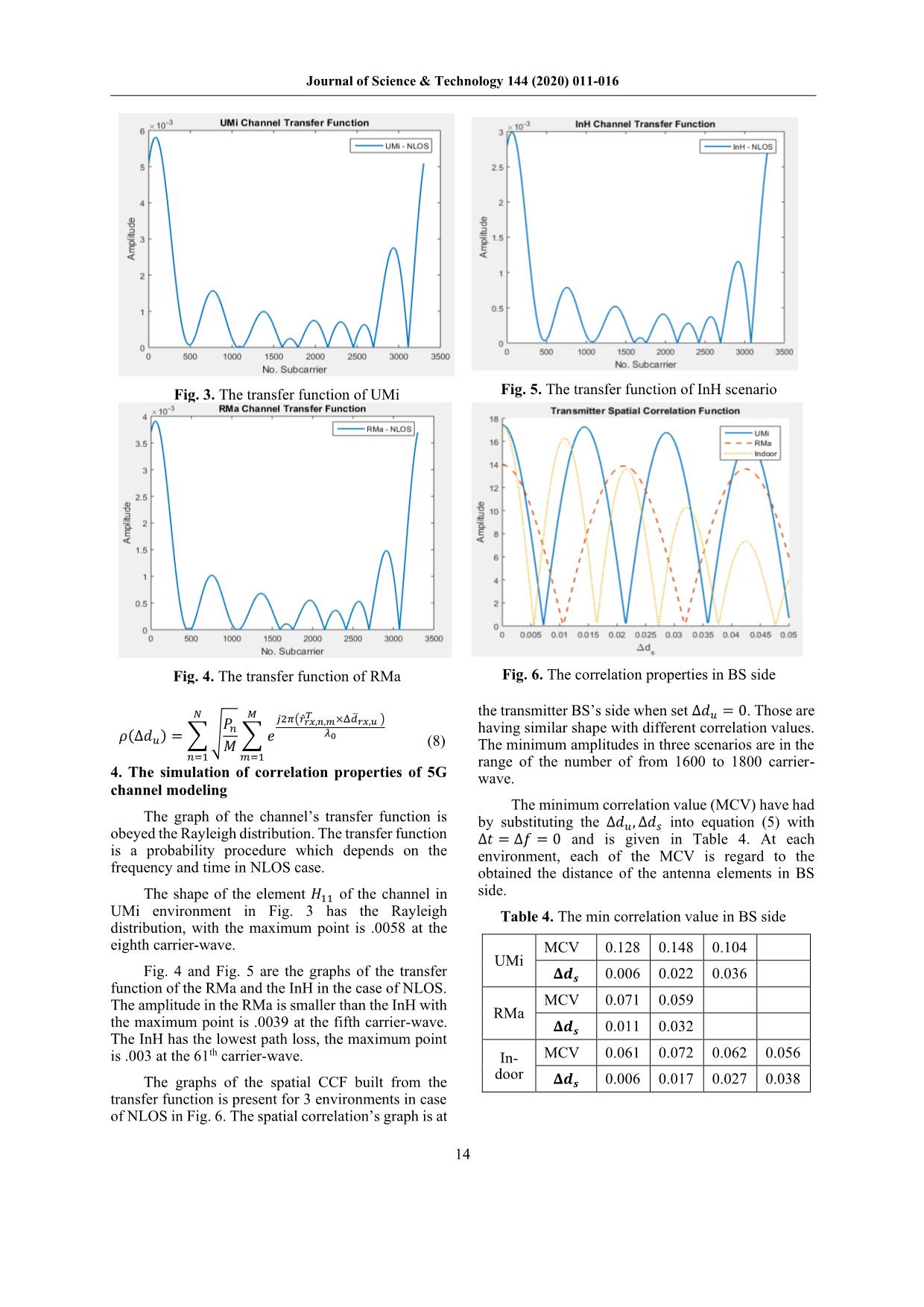
Fig. 3. The transfer function of UMi 
Fig. 5. The transfer function of InH scenario 
Fig. 4. The transfer function of RMa 
Fig. 6. The correlation properties in BS side 
𝜌(Δ𝑑𝑢) = ∑√
𝑃𝑛
𝑀
∑ 𝑒
𝑗2𝜋(�̂�𝑟𝑥,𝑛,𝑚
𝑇 ×Δ�̅�𝑟𝑥,𝑢 )
𝜆0
𝑀
𝑚=1
𝑁
𝑛=1
(8) 
4. The simulation of correlation properties of 5G 
channel modeling 
The graph of the channel’s transfer function is 
obeyed the Rayleigh distribution. The transfer function 
is a probability procedure which depends on the 
frequency and time in NLOS case. 
The shape of the element 𝐻11 of the channel in 
UMi environment in Fig. 3 has the Rayleigh 
distribution, with the maximum point is .0058 at the 
eighth carrier-wave. 
Fig. 4 and Fig. 5 are the graphs of the transfer 
function of the RMa and the InH in the case of NLOS. 
The amplitude in the RMa is smaller than the InH with 
the maximum point is .0039 at the fifth carrier-wave. 
The InH has the lowest path loss, the maximum point 
is .003 at the 61th carrier-wave. 
The graphs of the spatial CCF built from the 
transfer function is present for 3 environments in case 
of NLOS in Fig. 6. The spatial correlation’s graph is at 
the transmitter BS’s side when set Δ𝑑𝑢 = 0. Those are 
having similar shape with different correlation values. 
The minimum amplitudes in three scenarios are in the 
range of the number of from 1600 to 1800 carrier- 
wave. 
The minimum correlation value (MCV) have had 
by substituting the Δ𝑑𝑢 , Δ𝑑𝑠 into equation (5) with 
Δ𝑡 = Δ𝑓 = 0 and is given in Table 4. At each 
environment, each of the MCV is regard to the 
obtained the distance of the antenna elements in BS 
side. 
Table 4. The min correlation value in BS side 
UMi 
MCV 0.128 0.148 0.104 
𝚫𝒅𝒔 0.006 0.022 0.036 
RMa 
MCV 0.071 0.059 
𝚫𝒅𝒔 0.011 0.032 
In-
door 
MCV 0.061 0.072 0.062 0.056 
𝚫𝒅𝒔 0.006 0.017 0.027 0.038 
 Journal of Science & Technology 144 (2020) 011-016 
15 
Table 5. The min correlation value in MS side 
UMi MCV 0.051 0.085 
𝚫𝒅𝒔 0.011 0.029 
RMa MCV 0.013 0.064 
𝚫𝒅𝒔 0.009 0.028 
Indoor MCV 0.109 0.083 0.017 0.09 
𝚫𝒅𝒔 0.006 0.018 0.028 0.039 
Fig. 7. The correlation properties in MS side 
Fig. 7 are the illustration of spatial correlation 
functions in MS side. The amplitude of the UMi is 
highest and the RMa is lowest. 
As one can see, the distance of the antenna 
elements in the transmit side Δ𝑑𝑢 has the minimum at 
the 0.005 - 0.01. The minimum correlation value of 
UMi, RMa and Indoor are 0.011, 0.0094 and 0.0063, 
respectively. In the range of Δ𝑑𝑢 = 0 − 0.04, there 
are two minimum correlation values of the UMi and 
RMa, while the InH have 4 as in Table 5. That is, the 
InH scenarios is much more changeable than the 
others. 
Fig. 8. The temporal ACF of UMi 
The temporal ACF of UMi in Fig. 8 depends on 
the velocity of the movement of the MS. In case of the 
high velocity of the MS, the variation of the signal is 
strong based on the Doppler spectrum theory. We have 
three divergent MS velocity such as 3km/h with 
walking pavement, 60 km/h with vehicles in the street, 
300km/h with metro or high-speed rail. The high speed 
can be up to 500km/h as the 3GPP note. With 
pedestrian 5km/h, in the range of 10-3 s, the variation 
of the signal included the amplitude and phase is 
almost immutable. With vehicle moving 60km/h, in 
10-3 s, the signal shifts greatly with 3 peaks. But the 
most altering signal is at the high-speed rail 300km/h, 
which makes 12 peaks in 10-3 s. Therefore, when the 
MS moving with high speed, the Doppler effect leads 
to changing of the coherence time. 
The graph of the frequency ACF of UMi is in Fig 
9 with the shape of probability distribution, that is, the 
decreasing of the amplitude, the higher of the Δ𝑓. 
In the bandwidth of 0 – 0.07 (GHz), the 
minimum of the frequency are at Δ𝑓 = {0.0063,
0.0183, 0.0295, 0.0405, 0.0549, 0.0626, 0.0689}. 
Therefore, at each Δ𝑓 the frequency correlation value 
is equal to 0. That is at each minimum frequency 
correlation point, the affection of the frequency at BS 
and MS side is negligible. 
Fig. 9. The frequency ACF of UMi 
5. Conclusion 
We study the correlation properties of 5G 
channel modeling in MIMO 2 ×2 antenna system. The 
sets of temporal-spatial-frequency cross-correlation 
function are calculated and simulated in the scenarios 
of UMi, RMa and indoor NLOS cells at frequency 
band 6 GHz. Base on the built formulae, we determine 
the minimum correlation value at each MS, BS side. 
The MCVs depend on the distance elements of the 
antenna in each base station (BS) and mobile station 
(MS) side. We also identify the offset in time and 
frequency correlation functions to conclude that the 
signal is stable in each certain range. Based on the 
acquired correlation distinguishing, the simulations are 
at the system level of 5G channel modeling, leads to 
open more results to applied to uplink systems as well. 
We use Monte Carlo simulation method by Matlab 
programing. Our next research is estimating the 
 Journal of Science & Technology 144 (2020) 011-016 
16 
system performance of the MIMO-OFDM using the 
LDPC coding based on 5G channel modeling above. 
6. Acknowledgement 
This work was funded by the Vietnam’s Ministry 
of Education and Training (MOET) Project B2019-
BKA-10. 
References 
[1] Thu Nga Nguyen, Van Duc Nguyen, “A performance 
comparison of the SCM and the Onering channel 
modeling method for MIMO‐OFDMA systems”, in 
Wireless Communications Mobile Computing, 
Volume16, Issue17, 2016 
[2] 3GPP- TR 25.996 V10.0.0. Technical Specification 
Group Radio Access Network Spatial channel model 
for MIMO simulation, (2011-03), (2011). 
[3] ETSI TR 138 901 V14.0.0 (2017-05), 5G -Study on 
channel model for frequencies from 0.5 to 100 GHz 
(3GPP TR 38.901 version 14.0.0 Release 14) 
[4] Cheng-Xiang Wang, Ji Bian, Jian Sun, Wensheng 
Zhang and Minggao Zhang, ”A Survey of 5G Channel 
Measurements and Models” IEEE Communications 
surveys and tutorials, 2018 
[5] Basim Mohammed Eldowek, Saied, El. Rabaie, Fathi 
Samie, “3D Modeling and Analysis of the Space–Time 
Correlation for 5G Millimeter Wave MIMO 
Channels”, in Wireless Personal Communications · 
November 2018 
[6] Samimi, M. K., Sun, S., & Rappaport, T. S, “MIMO 
channel modeling and capacity analysis for 5G 
millimeter-wave wireless systems”, 10th European 
Conference on Antennas and Propagation (EuCAP) 
2016, doi:10.1109/eucap.2016.7481507 
[7] Omar E .Ayach, et al., “Spatially Sparse Precoding in 
Millimeter Wave MIMO Systems“, IEEE Transactions 
on Wireless communications Vol. 13, No. 3, March 
2014 
[8] Yawei Yu, et.al., “3D vs. 2D Channel Models: Spatial 
Correlation and Channel Capacity Comparison and 
Analysis”, IEEE ICC 2017 Wireless Communications 
Symposium 
[9] K. Haneda et al., “Indoor 5G 3GPP-like Channel 
Models for Office and Shopping Mall Environments,” 
to be published in 2016 IEEE International Conference 
on Communications Workshops (ICCW), May, 2016. 
[10] Shu Sun, et al., “Investigation of Prediction Accuracy, 
Sensitivity, and Parameter Stability of Large-Scale 
Propagation Path Loss Models for 5G Wireless 
Communications”, IEEE Transactions on Vehicular 
Technology, Vol 65, Issue 5, 2016. 
[11] K. Haneda et al., "Indoor 5G 3GPP-like channel 
models for office and shopping mall environments," 
2016 IEEE International Conference on 
Communications Workshops (ICC), Kuala Lumpur, 
2016, pp. 694-699. 
[12] T. S. Rappaport, et al., "Investigation and Comparison 
of 3GPP and NYUSIM Channel Models for 5G 
Wireless Communications," 2017 IEEE 86th 
Vehicular Technology Conference (VTC-Fall), 
Toronto, ON, 2017, pp. 1-5. 
[13] M. Rumney, P. Kyösti, L. Hentilä, "3GPP channel 
model developments for 5G NR requirements and 
testing," 12th European Conference on Antennas and 
Propagation (EuCAP 2018), London, 2018, pp. 1-5. 
[14] V. Díaz and D. M. Aviles, "A Path Loss Simulator for 
the 3GPP 5G Channel Models," 2018 IEEE XXV 
International Conference on Electronics, Electrical 
Engineering and Computing (INTERCON), Lima, 
2018, pp. 1-4 
 Journal of Science & Technology 144 (2020) 011-016 
17