Tài liệu ôn thi THPT Quốc gia môn Toán - Chuyên đề: Chiều biến thiên hàm số
Câu 39: Cho hàm số y f x có đạo hàm f x x x 2 1, . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng ;0.
B. Hàm số nghịch biến trên khoảng 1;.
C. Hàm số nghịch biến trên khoảng 1;1.
D. Hàm số đồng biến trên khoảng ; .
Câu 40: Cho hàm số y f x có đồ thị như hình vẽ. Mệnh đề nào dưới
đây là đúng?
A. Hàm số nghịch biến trên khoảng ;1.
B. Hàm số nghịch biến trên khoảng 1;.
C. Hàm số nghịch biến trên khoảng 1;1.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
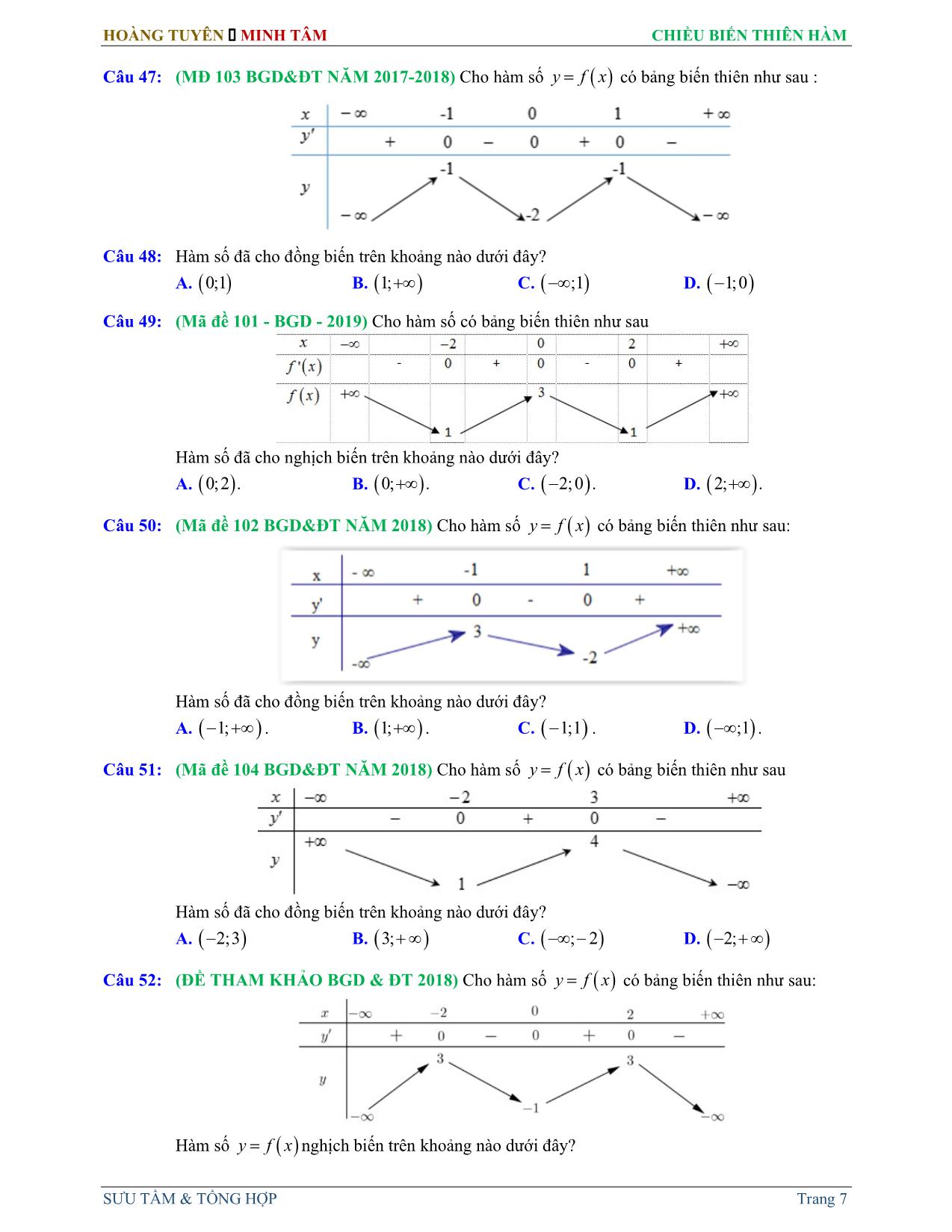
Trang 7

Trang 8
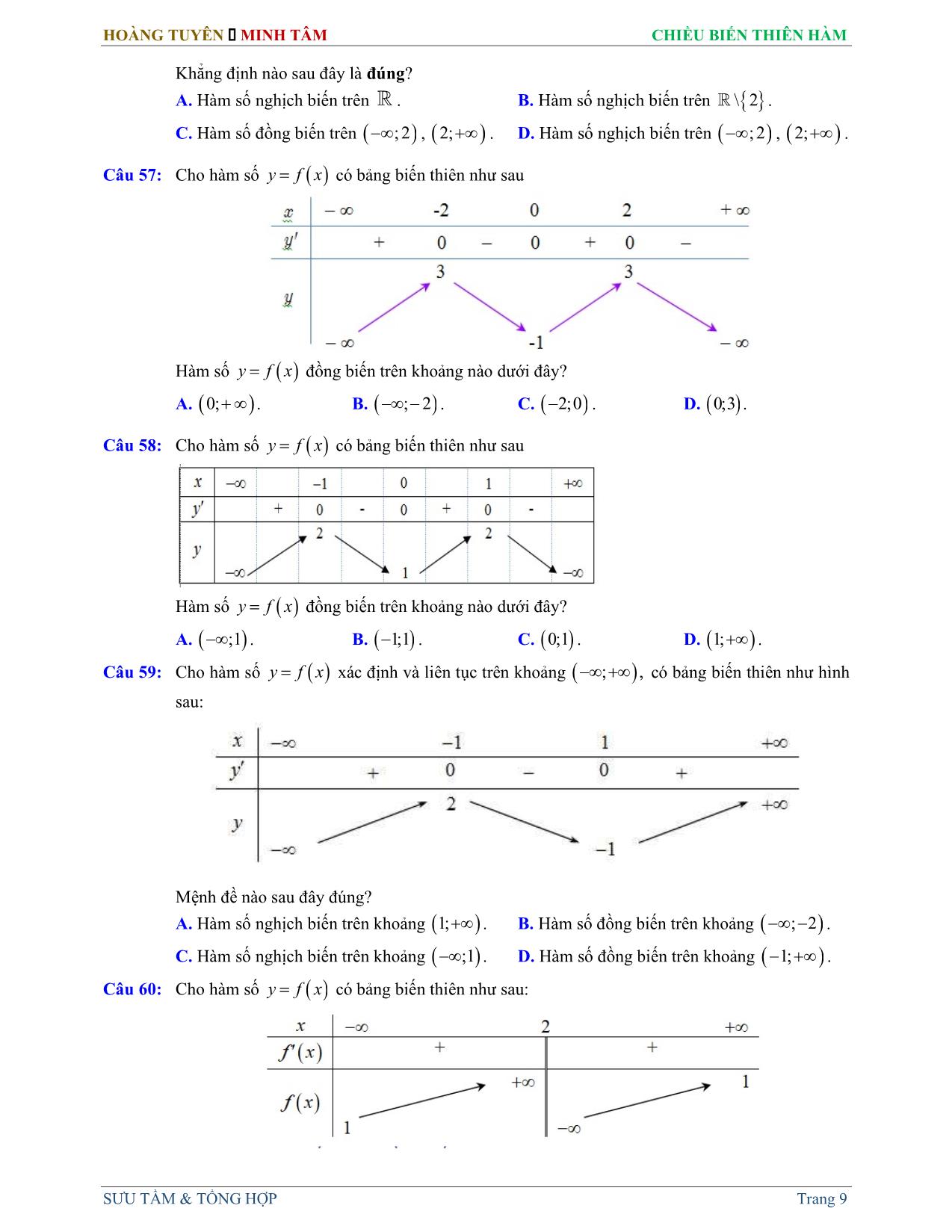
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Tài liệu ôn thi THPT Quốc gia môn Toán - Chuyên đề: Chiều biến thiên hàm số", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Tài liệu ôn thi THPT Quốc gia môn Toán - Chuyên đề: Chiều biến thiên hàm số

TUYÊN MINH TÂM CHIỀU BIẾN THIÊN HÀM SƯU TẦM & TỔNG HỢP Trang 37 DẠNG 5: XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM HỢP BÀI TOÁN 1: CHO BẢNG BIÊN THIÊN Câu 187: Cho hàm số y f x có bảng biến thiên Tìm các khoảng đồng biến của hàm số 2 1y f x . Câu 188: Cho hàm số y f x có bảng biến thiên Tìm các khoảng nghịch biến của hàm số 2 6y f x . Câu 189: Cho hàm số y f x có bảng biến thiên Hỏi hàm số 21 3 6 2 y f x x nghịch biến trên các khoảng nào? Câu 190: Cho hàm số y f x có bảng biến thiên CHIỀU BIẾN THIÊN HÀM SỐ HOÀNG TUYÊN MINH TÂM Trang 38 SƯU TẦM & TỔNG HỢP Tìm các khoảng đồng biến của hàm số 2 2y f x x ? Câu 191: Cho hàm số y f x có bảng biến thiên Hỏi hàm số y f f x đồng biến trên những khoảng nào? Câu 192: Cho hàm số y f x liên tục trên và có bảng biến thiên như sau Tìm các khoảng đồng biến của hàm số 3 254 2 6 1 3 2 xy g x f x x x . Câu 193: Cho hàm số y f x có bảng biến thiên Tìm các khoảng nghịch biến của hàm 5 2y f x ? Câu 194: Cho hàm số y f x có bảng biến thiên như sau HOÀNG TUYÊN MINH TÂM CHIỀU BIẾN THIÊN HÀM SƯU TẦM & TỔNG HỢP Trang 39 Hỏi hàm số 2 2y f x x nghịch biến trên các khoảng nào? Câu 195: Cho hàm số ( )y f x có bảng xét dấu đạo hàm như sau Hàm số 2( ) ( )g x f x nghịch biến trên khoảng nào? A. (0;1). B. (1; ). C. ( 1;0). D. ( ;0). Câu 196: Cho hàm số y f x liên tục trên và có bảng xét dấu đạo hàm như sau Biết 1 3f x , x . Hàm số 3 26 1y g x f f x x x có ít nhất bao nhiêu khoảng đồng biến? BÀI TOÁN 2: CHO ĐỒ THỊ F’(X) Câu 197: Cho hàm số y f x có đạo hàm trên và có đồ thị hàm số y f x như hình bên. Xét tính đơn điệu của hàm số 3y g x f x . Câu 198: Cho hàm số y f x có đạo hàm liên tục trên . Hàm số y f x có đồ thị như hình vẽ sau: CHIỀU BIẾN THIÊN HÀM SỐ HOÀNG TUYÊN MINH TÂM Trang 40 SƯU TẦM & TỔNG HỢP Tìm các khoảng đơn điệu của hàm số 1g x f x x . Câu 199: Cho hàm số y f x có đạo hàm liên tục trên . Đồ thị hàm số y f x như hình vẽ bên. Tìm các khoảng đồng biến của hàm số 2020g x f x x . Câu 200: Cho hàm số y f x . Hàm số y f x có đồ thị như hình vẽ. Hàm số 2y g x f x đồng biến trên khoảng nào? Câu 201: Cho hàm số .y f x Đồ thị hàm số y f x như hình bên. Hàm số 1 2g x f x đồng biến trên khoảng nào trong các khoảng sau? A. 1;0 . B. ;0 . C. 0;1 . D. 1; . Câu 202: Cho hàm số .y f x Đồ thị hàm số y f x như hình bên. Hỏi hàm số 2g x f x đồng biến trên khoảng nào trong các khoảng sau? A. ; 1 . B. 1; . C. 1;0 . D. 0;1 . Câu 203: Cho hàm số .y f x Đồ thị hàm số y f x như hình bên. Đặt 2 2 .g x f x Mệnh đề nào dưới đây sai? A. Hàm số g x đồng biến trên khoảng 2; . B. Hàm số g x nghịch biến trên khoảng 0;2 . C. Hàm số g x nghịch biến trên khoảng 1;0 . D. Hàm số g x nghịch biến trên khoảng ; 2 . Câu 204: Cho hàm số y f x . Đồ thị hàm số y f x như hình bên. Hỏi 2 5g x f x có bao nhiêu khoảng nghịch biến? A. 2 B. 3. C. 4. D. 5. O x y 1 1 1 2 1 HOÀNG TUYÊN MINH TÂM CHIỀU BIẾN THIÊN HÀM SƯU TẦM & TỔNG HỢP Trang 41 Câu 205: Cho hàm số .y f x Đồ thị hàm số y f x như hình bên. Hỏi hàm số 23g x f x đồng biến trên khoảng nào trong các khoảng sau? A. 2;3 . B. 2; 1 . C. 0;1 . D. 1;0 . Câu 206: Cho hàm số .y f x Đồ thị hàm số y f x như hình bên. Hỏi hàm số 2g x f x x nghịch biến trên khoảng nào trong các khoảng sau? A. 1;2 . B. ;0 . C. ;2 . D. 1 ; . 2 Câu 207: Cho hàm số y f x . Hàm số y f x có đồ thị như hình vẽ. Hàm số 2 4y g x f x nghịch biến trên khoảng nào? Câu 208: Cho hàm số f x liên tục trên và có đồ thị hàm số 'y f x như hình vẽ bên. Hàm số 2 5 4 xg x f x nghịch biến trên khoảng nào? Câu 209: Cho hàm số y f x . Hàm số y f x có đồ thị như hình vẽ. Hàm số 21 2y g x f x x đồng biến trên khoảng nào? CHIỀU BIẾN THIÊN HÀM SỐ HOÀNG TUYÊN MINH TÂM Trang 42 SƯU TẦM & TỔNG HỢP Câu 210: Cho hàm số .y f x Đồ thị hàm số y f x như hình bên. Hàm số 3 2g x f x nghịch biến trên khoảng nào trong các khoảng sau? A. 0;2 . B. 1;3 . C. ; 1 . D. 1; . Câu 211: Cho hàm số .y f x Đồ thị hàm số y f x như hình bên. Hỏi hàm số 2g x f x đồng biến trên khoảng nào? A. ; 2 . B. 2; 1 . C. 1;0 . D. 1;2 . Câu 212: Cho hàm số .y f x Đồ thị hàm số y f x như hình bên. Hỏi hàm số 21g x f x nghịch biến trên khoảng nào trong các khoảng sau? A. 1;2 B. 0; C. 2; 1 D. 1;1 Câu 213: Cho hàm số y f x . Hàm số y f x có đồ thị như hình vẽ. Hàm số 3y g x f x đồng biến trên khoảng nào? Câu 214: Cho hàm số y f x . Hàm số y f x có đồ thị như hình vẽ. Hàm số 2 2 2 y g x f x x đồng biến trên khoảng nào? HOÀNG TUYÊN MINH TÂM CHIỀU BIẾN THIÊN HÀM SƯU TẦM & TỔNG HỢP Trang 43 BÀI TOÁN 3: KẺ THÊM ĐƯỜNG PHỤ Câu 215: Cho hàm số y f x có đạo hàm liên tục trên và có đồ thị hàm số y f x như hình vẽ. Tìm các khoảng nghịch biến của hàm số 2( ) 2y f x x x . Câu 216: Cho hàm số y f x có đạo hàm liên tục trên và có đồ thị hàm số y f x như hình vẽ bên. Tìm các khoảng đồng biến của hàm số 22 ( ) 2 2019g x f x x x . Câu 217: Cho hàm số f x liên tục trên và có đồ thị hàm số 'y f x như hình vẽ bên. Hàm số 31 6 3 y f x x x đồng biến trên khoảng nào? Câu 218: Cho hàm số f x liên tục trên và có đồ thị hàm số 'y f x như hình vẽ bên. CHIỀU BIẾN THIÊN HÀM SỐ HOÀNG TUYÊN MINH TÂM Trang 44 SƯU TẦM & TỔNG HỢP Hàm số 33 g x f x x đồng biến trên khoảng nào? Câu 219: Cho hàm số y f x liên tục trên . Hàm số y f x có đồ thị như hình vẽ. Hàm số 2019 20181 2018 xy g x f x đồng biến trên khoảng nào? Câu 220: Cho hàm số y f x có đạo hàm liên tục trên và có đồ thị hàm số y f x như hình vẽ. Tìm các khoảng đồng biến của hàm số 2 1 1 2 4y g x f x x x . Câu 221: Cho hàm số y f x có đạo hàm liên tục trên . Đồ thị hàm số y f x như hình bên dưới O x y 1 1 1 2 1 HOÀNG TUYÊN MINH TÂM CHIỀU BIẾN THIÊN HÀM SƯU TẦM & TỔNG HỢP Trang 45 Hàm số 3 272 12 1 3 2 xg x f x x x có ít nhất bao nhiêu khoảng nghịch biến? Câu 222: Cho hàm số y f x có đồ thị f x như hình vẽ Hàm số 2 1 2 xy f x x nghịch biến trên khoảng nào? Câu 223: Cho hàm số y f x có đạo hàm liên tục trên . Đồ thị hàm số y f x như hình bên dưới. Hàm số 22y g x f x x đồng biến trên các khoảng nào? Câu 224: Cho y f x có đạo hàm liên tục trên . Đồ thị hàm số y f x như hình bên. Hàm số g x f x x đồng biến trên khoảng nào? A. ; 1 B. 0;1 C. 1;1 D. 1; Câu 225: Cho y f x có đạo hàm liên tục trên . Đồ thị hàm số y f x như hình bên. Hàm số 33g x f x x nghịch biến trên khoảng nào? A. 2;0 B. ; 2 C. 0;1 CHIỀU BIẾN THIÊN HÀM SỐ HOÀNG TUYÊN MINH TÂM Trang 46 SƯU TẦM & TỔNG HỢP D. 0; Câu 226: Cho hàm số y f x với đạo hàm f x có đồ thị như hình vẽ. Hàm số 3 23 3 3 2019y g x f x x x x đồng biến trong khoảng nào? BÀI TOÁN 4: VDC KHÔNG MẪU MỰC Câu 227: Cho hàm số f x có đạo hàm liên tục trên . Bảng biến thiên của hàm số f x như hình vẽ. Hàm số 1 2 xg x f x nghịch biến trên khoảng nào trong các khoảng sau? A. 4; 2 . B. 2;0 . C. 0;2 . D. 2;4 . Câu 228: Cho hàm số y f x có đạo hàm 21 2f x x x x với mọi .x Hỏi hàm số 2 5 4 xg x f x đồng biến trên khoảng nào trong các khoảng sau? A. ; 2 . B. 2;1 . C. 0;2 . D. 2;4 . Câu 229: Cho hàm số ( )f x có bảng xét dấu của đạo hàm như sau: Hàm số 33 ( 3) 12y f x x x nghịch biến trên khoảng nào dưới đây? A. ( ; 1). B. ( 1;0). C. (0;2). D. (2; ). Câu 230: Cho hàm số ( )f x có bảng xét dấu của đạo hàm như sau: HOÀNG TUYÊN MINH TÂM CHIỀU BIẾN THIÊN HÀM SƯU TẦM & TỔNG HỢP Trang 47 Hàm số 22 (1 ) 1y f x x x nghịch biến trên khoảng nào dưới đây? A. ( 3; 2). B. ( ; 2). C. ( ;1). D. ( 2;0). Câu 231: Cho hàm số y f x có đạo hàm liên tục trên . Đồ thị hàm số y f x như hình bên. Hàm số 2 1 2 xg x f x x nghịch biến trên khoảng nào trong các khoảng sau? A. 3;1 . B. 2;0 . C. 31; . 2 D. 1;3 . Câu 232: Cho hàm số .y f x Đồ thị hàm số y f x như hình vẽ bên và 2 2 0f f . Hỏi hàm số 2g x f x nghịch biến trên khoảng nào trong các khoảng sau? A. 31; . 2 B. 2; 1 . C. 1;1 . D. 1;2 . Câu 233: Cho đồ thị của ba hàm số , ,y f x y f x y f x như ở hình vẽ bên. Xác định xem 1 2 3, ,C C C tương ứng là đồ thị hàm số nào? A. , ,y f x y f x y f x . B. , ,y f x y f x y f x . C. , ,y f x y f x y f x . D. , ,y f x y f x y f x . Câu 234: Cho đồ thị của ba hàm số , ,y f x y f x y f x được vẽ mô tả ở hình dưới đây. Hỏi đồ thị các hàm số ,y f x y f x và y f x theo thứ tự, lần lượt tương ứng với đường cong nào? A. 3 2 1; ;C C C B. 2 1 3; ;C C C C. 2 3 1; ;C C C D. 1 3 2; ;C C C Câu 235: Cho hàm số .y f x Đồ thị hàm số y f x như hình vẽ bên. Hàm số 1 2 ... 2021y f x x x đồng biến trên khoảng nào trong các khoảng sau? A. ;1010 B. 1011; CHIỀU BIẾN THIÊN HÀM SỐ HOÀNG TUYÊN MINH TÂM Trang 48 SƯU TẦM & TỔNG HỢP C. 1011;1012 D. 1010;1011 Câu 236: Cho ba hàm số , ' , ''y f x y f x y f x có đồ thị được vẽ mô tả như ở hình vẽ bên. Hỏi rằng đồ thị của các hàm số , 'y f x y f x và ''y f x theo thứ tự, lần lượt tương ứng với đường cong nào? A. 3 2 1; ;C C C B. 2 1 3; ;C C C C. 2 3 1; ;C C C D. 1 3 2; ;C C C Câu 237: Biết , ' , ''y f x y f x y f x có đồ thị là các đồ thị có trong hình vẽ bên. Xác định xem 1 2 3, ,C C C tương ứng là đồ thị của hàm số nào? A. , ' , "f x f x f x B. ' , , "f x f x f x C. , " , 'f x f x f x D. ' , " ,f x f x f x Câu 238: Cho hàm số .y f x Đồ thị hàm số y f x như hình bên. Hàm số 2 22 3 2 2g x f x x x x đồng biến trên khoảng nào? A. 1 ; . 2 B. 1; . 2 C. ; 1 . D. 1; . Câu 239: Hàm số y f x có 2 2 0f f và y f x như hình bên. Hàm số 23g x f x nghịch biến trên khoảng nào? A. 2;2 . B. 1;2 . C. 2;5 . D. 5; . Câu 240: Cho hàm số y f x có đạo hàm liên tục trên . Đồ thị hàm số y f x như hình bên. Hàm số 22g x f x x đồng biến trên khoảng nào trong các khoảng sau đây? A. ; 2 . B. 2;2 . C. 2;4 . D. 2; . Câu 241: Cho hàm số y f x có đạo hàm liên tục trên . Đồ thị hàm số y f x như hình bên. Hỏi hàm số 22 1g x f x x đồng biến trên khoảng nào trong các khoảng sau? A. 3;1 . B. 1;3 . C. ;3 . D. 3; . HOÀNG TUYÊN MINH TÂM CHIỀU BIẾN THIÊN HÀM SƯU TẦM & TỔNG HỢP Trang 49 Câu 242: Cho hàm số y f x có đạo hàm 22 9 4f x x x x với mọi .x Hàm số 2g x f x đồng biến trên khoảng nào trong các khoảng sau? A. 2;2 . B. ; 3 . C. ; 3 0;3 . D. 3; . Câu 243: Cho hai hàm số y f x , y g x có đạo hàm trên tập số thực. Biết rằng hai hàm số y f x và y g x có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y g x . Hỏi rằng hàm số 34 2 2 h x f x g x đồng biến trên khoảng nào dưới đây? A. 315; 5 . B. 9 ; 3 4 . C. 31; 5 . D. 256; 4 . Câu 244: Cho hàm số ( )y f x liên tục trên có (0) 0f và đồ thị hàm số ( )y f x như hình vẽ bên. Hàm số 33 ( )y f x x đồng biến trên khoảng A. (2; ). B. ( ;2). C. (0;2). D. (1;3). Câu 245: Tìm tất cả các giá trị của tham số m để hàm số 22 4 6y x m x x đồng biến trên khoảng ; . A. 1 1.m B. 2 2.m C. 1m hoặc 1.m D. 2 2.m Câu 246: Có bao nhiêu số nguyên dương m để hàm số 21 2 2 1 12 3 y x x m đồng biến trên tập xác định. A. 1. B. 2. C. 3. D. 4. Câu 247: Tìm tất cả các giá trị của tham số m để hàm số 3 3 4y x mx nghịch biến trên khoảng ; 1 . A. 41 . 3 x B. 1m . C. 41 . 3 x D. Không tồn tại m. Câu 248: Có bao nhiêu giá trị nguyên của tham số 10;10m để hàm số 3 22 3 4y x mx m x đồng biến trên 0; . A. 5. B. 8. C. 19. D. 20. Câu 249: Cho hàm số g x liên tục trên đoạn 2;2 và có đồ thị như hình vẽ; hàm số f x có đạo hàm 3 3 2 8x x f x m g x . Tìm tất cả các giá trị của tham số m đề hàm số y f x nghịch biến trên đoạn 2;2 . A. 1.m B. 2.m C. .m D. 2 4m . CHIỀU BIẾN THIÊN HÀM SỐ HOÀNG TUYÊN MINH TÂM Trang 50 SƯU TẦM & TỔNG HỢP Câu 250: Cho hàm số g x liên tục trên đoạn và có bảng biến thiên như hình vẽ; hàm số f x có đạo hàm 4 27 2 5 g x x x f x m . Tìm tất cả các giá trị của tham số m đề hàm số y f x nghịch biến trên đoạn 2;2 . A. 1 . 4 m B. 7 4 m C. 1m D. 1m Câu 251: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số 2 5 3 2 21 1 10 205 3f x m x mx x m m x đồng biến trên . Tổng giá trị của tất cả các phần tử thuộc S bằng A. 3 2 . B. 2 . C. 5 2 . D. 1 2 . Câu 252: Cho hàm số y f x liên tục trên và có bảng xét dấu 'f x như hình vẽ Giá trị của tham số m để hàm số 2 2 11 1 y g x f x x mx m luôn đồng biến trên 3;0 A. 2;1m B. ;2m C. 1;0m D. 0;m Câu 253: Cho hàm số 3 21 ( , , ) 6 f x x ax bx c a b c thỏa mãn 0 1 2f f f . Tổng giá trị lớn nhất và giá trị nhỏ nhất của c để hàm số 2 2g x f f x nghịch biến trên khoảng 0;1 là A. 1. B. 1 3. . C. 3. . D. 1 3. . Câu 254: Cho hàm số f x có bảng xét dấu của đạo hàm: x 1 2 3 4 'f x 0 0 0 0 Hàm số 22 1 1y f x x x nghịch biến trên khoảng nào dưới đây? A. ;1 . B. ; 2 . C. 2;0 . D. 3; 2 . HOÀNG TUYÊN MINH TÂM CHIỀU BIẾN THIÊN HÀM SƯU TẦM & TỔNG HỢP Trang 51 Câu 255: Cho hàm số y f x có đồ thị y f x như hình vẽ bên. Hàm số 22 2 1 y f x x nghịch biến trên khoảng A. 0;2 . B. 3;4 . C. 0;1 . D. 1;2 . Câu 256: Cho f x mà đồ thị hàm số y f x như hình bên. Hàm số 21 2y f x x x đồng biến trên khoảng A. 1;2 . B. 1;0 . C. 0;1 . D. 2; 1 . Câu 257: Cho hàm số f x có bảng biến thiên như sau: Hàm số 3 23.y f x f x nghịch biến trên khoảng nào dưới đây A. 2;3 B. 1;2 C. 3;4 D. ;1 Câu 258: Cho hàm số f x có đồ thị của hàm số y f x như hình vẽ Hàm số 3 22 1 2 3 xy f x x x nghịch biến trên khoảng nào sau đây? A. 1;0 . B. 6; 3 . C. 3;6 . D. 6; . Câu 259: Cho hàm số f x có đồ thị hàm số 'y f x được cho như hình vẽ bên. Hàm số 2cosy f x x x đồng biến trên khoảng CHIỀU BIẾN THIÊN HÀM SỐ HOÀNG TUYÊN MINH TÂM Trang 52 SƯU TẦM & TỔNG HỢP A. 1;2 B. 1;0 C. 0;1 D. 2; 1 Câu 260: Cho hàm số y f x có đạo hàm liên tục trên . Đồ thì của hàm số 'y f x như hình vẽ bên. Hàm số 2 1 1 2 4g x f x x x đồng biến trên khoảng nào dưới đây? A. 12; 2 B. ; 2 C. 1; 2 D. 1;2 2 Câu 261: Cho hàm số y f x liên tục trên và có bảng biến thiên như hình vẽ. Đặt 63 1 1 S t t với t f x f x a c . Khẳng định đúng với mọi ;x b c là A. 9S . B. 9 4S . C. 3S . D. 4 3S . Câu 262: Cho hàm số f x có bảng xét dấu của đạo hàm như sau: Hàm số 22 1 1y f x x x nghịch biến trên khoảng nào dưới đây? A. ;1 . B. ; 2 . C. 2;0 . D. 3; 2 . Câu 263: Cho hàm số 3 2f x ax bx cx d ( , , ,a b c d là các hằng số thực và 0a ). Biết rằng đồ thị hai hàm số y f x và 'y f x cắt nhau tại ba điểm có điểm có hoành độ lần lượt là 3;0;4 ( tham số hình vẽ). Hàm số 4 3 23 2 2019 4 3 3 a b a c bg x x x x d c x nghịch biến trên khoảng nào dưới đây? A. 3;0 B. 3;4 C. 0; D. 0;4 HOÀNG TUYÊN MINH TÂM CHIỀU BIẾN THIÊN HÀM SƯU TẦM & TỔNG HỢP Trang 53 Câu 264: Với 3 2 1f x x ax bx và 3 2 1g x x cx dx là hai hàm đa thức bậc ba, thỏa mãn điều kiện ràng buộc 1b d , và hàm số y f g x là một hàm đồng biến trên tập xác định. Khi đó giá trị lớn nhất của 2 22 3M a c là A. 3 . B. 9 . C. 5 . D. 1.
File đính kèm:
 tai_lieu_on_thi_thpt_quoc_gia_mon_toan_chuyen_de_chieu_bien.pdf
tai_lieu_on_thi_thpt_quoc_gia_mon_toan_chuyen_de_chieu_bien.pdf

