Tái cấu hình lưới điện phân phối giảm tổn thất công suất sử dụng thuật toán runner root

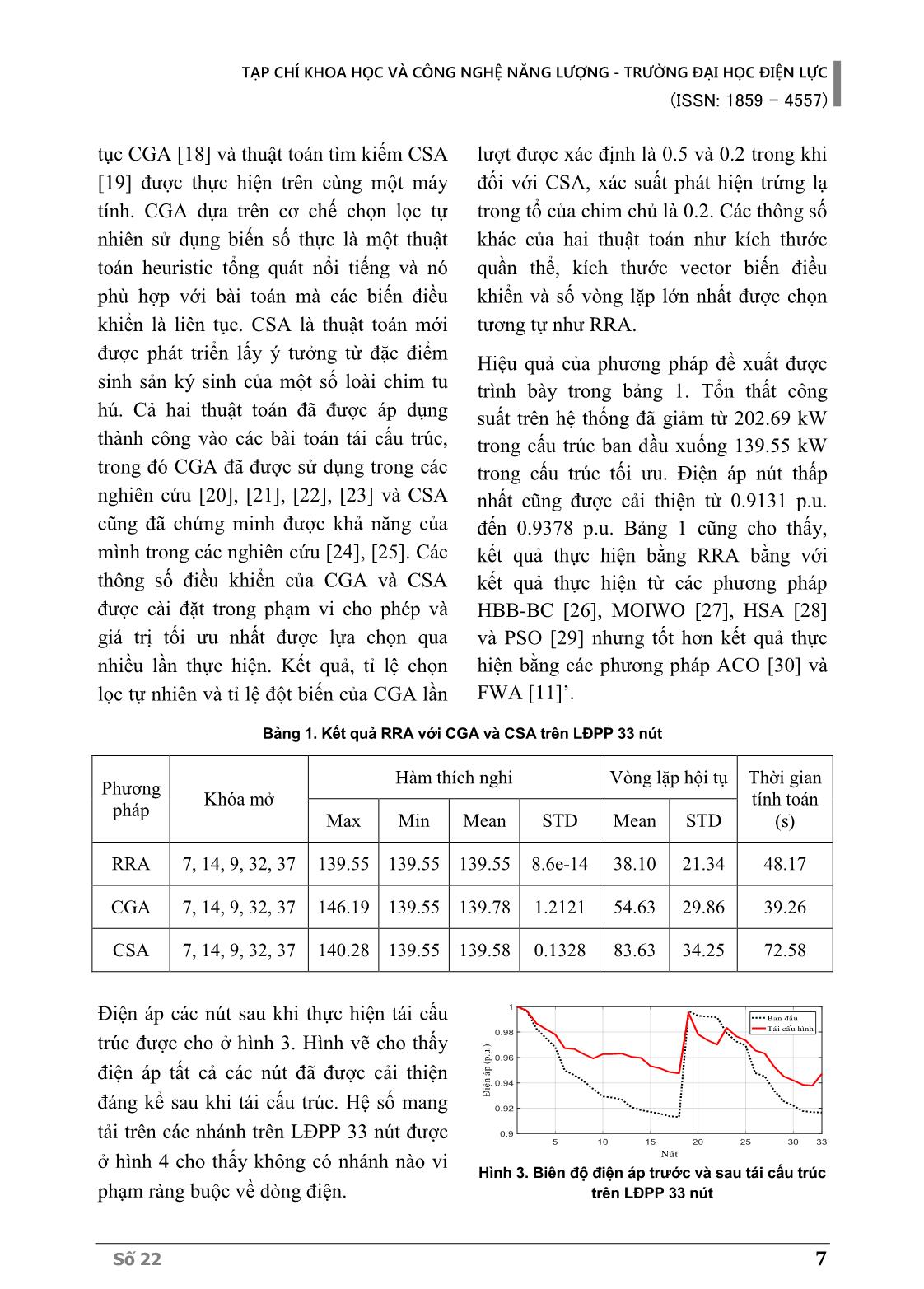
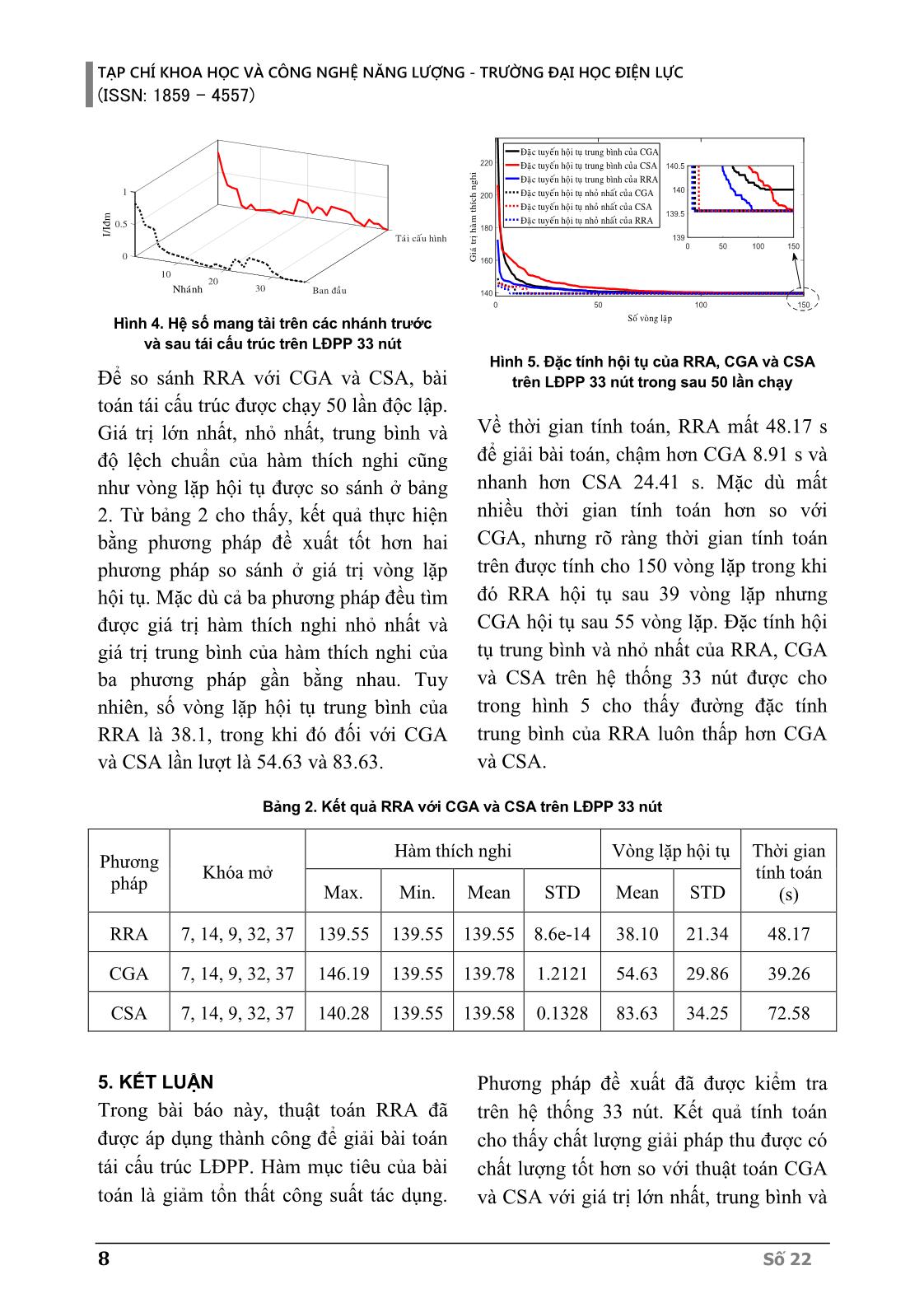
oán 
được xây dựng dưới dạng “file.m” và 
chạy từ “Command Window” của phần 
mềm MATLAB trên máy tính có cấu trúc 
Intel Core i3 M 330 @ 2.13GHz, 1 CPU, 
2 cores per CPU, Motherboard Aspire 
4740, 2GB DDR3 RAM, Hard Drive 
ST9250320AS (250GB), Windows 7 SP1 
(32-bit). Thông số của RRA sử dụng tính 
toán là số cây mẹ 𝑁 = 20; vòng lặp lớn 
nhất 𝑖𝑡𝑒𝑟𝑚𝑎𝑥 = 150; sự thay đổi tương 
đối giá trị hàm thích nghi tốt nhất trong 
hai vòng lặp 𝑡𝑜𝑙 = 0.01; số vòng lặp để 
khởi động lại thuật toán 𝑆𝑡𝑎𝑙𝑙𝑚𝑎𝑥 = 50. 
Do bởi số lượng khóa mở ban đầu trên 
lưới 33 là 5 nên kích thước của vector giải 
pháp của hệ thống được chọn là 𝑑𝑖𝑚 = 5. 
LĐPP 33 nút với 37 nhánh, 32 khóa điện 
thường đóng và 5 khóa điện thường mở 
được sử dụng để kiểm tra phương pháp đề 
nghị. Thông số đường dây và phụ tải của 
hệ thống được sử dụng trong [17] và sơ 
đồ đơn tuyến của hệ thống được mô tả 
như hình 2. Ngoài ra, tổn thất công suất 
ban đầu, điện áp nút thấp nhất và dòng 
điện định mức của các nhánh lần lượt là 
202.69 kW, 0.9131 p.u và 255 A. 
54 6 82 3 7
19
9 1211 1413 1615 1817
26 27 28 29 30 31 32 33
23 24 25
20 21 22
10
2 3 54 6 7
18
19 20
33
1 9 10 11 12 13 14
34
8
21 35
15 16 17
25
26 27 28 29 30 31 32 36
37
22
23 24
1
Hình 2. LĐPP IEEE 33 nút 
Ngoài ra, để đảm bảo sự công bằng trong 
so sánh, hai phương pháp tái cấu trúc sử 
dụng thuật toán di truyền với các biến liên 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 22 7 
tục CGA [18] và thuật toán tìm kiếm CSA 
[19] được thực hiện trên cùng một máy 
tính. CGA dựa trên cơ chế chọn lọc tự 
nhiên sử dụng biến số thực là một thuật 
toán heuristic tổng quát nổi tiếng và nó 
phù hợp với bài toán mà các biến điều 
khiển là liên tục. CSA là thuật toán mới 
được phát triển lấy ý tưởng từ đặc điểm 
sinh sản ký sinh của một số loài chim tu 
hú. Cả hai thuật toán đã được áp dụng 
thành công vào các bài toán tái cấu trúc, 
trong đó CGA đã được sử dụng trong các 
nghiên cứu [20], [21], [22], [23] và CSA 
cũng đã chứng minh được khả năng của 
mình trong các nghiên cứu [24], [25]. Các 
thông số điều khiển của CGA và CSA 
được cài đặt trong phạm vi cho phép và 
giá trị tối ưu nhất được lựa chọn qua 
nhiều lần thực hiện. Kết quả, tỉ lệ chọn 
lọc tự nhiên và tỉ lệ đột biến của CGA lần 
lượt được xác định là 0.5 và 0.2 trong khi 
đối với CSA, xác suất phát hiện trứng lạ 
trong tổ của chim chủ là 0.2. Các thông số 
khác của hai thuật toán như kích thước 
quần thể, kích thước vector biến điều 
khiển và số vòng lặp lớn nhất được chọn 
tương tự như RRA. 
Hiệu quả của phương pháp đề xuất được 
trình bày trong bảng 1. Tổn thất công 
suất trên hệ thống đã giảm từ 202.69 kW 
trong cấu trúc ban đầu xuống 139.55 kW 
trong cấu trúc tối ưu. Điện áp nút thấp 
nhất cũng được cải thiện từ 0.9131 p.u. 
đến 0.9378 p.u. Bảng 1 cũng cho thấy, 
kết quả thực hiện bằng RRA bằng với 
kết quả thực hiện từ các phương pháp 
HBB-BC [26], MOIWO [27], HSA [28] 
và PSO [29] nhưng tốt hơn kết quả thực 
hiện bằng các phương pháp ACO [30] và 
FWA [11]’. 
Bảng 1. Kết quả RRA với CGA và CSA trên LĐPP 33 nút 
Phương 
pháp 
Khóa mở 
Hàm thích nghi Vòng lặp hội tụ Thời gian 
tính toán 
(s) Max Min Mean STD Mean STD 
RRA 7, 14, 9, 32, 37 139.55 139.55 139.55 8.6e-14 38.10 21.34 48.17 
CGA 7, 14, 9, 32, 37 146.19 139.55 139.78 1.2121 54.63 29.86 39.26 
CSA 7, 14, 9, 32, 37 140.28 139.55 139.58 0.1328 83.63 34.25 72.58 
Điện áp các nút sau khi thực hiện tái cấu 
trúc được cho ở hình 3. Hình vẽ cho thấy 
điện áp tất cả các nút đã được cải thiện 
đáng kể sau khi tái cấu trúc. Hệ số mang 
tải trên các nhánh trên LĐPP 33 nút được 
ở hình 4 cho thấy không có nhánh nào vi 
phạm ràng buộc về dòng điện. 
Hình 3. Biên độ điện áp trước và sau tái cấu trúc 
trên LĐPP 33 nút 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
8 Số 22 
Hình 4. Hệ số mang tải trên các nhánh trước 
và sau tái cấu trúc trên LĐPP 33 nút 
Để so sánh RRA với CGA và CSA, bài 
toán tái cấu trúc được chạy 50 lần độc lập. 
Giá trị lớn nhất, nhỏ nhất, trung bình và 
độ lệch chuẩn của hàm thích nghi cũng 
như vòng lặp hội tụ được so sánh ở bảng 
2. Từ bảng 2 cho thấy, kết quả thực hiện 
bằng phương pháp đề xuất tốt hơn hai 
phương pháp so sánh ở giá trị vòng lặp 
hội tụ. Mặc dù cả ba phương pháp đều tìm 
được giá trị hàm thích nghi nhỏ nhất và 
giá trị trung bình của hàm thích nghi của 
ba phương pháp gần bằng nhau. Tuy 
nhiên, số vòng lặp hội tụ trung bình của 
RRA là 38.1, trong khi đó đối với CGA 
và CSA lần lượt là 54.63 và 83.63. 
Hình 5. Đặc tính hội tụ của RRA, CGA và CSA 
trên LĐPP 33 nút trong sau 50 lần chạy 
Về thời gian tính toán, RRA mất 48.17 s 
để giải bài toán, chậm hơn CGA 8.91 s và 
nhanh hơn CSA 24.41 s. Mặc dù mất 
nhiều thời gian tính toán hơn so với 
CGA, nhưng rõ ràng thời gian tính toán 
trên được tính cho 150 vòng lặp trong khi 
đó RRA hội tụ sau 39 vòng lặp nhưng 
CGA hội tụ sau 55 vòng lặp. Đặc tính hội 
tụ trung bình và nhỏ nhất của RRA, CGA 
và CSA trên hệ thống 33 nút được cho 
trong hình 5 cho thấy đường đặc tính 
trung bình của RRA luôn thấp hơn CGA 
và CSA. 
Bảng 2. Kết quả RRA với CGA và CSA trên LĐPP 33 nút 
Phương 
pháp 
Khóa mở 
Hàm thích nghi Vòng lặp hội tụ Thời gian 
tính toán 
(s) Max. Min. Mean STD Mean STD 
RRA 7, 14, 9, 32, 37 139.55 139.55 139.55 8.6e-14 38.10 21.34 48.17 
CGA 7, 14, 9, 32, 37 146.19 139.55 139.78 1.2121 54.63 29.86 39.26 
CSA 7, 14, 9, 32, 37 140.28 139.55 139.58 0.1328 83.63 34.25 72.58 
5. KẾT LUẬN 
Trong bài báo này, thuật toán RRA đã 
được áp dụng thành công để giải bài toán 
tái cấu trúc LĐPP. Hàm mục tiêu của bài 
toán là giảm tổn thất công suất tác dụng. 
Phương pháp đề xuất đã được kiểm tra 
trên hệ thống 33 nút. Kết quả tính toán 
cho thấy chất lượng giải pháp thu được có 
chất lượng tốt hơn so với thuật toán CGA 
và CSA với giá trị lớn nhất, trung bình và 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 22 9 
độ lệch chuẩn của hàm thích nghi trong 
50 lần chạy độc lập bé hơn so với CGA và 
CSA. Ngoài ra, phương pháp RRA có khả 
năng tìm được cấu trúc vận hành LĐPP 
với số vòng lặp nhỏ hơn nhiều so với 
phương pháp CGA và CSA. Vì vậy đây là 
công cụ tiềm năng và hiệu quả để giải bài 
toán tái cấu trúc LĐPP. 
TÀI LIỆU THAM KHẢO 
[1] S. Gopiya Naik, D.K. Khatod, and M.P. Sharma, “Optimal allocation of combined DG and capacitor 
for real power loss minimization in distribution networks,” International Journal of Electrical Power 
and Energy Systems, vol. 53, pp. 967–973, 2013. 
[2] A. Merlin and H. Back, “Search for a minimal loss operating spanning tree configuration in an urban 
power distribution system,” Proceeding in 5th power system computation conf (PSCC), Cambridge, 
UK, vol. 1, pp. 1–18, 1975. 
[3] S. Civanlar, J.J. Grainger, H. Yin, and S.S.H. Lee, “Distribution feeder reconfiguration for loss 
reduction,” IEEE Transactions on Power Delivery, vol. 3, no. 3, pp. 1217–1223, 1988. 
[4] D. Shirmohammadi and H.W. Hong, “Reconfiguration of electric distribution networks for resistive 
line losses reduction,” IEEE Transactions on Power Delivery, vol. 4, no. 2, pp. 1492–1498, 1989. 
[5] J.Z. Zhu, “Optimal reconfiguration of electrical distribution network using the refined genetic 
algorithm,” Electric Power Systems Research, vol. 62, no. 1, pp. 37–42, 2002. 
[6] R.T. Ganesh Vulasala, Sivanagaraju Sirigiri, “Feeder Reconfiguration for Loss Reduction in 
Unbalanced Distribution System Using Genetic Algorithm,” International Journal of Electrical and 
Electronics Engineering, vol. 3, no. 12, pp. 754–762, 2009. 
[7] P. Subburaj, K. Ramar, L. Ganesan, and P. Venkatesh, “Distribution System Reconfiguration for 
Loss Reduction using Genetic Algorithm,” Journal of Electrical Systems, vol. 2, no. 4, pp. 198–207, 
2006. 
[8] K.K. Kumar, N. Venkata, and S. Kamakshaiah, “FDR particle swarm algorithm for network 
reconfiguration of distribution systems,” Journal of Theoretical and Applied Information 
Technology, vol. 36, no. 2, pp. 174–181, 2012. 
[9] T.M. Khalil and A.V. Gorpinich, “Reconfiguration for Loss Reduction of Distribution Systems Using 
Selective Particle Swarm Optimization,” International Journal of Multidisciplinary Sciences and 
Engineering, vol. 3, no. 6, pp. 16–21, 2012. 
[10] A.Y. Abdelaziz, S.F. Mekhamer, F.M. Mohammed, and M. a L. Badr, “A Modified Particle Swarm 
Technique for Distribution Systems Reconfiguration,” The online journal on electronics and 
electrical engineering(OJEEE), vol. 1, no. 1, pp. 121–129, 2009. 
[11] A. Mohamed Imran and M. Kowsalya, “A new power system reconfiguration scheme for power loss 
minimization and voltage profile enhancement using Fireworks Algorithm,” International Journal of 
Electrical Power and Energy Systems, vol. 62, pp. 312–322, 2014. 
[12] R.S. Rao, S. Venkata, L. Narasimham, M.R. Raju, and a S. Rao, “Optimal Network Reconfiguration 
of Large-Scale Distribution System Using Harmony Search Algorithm,” IEEE Transaction on Power 
System, vol. 26, no. 3, pp. 1080–1088, 2011. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
10 Số 22 
[13] A.Y. Abdelaziz, F.M. Mohamed, S.F. Mekhamer, and M.A.L. Badr, “Distribution system 
reconfiguration using a modified Tabu Search algorithm,” Electric Power Systems Research, vol. 80, 
no. 8, pp. 943–953, 2010. 
[14] S.. Mirhoseini, S.M. Hosseini, M. Ghanbari, and M. Ahmadi, “A new improved adaptive imperialist 
competitive algorithm to solve the reconfiguration problem of distribution systems for loss 
reduction and voltage profile improvement,” International Journal of Electrical Power and Energy 
Systems, vol. 55, pp. 128–143, 2014. 
[15] A.R. Jordehi, “Optimisation of electric distribution systems: A review,” Renewable and Sustainable 
Energy Reviews, vol. 51, pp. 1088–1100, 2015. 
[16] F. Merrikh-Bayat, “The runner-root algorithm: A metaheuristic for solving unimodal and multimodal 
optimization problems inspired by runners and roots of plants in nature,” Applied Soft Computing, 
vol. 33, pp. 292–303, 2015. 
[17] M.E. Baran and F.F. Wu, “Network reconfiguration in distribution systems for loss reduction and 
load balancing,” IEEE Transactions on Power Delivery, vol. 4, no. 2. pp. 1401–1407, 1989. 
[18] R.L. Haupt and S.E. Haupt, Practical Genetic Algorithms, Second. John Wiley & Sons, Inc., 
Hoboken, New Jersey, 2004. 
[19] X.S. Yang and S. Deb, “Cuckoo search via Lévy flights,” in 2009 World Congress on Nature and 
Biologically Inspired Computing, NABIC 2009 - Proceedings, 2009, pp. 210–214. 
[20] J. Mendoza, R. López, D. Morales, E. López, P. Dessante, and R. Moraga, “Minimal loss 
reconfiguration using genetic algorithms with restricted population and addressed operators: Real 
application,” IEEE Transactions on Power Systems, vol. 21, no. 2, pp. 948–954, 2006. 
[21] N. Gupta, a. Swarnkar, K.R. Niazi, and R.C. Bansal, “Multi-objective reconfiguration of distribution 
systems using adaptive genetic algorithm in fuzzy framework,” IET Generation, Transmission & 
Distribution, vol. 4, no. 12, p. 1288, 2010. 
[22] N. Gupta, A. Swarnkar, and K.R. Niazi, “Distribution network reconfiguration for power quality and 
reliability improvement using Genetic Algorithms,” International Journal of Electrical Power & 
Energy Systems, vol. 54, pp. 664–671, 2014. 
[23] J.C. Cebrian and N. Kagan, “Reconfiguration of distribution networks to minimize loss and 
disruption costs using genetic algorithms,” Electric Power Systems Research, vol. 80, no. 1, pp. 
53–62, 2010. 
[24] T.T. Nguyen and A.V. Truong, “Distribution network reconfiguration for power loss minimization 
and voltage profile improvement using cuckoo search algorithm,” International Journal of Electrical 
Power and Energy Systems, vol. 68, pp. 233–242, 2015. 
[25] T.T. Nguyen, A.V. Truong, and T.A. Phung, “A novel method based on adaptive cuckoo search for 
optimal network reconfiguration and distributed generation allocation in distribution network,” 
International Journal of Electrical Power & Energy Systems, vol. 78, pp. 801–815, 2016. 
[26] M. Sedighizadeh, S. Ahmadi, and M. Sarvi, “An Efficient Hybrid Big Bang–Big Crunch Algorithm for 
Multi-objective Reconfiguration of Balanced and Unbalanced Distribution Systems in Fuzzy 
Framework,” Electric Power Components and Systems, vol. 41, no. 1, pp. 75–99, 2013. 
[27] D. Sudha Rani, N. Subrahmanyam, and M. Sydulu, “Multi-Objective Invasive Weed Optimization – 
An application to optimal network reconfiguration in radial distribution systems,” International 
Journal of Electrical Power & Energy Systems, vol. 73, pp. 932–942, 2015. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 22 11 
[28] R.S. Rao, K. Ravindra, K. Satish, and S.V.L. Narasimham, “Power Loss Minimization in Distribution 
System Using Network Reconfiguration in the Presence of Distributed Generation,” IEEE 
Transactions on Power Systems, vol. 28, no. 1, pp. 317–325, 2013. 
[29] A.Y. Abdelaziz, F.M. Mohammed, S.F. Mekhamer, and M.A.L. Badr, “Distribution Systems 
Reconfiguration using a modified particle swarm optimization algorithm,” Electric Power Systems 
Research, vol. 79, pp. 1521–1530, 2009. 
[30] Y.K. Wu, C.Y. Lee, L.C. Liu, and S.H. Tsai, “Study of reconfiguration for the distribution system with 
distributed generators,” IEEE Transactions on Power Delivery, vol. 25, no. 3, pp. 1678–1685, 2010. 
[31] H.D. Dehnavi and S. Esmaeili, “A new multiobjective fuzzy shuffled frog-leaping algorithm for 
optimal reconfiguration of radial distribution systems in the presence of reactive power 
compensators,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 21, no. 3, pp. 
864–881, 2013. 
Giới thiệu tác giả: 
Tác giả Nguyễn Thanh Thuận tốt nghiệp đại học năm 2008; nhận bằng Thạc sĩ 
năm 2012; nhận bằng Tiến sĩ ngành kỹ thuật điện năm 2018 tại Trường Đại học 
Sư phạm Kỹ thuật Thành phố Hồ Chí Minh. Hiện nay tác giả công tác tại Trường 
Đại học Công nghiệp Thành phố Hồ Chí Minh. 
Lĩnh vực nghiên cứu: lưới điện phân phối, lưới điện truyền tải, năng lượng tái tạo. 
Tác giả Nguyễn Tùng Linh tốt nghiệp đai học ngành hệ thống điện năm 2005, 
nhận bằng Thạc sĩ năm 2010 tại Trường Đại học Bách khoa Hà Nội; bảo vệ luận 
án Tiến sĩ ngành kỹ thuật điều khiển tự động hóa năm 2018 tại Viện Hàn lâm Khoa 
học Công nghệ Việt Nam. 
Lĩnh vực nghiên cứu: hệ thống điện, ứng dụng AI cho hệ thống điện, lưới điện 
phân phối, tự động hóa hệ thống điện, lưới điện phân phối. 
 . 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
12 Số 22 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 22 13