Study and Modeling DNA-Preconcentration Microfluidic Device

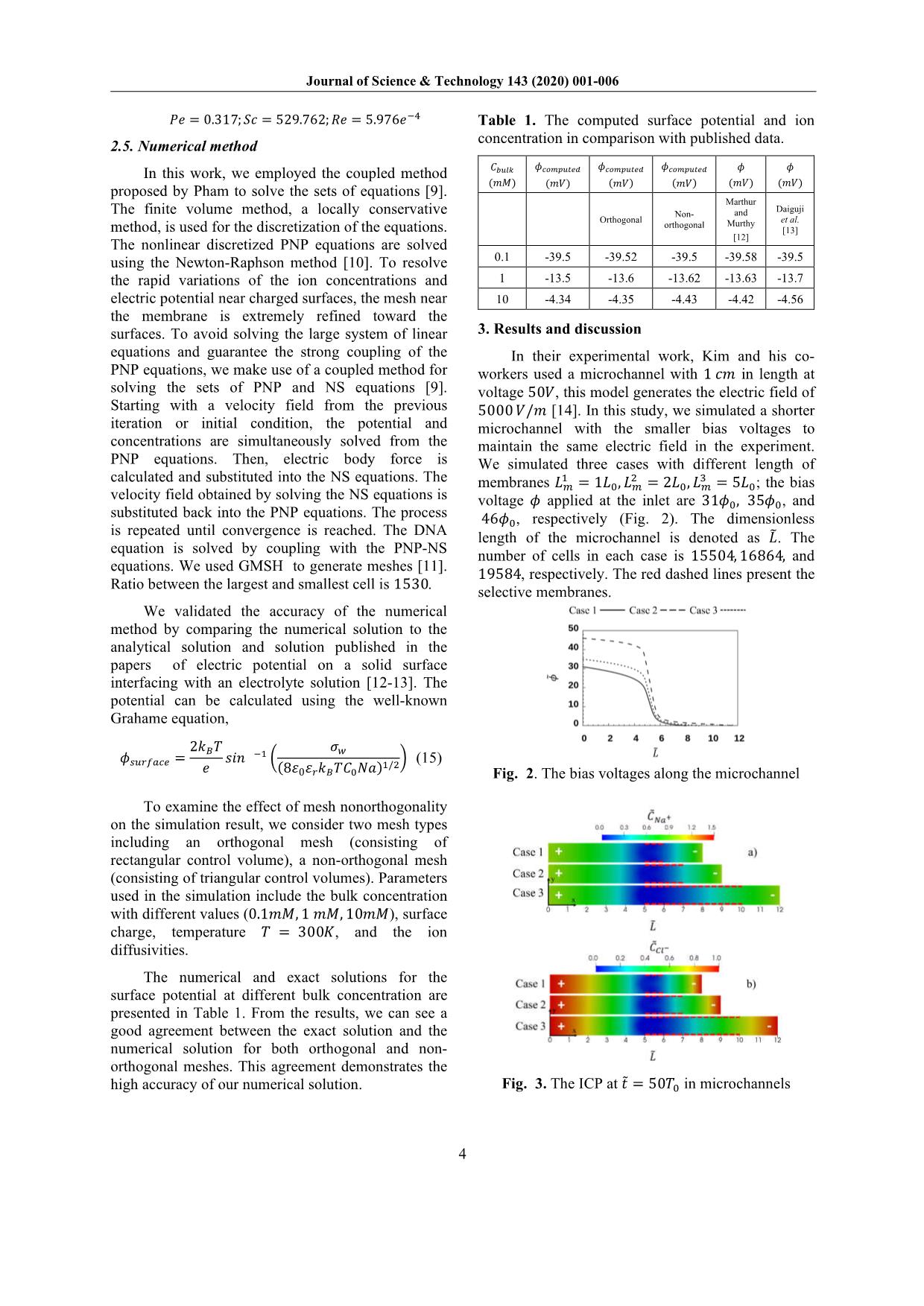
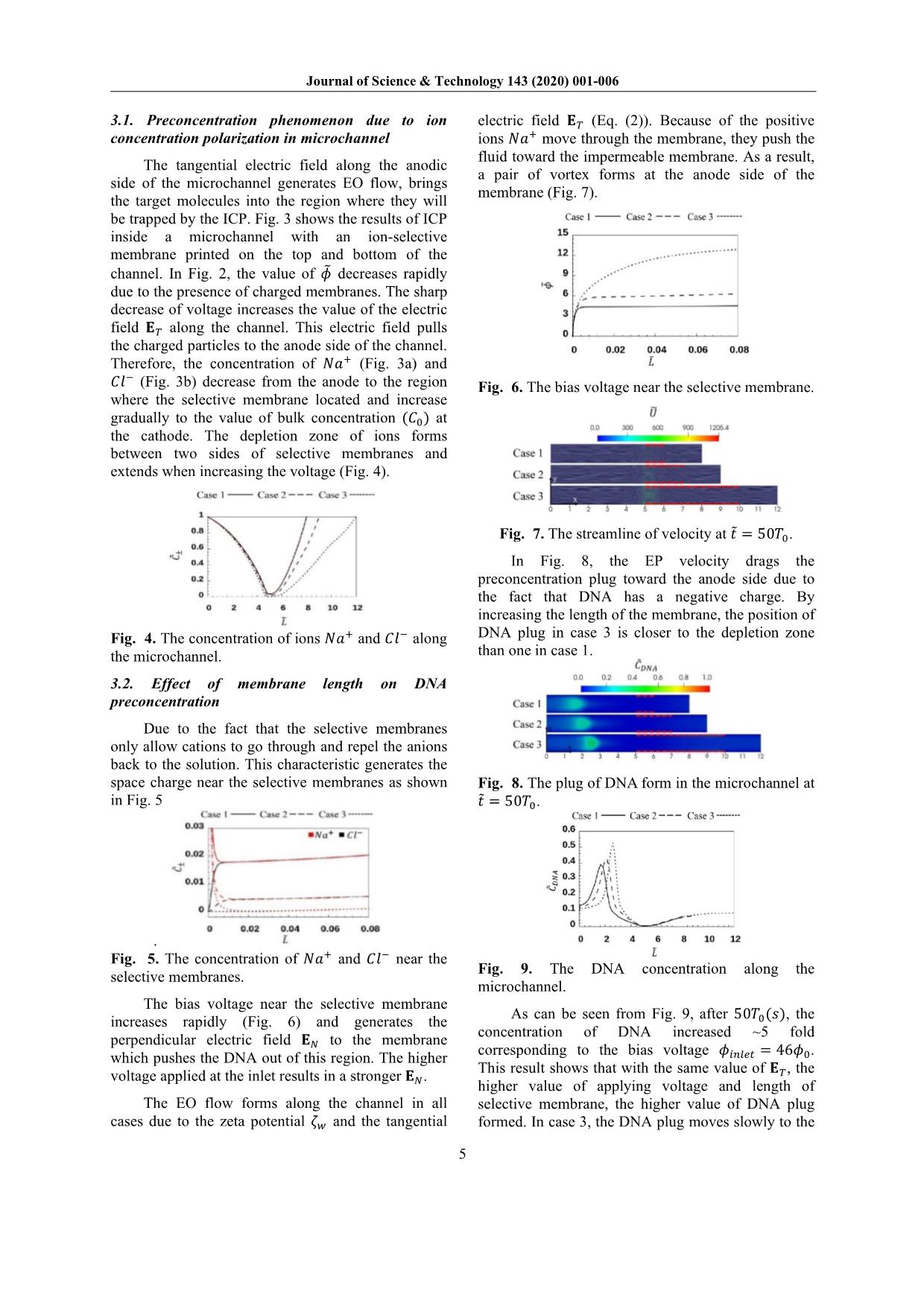
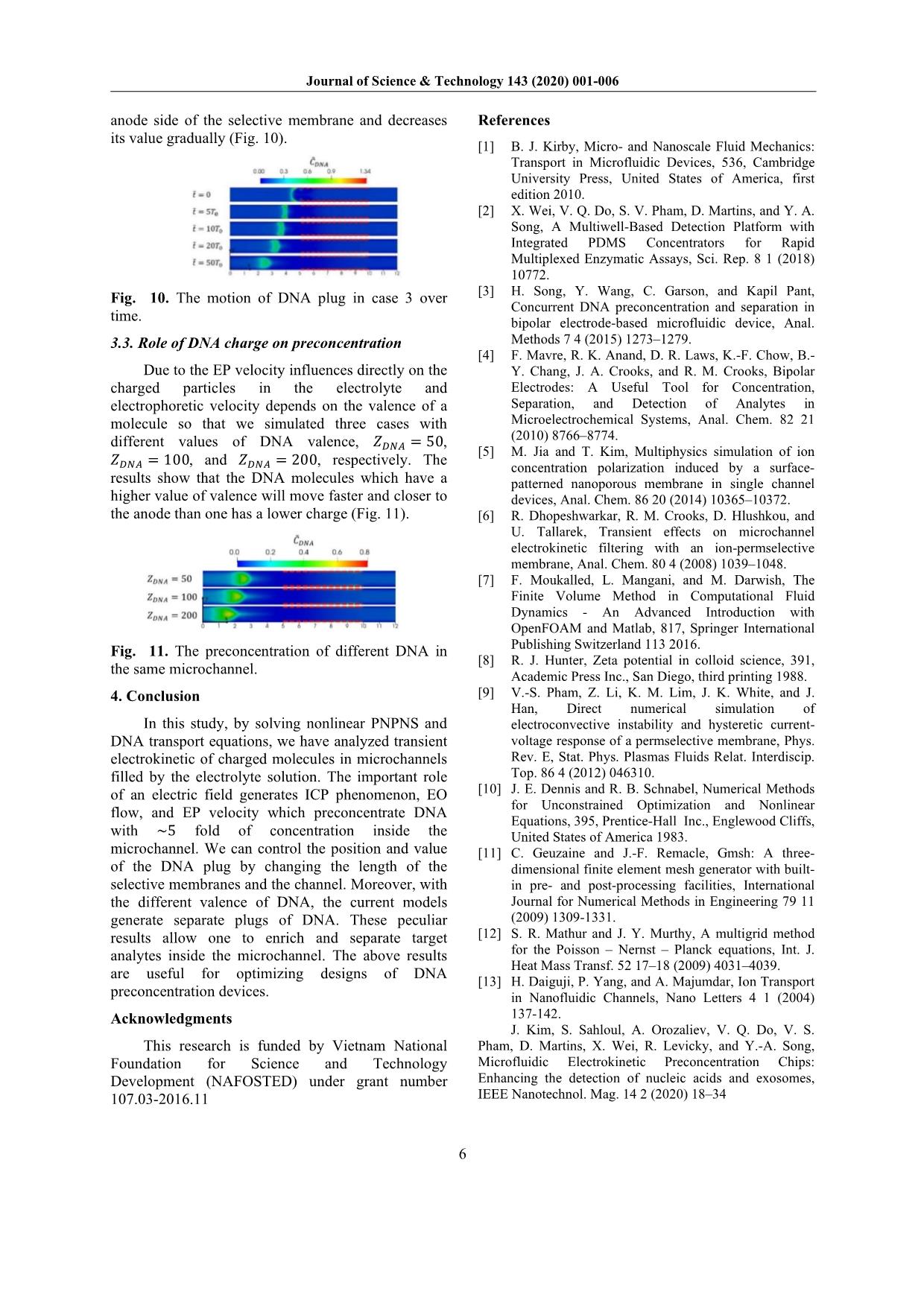
ns 
is demonstrated by Poisson Eqs. (7) and (8); and the 
fluid motion is described by the Navier-Stokes Eqs. 
(9) and (10). Dimensionless form of these equations 
is as follow: 
1

±
̃
= ∇ ± (5) 
± = ± ∇± + ± ± ∇+ ± (6) 

 ∇ ∇ =  (7) 
 =  +  (8) 
1

1


̃
= ∇ + ∇  ∇
1


∇  
(9) 
∇  = 0 (10) 
where ,̃ ± , ,  and  denote the dimensionless 
time, concentration of cations (+) and anions (-), 
electric potential, vector of fluid velocity, and 
pressure, respectively. These quantities are 
normalized by the corresponding reference values of 
time, ionic concentration, electric potential, velocity, 
and pressure, respectively as follow: 
 =



; = ; =


; 
 =


; =


(11) 
where  is the concentration scale (/
),  is 
the characteristic length scale (),  is the average 
diffusivity (/),  is the Boltzmann constant,  
is the absolute temperature (),  is the elementary 
charge (), and  = ±  is ion valence. Parameters 
± = ± ⁄ ,  =  ⁄ , and  =  ⁄ are 
dimensionless diffusion coefficient, the Debye length, 
and the space charge, respectively.  =   ⁄ , 
 =  ⁄ , and  =   ⁄ are the Péclet 
number, the Schmidt number, and the Reynolds 
number, respectively [9]. 
To investigate DNA preconcentration process in 
microchannel devices under impaction of the 
electrical force field and major ions in solution, we 
need to solve DNA transport equation: 
1


̃
= ∇ ∇
+ ∇
+  ∇ 
(12) 
where , ,  is concentration, diffusivity, 
and valence of DNA. To determine the diffusivity of 
DNA, we use empirical relations: 
 ≈ 3 × 10
/ 

1

.
 (13) 
where the contour length, , is the arc length of the 
backbone contour and can be calculated 
approximately as 
 ≈ 0.34 ×  (14) 
with  is the number of base pairs of DNA 
molecules [1]. The contour length  is the only 
molecular parameter that significantly affects DNA 
physical properties in aqueous solutions. As shown in 
Eq. (13), DNA’s diffusivity is dependent on polymer 
length, i.e., the number of base pairs. Here, we 
simulated the preconcentration of DNA which has 25, 
50, and 100 base pairs to find out the influence of 
electrophoresis on DNA transportation in the 
microchannel. 
2.4. Boundary conditions 
In order to close the Eqs. (5-10), the following 
boundary conditions were used: 
At inlet and outlet boundaries, bulk ion 
concentration boundary ± = 10; zero gradient 
boundary condition for DNA concentration; a voltage 
bias is remained between inlet and outlet to driven 
ion in the system. 
At wall boundaries, , , DNA, and  
variables have zero value, while zero gradient 
condition is applied for  and . 
At membrane surface: the concentration of 
counterion, , is fixed at the value of 15, the 
no-flux boundary condition is enforced for co-ion, 
. 
The concentration of ions and DNA was initially 
set at ±
 = 10,  = 1. Regarding the 
fluid flow, the no-slip boundary condition is enforced 
on the wall and membrane surface; the free-flow 
condition is assumed at inlet and outlet. The scales 
and dimensionless numbers, corresponding with 
above boundary conditions, are calculated below: 
 = 2.381e
(); = 10(mM); = 20 
 = 2.585e
(); = 2.66
(/); 
 = 1.183
(/); = 4.356
(); 
Journal of Science & Technology 143 (2020) 001-006 
4 
 = 0.317; = 529.762; = 5.976 
2.5. Numerical method 
In this work, we employed the coupled method 
proposed by Pham to solve the sets of equations [9]. 
The finite volume method, a locally conservative 
method, is used for the discretization of the equations. 
The nonlinear discretized PNP equations are solved 
using the Newton-Raphson method [10]. To resolve 
the rapid variations of the ion concentrations and 
electric potential near charged surfaces, the mesh near 
the membrane is extremely refined toward the 
surfaces. To avoid solving the large system of linear 
equations and guarantee the strong coupling of the 
PNP equations, we make use of a coupled method for 
solving the sets of PNP and NS equations [9]. 
Starting with a velocity field from the previous 
iteration or initial condition, the potential and 
concentrations are simultaneously solved from the 
PNP equations. Then, electric body force is 
calculated and substituted into the NS equations. The 
velocity field obtained by solving the NS equations is 
substituted back into the PNP equations. The process 
is repeated until convergence is reached. The DNA 
equation is solved by coupling with the PNP-NS 
equations. We used GMSH to generate meshes [11]. 
Ratio between the largest and smallest cell is 1530. 
We validated the accuracy of the numerical 
method by comparing the numerical solution to the 
analytical solution and solution published in the 
papers of electric potential on a solid surface 
interfacing with an electrolyte solution [12-13]. The 
potential can be calculated using the well-known 
Grahame equation, 
 =
2

  

(80)/
 (15) 
To examine the effect of mesh nonorthogonality 
on the simulation result, we consider two mesh types 
including an orthogonal mesh (consisting of 
rectangular control volume), a non-orthogonal mesh 
(consisting of triangular control volumes). Parameters 
used in the simulation include the bulk concentration 
with different values (0.1, 1 , 10), surface 
charge, temperature  = 300, and the ion 
diffusivities. 
The numerical and exact solutions for the 
surface potential at different bulk concentration are 
presented in Table 1. From the results, we can see a 
good agreement between the exact solution and the 
numerical solution for both orthogonal and non-
orthogonal meshes. This agreement demonstrates the 
high accuracy of our numerical solution. 
Table 1. The computed surface potential and ion 
concentration in comparison with published data. 
 
() 
 
() 
 
() 
 
() 
 
() 
 
() 
 Orthogonal 
Non-
orthogonal 
Marthur 
and 
Murthy 
[12] 
Daiguji 
et al. 
[13] 
0.1 -39.5 -39.52 -39.5 -39.58 -39.5 
1 -13.5 -13.6 -13.62 -13.63 -13.7 
10 -4.34 -4.35 -4.43 -4.42 -4.56 
3. Results and discussion 
In their experimental work, Kim and his co-
workers used a microchannel with 1  in length at 
voltage 50, this model generates the electric field of 
5000 / [14]. In this study, we simulated a shorter 
microchannel with the smaller bias voltages to 
maintain the same electric field in the experiment. 
We simulated three cases with different length of 
membranes 
 = 1, 
 = 2, 
 = 5; the bias 
voltage  applied at the inlet are 31, 35, and 
 46, respectively (Fig. 2). The dimensionless 
length of the microchannel is denoted as . The 
number of cells in each case is 15504, 16864, and 
19584, respectively. The red dashed lines present the 
selective membranes. 
Fig. 2. The bias voltages along the microchannel 
Fig. 3. The ICP at  =̃ 50 in microchannels 
Journal of Science & Technology 143 (2020) 001-006 
5 
3.1. Preconcentration phenomenon due to ion 
concentration polarization in microchannel 
The tangential electric field along the anodic 
side of the microchannel generates EO flow, brings 
the target molecules into the region where they will 
be trapped by the ICP. Fig. 3 shows the results of ICP 
inside a microchannel with an ion-selective 
membrane printed on the top and bottom of the 
channel. In Fig. 2, the value of  decreases rapidly 
due to the presence of charged membranes. The sharp 
decrease of voltage increases the value of the electric 
field  along the channel. This electric field pulls 
the charged particles to the anode side of the channel. 
Therefore, the concentration of  (Fig. 3a) and 
 (Fig. 3b) decrease from the anode to the region 
where the selective membrane located and increase 
gradually to the value of bulk concentration () at 
the cathode. The depletion zone of ions forms 
between two sides of selective membranes and 
extends when increasing the voltage (Fig. 4). 
Fig. 4. The concentration of ions  and  along 
the microchannel. 
3.2. Effect of membrane length on DNA 
preconcentration 
Due to the fact that the selective membranes 
only allow cations to go through and repel the anions 
back to the solution. This characteristic generates the 
space charge near the selective membranes as shown 
in Fig. 5 
. 
Fig. 5. The concentration of  and  near the 
selective membranes. 
The bias voltage near the selective membrane 
increases rapidly (Fig. 6) and generates the 
perpendicular electric field  to the membrane 
which pushes the DNA out of this region. The higher 
voltage applied at the inlet results in a stronger . 
The EO flow forms along the channel in all 
cases due to the zeta potential  and the tangential 
electric field  (Eq. (2)). Because of the positive 
ions  move through the membrane, they push the 
fluid toward the impermeable membrane. As a result, 
a pair of vortex forms at the anode side of the 
membrane (Fig. 7). 
Fig. 6. The bias voltage near the selective membrane. 
Fig. 7. The streamline of velocity at  =̃ 50. 
In Fig. 8, the EP velocity drags the 
preconcentration plug toward the anode side due to 
the fact that DNA has a negative charge. By 
increasing the length of the membrane, the position of 
DNA plug in case 3 is closer to the depletion zone 
than one in case 1. 
Fig. 8. The plug of DNA form in the microchannel at 
 =̃ 50. 
Fig. 9. The DNA concentration along the 
microchannel. 
As can be seen from Fig. 9, after 50(), the 
concentration of DNA increased ~5 fold 
corresponding to the bias voltage  = 46. 
This result shows that with the same value of , the 
higher value of applying voltage and length of 
selective membrane, the higher value of DNA plug 
formed. In case 3, the DNA plug moves slowly to the 
Journal of Science & Technology 143 (2020) 001-006 
6 
anode side of the selective membrane and decreases 
its value gradually (Fig. 10). 
Fig. 10. The motion of DNA plug in case 3 over 
time. 
3.3. Role of DNA charge on preconcentration 
Due to the EP velocity influences directly on the 
charged particles in the electrolyte and 
electrophoretic velocity depends on the valence of a 
molecule so that we simulated three cases with 
different values of DNA valence,  = 50, 
 = 100, and  = 200, respectively. The 
results show that the DNA molecules which have a 
higher value of valence will move faster and closer to 
the anode than one has a lower charge (Fig. 11). 
Fig. 11. The preconcentration of different DNA in 
the same microchannel. 
4. Conclusion 
In this study, by solving nonlinear PNPNS and 
DNA transport equations, we have analyzed transient 
electrokinetic of charged molecules in microchannels 
filled by the electrolyte solution. The important role 
of an electric field generates ICP phenomenon, EO 
flow, and EP velocity which preconcentrate DNA 
with ~5 fold of concentration inside the 
microchannel. We can control the position and value 
of the DNA plug by changing the length of the 
selective membranes and the channel. Moreover, with 
the different valence of DNA, the current models 
generate separate plugs of DNA. These peculiar 
results allow one to enrich and separate target 
analytes inside the microchannel. The above results 
are useful for optimizing designs of DNA 
preconcentration devices. 
Acknowledgments 
This research is funded by Vietnam National 
Foundation for Science and Technology 
Development (NAFOSTED) under grant number 
107.03-2016.11 
References 
[1] B. J. Kirby, Micro- and Nanoscale Fluid Mechanics: 
Transport in Microfluidic Devices, 536, Cambridge 
University Press, United States of America, first 
edition 2010. 
[2] X. Wei, V. Q. Do, S. V. Pham, D. Martins, and Y. A. 
Song, A Multiwell-Based Detection Platform with 
Integrated PDMS Concentrators for Rapid 
Multiplexed Enzymatic Assays, Sci. Rep. 8 1 (2018) 
10772. 
[3] H. Song, Y. Wang, C. Garson, and Kapil Pant, 
Concurrent DNA preconcentration and separation in 
bipolar electrode-based microfluidic device, Anal. 
Methods 7 4 (2015) 1273–1279. 
[4] F. Mavre, R. K. Anand, D. R. Laws, K.-F. Chow, B.-
Y. Chang, J. A. Crooks, and R. M. Crooks, Bipolar 
Electrodes: A Useful Tool for Concentration, 
Separation, and Detection of Analytes in 
Microelectrochemical Systems, Anal. Chem. 82 21 
(2010) 8766–8774. 
[5] M. Jia and T. Kim, Multiphysics simulation of ion 
concentration polarization induced by a surface-
patterned nanoporous membrane in single channel 
devices, Anal. Chem. 86 20 (2014) 10365–10372. 
[6] R. Dhopeshwarkar, R. M. Crooks, D. Hlushkou, and 
U. Tallarek, Transient effects on microchannel 
electrokinetic filtering with an ion-permselective 
membrane, Anal. Chem. 80 4 (2008) 1039–1048. 
[7] F. Moukalled, L. Mangani, and M. Darwish, The 
Finite Volume Method in Computational Fluid 
Dynamics - An Advanced Introduction with 
OpenFOAM and Matlab, 817, Springer International 
Publishing Switzerland 113 2016. 
[8] R. J. Hunter, Zeta potential in colloid science, 391, 
Academic Press Inc., San Diego, third printing 1988. 
[9] V.-S. Pham, Z. Li, K. M. Lim, J. K. White, and J. 
Han, Direct numerical simulation of 
electroconvective instability and hysteretic current-
voltage response of a permselective membrane, Phys. 
Rev. E, Stat. Phys. Plasmas Fluids Relat. Interdiscip. 
Top. 86 4 (2012) 046310. 
[10] J. E. Dennis and R. B. Schnabel, Numerical Methods 
for Unconstrained Optimization and Nonlinear 
Equations, 395, Prentice-Hall Inc., Englewood Cliffs, 
United States of America 1983. 
[11] C. Geuzaine and J.-F. Remacle, Gmsh: A three-
dimensional finite element mesh generator with built-
in pre- and post-processing facilities, International 
Journal for Numerical Methods in Engineering 79 11 
(2009) 1309-1331. 
[12] S. R. Mathur and J. Y. Murthy, A multigrid method 
for the Poisson – Nernst – Planck equations, Int. J. 
Heat Mass Transf. 52 17–18 (2009) 4031–4039. 
[13] H. Daiguji, P. Yang, and A. Majumdar, Ion Transport 
in Nanofluidic Channels, Nano Letters 4 1 (2004) 
137-142. 
J. Kim, S. Sahloul, A. Orozaliev, V. Q. Do, V. S. 
Pham, D. Martins, X. Wei, R. Levicky, and Y.-A. Song, 
Microfluidic Electrokinetic Preconcentration Chips: 
Enhancing the detection of nucleic acids and exosomes, 
IEEE Nanotechnol. Mag. 14 2 (2020) 18–34