Some results on new statistical randomness tests based on length of runs

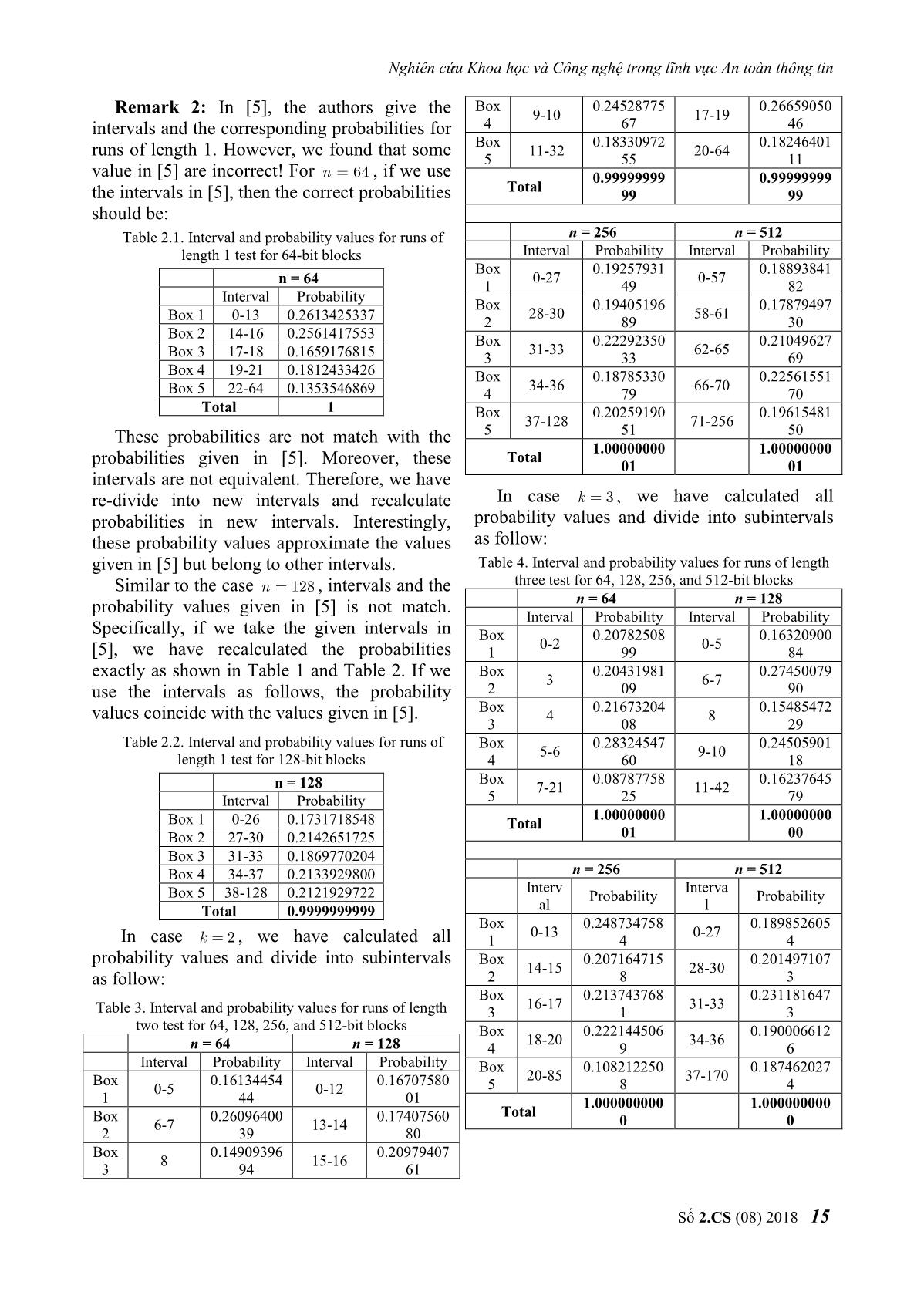
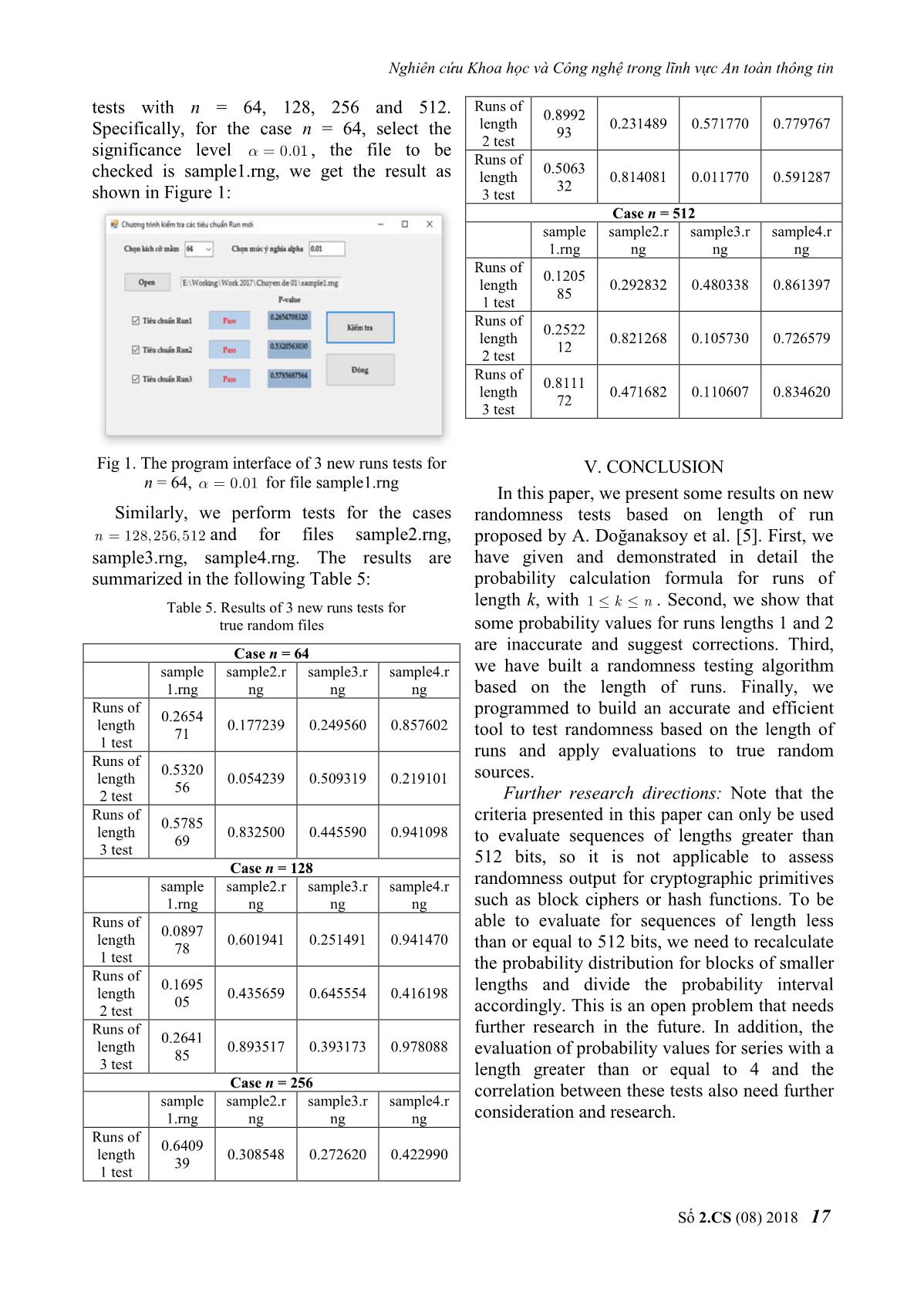
y  y 1 1k 1 
 1 2 r l l ... l 
 1 2 k ... .
 l l l 
 n l2 l ... kl k 1 r l l ... l 1 2 k 
 1 2k 1 2 k 
 It implies the probabilities 
 n k 1 r kl1 k 1 l 2 ... lk .
 N l
 k k 
 Pr rk l k . 
 2n
 We use the Algorithm 1 in order to evaluate 
 the probabilities Pr rk l k . 
 Số 2.CS (08) 2018 13 
Journal of Science and Technology on Information Security 
 Then, we get Table 1 for probability 
 Algorithm 1: Evaluate Pr rk l k for 
 subintervals. 
 l 0,1, , n / k 
 k 
 Table 1. Interval and probability values for runs of length 
 l0, , l  0, l  0, r  1, N l  0, 
 k2 1 k k one test for 128-bit blocks 
while l n/ k do 
 k Interval Probability 
  Box 1 0-27 0.2191945278 
 Box 2 28-31 0.2304573984 
 while l n / 2 do 
 2 Box 3 32-34 0.1843489091 
 while l n do Box 4 35-38 0.1945435197 
 1 Box 5 39-128 0.1714556450 
 while r n do Total 1 
 1
 N l N l Remark 1: In the Table 1, we have use the 
 k k k k n 1
 2 intervals given in [5], however the calculated 
 n/ k 1 
 n n n kr k 1 l ... l 1 
 1k 1 probabilities of Box 4 and Box 5 are not match 
   
 r l l ... l 1 
 lk 1 0 l 1 0 r 1 1 2 k with the probabilities given in [5]. After 
 r r l r l ... l retesting, we find that the authors in [5] give 
 1 1k 1 
 ... correct intervals but wrong probabilities. The 
 l l l 
 1 2 k correct probabilities are as in Table 1. 
 r r 1 Moreover, the probabilities given in [5] are 
 end while belong to the intervals 35-40, and 41-128, 
 l1 l 1 1 that can not belong to the intervals 35-38 
 end while and 39-128. 
 l l 1 Similarly, we can calculate probabilitiy 
 2 2 intervals for sequences with different lengths. 
 end while 
 The subinterval probabilities for runs of length 
 1 can be seen in Table 2. 
 lk l k 1 
 Table 2. Interval and probability values for runs of length 
end while one test for 64, 128, 256, and 512-bit blocks 
 N
return k n = 64 n = 128 
 Interva
 Computational Complexity: Let the Probability Interval Probability 
 l 
complexity of computing N l be  k then 
 k k Box 0.19008234 0.21919452
 0-12 0-27 
the complexity of probability searching 1 44 78 
 Box 0.23887746 0.23045739
algorithm for runs of length k is about 13-15 28-31 
 2 37 84 
  nk 1 k
 . Box 0.17456037 0.18434890
 16-17 32-34 
After evaluating all probability values, we 3 41 91 
 Box 0.21147040 0.19454351
divide these into 5 subintervals as in [5]. 18-20 35-38 
 4 14 97 
 Case k 1 . Box 0.18500941 0.17145564
 21-64 39-128 
 Choose n 128 , we have calculated all 5 64 50 
probability values and divide into subintervals Total 1 1 
as follow n = 256 n = 512 
 Interva
 27 31 Probability Interval Probability 
 Box1 Pr r l , Box 2 Pr r l , l 
 1 1 1  1 1 1 
 l 0 l 28 Box 0.18725584 0.19356638
 1 1 0-56 0-117 
 34 38 1 09 36 
 Box3 Pr r l , Box 4 Pr r l , 
 1 1 1  1 1 1 Box 0.18928091 0.21863011
 l1 31 l 1 35 57-61 118-125 
 128 2 85 42 
 Box5 Pr r l . Box 0.21985945 0.21707667
  1 1 1 62-66 126-132 
 l1 39 3 18 90 
 Box 0.21877592 0.19951554
 67-72 133-140 
 4 27 92 
 Box 0.18482786 0.17121127
 73-256 141-512 
 5 61 40 
 Total 1 1 
14 Số 2.CS (08) 2018 
 Nghiên cứu Khoa học và Công nghệ trong lĩnh vực An toàn thông tin 
 Box 0.24528775 0.26659050
 Remark 2: In [5], the authors give the 9-10 17-19 
intervals and the corresponding probabilities for 4 67 46 
 Box 0.18330972 0.18246401
runs of length 1. However, we found that some 11-32 20-64 
 5 55 11 
value in [5] are incorrect! For n 64 , if we use 0.99999999 0.99999999
 Total 
the intervals in [5], then the correct probabilities 99 99 
should be: 
 Table 2.1. Interval and probability values for runs of n = 256 n = 512 
 length 1 test for 64-bit blocks Interval Probability Interval Probability 
 Box 0.19257931 0.18893841
 n = 64 0-27 0-57 
 1 49 82 
 Interval Probability 
 Box 0.19405196 0.17879497
 28-30 58-61 
 Box 1 0-13 0.2613425337 2 89 30 
 Box 2 14-16 0.2561417553 Box 0.22292350 0.21049627
 31-33 62-65 
 Box 3 17-18 0.1659176815 3 33 69 
 Box 4 19-21 0.1812433426 Box 0.18785330 0.22561551
 34-36 66-70 
 Box 5 22-64 0.1353546869 4 79 70 
 Total 1 Box 0.20259190 0.19615481
 37-128 71-256 
 These probabilities are not match with the 5 51 50 
 1.00000000 1.00000000
 Total 
probabilities given in [5]. Moreover, these 01 01 
intervals are not equivalent. Therefore, we have 
re-divide into new intervals and recalculate In case k 3 , we have calculated all 
probabilities in new intervals. Interestingly, probability values and divide into subintervals 
these probability values approximate the values as follow: 
given in [5] but belong to other intervals. Table 4. Interval and probability values for runs of length 
 Similar to the case n 128 , intervals and the three test for 64, 128, 256, and 512-bit blocks 
probability values given in [5] is not match. n = 64 n = 128 
 Interval Probability Interval Probability 
Specifically, if we take the given intervals in Box 0.20782508 0.16320900
 0-2 0-5 
[5], we have recalculated the probabilities 1 99 84 
exactly as shown in Table 1 and Table 2. If we Box 0.20431981 0.27450079
 3 6-7 
use the intervals as follows, the probability 2 09 90 
 Box 0.21673204 0.15485472
values coincide with the values given in [5]. 4 8 
 3 08 29 
 Table 2.2. Interval and probability values for runs of Box 0.28324547 0.24505901
 5-6 9-10 
 length 1 test for 128-bit blocks 4 60 18 
 Box 0.08787758 0.16237645
 n = 128 7-21 11-42 
 Interval Probability 5 25 79 
 1.00000000 1.00000000
 Box 1 0-26 0.1731718548 Total 
 Box 2 27-30 0.2142651725 01 00 
 Box 3 31-33 0.1869770204 
 Box 4 34-37 0.2133929800 n = 256 n = 512 
 Interv Interva
 Box 5 38-128 0.2121929722 Probability Probability 
 Total 0.9999999999 al l 
 Box 0.248734758 0.189852605
 0-13 0-27 
 In case k 2 , we have calculated all 1 4 4 
probability values and divide into subintervals Box 0.207164715 0.201497107
 14-15 28-30 
as follow: 2 8 3 
 Box 0.213743768 0.231181647
 16-17 31-33 
 Table 3. Interval and probability values for runs of length 3 1 3 
 two test for 64, 128, 256, and 512-bit blocks Box 0.222144506 0.190006612
 18-20 34-36 
 n = 64 n = 128 4 9 6 
 Interval Probability Interval Probability Box 0.108212250 0.187462027
Box 0.16134454 0.16707580 20-85 37-170 
 0-5 0-12 5 8 4 
 1 44 01 1.000000000 1.000000000
Box 0.26096400 0.17407560 Total 
 6-7 13-14 0 0 
 2 39 80 
Box 0.14909396 0.20979407 
 8 15-16 
 3 94 61 
 Số 2.CS (08) 2018 15 
Journal of Science and Technology on Information Security 
 Remark 3: In the case of n 512 we used Also we use a variation of S , denoted by 
Magma software to divide the intervals and S of length n 1 by adding 1’s at the 
calculate the probability values because it takes beginning the sequence S . The variation of 
quite a long time to run in C ++ language. The derivative is an important part of new defned 
calculation time on Magma for this case is run tests, since the number of runs of different 
about 5000 seconds. length is determined by this sequence. 
 S s,,, s s
 C. Tests Descriptions Let 0 1n 1 be a binary sequence 
 and derivative of S is S s,,, s s . 
 After calculating the probabilities, we begin 0 1n 1
to build a new test based on the number of runs Then, S s0,,, s 1  sn is defined as 
of length k. Specifically, to test a sequence of follows 
N n m bits, where n is the block size we s if i 1,2, , n ,
 i 1
 s 
choose. Or we consider m outputs of a i 1 if i 0.
cryptographic primitive (a block cipher or a 
hash function) that have output block size is n- It is easy to prove that the total runs number 
bit. First, we'll count the number of runs of of a sequence is the weight of the derivative of 
length k of each sequence in m blocks, and that sequence, and the runs number with the 
increases the count value of the corresponding length k in a given sequence S is the number of 
sub-interval to 1. After calculating, we record samples 10  01 overlaps in S . 
the counting values of each sub-interval, k 1 
denoted by FFF,,, respectively. We use the Algorithm 2 presents the pseudocode of the 
 1 2 5 test based on the number of runs of length k: 
approach as in [8], using χ2 test to evaluate the 
 Algorithm 2: Test based on the number of 
randomness of the sequence. 
 S,,,,,,, S S L l1 l 2  l m
Consider: runs of length k 1 2 m k k k k  
 2
 5 S s ,,, s  s 
 F m Pr i i,0 i ,1 i , n
 2 i i
  , i
 i 1 m Pri i0, lk  0 
 Lastly p-value is calculated according to the while j n k do 
given values: 
 5 1 2 temp s 2k s 2 k 1 s 2 k 2  s 2 0
 i, j i , j 1 i , j 2 i , j k
 p value igamc , . 
 k
 2 2 if temp 2 1 then 
 By comparing the produced p-value with the i i
 lk l k 1 
level of significance , we can conclude about 
 end if 
the randomness of the input sequence. 
 i i 1 
Note that for 2 test, we require m Pr 5 
 i end while 
therefore for Pr 0.2 we need m 25 . Thus, 2 
 i Applying χ test for Lk 
the new tests can be applied for short sequences return p-value. 
of length N n m bit for m 25 . 
In addition, counting the total runs numbers and IV. SOME EXPERIMENTAL RESULTS 
runs numbers with length k of a sequence by We have developed a randomness test 
definition is difficult. Therefore, we use the program using tests based on runs of lengths 1, 
concept of “derivative” of a sequence. 2 and 3. The program interface is shown in 
 Definition 1 (Remark 11, [5]) (derivative of Figure 1. Specifically, we have tested 4 files 
 true random: sample1.rng, sample2.rng, 
a sequence) Let S s0,,, s 1 sn 1 be a binary 
sequence of length n, the derivative of S, sample3.rng, sample4.rng (these true random 
 files are actually 32 KB in size, that is, bits of 
denoted by S s,,, s s is defined as 
 0 1n 1 N 32 1024 8 length, downloaded at 
follows  with 
 s s if i 0,1, , n 2,
 i i 1 the following cases n = 64, 128, 256 and 512. 
 s 
 i 1 if i n 1.
 The results of all 4 files have passed 3 new runs 
16 Số 2.CS (08) 2018 
 Nghiên cứu Khoa học và Công nghệ trong lĩnh vực An toàn thông tin 
 Runs of 
tests with n = 64, 128, 256 and 512. 0.8992
 length 0.231489 0.571770 0.779767 
Specifically, for the case n = 64, select the 93 
 2 test 
significance level 0.01 , the file to be 
 Runs of 
 0.5063
checked is sample1.rng, we get the result as length 0.814081 0.011770 0.591287 
 32 
shown in Figure 1: 3 test 
 Case n = 512 
 sample sample2.r sample3.r sample4.r
 1.rng ng ng ng 
 Runs of 
 0.1205
 length 0.292832 0.480338 0.861397 
 85 
 1 test 
 Runs of 
 0.2522
 length 0.821268 0.105730 0.726579 
 12 
 2 test 
 Runs of 
 0.8111
 length 0.471682 0.110607 0.834620 
 72 
 3 test 
 Fig 1. The program interface of 3 new runs tests for V. CONCLUSION 
 n = 64, 0.01 for file sample1.rng 
 In this paper, we present some results on new 
 Similarly, we perform tests for the cases randomness tests based on length of run 
n 128,256,512 and for files sample2.rng, proposed by A. Doğanaksoy et al. [5]. First, we 
sample3.rng, sample4.rng. The results are have given and demonstrated in detail the 
summarized in the following Table 5: probability calculation formula for runs of 
 Table 5. Results of 3 new runs tests for length k, with 1 k n . Second, we show that 
 true random files some probability values for runs lengths 1 and 2 
 are inaccurate and suggest corrections. Third, 
 Case n = 64 
 sample sample2.r sample3.r sample4.r we have built a randomness testing algorithm 
 1.rng ng ng ng based on the length of runs. Finally, we 
Runs of 
 0.2654 programmed to build an accurate and efficient 
 length 0.177239 0.249560 0.857602 
 71 tool to test randomness based on the length of 
 1 test runs and apply evaluations to true random 
Runs of 
 0.5320
 length 0.054239 0.509319 0.219101 sources. 
 56 
 2 test Further research directions: Note that the 
Runs of 
 0.5785 criteria presented in this paper can only be used 
 length 0.832500 0.445590 0.941098 
 69 to evaluate sequences of lengths greater than 
 3 test 512 bits, so it is not applicable to assess 
 Case n = 128 
 sample sample2.r sample3.r sample4.r randomness output for cryptographic primitives 
 1.rng ng ng ng such as block ciphers or hash functions. To be 
Runs of able to evaluate for sequences of length less 
 0.0897
 length 0.601941 0.251491 0.941470 
 78 than or equal to 512 bits, we need to recalculate 
 1 test the probability distribution for blocks of smaller 
Runs of 
 0.1695
 length 0.435659 0.645554 0.416198 lengths and divide the probability interval 
 05 
 2 test accordingly. This is an open problem that needs 
Runs of further research in the future. In addition, the 
 0.2641
 length 0.893517 0.393173 0.978088 
 85 evaluation of probability values for series with a 
 3 test length greater than or equal to 4 and the 
 Case n = 256 correlation between these tests also need further 
 sample sample2.r sample3.r sample4.r
 1.rng ng ng ng consideration and research. 
Runs of 
 0.6409
 length 0.308548 0.272620 0.422990 
 39 
 1 test 
 Số 2.CS (08) 2018 17 
Journal of Science and Technology on Information Security 
 REFERENCES ABOUT THE AUTHOR 
 B.S. Linh Hoang Dinh 
[1]. M. D. MacLaren, “The art of computer Workplace: Institute of 
 programming. Volume 2: Seminumerical Cryptography Science and 
 algorithms (Donald E. Knuth)”, SIAM Review Technology. 
 12, pp. 306-308, 1970. 
 Email: linhhd@bcy.gov.vn 
[2]. G. Marsaglia, “The marsaglia random number 
 cdrom including the diehard battery of tests of The education process: has received 
 randomness, 1995”. URL  stat. fsu. a mathematical bachelor degree in 
 edu/pub/diehard, 2008. Ha Noi University of Science, in 
 2014. 
[3]. W. Caelli, “Crypt x package documentation”. 
 Information Security Research Centre and Research today: symmetric cryptography algorithm. 
 School of Mathematics, Queensland University 
 of Technology, 1992. 
[4]. A. Rukhin, J. Soto, J. Nechvatal, E. Barker, S. 
 Leigh, M. Levenson, D. Banks, A. Heckert, J. 
 Dray, S. Vo, “Statistical test suite for random 
 and pseudorandom number generators for 
 cryptographic applications, NIST special 
 publication”, 2010. 
[5]. A. Doğanaksoy, F. Sulak, M. Uğuz, O. Şeker, Z. 
 Akcengiz, “New statistical randomness tests 
 based on length of runs”. Mathematical 
 Problems in Engineering, 2015. 
[6]. S. W. Golomb, “Shift register sequences”. 
 Aegean Park Press, 1982. 
[7]. P. L'Ecuyer, R. Simard, “TestU01: AC library 
 for empirical testing of random number 
 generators”. ACM Transactions on 
 Mathematical Software (TOMS) 33, 22, 2007. 
[8]. F. Sulak, A. Doğanaksoy, B. Ege, O. Koçak, 
 “Evaluation of randomness test results for short 
 sequences”, in International Conference on 
 Sequences and Their Applications. Springer, pp. 
 309-319, 2010. 
18 Số 2.CS (08) 2018