PR Current Controllers for Harmonics Generators to Test an Inductive Current Transformer

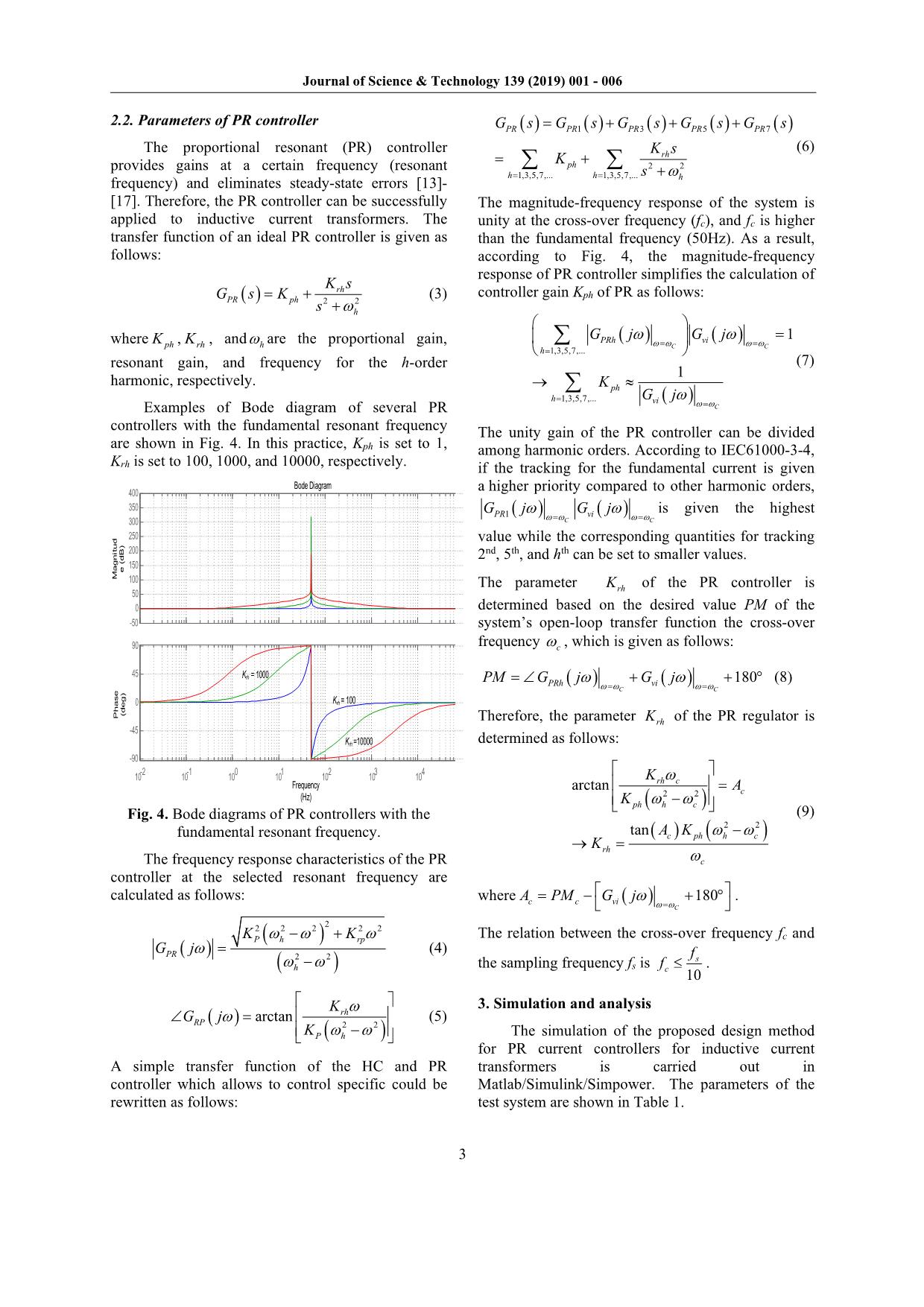
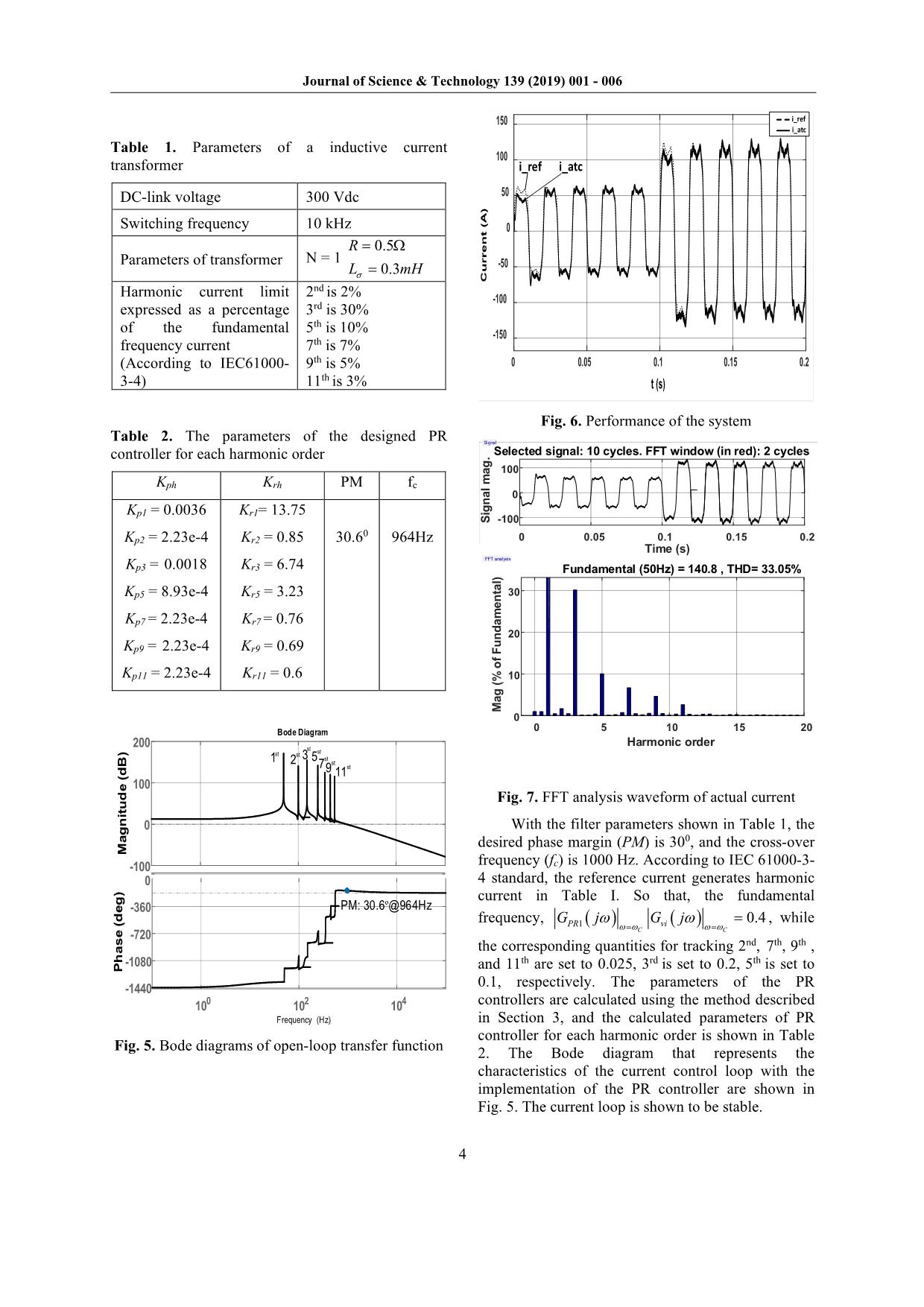
 According to regulations [7], the 
harmonics content of primary current should not 
exceed a certain level. 
The standard IEC 60044-1 [8] addresses CTs 
and gives requirements only under sinusoidal 
conditions and does not give any requirements in 
non-sinusoidal conditions. The standards about power 
quality measurements, IEC 61000-4-30 or IEC 
61000-4-7 [9]-[12], suggest using the frequency 
response test to characterize the behavior under non-
sinusoidal conditions. Manufacturers do not declare 
the frequency response as a specification for the CTs. 
It is possible to find the frequency response as a 
specification only if the CTs are tested with a power 
quality instrument. 
1
N
INPUT
220 Vac
50Hz
2
CONTROL AND
DIAGNOSTIC
CIRCUIT
INPUT
FILTER
MAIN
SWITCH
INITIAL
CHARGE
THREE-
PHASE
BRIDGE
DC FILTER
INVERTER
DC/AC
PWM
F137
DC
OUTPUT
FILTER L3
POWER
TRANSFORMER
TR
TV3
TA2 TA3AC
3 4 5 6 7
8
VDC
VOUT
I OUT
I OUT
I GBT
I prim
Fig. 2. Overall system of the inductive current transformer harmonic tester
One simple approach is to feed the primary 
conductor with a high harmonic content and to 
measure its secondary response. 
To obtain a correct harmonics content of the 
current source, regulators are used. One of recent 
developments is Propositional – Resonant (PR) 
controller [13]-[17]. Recently, PR controllers have 
been suggested as an alternative option for PI 
controllers in grid-connected VSI applications. PR 
controllers have an infinite gain at a selected resonant 
frequency; thus, the zero steady-state error or the 
harmonic at this frequency can be eliminated. The 
parameters of the PR controller are designed in the 
frequency domain, considering the desired system 
phase margin and guaranteeing system stability [15], 
which is usually the fundamental frequency. So that, 
this paper proposes a generalized design method for 
PR current controllers containing multiple resonant 
components in an inductive current transformer to 
generate desired harmonics current. 
2. Control scheme 
2.1. Modelling of inductive current transformer 
The equivalent impedance referred to the 
primary side of the transformer is given as follows: 
( ) ( )2 2 1eqS p s p sZ r N r j x N x R j Lσ σ σω= + + + = + (1) 
where N is the turns ratio of transformer, pr and 
sr are the resistances of the primary and secondary 
sides, px and sx are the leakage inductances of the 
primary and secondary sides. 
Xmrm
Xσp N2rs N
2Xσp
S4
S1
S2
S3
Udc
+
-
-
+
vp
ip
rp
Fig. 3. Equivalent circuit of per phase and series 
connected transformer [13]. 
The plant transfer function of the current control loop 
in inductive current transformers is determined as 
follows: 
( ) ( )
( )
1p
iv
p
i s
G s
v s L s Rσ
= =
+
 (2) 
Journal of Science & Technology 139 (2019) 001 - 006 
3 
2.2. Parameters of PR controller 
The proportional resonant (PR) controller 
provides gains at a certain frequency (resonant 
frequency) and eliminates steady-state errors [13]-
[17]. Therefore, the PR controller can be successfully 
applied to inductive current transformers. The 
transfer function of an ideal PR controller is given as 
follows: 
 ( ) 2 2rhPR ph
h
K s
G s K
s ω
= +
+
(3) 
where phK , rhK , and hω are the proportional gain, 
resonant gain, and frequency for the h-order 
harmonic, respectively. 
Examples of Bode diagram of several PR 
controllers with the fundamental resonant frequency 
are shown in Fig. 4. In this practice, Kph is set to 1, 
Krh is set to 100, 1000, and 10000, respectively. 
-50
0
50
100
150
200
250
300
350
400
M
a
g
n
it
u
d
e
 (
d
B
)
-90
-45
0
45
90
P
h
a
s
e
(d
e
g
)
Bode Diagram
10-2 10-1 100 101 102 103 104
Frequency 
(Hz)
Krh = 100
Krh = 1000
Krh =10000
Fig. 4. Bode diagrams of PR controllers with the 
fundamental resonant frequency. 
The frequency response characteristics of the PR 
controller at the selected resonant frequency are 
calculated as follows: 
( )
( )
( )
22 2 2 2 2
2 2
P h rp
PR
h
K K
G j
ω ω ω
ω
ω ω
− +
=
−
 (4) 
( ) ( )2 2
arctan rhRP
P h
K
G j
K
ω
ω
ω ω
 
 ∠ =
−  
 (5) 
A simple transfer function of the HC and PR 
controller which allows to control specific could be 
rewritten as follows: 
( ) ( ) ( ) ( ) ( )1 3 5 7
2 2
1,3,5,7,... 1,3,5,7,...
PR PR PR PR PR
rh
ph
h h h
G s G s G s G s G s
K s
K
s ω= =
= + + +
= +
+∑ ∑
(6) 
The magnitude-frequency response of the system is 
unity at the cross-over frequency (fc), and fc is higher 
than the fundamental frequency (50Hz). As a result, 
according to Fig. 4, the magnitude-frequency 
response of PR controller simplifies the calculation of 
controller gain Kph of PR as follows: 
( ) ( )
( )
1,3,5,7,...
1,3,5,7,...
1
1
C C
C
PRh vi
h
ph
h vi
G j G j
K
G j
ω ω ω ω
ω ω
ω ω
ω
= =
=
= =
 
= 
 
→ ≈
∑
∑
(7) 
The unity gain of the PR controller can be divided 
among harmonic orders. According to IEC61000-3-4, 
if the tracking for the fundamental current is given 
a higher priority compared to other harmonic orders, 
( ) ( )1
C C
PR viG j G jω ω ω ωω ω= = is given the highest 
value while the corresponding quantities for tracking 
2nd, 5th, and hth can be set to smaller values. 
The parameter rhK of the PR controller is 
determined based on the desired value PM of the 
system’s open-loop transfer function the cross-over 
frequency cω , which is given as follows: 
( ) ( ) 180
C C
PRh viPM G j G jω ω ω ωω ω= == ∠ + + ° (8) 
Therefore, the parameter rhK of the PR regulator is 
determined as follows: 
( )
( ) ( )
2 2
2 2
arctan
tan
rh c
c
ph h c
c ph h c
rh
c
K
A
K
A K
K
ω
ω ω
ω ω
ω
 
  =
−  
−
→ =
 (9) 
where ( ) 180
C
c c viA PM G j ω ωω =
 = − + °
 
. 
The relation between the cross-over frequency fc and 
the sampling frequency fs is 
10
s
c
f
f ≤ . 
3. Simulation and analysis 
The simulation of the proposed design method 
for PR current controllers for inductive current 
transformers is carried out in 
Matlab/Simulink/Simpower. The parameters of the 
test system are shown in Table 1. 
Journal of Science & Technology 139 (2019) 001 - 006 
4 
Table 1. Parameters of a inductive current 
transformer 
DC-link voltage 300 Vdc 
Switching frequency 10 kHz 
Parameters of transformer N = 1 
0.5
0.3
R
L mHσ
= Ω
=
Harmonic current limit 
expressed as a percentage 
of the fundamental 
frequency current 
(According to IEC61000-
3-4) 
2nd is 2% 
3rd is 30% 
5th is 10% 
7th is 7% 
9th is 5% 
11th is 3% 
Table 2. The parameters of the designed PR 
controller for each harmonic order 
Kph Krh PM fc 
Kp1 = 0.0036 
Kp2 = 2.23e-4 
Kp3 = 0.0018 
Kp5 = 8.93e-4 
Kp7 = 2.23e-4 
Kp9 = 2.23e-4 
Kp11 = 2.23e-4 
Kr1= 13.75 
Kr2 = 0.85 
Kr3 = 6.74 
Kr5 = 3.23 
Kr7 = 0.76 
Kr9 = 0.69 
Kr11 = 0.6 
30.60 
964Hz 
-100
0
100
200
M
ag
n
it
u
d
e
 (d
B
)
100 102 104
-1440
-1080
-720
-360
0
P
h
as
e
 (d
eg
)
Bode Diagram
Frequency (Hz)
PM: 30.6º@964Hz
1st 2st 3
st
5st
9st7
st
11st
Fig. 5. Bode diagrams of open-loop transfer function 
0 0.05 0.1 0.15 0.2
 t (s)
-150
-100
-50
0
50
100
150
C
u
rr
e
n
t 
(A
)
i_ref
I_atc
i_ref
i_atc
i_ref i_atc
Fig. 6. Performance of the system 
Signal
0 0.05 0.1 0.15 0.2
Time (s)
-100
0
100
Si
gn
al
 m
ag
. Selected signal: 10 cycles. FFT window (in red): 2 cycles
FFT analysis
0 5 10 15 20
Harmonic order
0
10
20
30
M
ag
 (%
 of
 Fu
nd
am
en
ta
l)
Fundamental (50Hz) = 140.8 , THD= 33.05%
Fig. 7. FFT analysis waveform of actual current 
With the filter parameters shown in Table 1, the 
desired phase margin (PM) is 300, and the cross-over 
frequency (fc) is 1000 Hz. According to IEC 61000-3-
4 standard, the reference current generates harmonic 
current in Table I. So that, the fundamental 
frequency, ( ) ( )1 0.4
C C
PR viG j G jω ω ω ωω ω= = = , while 
the corresponding quantities for tracking 2nd, 7th, 9th , 
and 11th are set to 0.025, 3rd is set to 0.2, 5th is set to 
0.1, respectively. The parameters of the PR 
controllers are calculated using the method described 
in Section 3, and the calculated parameters of PR 
controller for each harmonic order is shown in Table 
2. The Bode diagram that represents the 
characteristics of the current control loop with the 
implementation of the PR controller are shown in 
Fig. 5. The current loop is shown to be stable. 
Journal of Science & Technology 139 (2019) 001 - 006 
5 
Table 3. List of actual current harmonics in 0.04s – 
0.08s 
Harmonic 
order 
ercentage of the 50 
Hz input current (%) 
Phase 
2 2.08 171.40 
3 29.96 179.30 
5 10.06 1790 
7 6.67 1660 
9 5.15 149.80 
11 3.03 126.70 
Table 4. List of actual current harmonics in 0.14s – 
0.18s. 
Harmonic 
order 
Percentage of the 50 
Hz input current (%) 
Phase 
2 1.94 175.70 
3 29.95 179.70 
5 10.03 179.30 
7 6.81 172.90 
9 5.16 164.20 
11 3.12 150.90 
Unipolar pulse-width-modulation technique is 
also implemented to control the switching of the 
IGBT switches of the single-phase VSI [21]. The 
reference root mean square current (iref) is changed 
from 50A to 100A at 0.1s. Simulation results in Fig. 6 
show that the response of the current (iact) tracks the 
reference in one power grid cycle (20ms). Besides, 
the efficiency of the proposed control scheme of the 
inductive current transformer is proven, and the 
ability of generating the correct content of current 
source compatible with the selective harmonics 
satisfies international standards in Fig. 7, Table III 
and Table IV. 
4. Conclusion 
In this paper, we have successfully implemented 
PR current controllers for the selective harmonics 
generator. This technique has been tested on a testbed 
to test the current transformer with different 
harmonics content. 
Acknowledgments 
This research is funded by MOIT through the 
project DTKHCN.215/17 under contract number 
162.17.DT/HĐ-KHCN. The authors would like to 
thank MOIT and HUST for their financial support of 
this study. 
References 
[1] B. A. Luciano, R. C. Silverio Freire, J. G. de Assis 
Lira, G. Fontgalland, and W. B. de Castro; Current 
Transformer with Toroidal Nanocrystalline Alloy 
Core; IEEE Lat. Am. Trans., 2006. 
[2] M. Kaczmarek; Inductive current transformer 
accuracy of transformation for the PQ measurements; 
Electr. Power Syst. Res., vol. 150, pp. 169–176, Sep. 
2017. 
[3] M. Kaczmarek; Wide Frequency Operation of the 
Inductive Current Transformer with Ni80Fe20 
Toroidal Core; Electr. Power Components Syst., 
2014. 
[4] M. Kaczmarek and S. Jama; Accuracy of inductive 
voltage transformer in the presence of voltage high 
harmonics; in ICHVE 2014 - 2014 International 
Conference on High Voltage Engineering and 
Application, 2014. 
[5] Z. Spoljaric, V. Jerkovic, and M. Stojkov; 
Measurement system for transformer inrush current 
higher harmonics determination; in 23rd DAAAM 
International Symposium on Intelligent 
Manufacturing and Automation 2012, 2012, vol. 2. 
[6] Cataliotti, D. Di Cara, P. A. Di Franco, A. E. 
Emanuel, and S. Nuccio; Frequency response of 
Measurement Current Transformers; in 2008 IEEE 
Instrumentation and Measurement Technology 
Conference, 2008, pp. 1254–1258. 
[7] S. M. Halpin; Comparison of IEEE and IEC 
Harmonic Standards; in IEEE Power Engineering 
Society General Meeting, 2005, 2005, pp. 2732–
2734. 
[8] IEC, IEC 60044-1 Instrument transformers Part 1 
Current transformers, Iec 60044-1, 2003. 
[9] R. Neumann; The importance of IEC 61000-4-30 
Class A for the coordination of power quality levels: 
Is it important?; in 2007 9th International Conference 
on Electrical Power Quality and Utilisation, EPQU, 
2007. 
[10] IEC, IEC 61000-4-30 Electromagnetic compatibility 
(EMC) – Part 4-30: Testing and measurement 
techniques – Power quality measurement methods. 
IEEE, 2000. 
[11] International Electrotechnical Commission - IEC-, 
International Standard IEC 61000-4-5 
Electromagnetic compatibility (EMC), Testing and 
measurement techniques-Surge immunity test. 2005. 
[12] International Electrotechnical Commission, 
Electromagnetic compatibility (EMC) Part 4-15: 
Testing and measurement techniques - Flickermeter - 
Functional and design specifications, IEC 61000-4-
15, 2011. 
[13] Phuong Vu , Ngoc Dinh, Nam Hoang, Quan Nguyen, 
Dich Nguyen, Minh Tran; A Generalized Parameter 
Tuning Method of Proportional-Resonant Controllers 
for Dynamic Voltage Restorers; International Journal 
of Power Electronics and Drive System, Vol 9, No 4, 
December 2018. 
[14] D. Zammit, C. Spiteri Staines, M. Apap, and J. Licari; 
Design of PR current control with selective harmonic 
Journal of Science & Technology 139 (2019) 001 - 006 
6 
compensators using Matlab; J. Electr. Syst. Inf. 
Technol., vol. 4, no. 3, pp. 347–358, Dec. 2017. 
[15] N. Zhang, H. Tang, and C. Yao; A systematic method 
for designing a PR controller and active damping of 
the LCL filter for single-phase grid-connected PV 
inverters; Energies, vol. 7, no. 6, pp. 3934–3954, 
2014. 
[16] Y. Song, J. Wang, and A. Monti; Design of 
systematic parameter tuning approaches for multiple 
proportional-resonance AC current regulator; in 2015 
IEEE 6th International Symposium on Power 
Electronics for Distributed Generation Systems, 
PEDG 2015, 2015. 
[17] R. Teodorescu, F. Blaabjerg, U. Borup, and M. 
Liserre; A new control structure for grid-connected 
LCL PV inverters with zero steady-state error and 
selective harmonic compensation; in Nineteenth 
Annual IEEE Applied Power Electronics Conference 
and Exposition, 2004. APEC ’04., vol. 1, pp. 580–
586. 
[18] F. De Bosio, L. A. D. S. Ribeiro, M. S. Lima, F. 
Freijedo, J. M. Guerrero, and M. Pastorelli; Inner 
current loop analysis and design based on resonant 
regulators for isolated microgrids; in 2015 IEEE 13th 
Brazilian Power Electronics Conference and 1st 
Southern Power Electronics Conference, 
COBEP/SPEC 2016, 2015, pp. 1–6. 
[19] M. S. Lima, L. A. D. S. Ribeiro, and J. G. De Matos; 
Comparison analysis of resonant controllers in 
discrete domain taking into account the computational 
delay; in 2015 IEEE 13th Brazilian Power Electronics 
Conference and 1st Southern Power Electronics 
Conference, COBEP/SPEC 2016, 2015. 
[20] Phuong Vu, Quan Nguyen, Minh Tran, Duong Tuan, 
Hung Tran; A systematic design of PR current 
controllers for single-phase LCL-type grid-connected 
inverters under distorted grid voltage; Journal of 
Electrical Systems, Vol 14 Issue 3, (September 
2018), . 
[21] R. Teodorescu, M. Liserre, and P. Rodrguez, Grid 
converters for photovoltaic and wind power systems. 
John Wiley, Ltd, 2011.