Phát triển phần mềm mô phỏng hệ thống điện smart_simulator

i thuật toán Newton-Rapson. Quá trình kết hợp này được khởi động bằng thuật toán 
Gauss-Seidel với một số bước lặp nhất định, nhằm tìm kiếm tập nghiệm ban đầu khả thi 
tốt nhất cho thuật toán Newton-Rapson, mô phỏng tự động chuyển tiếp qua thuật toán 
Newton-Rapson. Kết quả là quá trình mô phỏng được tăng tốc, đảm bảo mô phỏng 
thành công, vì thế gọi là “Smart_Simulator”. 
2.A. Mô phỏng theo Gauss-Seidel trong “S_S” 
Biểu thức công suất phức tính toán bơm vào nút i được tính theo (5) 
 niniiiiiikn
k
ikicalcicalci VYVYVYVYVVYVjQP 
........2211
*
1
*
,, (5) 
Trong đó vec tơ *iV là liên hợp của vectơ điện áp Vi; Yik là điện dẫn tương hỗ giữa 
nút i và vút k. Các đại lượng phức tương ứng của nút i trong (5) là điện áp, điện dẫn 
riêng, điện dẫn tương hỗ lần lượt có giá trị như sau (trong S_S có chương trình con tính 
ma trận điện dẫn [Y]). 
(cos sin )i i i i i iV V V j    (i) 
(cos sin ) Gii ii ii ii ii ii ii iiY Y Y j jB    (ii) 
(cos sin ) Gij ij ij ij ij ij ij ijY Y Y j jB    (iii) 
Vì mong muốn tìm ni VVVVV ,....,...,, 32 để calicali jQP ,, = injiinji jQP ,, từ 
(5) ta có 
  niniiiiiikn
k
ikicnjiinji VYVYVYVYVVYVjQP 
........2211
*
1
*
,, (6) 
Trong (6), vế trái injiinji jQP ,, là công suất hữu công, vô công thực bơm vào nút i 
là các dữ liệu cho trước. Sắp xếp lại biểu thức (6) ta có thể tính vecto điện áp nút i Vi khi 
biết giá trị công suất hữu công và công suất vô công bơm vào nút i Pi,inj và Qi,inj. 
,inj ,inj
1 1 2 2
1 ...i ii i i in n
ii i
P jQ
V Y V Y V Y V
Y V 
 (7) 
BÁO CÁO CHUNG | 103 
“S_S” dùng (7) để tính tập vecto điện áp nút ni VVVVV ,....,...,, 32 . Giá trị 
môđun và góc pha điện áp sau mỗi bước tính lặp được dùng để tính các giá trị công suất 
tính toán theo (5), từ đó tính sai lệch công suất theo (2) và (3). Quá trình tính lặp sẽ làm 
giảm dần ΔPi và ΔQi cho tới khi các giá trị này nhỏ hơn một sai lệch mong muốn để kết 
thúc quá trình mô phỏng CĐXL. Để tăng nhanh quá trình mô phỏng, tính điện áp các 
nút theo (6) được nhân với một hằng số λ được gọi là hệ số gia tốc (acceleration factor). 
Giá trị hằng số λ thường trong khoảng 1.2 đến 1.4. Khi đó, giá trị điện áp gia tốc của nút 
i, ở bước tính lặp thứ k tính theo (8) 
 ( ) ( 1) ( ) ( 1) ( ) ( 1), , , ,(1 )k k k k k ki acc i acc i i acc i i accV V V V V V   (8) 
2.B. Mô phỏng Newton-Rapson trong “S_S” 
Ta xét một HTĐ có n nút, trong đó số nút loại P-Q là np và số nút loại P-V là ng 
để có n = np + ng + 1 với nút số 1 là nút cân bằng. 
Trong “S_S”, cách tiếp cận mô phỏng CĐXL theo phương pháp Newton-Rapson 
tương tự như giải hệ phương trình phi tuyến dùng phương pháp Newton-Rapson tức là 
tại mỗi bước tính lặp, ta phải lập một ma trận Jacobian và giải hệ phương trình điều 
chỉnh để tìm các giá trị hệ số hiệu chỉnh cho các biến. Quá trình hiệu chỉnh, tính lặp tiếp 
tục cho đến khi tìm được giá trị các biến thoả mãn hệ phương trình phi tuyến cần giải. 
Đối với mô phỏng CĐXL, hệ phương trình tuyến tính điều chỉnh để tìm các giá trị 
hệ số hiệu chỉnh cho các biến điện áp nút là mô đun điện áp |Vi| và góc lệch điện áp δi 
dưới dạng ma trận: 
2
2
2
2 2
11
1
oo
o
n
n
nn
n
P
V P
J V Q
QV
V




 
 (9) 
Trong đó J là ma trận Jacobian; i i = 2, 3,, n là giá trị hệ số hiệu chỉnh 
góc lệch điện áp δi và   i
i
V
V 
 là giá trị hệ số hiệu chỉnh mô đun điện áp |Vi|; 
ΔPi, ΔQi i = 2, 3,, n lần lượt là sai lệch công suất hữu công, vô công tại nút i 
tính theo (2) và (3). 
104 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
Trong “S_S”, giải hệ phương trình tuyến tính điều chỉnh (9) để tìm các giá trị hệ 
số hiệu chỉnh Δ δ (0) và Δ |V| (0) / |V| (0) được thực hiện theo phép nghịch đảo ma trận 
  1 J 
  
Q
PJ
VV
1
/
 (10) 
Ma trận J gồm bốn ma trận con. 
11 11
21 22
J J
J
J J
Kích thước hay cấp ma trận Jacobian là ma trận vuông (n + np − 1) x (n + np −1). 
Kích thước của các ma trận con lần lượt là J11: (n 1) (n 1), J12: (n 1) np, J21: np 
 (n 1) và J22: np np. Các phần tử ma trận con là các giá trị đạo hàm riêng của hàm 
Pi, Qi theo các biến góc lệch điện áp δi và mô đun điện áp |Vi|. Các phần tử ma trận 
Jacobian cho trong bảng 1. 
2 2
2
11
2
n
n n
n
P P
J
P P
 
 
        

  

Bảng 1.1. Các phần tử ma trận J11 
1
1
1
1
2 2
2
2
12
2
2
2
no
no
no
no
n
P PV V
V V
J
PPV V
V V
       

  

Bảng 1.2. Các phần tử ma trận J12 
2 2
2
21
1 1
2
o o
n
n n
n
Q Q
J
Q Q
 
 
        

  

Bảng 1.3. Các phần tử ma trận J21 
1
1
1
1
2 2
2
2
22
1 1
2
2
no
no
o o
no
no
n n
Q QV V
V V
J
Q Q
V V
V V
        

  

Bảng 1.4. Các phần tử ma trận J22 
Bảng 1. Các phần tử ma trận Jacobian 
Để xác lập biểu thức tính giá trị các đạo hàm riêng trong bảng 1, từ biểu thức công 
suất phức tính toán bơm vào nút i tính theo (5) biến đổi và sắp xếp lại theo phần thực Pi, 
và phần ảo Qi. 
BÁO CÁO CHUNG | 105 
2
1
1
cos( )
n
i i ii ik i k ik k i
k
k
P V G Y VV   
  (11) 
2
1
1
sin( )
n
i i ii ik i k ik k i
k
k
Q V B Y VV   
  (12) 
Các biểu thức (11) và (12) dùng để xác định biểu thức tính đạo hàm riêng trong 
bảng 1 là các phần tử ma trận Jacobian. 
Thành lập ma trận Jacobian 
Các biểu thức (11) và (12) được dùng để tính giá trị các phần tử các ma trận con. 
B.1. Lập ma trận J11 
Ma trận con J11 có dạng sau: 
22 2
21
n
n nn
L L
J
L L

  

Từ bảng 1.1 thấy rằng các Lik là đạo hàm riêng của Pi đối với δk. Đạo hàm riêng 
của Pi theo (11) với k ≠ i sẽ là: 
 sin( ),iik ik i k ik k i
k
PL Y VV i k  
  (13) 
Tương tự, đạo hàm riêng của Pi theo (11) với k = i sẽ là: 
1
1
sin( )
n
i
ii ik i k ik k i
ki
k
PL Y VV    
   
So sánh biểu thức trên với (12) ta có thể viết: 
 2iii i i ii
i
PL Q V B
  (14) 
B.2. Lập ma trận J21 
Ma trận con J21 có dạng sau: 
22 2
21
2o o
n
n n n
M M
J
M M

  

106 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
Từ bảng 1.3 thấy rằng các phần tử của J21 là đạo hàm riêng của Q đối với δ. Từ 
(12) ta có: 
 cos( ),iik ik i k ik k i
k
QM Y VV i k  
  (15) 
Tương tự, đạo hàm riêng của Qi với k = i sẽ là: 
 2
1
1
cos( )
n
i
ii ik i k ik k i i i ii
ki
k
QM Y VV P V G   
   (16) 
 B.3. Lập ma trận J12 
Ma trận con J12 có dạng sau: 
22 2
12
2
o
o
n
n nn
N N
J
N N

  

Từ bảng 1.2 thấy rằng các phần tử của J12 là đạo hàm riêng của P đối với môđun 
điện áp |V|. Với i ≠ k, từ (11) ta có: 
 cos( ) ,iik k ik i k ik k i ik
k
PN V Y VV M i k
V
    (17) 
Với k = i ta có: 
1
1
2 cos( )
n
i
ii i i i ii ik k ik k i
ki
k
PN V V V G Y V
V
  
   
 
 2 2
1
1
2 cos( ) 2
n
i ii ik i k ik k i i ii ii
k
k
V G Y VV V G M  
  (18) 
B.4. Lập ma trận J22 
Ma trận con J22 có dạng sau: 
22 2
22
2
o
o o o
n
n n n
O O
J
O O

  

Từ bảng 1.4 thấy rằng các phần tử của J22 là đạo hàm riêng của Q đối với môđun 
điện áp |V|. Với i ≠ k, từ (12) ta có: 
BÁO CÁO CHUNG | 107 
 sin( ) ,iik i i ik i k ik k i ik
k
QO V V Y VV L i k
V
    (19) 
Với k = i, ta có: 
1
1
2 sin( )
n
i
ii i i i ii ik k ik k i
kk
k
QO V V V B Y V
V
  
   
 
 2 2
1
1
2 sin( ) 2
n
i ii ik i k ik k i i ii ii
k
k
V B Y VV V B L  
  (20) 
Như vậy, một khi các ma trận con J11 và J21 đã được tính thì việc lập các ma trận 
con J12 và J22 là khá dễ dàng. Thật vậy, J12 có thể được lập từ J11 nhờ (17) và (18); 
J22 có thể được lập từ J21 nhờ (19) và (20). Điều này rất có ý nghĩa về tiết kiệm thời gian 
tính toán đối với các HTĐ lớn. 
Các bước mô phỏng CĐXL theo phương pháp Newton-Raphson trong “S_S”: 
Bước 1: Chọn giá trị ban đầu môđun điện áp V| (0)của tất cả np nút loại P-Q và 
n − 1 góc pha ban đầu δ (0) của tất cả các nút trừ nút cân bằng. Bước 1 rất quan trọng, 
bởi vì nếu các giá trị ban đầu chọn không phù hợp, cách xa giá trị thực của vecto điện 
áp nút ni VVVVV ,....,...,, 32 sẽ không thực hiện được bước 5, không tìm được các 
giá trị hệ số hiệu chỉnh Δ δ (0) và Δ |V| (0) / |V| (0) tính theo (10). Khi đó ta nói rằng mô 
phỏng không hội tụ. “Smart_Simulator” chính là giải pháp để đảm bảo rằng nếu không 
có sai sót về dữ liệu của HTĐ, mô phỏng sẽ thành công. Xin xem phần “C. Mô phỏng 
Smart_Simulator trong “S_S” ở phía dưới. 
Bước 2: Dùng các giá trị ban đầu |V|(0) và δ (0) thay vào (11) để tính (n – 1) công 
suất hữu công bơm vào Pcalc(0) và các sai lệch công suất hữu công ΔP (0). 
Bước 3: Dùng các giá trị ban đầu |V|(0) và δ (0) thay vào (12) để tính np công suất 
vô công bơm vào Qcalc(0) và các sai lệch công suất hữu công ΔQ (0). 
Bước 4: Dùng các giá trị ban đầu |V|(0) và δ (0) để thành lập ma trận Jacobian [ J (0]] 
tính theo các biểu thức từ (13), (14), (19), (20). 
Bước 5: Tính ma trận nghịch đảo   1 J để tìm các giá trị hệ số hiệu chỉnh Δ δ (0) 
và Δ |V| (0) / |V| (0) tính theo (10). Ma trận [J] và ma trận nghịch đảo   1 J có thể được 
dùng trong nhiều bước tính lặp liên tiếp mà không cần tính lại. Nói cách khác, bước 4 
và bước 5 chỉ phải tính lại sau một số lần tính lặp. Vì thế tiết kiệm thời gian mô phỏng 
rất đáng kể. 
 Bước 6: Hiệu chỉnh, cập nhật góc pha và môđun điện áp tính theo: 
(1) (0) (0)   (21) 
108 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
(0)
(1) (0)
(0)1
V
V V
V
 (22) 
Bước 7: Kiểm tra nếu tất cả các sai lệch công suất ΔP, ΔQ bé hơn một sai lệch 
nhỏ cho trước, quá trình mô phỏng kết thúc. Nếu không, trở lại bước 1 để bắt đầu một 
bước tính lặp tiếp theo với các giá trị cập nhật góc pha và môđun điện áp tính theo (21) 
và (22). 
2.C. Mô phỏng Smart_Simulator trong “S_S” 
Hình 1: “Smart_Simulator” kết hợp mô phỏng Gauss-Seidel & Newton-Rapson 
“Smart_Simulator” kết hợp thuật toán Gauss-Seidel với thuật toán Newton-
Rapson. Quá trình kết hợp này được khởi động bằng thuật toán Gauss-Seidel với một số 
bước lặp nhất định, nhằm tìm kiếm tập nghiệm ban đầu )0()0( ; iiV  tốt nhất cho thuật toán 
Newton-Rapson, mô phỏng tự động chuyển tiếp qua thuật toán Newton-Rapson. Kết 
quả là quá trình mô phỏng được tăng tốc, đảm bảo mô phỏng thành công, vì thế gọi là 
“Smart_Simulator, xem hình 1. 
2.D. Các chức năng chính trong “S_S” 
S_S được lập trình trong môi trường VBA & Excel vì thế giao diện Input & 
Output rất đơn giản, rõ ràng và thân thiện. Các nút điều khiển kích hoạt các chức năng 
được đặt trong từng trang, tương tác giữa các trang và các kết quả mô phỏng được trình 
bày trong bảng hoặc biểu đồ Excel (xem hình 2). S_S rất dễ dàng cập nhật, mở rộng 
chương trình theo yêu cầu tuỳ biến. 
)0()0( ; iiV 
BÁO CÁO CHUNG | 109 
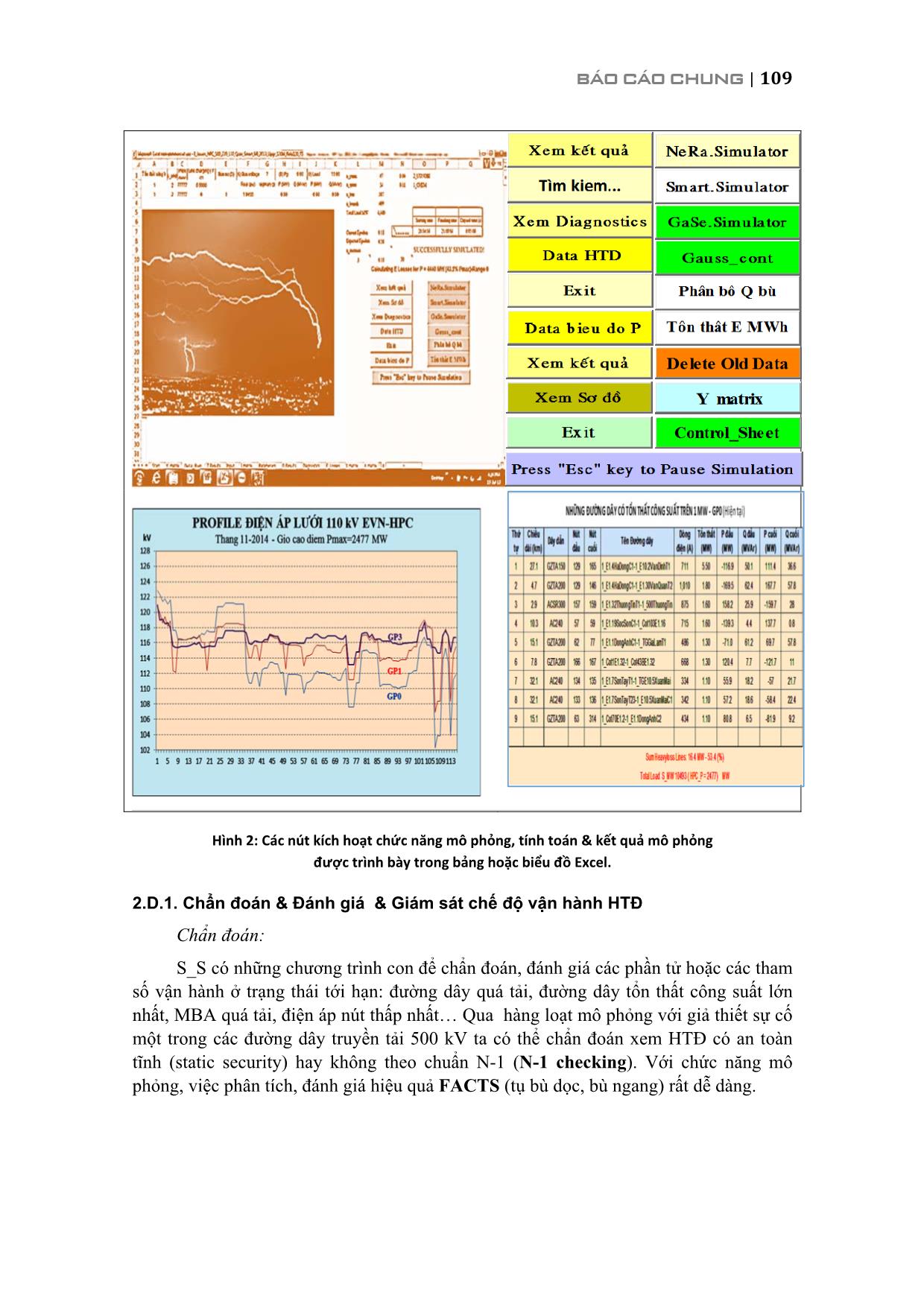
Hình 2: Các nút kích hoạt chức năng mô phỏng, tính toán & kết quả mô phỏng 
được trình bày trong bảng hoặc biểu đồ Excel. 
2.D.1. Chẩn đoán & Đánh giá & Giám sát chế độ vận hành HTĐ 
Chẩn đoán: 
S_S có những chương trình con để chẩn đoán, đánh giá các phần tử hoặc các tham 
số vận hành ở trạng thái tới hạn: đường dây quá tải, đường dây tổn thất công suất lớn 
nhất, MBA quá tải, điện áp nút thấp nhất Qua hàng loạt mô phỏng với giả thiết sự cố 
một trong các đường dây truyền tải 500 kV ta có thể chẩn đoán xem HTĐ có an toàn 
tĩnh (static security) hay không theo chuẩn N-1 (N-1 checking). Với chức năng mô 
phỏng, việc phân tích, đánh giá hiệu quả FACTS (tụ bù dọc, bù ngang) rất dễ dàng. 
110 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
Đánh giá: 
Chương trình con đánh giá tổn thất điện năng của từng cấp điện áp, tổn thất điện 
năng từng khu vực, từng đường dây, chỉ ra điện áp thực tế tại các nút trên lưới điện, 
dòng điện trên các nhánh, tình trạng mang tải của các đường dây cùng một chủng loại 
Giám sát: 
Chương trình con giám sát vận hành tối ưu MBA ở các trạm có nhiều hơn 1 
MBA. 
2.D.2. Phân bố tụ bù Q 
Thuật toán xác định dung lượng đặt tụ bù (MVAr) ở từng trạm là bao nhiêu dựa 
trên khái niệm “độ nhạy” hay hệ số hiệu quả đặt bù của mỗi trạm j. “Độ nhạy” hay giá 
trị hệ số hiệu quả đặt bù của một trạm j được định nghĩa theo biểu thức:
jb
tt
j Q
P
HQ 
Trong đó, HQj là giá trị “độ nhạy” hay hệ số hiệu quả đặt bù của trạm j; Ptt là tổng 
tổn thất công suất của lưới truyền tải; ∆Ptt là gia số giảm tổn thất công suất của toàn bộ 
lưới truyền tải điện (MW) khi có ∆Qb đặt vào nút j; ∆Qbj là gia số dung lượng TBB 
(MVAr) đặt vào nút j. Khi click vào nút Phân bố Q bù sẽ phân phối dung lượng TBB 
theo véc tơ gradient F
 {HQ1, HQ2, HQj, HQN} 
2.D.3. Đánh giá tổn thất điện năng 
Từ biểu đồ phụ tải P giờ của cả tháng (ví dụ 24 giờ x 30 ngày = 720 giá trị) và 
điện năng tháng phân tích thành biểu đồ giải công suất và số giờ tương ứng với giải 
công suất HTĐ vận hành (hình D.3). Tổn thất công suất ∆P của các giải công suất có 
được từ kết quả mô phỏng HTĐ. Khi biết giá trị tổn thất công suất ∆P và số giờ vận 
hành tương ứng, thì việc đánh giá tổn thất điện năng tháng theo biểu thức: 
 )()()(
1
hourHMWPMWhE ii
N
i
 
Trong đó ∆E là tổn thất điện năng tháng (MWh); ∆Pi và Hi lần lượt là giá tổn thất 
công suất và số giờ vận hành của HTĐ tại giải công suất i trên hình D.3; N là số giải 
công suất, trong trường hợp cụ thể N = 16. S_S có thể đánh giá tổn thất điện năng từng 
cấp điện áp, tổn thất điện năng từng khu vực, từng đường dây. 
BÁO CÁO CHUNG | 111 
Hình 3: Giải công suất HTĐ vận hành trong một tháng 
3. KẾT LUẬN 
Smart_Simulator là sản phẩm phần mềm mô phỏng, phân tích, đánh giá chế độ 
xác lập hệ thống điện được lập trình trong môi trường VBA & Excel. S_S có nhiều chức 
năng như đã trình bày trong phần “2.D. Các chức năng chính trong S_S”. Hiện tại, 
S_S đang được sử dụng để mô phỏng, phân tích, tính toán tổn thất điện năng, chẩn đoán 
tình trạng vận hành và đánh giá phát triển lưới 110 kV (có tính đến HTĐ 500, 220 kV 
liên quan) của EVN-NPC, EVN-HPC, EVN-SPC. S_S cũng đang được dùng để mô 
phỏng, phân tích, tính toán tổn thất điện năng, đánh giá vận hành và đánh giá phát triển 
lưới phân phối trung áp của các Công ty điện lực thuộc EVN-NPC, EVN-HPC. Ngoài 
ra S_S còn có thể dùng cho mục đích đào tạo kỹ sư nghiên cứu, vận hành HTĐ, vận 
hành lưới phân phối trung áp. 
4. LỜI CẢM ƠN 
Các tác giả phát triển phần mềm mô phỏng HTĐ “Smart_Simulator” chân thành 
cảm ơn Tổng Công ty Điện lực miền bắc EVN-NPC, Tổng Công ty Điện lực Hà Nội 
EVN-HPC đã tài trợ, tổ chức đào tạo kỹ sư và sử dụng hiệu quả S_S trong mô phỏng, 
phân tích, tính toán, đánh giá vận hành và đánh giá phát triển lưới cao thế 110 kV và 
lưới phân phối trung áp của các công ty điện lực thuộc EVN-NPC, EVN-HPC. Cảm ơn 
Tạp chí “Điện & Đời sống” - Hội Điện lực Việt Nam trong việc đăng tải và tạo điều kiện 
thảo luận các bài báo có liên quan đến sử dụng “S_S” trong khảo sát HTĐ Việt Nam. 
TÀI LIỆU THAM KHẢO 
[1] Professor Arindam Ghosh 
system/ui/About-Faculty.html 
[2] Tài liệu hướng dẫn sử dụng softwre Smart_Simulator.