Phát triển công thức lai tích phân - Vi phân 3D dựa trên véc tơ điện thế - ứng dụng cho bài toán có cấu trúc vỏ mỏng dẫn điện

 method was validated and proved applicable in practical problems. Các phương pháp số thường được áp dụng trong mô 
 Keywords: Electromagnetics, conductive thin shell, eddy current, finite phỏng trường điện từ được chia làm hai loại: Các phương 
element method, numerical integral method. pháp hữu hạn (finite methods) giải hệ phương trình 
 Maxwell dưới dạng vị phân, như là phương pháp phần tử 
Viện Điện, Trường Đại học Bách khoa Hà Nội hữu hạn FEM (Finite Element Method), phương pháp thể 
 tích hữu hạn FVM (Finite Volume Method) và các phương 
Email: tung.leduc1@hust.edu.vn 
 pháp tích phân số giải hệ phương trình Maxwell dưới dạng 
Ngày nhận bài: 02/5/2020 
 tích phân, như là phương pháp tích phân bề mặt BEM 
Ngày nhận bài sửa sau phản biện: 10/6/2020 (Boundary Element Method), phương pháp mô men MoM 
Ngày chấp nhận đăng: 24/6/2020 (Method of Moment), phương pháp PEEC (Partial Element 
 Equivalent Circuit) [5-10]. Việc lựa chọn một trong những 
 phương pháp trên hoàn toàn phụ thuộc vào các hiện tượng 
 TỪ VIẾT TẮT 
 vật lý cần mô phỏng: tần số cao hay thấp, có vật liệu từ hay 
 FEM Phương pháp phần tử hữu hạn không, có xét đến hiệu ứng điện cảm hay điện dung, 
 PEEC Phương pháp mạch điện thay thế tương đương nguồn kích thích ngoài... Tuy nhiên, không có một phương 
 Website: https://tapchikhcn.haui.edu.vn Vol. 56 - No. 3 (June 2020) ● Journal of SCIENCE & TECHNOLOGY 35
 KHOA H ỌC CÔNG NGHỆ P - ISSN 1859 - 3585 E - ISSN 2615 - 961 9 
 pháp là vạn năng và tối ưu trong mọi bài toán và việc lựa  = − (1) 
 chọn phương pháp tốt nhất phụ thuộc vào tính chất thiết 
  =  (2) 
 bị điện và dải hoạt động của nó. 
  =  (3) 
 Trong các phương pháp được mô tả ở trên, phương 
 pháp hữu hạn FEM đã trở thành một phương pháp tổng Phương trình Ampère-Maxwell (2) chứng tỏ sự tồn tại 
 quát cho việc giải các bài toán điện từ như là các bài toán từ một véc-tơ điện thế T được định nghĩa: 
 tĩnh và các bài toán từ động [2]. Hiện nay, phương pháp  =  (4) 
 này được phát triển và thương mại hóa dưới dạng phần Xem xét thành phần pháp tuyến của véc-tơ cảm ứng từ 
 mềm mô phỏng, tiêu biểu là phần mềm Maxwell của công B trên bề mặt Γ, chúng ta có: 
 ty Ansys [3], phần mềm Flux3D của công ty Cedrat [4]. Tuy 
 () ⋅  = − ⋅  (5) 
 nhiên nhược điểm lớn nhất của phương pháp này là phải 
 chia lưới và tính toán vùng không khí. Do đó, khi sử dụng Áp dụng phương pháp Galerkine cho bề mặt Γ, phương 
 phương pháp FEM để mô phỏng 3D các thiết bị điện phức trình dạng tích phân mô tả (5) là: 
 tạp, có nhiều khoảng trống không khí tạo ra các phương 
 () ⋅ Γ = −  ⋅ Γ (6) 
 trình phần tử hữu hạn với số bậc tự do lớn. Điều này làm  
 cho việc giải phương trình bằng máy tính điện tử là rất khó với w là hàm trọng số. 
 khăn thậm chí là không thể thực hiện được. i
 Áp dụng đẳng thức (. ) = .  + () ×
 Bài báo này phát triển công thức lai kết hợp phương , phương trình (6) được viết lại dưới dạng: 
 trình vi phân và tích phân dựa trên véc-tơ điện thế để mô 
 phỏng điện từ trong các cấu trúc có dạng vỏ mỏng dẫn − ( × ) ⋅ Γ + (.) ⋅ Γ
 điện. Vùng vỏ mỏng được mô tả bởi hệ phương trình vi   (7) 
 phân và giải bằng phương pháp FEM, trong khi đó tương = −  ⋅ Γ 
 tác với từ trường ngoài ở vùng không khí được mô phỏng 
 và giải bằng phương pháp tích phân số. Phương pháp này Hoán đổi các bộ phận trong biểu thức của thành phần 
 còn được gọi là phương pháp lai tích phân- vi phân IDM thứ nhất và áp dụng định luật Stokes trong thành phần thứ 
 (Integro-Differential Method). Ưu điểm của phương pháp hai vế trái của phương trình (7), ta thu được: 
 nằm ở chỗ không phải chia lưới vùng không khí bao quanh 
 đối tượng tính toán, giảm thời gian cũng như khối lượng ( × ) ⋅ Γ − Γ =   ⋅ Γ (8) 
 tính toán.   
 Phần tiếp theo của bài báo giới thiệu hệ phương trình ∮ w. . dΓ là tích phân đường theo vòng C bao quanh 
 lai tích phân - vi phân và phương pháp số giải hệ phương bề mặt Γ. Thành phần này có giá trị bằng 0 với điều kiện 
 trình đó. Để kiểm nghiệm phương pháp đã phát triển, hai ví biên [2]. 
 dụ kinh điển đã được mô phỏng và so sánh kết quả trong Như vậy, phương trình (8) trở thành: 
 mục 3. Cuối cùng là kết luận bài báo cũng như các hướng 
 nghiên cứu tiếp theo sẽ được trình bày trong mục 4. ( × ). . dΓ = jω. . . . dΓ (9) 
  
 2. PHƯƠNG PHÁP LAI TÍCH PHÂN - VI PHÂN 
 Từ (3) và (4), chúng ta có: 
 Công thức được phát triển dựa trên nghiên cứu của S.J.  
 Salon [11]. Tuy nhiên, công thức trong [11] có nhược điểm là  = = (10) 
 σ σ
 chỉ áp dụng cho các cấu trúc dạng phẳng. Trong phần này, 
 tác giả phát triển các hệ phương trình cho phép mô phỏng Vậy: 
 1
 điện từ cấu trúc dạng vỏ mỏng trong không gian 3D. ( × ) = ( × ) (11) 
 
 Áp dụng đẳng thức: (.) = ( ⋅ ).  +  ×
  và lưu ý rằng trên bề mặt Γ : n.grads = 0 và véc-tơ điện 
 thế T chỉ có thành phần phát tuyến, chúng ta có phương 
 trình sau: 
 1
 ( × ) = − ( (T )) (12) 
   
 với Tn là thành phần pháp tuyến của véc-tơ T: T = .  
 Hình 1. Vùng vỏ mỏng dẫn điện 
 Phương trình (9) trở thành: 
 Chúng ta xem xét một vùng vỏ mỏng dẫn điện (, 
 ) 1
 có bề dày e và thể tích Ω. Γ là bề mặt trung bình như hình 1.  ⋅  (T ). dΓ = −jω.  . . . dΓ (13) 
     
 Biến thiên điện từ trường trong vùng dẫn được mô tả  
 bằng hệ phương trình Maxwell: Từ trường tại điểm P bất kỳ có thể viết dưới dạng: 
36 Tạp chí KHOA HỌC VÀ CÔNG NGHỆ ● Tập 56 - Số 3 (6/2020) Website: https://tapchikhcn.haui.edu.vn 
P-ISSN 1859-3585 E-ISSN 2615-9619 SCIENCE - TECHNOLOGY 
 (P) = (P) + (P) (14) 3. BÀI TOÁN ÁP DỤNG 
 Do thiếu các thiết bị để tiến hành thực nghiệm và đo 
 Với H0 là từ trường của nguồn ngoài, HJ là từ trường do 
dòng điện xoáy trong vùng dẫn vỏ mỏng gây ra. đếm kết quả thực tế, nên để kiểm chứng phương pháp 
 được phát triển trong mục 2, tác giả đã lựa chọn hai ví dụ 
 Áp dụng định luật Biot-Savart, chúng ta có: 
 kinh điển là các thiết bị có cấu trúc đối xứng trục (hình 3). 
 e  ×  Với các ví dụ này, chúng ta có thể sử dụng phương pháp 
 () =   dΓ (15) 
 4π  r FEM 2D để mô phỏng và tính toán. Phương pháp FEM 2D 
 với r là véc-tơ giữa điểm điểm lấy tích phân trên Γ và có số phần tử chia lưới không cần nhiều như trong mô hình 
điểm tính toán từ trường P. 3D, nên dễ dàng xác định nghiệm hội tụ và kết quả được 
 xem là giá trị chuẩn khi so sánh với các phương pháp khác. 
 Kết hợp các phương trình (13), (14), (15), chúng ta có hệ 
 Các thiết bị được mô phỏng trong mô hình 3D bởi phương 
phương trình cuối cùng: 
 pháp IDM đã trình bày trong bài báo. 
 1
 ⎧  w ⋅  (T )dΓ Mục đích của bài toán là xác định tổn thất joule trong 
 σ    
 ⎪  vùng dẫn dạng vỏ mỏng và phân bố dòng điện trên bề mặt 
 ⎪ e. μ  ×  vùng dẫn. 
 +jω.  w   dΓ ⋅ dΓ
 4π   r (16) 
 ⎨ z
 ⎪ = −jω. μ w. .. dΓ
 ⎪   
 ⎩  =  0
 Để giải hệ phương trình (16), phương pháp số được sử 
dụng bằng cách chia lưới bề mặt Γ thành n phần tử với giả R
thiết mật độ dòng điện J là hằng số trên mỗi phần tử. Gọi p x
 H e
là số nút của mạng lới. 0 y
 Giá trị véc-tơ điện thế được xác định dưới dạng: 
 
 T =  w (x, y, z)T (17) 
    
  Hình 2. Cầu rỗng dẫn điện 
 Chúng ta thu được hệ phương trình dưới dạng ma trận: 
 [] ⋅ [] + [s] ⋅ [] = [ ]
   (18) 
 [] = [] ⋅ []
 Hay là: R
  
 {[] + [s] ⋅ []} ⋅ [] = [] (19) 0 e
 H0
 Hệ phương trình (2) có p ẩn số. [A] là ma trận phần tử 
hữu hạn kích thước (p × p); [Bs] là ma trận biểu thị định luật 
Biot - Savart, nhận được từ công thức (17) với giá trị dòng 
điện xoáy đơn vị (p × 3n) ; [P] là ma trận (3n × p) và [h0] là 
véc-tơ kích thước p biểu thị thành phần pháp tuyến của Hình 3. Đĩa mỏng dẫn điện 
nguồn từ trường ngoài tại mỗi nút của mạng lưới. 3.1. Cầu rỗng dẫn điện 
 Các giá trị thành phần của ma trận [A], [Bs] và [h0] là: Ví dụ đầu tiên là một quả cầu rỗng với bề dày e = 2mm 
 1 bán kính trong là R = 0,1m, đặt trong một từ trường đều 
 (i, k) = w ⋅ wdΓ (20) 
 σ  H0 = [0 0 1] (A/m) với tần số f = 50Hz. Độ dẫn điện của quả 
 cầu là 6x107S/m (hình 2). Với tần số f = 50Hz, độ sâu bề mặt 
 e. μ  × 
  (i, k) = jω.  w  dΓ ⋅  dΓ (21)  = 9mm thoả mãn điều điện  >> e. Kết quả tính toán tổn 
  4π  r 
   thất Joule bằng phương pháp FEM 2D hội tụ ở 20.000 phần 
 tử chia lưới và có giá trị là 1,14x10-6 (W). 
 (i) = −jω. μ w. .. dΓ (22) Hình 4 là kết quả tính toán tổn thất Joule bởi phương 
  pháp IDM và sai số so với giá trị chuẩn theo số phần tử chia 
 với  là véc-tơ đơn vị của dòng điện xoáy của phần tử k. lưới. Chúng ta nhận thấy, phương pháp được phát triển cho 
 Tác giả đã thiết lập công cụ tính toán trong môi trường kết quả tương tự so với FEM 2D. Chỉ cần chia lưới thành 
Matlab. Trong phân tiếp theo sẽ trình bày kiểm chứng 4800 phần tử thì đã đạt được kết quả gần chính xác với sai 
phương pháp cũng như phân tích đánh giá khả năng áp số 0,3%. Phương pháp này có khả năng mô phỏng điện từ 
dụng, các hướng phát triển của nghiên cứu. các vùng dẫn dạng vỏ mỏng. 
 Website: https://tapchikhcn.haui.edu.vn Vol. 56 - No. 3 (June 2020) ● Journal of SCIENCE & TECHNOLOGY 37
 KHOA H ỌC CÔNG NGHỆ P - ISSN 1859 - 3585 E - ISSN 2615 - 961 9 
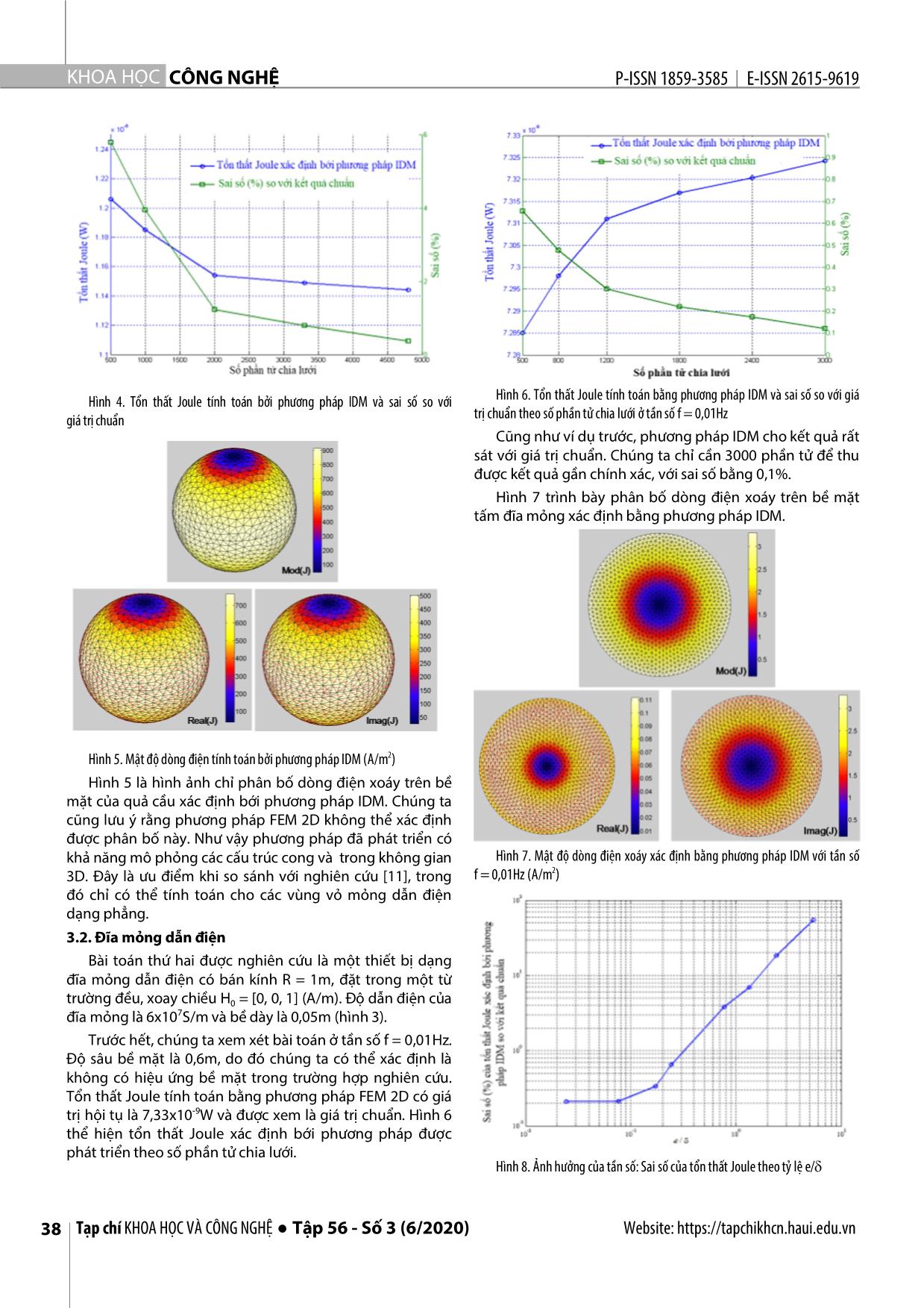
 Hình 4. Tổn thất Joule tính toán bởi phương pháp IDM và sai số so với Hình 6. Tổn thất Joule tính toán bằng phương pháp IDM và sai số so với giá 
 giá trị chuẩn trị chuẩn theo số phần tử chia lưới ở tần số f = 0,01Hz 
 Cũng như ví dụ trước, phương pháp IDM cho kết quả rất 
 sát với giá trị chuẩn. Chúng ta chỉ cần 3000 phần tử để thu 
 được kết quả gần chính xác, với sai số bằng 0,1%. 
 Hình 7 trình bày phân bố dòng điện xoáy trên bề mặt 
 tấm đĩa mỏng xác định bằng phương pháp IDM. 
 Hình 5. Mật độ dòng điện tính toán bởi phương pháp IDM (A/m2) 
 Hình 5 là hình ảnh chỉ phân bố dòng điện xoáy trên bề 
 mặt của quả cầu xác định bới phương pháp IDM. Chúng ta 
 cũng lưu ý rằng phương pháp FEM 2D không thể xác định 
 được phân bố này. Như vậy phương pháp đã phát triển có 
 khả năng mô phỏng các cấu trúc cong và trong không gian Hình 7. Mật độ dòng điện xoáy xác định bằng phương pháp IDM với tần số 
 3D. Đây là ưu điểm khi so sánh với nghiên cứu [11], trong f = 0,01Hz (A/m2) 
 đó chỉ có thể tính toán cho các vùng vỏ mỏng dẫn điện 
 dạng phẳng. 
 3.2. Đĩa mỏng dẫn điện 
 Bài toán thứ hai được nghiên cứu là một thiết bị dạng 
 đĩa mỏng dẫn điện có bán kính R = 1m, đặt trong một từ 
 trường đều, xoay chiều H0 = [0, 0, 1] (A/m). Độ dẫn điện của 
 đĩa mỏng là 6x107S/m và bề dày là 0,05m (hình 3). 
 Trước hết, chúng ta xem xét bài toán ở tần số f = 0,01Hz. 
 Độ sâu bề mặt là 0,6m, do đó chúng ta có thể xác định là 
 không có hiệu ứng bề mặt trong trường hợp nghiên cứu. 
 Tổn thất Joule tính toán bằng phương pháp FEM 2D có giá 
 trị hội tụ là 7,33x10-9W và được xem là giá trị chuẩn. Hình 6 
 thể hiện tổn thất Joule xác định bới phương pháp được 
 phát triển theo số phần tử chia lưới. 
 Hình 8. Ảnh hưởng của tần số: Sai số của tổn thất Joule theo tỷ lệ e/ 
38 Tạp chí KHOA HỌC VÀ CÔNG NGHỆ ● Tập 56 - Số 3 (6/2020) Website: https://tapchikhcn.haui.edu.vn 
P-ISSN 1859-3585 E-ISSN 2615-9619 SCIENCE - TECHNOLOGY 
 Để đánh giá thêm về khả năng tính toán và phạm vi áp [10]. K. Ishibashi, Z. Andjelic, Y. Takahashi, T. Takamatsu, K. Tsuzaki, S. 
dụng của phương pháp IDM, tác giả đã tiến hành tính toán Wakao, K. Fujiwara, Y. Ishihara, 2012. Some Treatments of Fictitious Volume 
mô phỏng với nhiều tần số khác nhau. Khi tần số tăng dần, Charges in Nonlinear Magnetostatic Analysis by BIE. IEEE Transaction on 
độ sâu bề bề mặt trở nên bé dần. Phương pháp được phát Magnetics, vol. 48, no. 2, pp. 463-466. 
triển trong bài báo dựa trên giả thiết dòng điện không đổi [11]. S.J. Salon, B. Mathewson and S. Uda, 1983. An Integro-Differential 
theo bề dày của vùng vỏ mỏng sẽ không còn chính xác bởi Approach to Eddy Currents in Thin Plates. IEEE Transactions on Magnetics, 
vì điều kiện  >> e không được thoả mãn. Để phương pháp Vol.Mag-19, No.6. 
IDM cho kết quả chấp nhận được (sai số bé hơn 2% so với 
giá trị chuẩn), hình 8 chỉ ra rằng tỷ số giữa bề dày đĩa mỏng 
 AUTHOR INFORMATION 
và độ sâu bề mặt phải nhỏ hơn 0,5 (e/ < 0,5). 
 Le Duc Tung 
4. KẾT LUẬN 
 School of Electrical Engineering, Hanoi Unviversity of Science and Technology 
 Bài báo đã giới thiệu, phát triển công thức lai, kết hợp 
giữa phương trình tích phân và vi phân để giải bài toán 
điện từ có cấu trúc dạng vỏ mỏng dẫn điện trong không 
gian 3D. Phương pháp được phát triển chỉ cần chia lưới bề 
mặt trung bình của vùng vỏ mỏng, giúp giảm thời gian 
cũng như khối lượng tính toán. Các kết quả tính toán, mô 
phỏng cũng được so sánh với kết quả chuẩn đạt được từ 
phần mềm công nghiệp dựa trên phương pháp phần tử 
hữu hạn 2D. Tuy nhiên, phương pháp còn có sai số khi hiệu 
ứng bề mặt trong vùng dẫn điện lớn (e >> ). Điểm giới hạn 
này sẽ được đầu tư ở các nghiên cứu tiếp theo. 
 LỜI CẢM ƠN 
 Nghiên cứu này được tài trợ bởi Bộ Giáo dục và Đào tạo 
trong đề tài mã số B2018-BKA-11-CtrVL. 
 TÀI LIỆU THAM KHẢO 
 [1]. Salon, Sheppard, and M. V. K. Chari, 1999. Numerical methods in 
electromagnetism. Academic Press. 
 [2]. G. Meunier, 2008. The Finite Element Method for Electromagnetic 
Modeling. Wiley. 
 [3]. Maxwell ANSYS. Canonsburg, USA. Available: www.ansys.com 
 [4]. Flux Cedrat. Meylan, France [Online]. Available: www.cedrat.com 
 [5]. C. Hoer, C. Love, 1965. Exact Inductance Equations for Rectangular 
Conductors With Applications to More Complicated Geometries. Journal of 
Research of the national Bureau of Standards-C. Engineering and 
Instrumentation, Vol. 69C, No. 2, 127-137, 1965. 
 [6]. De Camillis L., Ferranti F., Antonini G., Vande Ginste D., De Zutter D., 
2012. Parameterized Partial Element Equivalent Circuit Method for Sensitivity 
Analysis of Multiport Systems. IEEE Transactions on Components, Packaging and 
Manufacturing Technology, Vol.2, No.2, pp. 248-255. 
 [7]. T. Le-Duc, G. Meunier, O. Chadebec, J-M. Guichon and J.P.A Bastos, 
2013. General Integral Formulation for the 3D Thin Shell Modeling. IEEE 
Transactions on Magnetics, Vol. 49, No. 5, pp. 1989-1992. 
 [8]. T. Le-Duc, O. Chadebec, J-M. Guichon, G. Meunier and Y. Lembeye, 2013. 
Coupling between Partial Element Equivalent Circuit Method and Magnetic Moment 
Method. The International Journal for Computation and Mathematics in Electrical 
and Electronic Engineering (COMPEL), Vol. 32, No. 1, pp. 383-395. 
 [9]. K. Ishibashi, Z. Andjelic, D. Pusch, 2010. Nonlinear Eddy Current Analysis 
by BEM Minimum Order Formulation. IEEE Transaction on Magnetics, vol. 46, no. 
8, pp. 3085-3088. 
 Website: https://tapchikhcn.haui.edu.vn Vol. 56 - No. 3 (June 2020) ● Journal of SCIENCE & TECHNOLOGY 39