Phân tích dao động mảnh vỏ cầu thoải có cơ tính biến thiên trong môi trường nhiệt độ bằng phương pháp phần tử hữu hạn

../../../../../LUAN AN_Huan/KET QUA 
SO/KetQuaSo_LuanAn/Code_KIEMCHUNG_LA_HUAN/KQ_K
C_Dao dong rieng_Tab4_Shen 2015.xlsx - 
RANGE!_ENREF_93 (Shen & cs., 2015) 
6.8414 16.7251 16.7137 25.8402 
Bài báo 6.9018 16.4971 16.5228 25.5174 
Sai lệch (%) 0.88 1.38 1.16 1.27 
Nhận xét: Bâng so sánh cho thấy sai lệch giữa kết quâ công bố bởi (Shen, Chen & cs. 2015) theo mô hình giâi 
tích dựa trên lý thuyết biến däng cắt bậc cao và kết quâ tính bằng mô hình PTHH của bài báo là không đáng kể 
(lớn nhất là 1.73%). Từ đó cho thấy độ tin cậy của mô hình và kết quâ số mà bài báo đã thiết lập. 
Dương Thành Huân 
1007 
3.2. Kết quả khảo sát 
3.2.1. Bài toán dao động riêng 
a. Ví dụ 1 - Ảnh hưởng của chî số tỷ lệ thể tích p 
Xét mânh vó cæu thoâi FGM 
(Si3N4/SUS304), có h = 0.01 m, a/h = 20; a/R = 
1/5 với ba loäi điều kiện biên là bốn cänh đều là 
khớp (SSSS); hai cänh khớp, hai cänh ngàm 
(SCSC) và bốn cänh ngàm (CCCC). Giâ thiết 
truyền nhiệt phi tuyến với Tm = 300 K và Tc = 500 
K. Kết quâ được trình bày trong bâng 3. 
b. Ví dụ 2 - Ảnh hưởng của tỷ số a/h 
Mânh vó cæu thoâi FGM (Si3N4/ SUS304) 
trong ví dụ này có chî số tỷ lệ thể tích p = 2, h = 
0.01 m, a = 1.0 m; R = 5 m. Ba loäi điều kiện 
biên được xem xét là SSSS, SCSC và CCCC. 
Nhiệt độ được truyền phi tuyến với Tm = 300 K, 
Tc = 400 K. 
Tæn số dao động riêng không thứ nguyên 
được tính toán theo công thức 0
2
0
100. .h
E
 
((Wattanasakulpong & Chaikittiratana, 2015)), 
trong đò 0 và E0 là các giá trð tham chiếu của c 
và Ec täi T0 = 300 K. Ảnh hưởng của tỷ số a/h 
đến tæn số dao động riêng của vó được biểu diễn 
trên hình 2. 
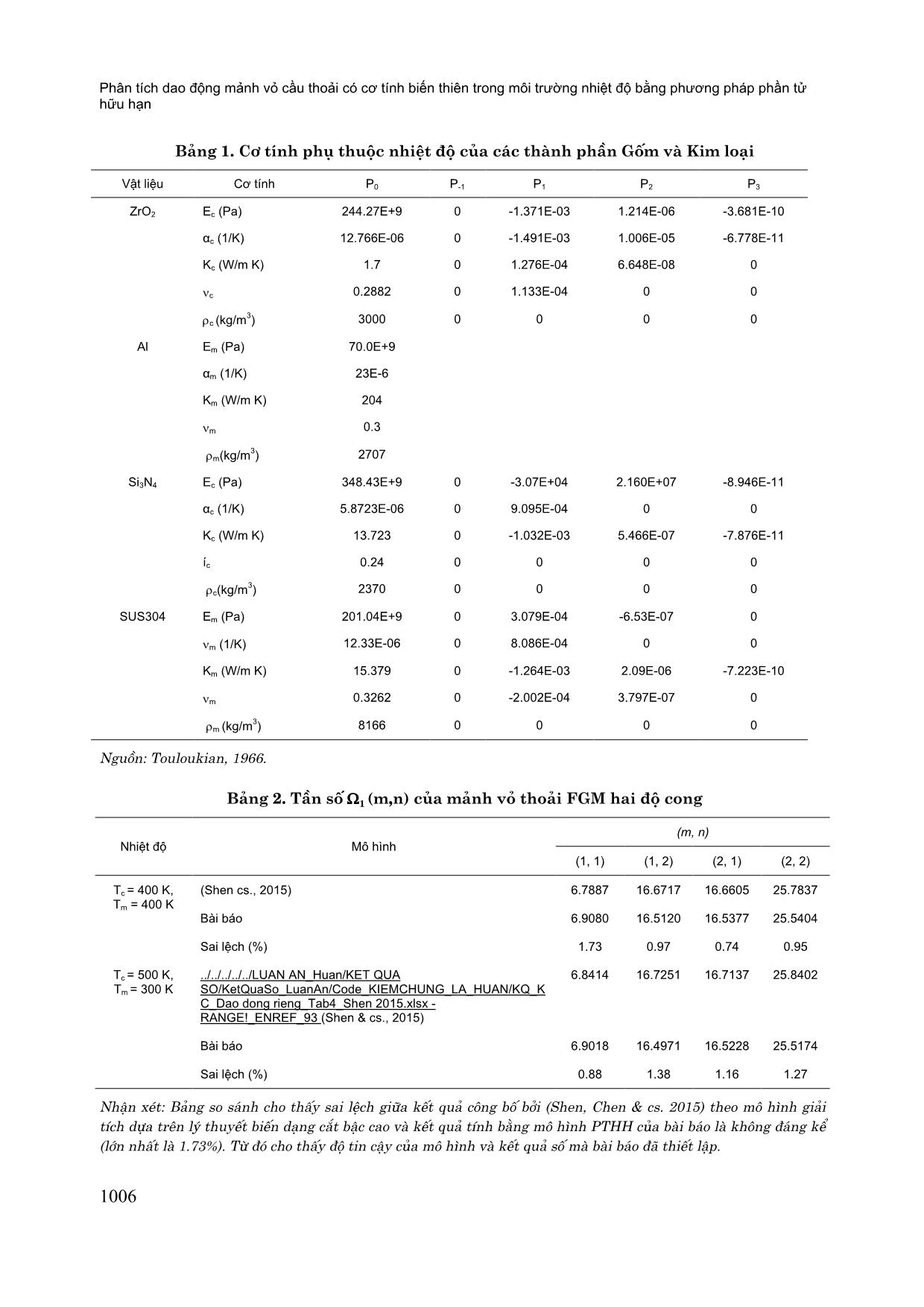
Nhận xét: Kết quâ tính bằng đáp ứng chuyển vð theo mô hình PTHH của bài báo cũng rất gần khi so với kết quâ 
tính theo mô hình giâi tích của Reddy. Điều này một lần nữa khẳng đðnh thuật toán và mô hình của bài báo 
thiết lập là có độ tin cậy. 
Hình 1. Đáp ứng chuyển vị tại điểm chính giữa tấm FGM (a/2, b/2) 
Bảng 3. Ảnh hưởng của chỉ số tỷ lệ thể tích p đến Ω1 
Điều kiện biên 
Chỉ số tỉ lệ thể tích p 
p = 0 p = 0.5 p = 1 p = 2 p = 5 
SSSS 14.7688 10.2388 9.0591 8.2595 7.6984 
SCSC 20.8964 14.4588 12.7433 11.5401 10.6412 
CCCC 26.2197 18.1488 15.9694 14.4151 13.2258 
Nhận xét: Giá trð tần số dao động riêng cơ bân của vỏ với câ ba trường hợp điều kiện biên được khâo sát đều 
giâm khi tî số tî lệ thể tích p tăng. Điều này là hoàn toàn phù hợp với qui luật của vật liệu: khi p tăng thì đồng 
nghïa với việc hàm lượng gốm (ceramic) trong vật liệu giâm và hàm lượng kim loäi (metal) tăng và do đó vỏ trở 
lên mềm hơn. 
Phân tích dao động mảnh vỏ cầu thoải có cơ tính biến thiên trong môi trường nhiệt độ bằng phương pháp phần tử 
hữu hạn 
1008 
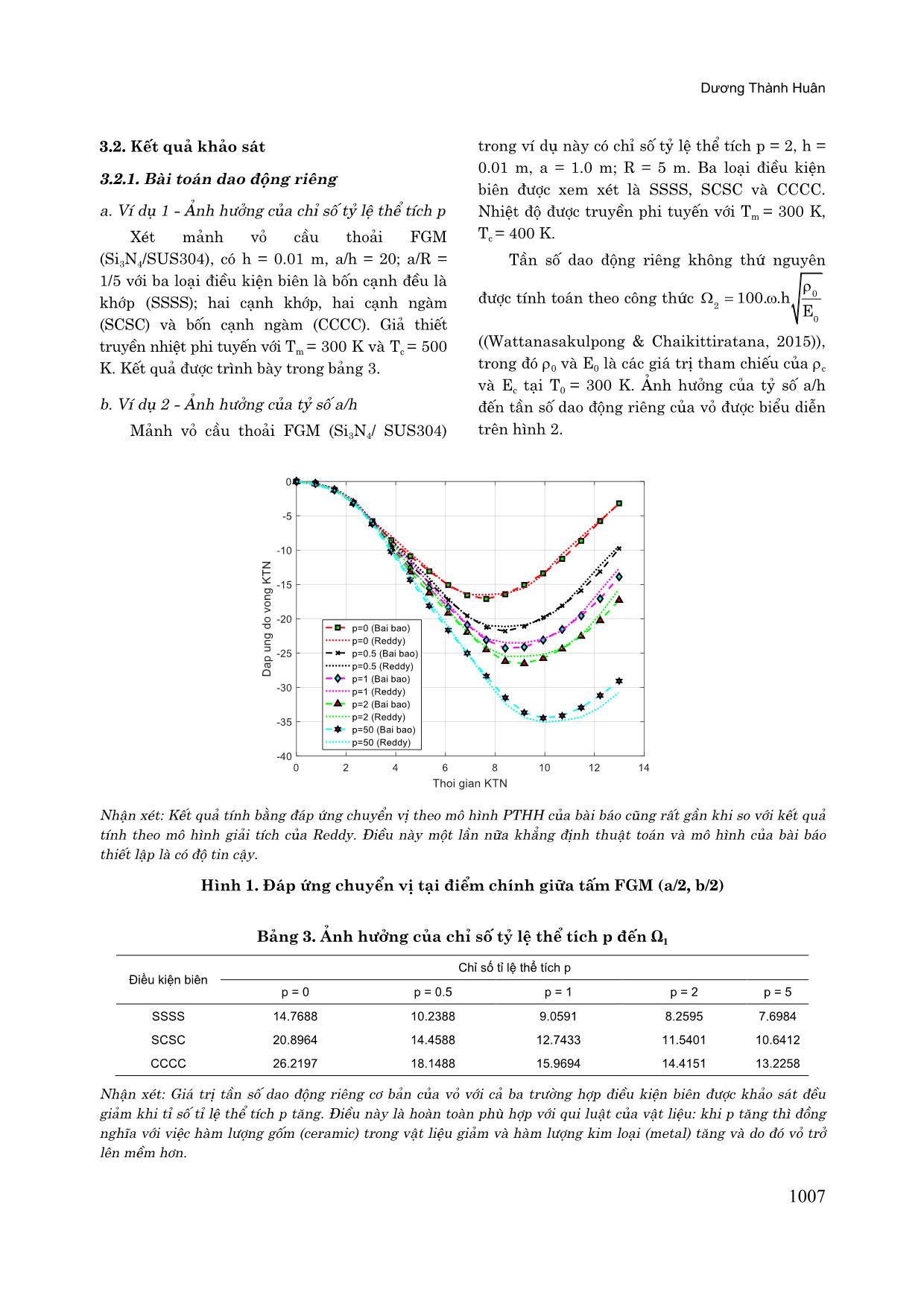
Nhận xét: Khi tỷ số a/h tăng, các vỏ trở nên mỏng hơn và do đó độ cứng của vỏ giâm, điều này được phân ánh 
thông qua tần số dao động riêng Ω2 của các vỏ đều giâm khi tî số a/h tăng. Độ giâm của Ω2 lớn khi tỷ số a/h tăng 
từ 10 đến 30, sau đó tốc độ giâm nhỏ dần, khi tỷ số a/h lớn hơn 40 thì tần số Ω2 thay đổi rất nhỏ. 
Hình 3. Ảnh hưởng của tỷ số a/h đến Ω2 của mảnh vỏ cầu thoải FGM 
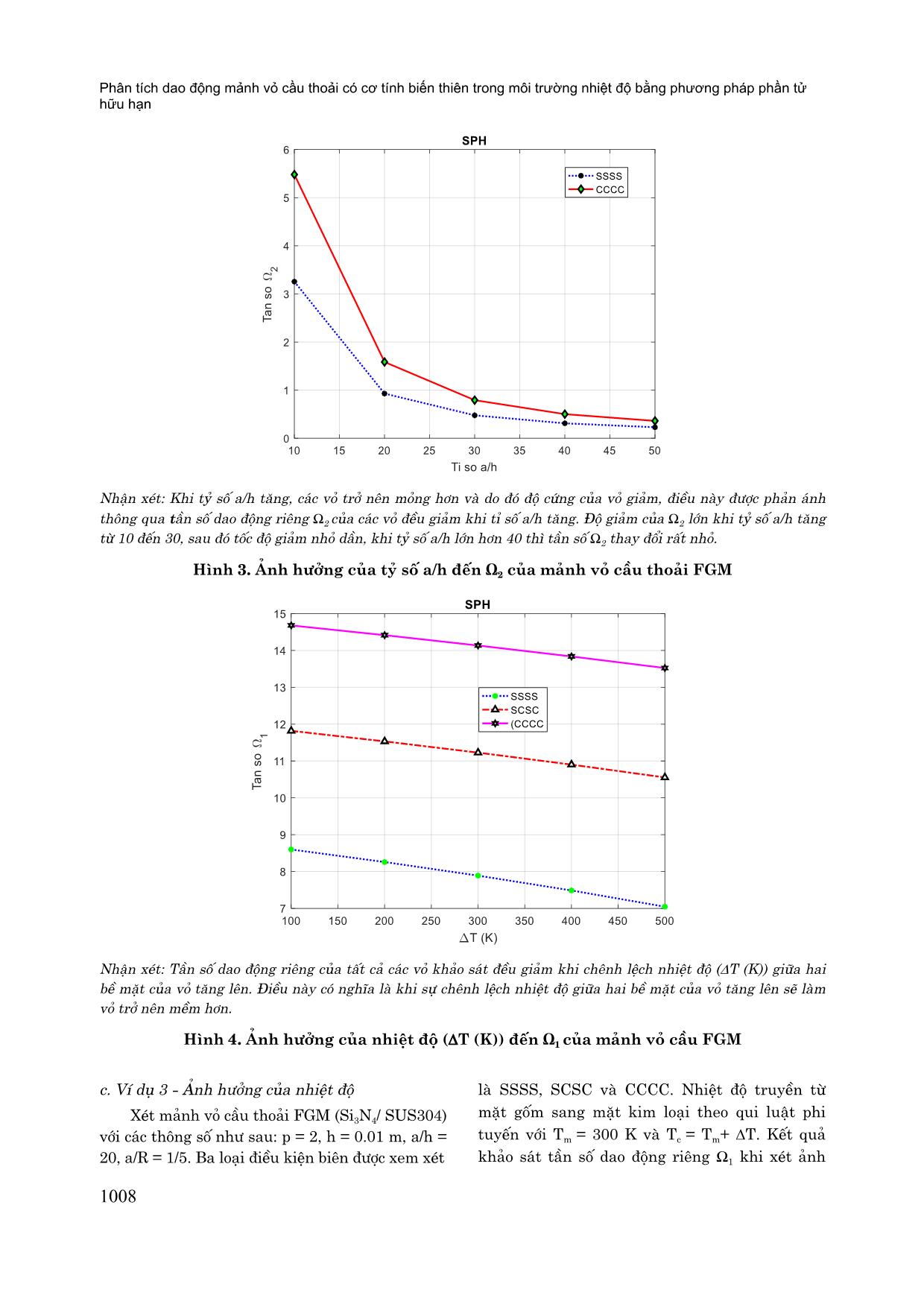
Nhận xét: Tần số dao động riêng của tất câ các vỏ khâo sát đều giâm khi chênh lệch nhiệt độ ( T (K)) giữa hai 
bề mặt của vỏ tăng lên. Điều này có nghïa là khi sự chênh lệch nhiệt độ giữa hai bề mặt của vỏ tăng lên sẽ làm 
vỏ trở nên mềm hơn. 
Hình 4. Ảnh hưởng của nhiệt độ ( T (K)) đến Ω1 của mảnh vỏ cầu FGM 
c. Ví dụ 3 - Ảnh hưởng của nhiệt độ 
Xét mânh vó cæu thoâi FGM (Si3N4/ SUS304) 
với các thông số như sau: p = 2, h = 0.01 m, a/h = 
20, a/R = 1/5. Ba loäi điều kiện biên được xem xét 
là SSSS, SCSC và CCCC. Nhiệt độ truyền từ 
mặt gốm sang mặt kim loäi theo qui luật phi 
tuyến với Tm = 300 K và Tc = Tm+ T. Kết quâ 
khâo sát tæn số dao động riêng Ω1 khi xét ânh 
Dương Thành Huân 
1009 
hưởng của sự thay đổi nhiệt độ giữa hai bề mặt 
kết cçu được thể hiện trên hình 4. 
3.2.2. Bài toán dao động cưỡng bức 
Trong phæn này, ânh hưởng của các tham 
số vật liệu, tham số hình học, nhiệt độ và hệ số 
cân đến đáp ứng chuyển vð của vó FGM được 
khâo sát. Hai loäi tâi trọng được xét là: tâi 
trọng xung và tâi trọng điều hòa có däng F(t) = 
P0.P(t). Với tâi trọng xung: P(t) = {1, 0 ≤ t}; tâi 
trọng điều hòa: P(t) = sin (Ωt). Trong đò: P0 là 
biên độ của lực cưỡng bức; Ω là tæn số dao động 
của lực cưỡng bức. Đáp ứng chuyển vð trong tçt 
câ các trường hợp khâo sát trong bài báo là đáp 
ứng của điểm chính giữa vó Km (a/2, b/2). 
a. Ví dụ 1 - Mânh vỏ cầu thoâi FGM chðu tâi 
trọng xung 
Xét mânh vó cæu thoâi FGM (Si3N4/ 
SUS304) với các thông số như sau: h = 0.01 m, 
R/a = 5, tựa bân là bốn cänh SSSS. Nhiệt 
truyền phi tuyến Tm = 300 K, Tc = 500 K, tâi 
trọng xung phân bố đều q0 = 10
6 (Pa). Ảnh 
hưởng của chî số tî lệ thể tích p, tỷ số a/h và tî 
lệ cân đến đáp ứng chuyển vð của các vó (Hình 
5, 6, 7). 
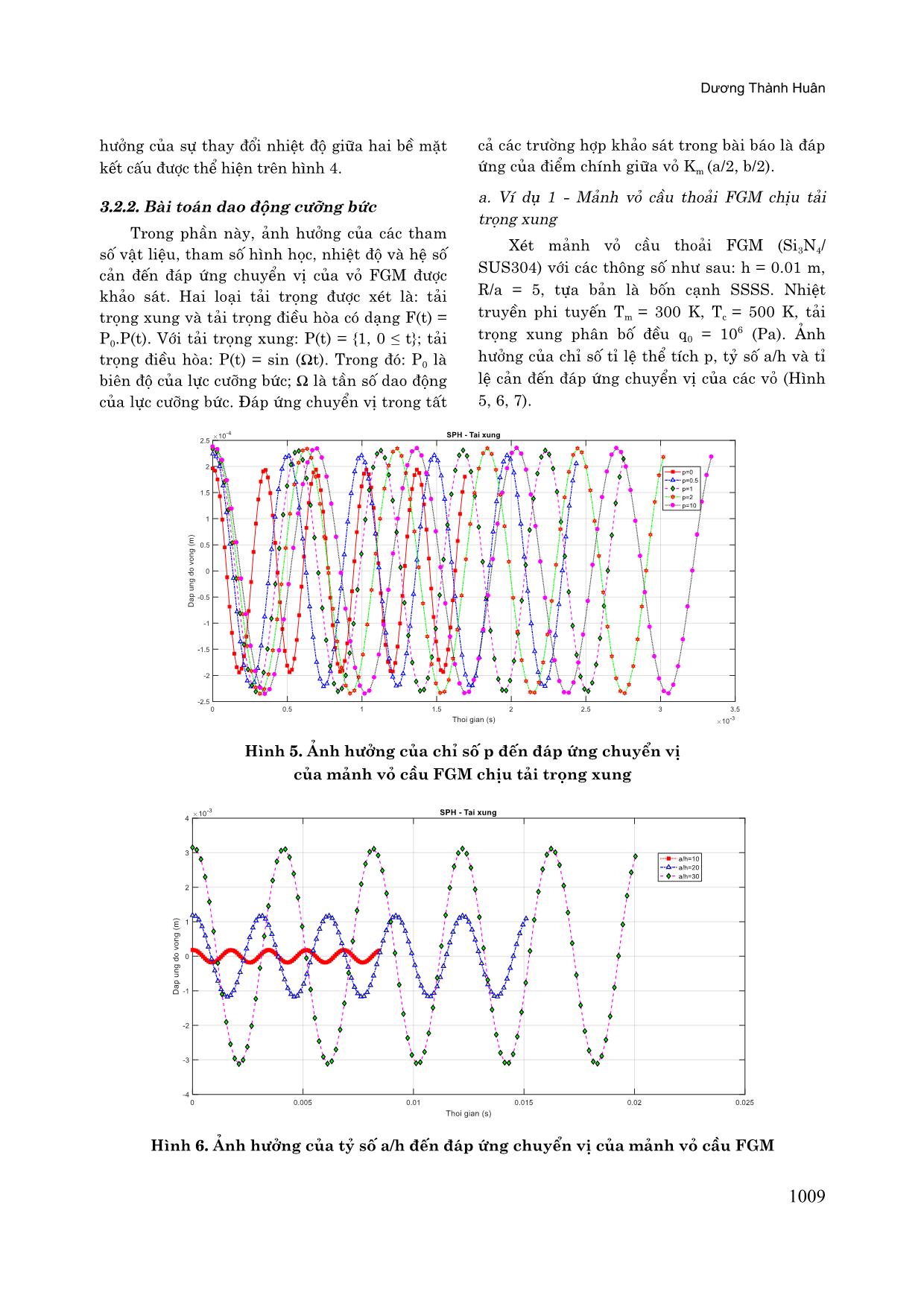
Hình 5. Ảnh hưởng của chỉ số p đến đáp ứng chuyển vị 
của mảnh vỏ cầu FGM chịu tải trọng xung 
Hình 6. Ảnh hưởng của tỷ số a/h đến đáp ứng chuyển vị của mảnh vỏ cầu FGM 
Phân tích dao động mảnh vỏ cầu thoải có cơ tính biến thiên trong môi trường nhiệt độ bằng phương pháp phần tử 
hữu hạn 
1010 
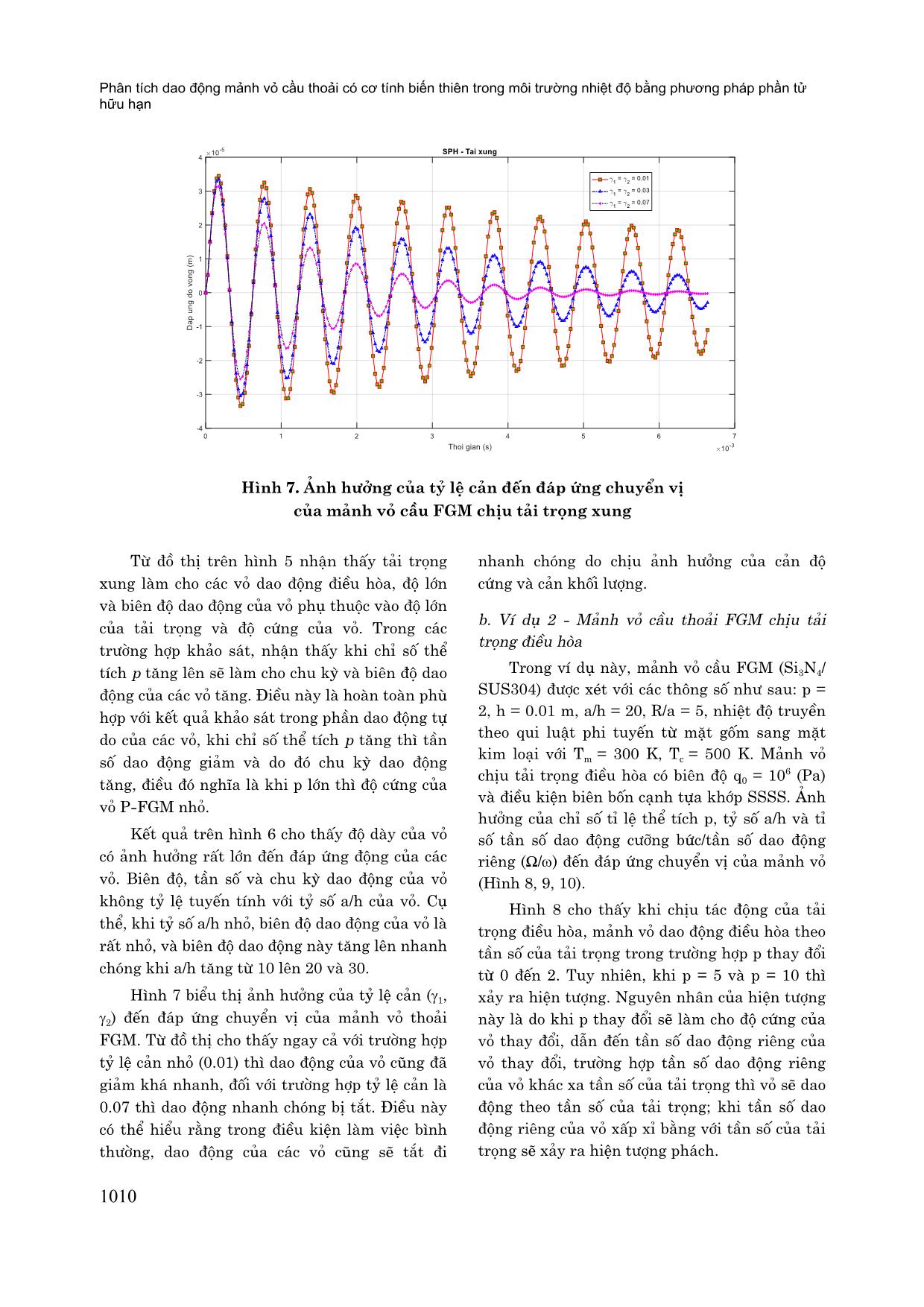
Hình 7. Ảnh hưởng của tỷ lệ cản đến đáp ứng chuyển vị 
của mảnh vỏ cầu FGM chịu tải trọng xung 
Từ đồ thð trên hình 5 nhận thçy tâi trọng 
xung làm cho các vó dao động điều hña, độ lớn 
và biên độ dao động của vó phụ thuộc vào độ lớn 
của tâi trọng và độ cứng của vó. Trong các 
trường hợp khâo sát, nhận thçy khi chî số thể 
tích p tăng lên sẽ làm cho chu kỳ và biên độ dao 
động của các vó tăng. Điều này là hoàn toàn phù 
hợp với kết quâ khâo sát trong phæn dao động tự 
do của các vó, khi chî số thể tích p tăng thì tæn 
số dao động giâm và do đò chu kỳ dao động 
tăng, điều đò nghïa là khi p lớn thì độ cứng của 
vó P-FGM nhó. 
Kết quâ trên hình 6 cho thçy độ dày của vó 
có ânh hưởng rçt lớn đến đáp ứng động của các 
vó. Biên độ, tæn số và chu kỳ dao động của vó 
không tỷ lệ tuyến tính với tỷ số a/h của vó. Cụ 
thể, khi tỷ số a/h nhó, biên độ dao động của vó là 
rçt nhó, và biên độ dao động này tăng lên nhanh 
chòng khi a/h tăng từ 10 lên 20 và 30. 
Hình 7 biểu thð ânh hưởng của tỷ lệ cân (1, 
2) đến đáp ứng chuyển vð của mânh vó thoâi 
FGM. Từ đồ thð cho thçy ngay câ với trường hợp 
tỷ lệ cân nhó (0.01) thì dao động của vó cũng đã 
giâm khá nhanh, đối với trường hợp tỷ lệ cân là 
0.07 thì dao động nhanh chóng bð tắt. Điều này 
có thể hiểu rằng trong điều kiện làm việc bình 
thường, dao động của các vó cũng sẽ tắt đi 
nhanh chóng do chðu ânh hưởng của cân độ 
cứng và cân khối lượng. 
b. Ví dụ 2 - Mânh vỏ cầu thoâi FGM chðu tâi 
trọng điều hòa 
Trong ví dụ này, mânh vó cæu FGM (Si3N4/ 
SUS304) được xét với các thông số như sau: p = 
2, h = 0.01 m, a/h = 20, R/a = 5, nhiệt độ truyền 
theo qui luật phi tuyến từ mặt gốm sang mặt 
kim loäi với Tm = 300 K, Tc = 500 K. Mânh vó 
chðu tâi trọng điều hña cò biên độ q0 = 10
6 (Pa) 
và điều kiện biên bốn cänh tựa khớp SSSS. Ảnh 
hưởng của chî số tî lệ thể tích p, tỷ số a/h và tî 
số tæn số dao động cưỡng bức/tæn số dao động 
riêng (Ω/) đến đáp ứng chuyển vð của mânh vó 
(Hình 8, 9, 10). 
Hình 8 cho thçy khi chðu tác động của tâi 
trọng điều hòa, mânh vó dao động điều hòa theo 
tæn số của tâi trọng trong trường hợp p thay đổi 
từ 0 đến 2. Tuy nhiên, khi p = 5 và p = 10 thì 
xây ra hiện tượng. Nguyên nhân của hiện tượng 
này là do khi p thay đổi sẽ làm cho độ cứng của 
vó thay đổi, dẫn đến tæn số dao động riêng của 
vó thay đổi, trường hợp tæn số dao động riêng 
của vó khác xa tæn số của tâi trọng thì vó sẽ dao 
động theo tæn số của tâi trọng; khi tæn số dao 
động riêng của vó xçp xî bằng với tæn số của tâi 
trọng sẽ xây ra hiện tượng phách. 
Dương Thành Huân 
1011 
Hình 8. Ảnh hưởng của chỉ số p đến đáp ứng động 
của mảnh vỏ cầu FGM chịu tải trọng điều hòa 
Hình 9. Ảnh hưởng của tỷ số a/h đến đáp ứng động 
của mảnh vỏ cầu FGM chịu tải trọng điều hòa 
Hình 10. Ảnh hưởng của tỉ số Ω/ đến đáp ứng động 
của mảnh vỏ cầu FGM chịu tải trọng điều hòa 
Phân tích dao động mảnh vỏ cầu thoải có cơ tính biến thiên trong môi trường nhiệt độ bằng phương pháp phần tử 
hữu hạn 
1012 
Hình 9 cho thçy khi tỷ số a/h thay đổi thì 
biên độ dao động của mânh vó thay đổi một cách 
nhanh chòng, điều này một læn nữa khẳng đðnh 
tỷ số a/h là tham số ânh hưởng rçt lớn đến khâ 
năng chðu lực của các vó FGM. Nói cách khác, 
độ dày là yếu tố rçt quan trọng quyết đðnh độ 
cứng của vó. 
Kết quâ trên hình 10 cho thçy khi vó chðu 
tâi trọng điều hòa có tæn số khác xa so với tæn số 
dao động riêng của nó thì vó sẽ dao động theo 
tâi trọng ngoài, độ lớn của biên độ dao động phụ 
thuộc vào độ cứng của vó và biên độ của tâi 
trọng. Khi tæn số dao động của tâi trọng gæn với 
tæn số dao động riêng của vó thì xây ra hiện 
tượng phách và khi tæn số của tâi trọng bằng với 
tæn số dao động riêng của vó thì xây ra hiện 
tượng cộng hưởng. 
4. KẾT LUẬN 
Mô hình phæn tử hữu hän sử dụng phæn tử 
3D suy biến đã được thiết lập trong bài báo này 
để phån tích dao động tự do và đáp ứng động 
của mânh vó cæu thoâi FGM trong môi trường 
nhiệt độ. Với giâ thiết nhiệt độ được truyền qua 
chiều dày vó theo các quy luật hằng số, bậc nhçt 
và phi tuyến, bài báo đã khâo sát ânh hưởng của 
các tham số vật liệu, kích thước hình học và tâi 
trọng tác động đến đáp ứng chuyển vð của vó với 
một số điều kiện biên thông dụng. Kết quâ kiểm 
chứng cho thçy sự chính xác của mô hình và 
chương trình tính. Qua kết quâ khâo sát có thể 
nhận thçy đáp ứng động của vó FGM phụ thuộc 
nhiều vào độ dày của vó, điều kiện biên, sự 
chênh lệch nhiệt độ giữa hai bề mặt và tính chçt 
của tâi trọng tác động. 
TÀI LIỆU THAM KHẢO 
Ahmad S., Irons B.M. Zienkiewicz O. (1970). Analysis 
of thick and thin shell structures by curved finite 
elements. International Journal for Numerical 
Methods in Engineering. 2(3): 419-451. 
Bich D.H., Ninh D.G. & Thinh T.I. (2016). Non-linear 
buckling analysis of FGM toroidal shell segments 
filled inside by an elastic medium under external 
pressure loads including temperature effects. 
Composites Part B: Engineering. 87: 75-91. 
Bich D.H. & Van Dung D. (2012). Nonlinear static and 
dynamic buckling analysis of functionally graded 
shallow spherical shells including temperature 
effects. Composite Structures. 94(9): 2952-2960. 
Bich D.H. & Van Tung H. (2011). Non-linear 
axisymmetric response of functionally graded 
shallow spherical shells under uniform external 
pressure including temperature effects. 
International Journal of Non-Linear Mechanics. 
46(9): 1195-1204. 
Duc N.D. & Cong P.H. (2013). Nonlinear postbuckling 
of symmetric S-FGM plates resting on elastic 
foundations using higher order shear deformation 
plate theory in thermal environments. Composite 
Structures. 100: 566-574. 
Duc N.D. & Quan T.Q. (2013). Nonlinear postbuckling 
of imperfect eccentrically stiffened P-FGM double 
curved thin shallow shells on elastic foundations in 
thermal environments. Composite Structures. 106: 
590-600. 
Duc N.D. & Van Tung H. (2011). Mechanical and 
thermal postbuckling of higher order shear 
deformable functionally graded plates on elastic 
foundations. Composite Structures. 93(11): 2874-
2881. 
Haddadpour H., Mahmoudkhani S. & Navazi H. 
(2007). Free vibration analysis of functionally 
graded cylindrical shells including thermal effects. 
Thin-walled structures. 45(6): 591-599. 
Javaheri R. & M. Eslami (2002). Thermal buckling of 
functionally graded plates based on higher order 
theory. Journal of thermal stresses. 25(7): 603-625. 
Jooybar N., Malekzadeh P., Fiouz A. & Vaghefi M. 
(2016). Thermal effect on free vibration of 
functionally graded truncated conical shell panels. 
Thin-Walled Structures. 103: 45-61. 
Kadoli R. & Ganesan N. (2006). Buckling and free 
vibration analysis of functionally graded 
cylindrical shells subjected to a temperature-
specified boundary condition. Journal of Sound 
and Vibration. 289(3): 450-480. 
Kandasamy R., Dimitri R. & Tornabene F. (2016). 
Numerical study on the free vibration and thermal 
buckling behavior of moderately thick functionally 
graded structures in thermal environments. 
Composite Structures. 157: 207-221. 
Malekzadeh P., Fiouz A. & Sobhrouyan M. (2012). 
Three-dimensional free vibration of functionally 
graded truncated conical shells subjected to 
thermal environment. International Journal of 
Pressure Vessels and Piping. 89: 210-221. 
Malekzadeh P. & Heydarpour Y. (2012). Free vibration 
analysis of rotating functionally graded cylindrical 
shells in thermal environment. Composite 
Structures. 94(9): 2971-2981. 
Dương Thành Huân 
1013 
Ninh D.G. & Bich D.H. (2016). Nonlinear buckling of 
eccentrically stiffened functionally graded toroidal 
shell segments under torsional load surrounded by 
elastic foundation in thermal environment. 
Mechanics Research Communications. 72: 1-15. 
Pradyumna S. & Bandyopadhyay J. (2010). Free 
vibration and buckling of functionally graded shell 
panels in thermal environments. International 
Journal of Structural Stability and Dynamics. 
10(05): 1031-1053. 
Praveen G. & Reddy J.(1998). Nonlinear transient 
thermoelastic analysis of functionally graded 
ceramic-metal plates. International Journal of 
Solids and Structures. 35(33): 4457-4476. 
Reddy J. (2000). Analysis of functionally graded plates. 
International Journal for numerical methods in 
engineering. 47(1‐3): 663-684. 
Shen H.S., Chen X., Guo L., Wu L. & Huang X.L. 
(2015). Nonlinear vibration of FGM doubly curved 
panels resting on elastic foundations in thermal 
environments. Aerospace Science and Technology. 
47: 434-446. 
Sheng G. & Wang X. (2008). Thermal vibration, 
buckling and dynamic stability of functionally 
graded cylindrical shells embedded in an elastic 
medium. Journal of Reinforced Plastics and 
Composites. 27(2): 117-134. 
Touloukian Y.S. (1966). Thermophysical properties of 
high temperature solid materials, Thermophysical 
and Electronic Properties Information Analysis 
Center Lafayette In. 2 
Tùng Hoàng Văn Tùng (2011). Ổn định đàn hồi của 
tấm và vỏ composite có cơ tính biến đổi Luận án 
Tiến sĩ Cơ học, Trường Đại học Khoa học Tự 
nhiên - Đại học Quốc Gia Hà Nội. 
Van Tung H. & Duc N.D. (2010). Nonlinear analysis of 
stability for functionally graded plates under 
mechanical and thermal loads. Composite 
Structures. 92(5): 1184-1191. 
Van Tung H. & Duc N.D. (2014). Nonlinear response 
of shear deformable FGM curved panels resting on 
elastic foundations and subjected to mechanical 
and thermal loading conditions. Applied 
Mathematical Modelling. 38(11): 2848-2866. 
Wattanasakulpong N. & Chaikittiratana A. (2015). An 
analytical investigation on free vibration of FGM 
doubly curved shallow shells with stiffeners under 
thermal environment. Aerospace Science and 
Technology. 40: 181-190.