Parametric blind - deconvolution method to remove image artifacts in wavefront coding imaging systems
Since 1995, an asymmetrical cubic phase mask was firstly reported by E. R.
Dowski and W. T. Cathey as mean for increasing depth of field for imaging
systems [1]. Util now, many phase masks of asymmetrical phase mask kind to
increase the depth of field have been reported, such as the cubic phase mask [1],
the logarithmic phase mask [2-5], the sinusoidal phase mask [6, 7], the exponential
phase mask [8], the polynomal phase mask [9], the rational phase mask [10], the
tangent phase mask [11], and the high-order phase mask [12]. All these phase
masks can obtain the aim for large depth extention. Because the modulation
transfer function (MTF) is nearly invariant to defocus and involves no zeros, the
digital processing using a single deconvolution kernel can be used to obtain the
final image near diffation-limited image of a traditional imaging system. However,
as in [13] shown that the restored final images are damaged by the image artifacts,
which come from non-linear phase transfer function (PTF) between the PTF of the
imaging optical transfer function (OTF) and the PTF of the restored OTF. Only
when the restored OTF perfectly matches the imaging OTF, the restored final
image has the best image quality. Recently, a technique to remove image artifacts
was introduced to obtain the restored final image with artifacts-free based on
minimizing of the high frequency content of the restored image [14]. However, this
way need more computation times. Nearly, some methods by using some phase
masks have been introduced to remove image artifacts [15, 16]. However, these
methods are complex and expersive. To decrease ring artifacts, some iterative
restoration techniques have been introduced [17]. The main problem of the
iterative restoration techniques is their computational speed. Recently, another fast
non-iterative technique, which employs Fourier transform based deconvolution
followed by wavelet de-noising, has been presented [18]. Iterative restoration
techniques for ringing artifacts decrease have been introduced for WFC imaging
system with phase masks [19].

Trang 1

Trang 2

Trang 3
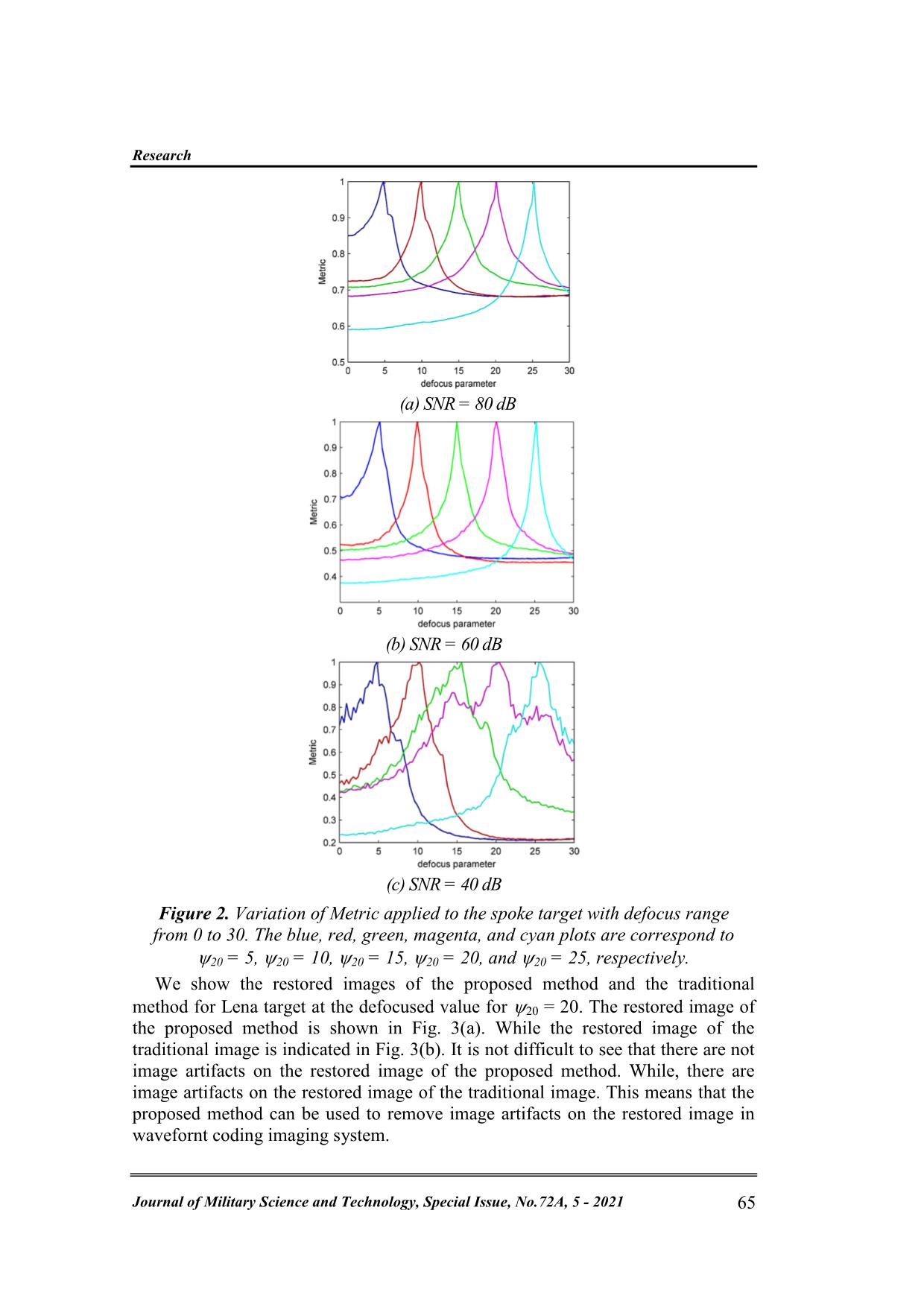
Trang 4
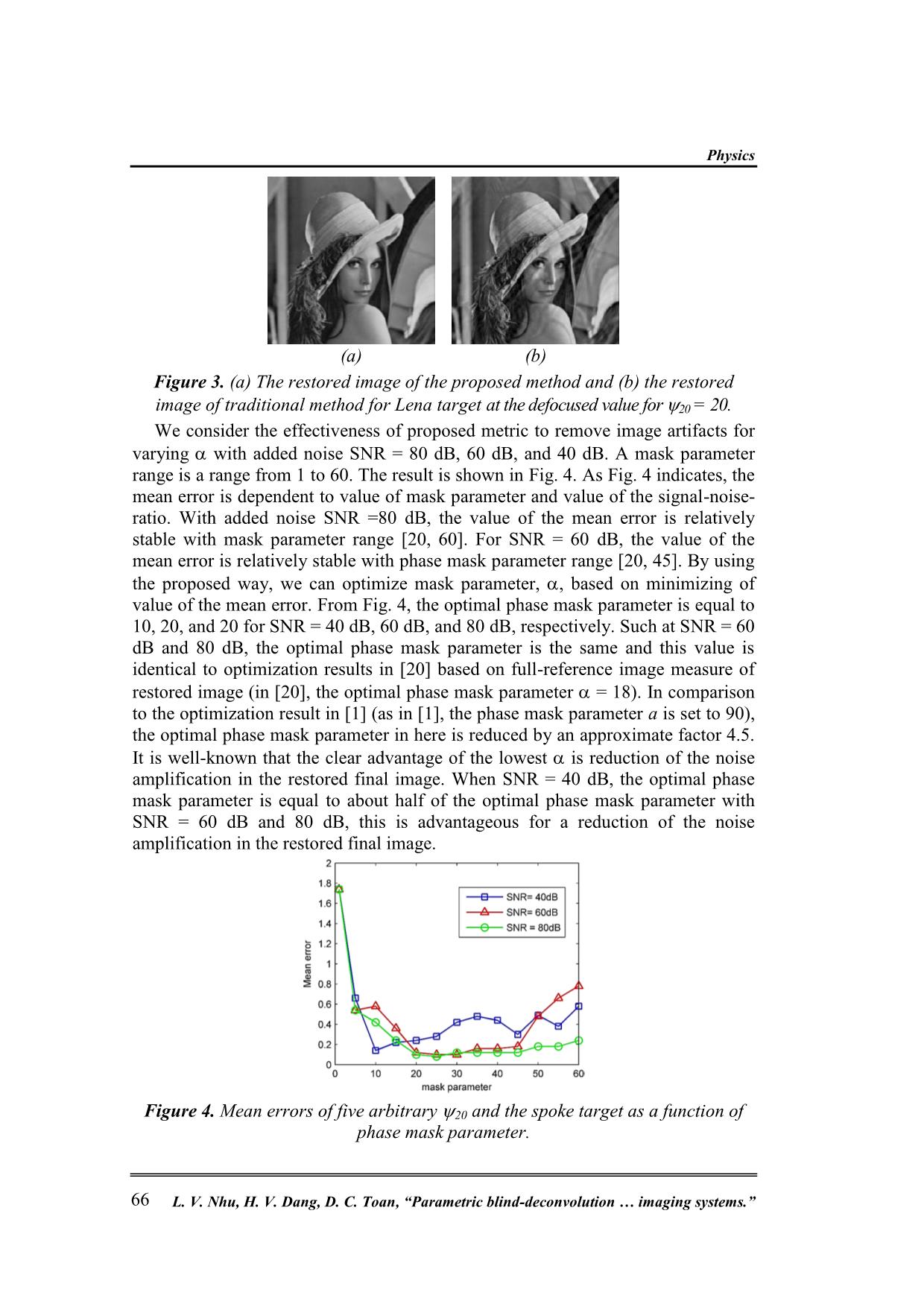
Trang 5
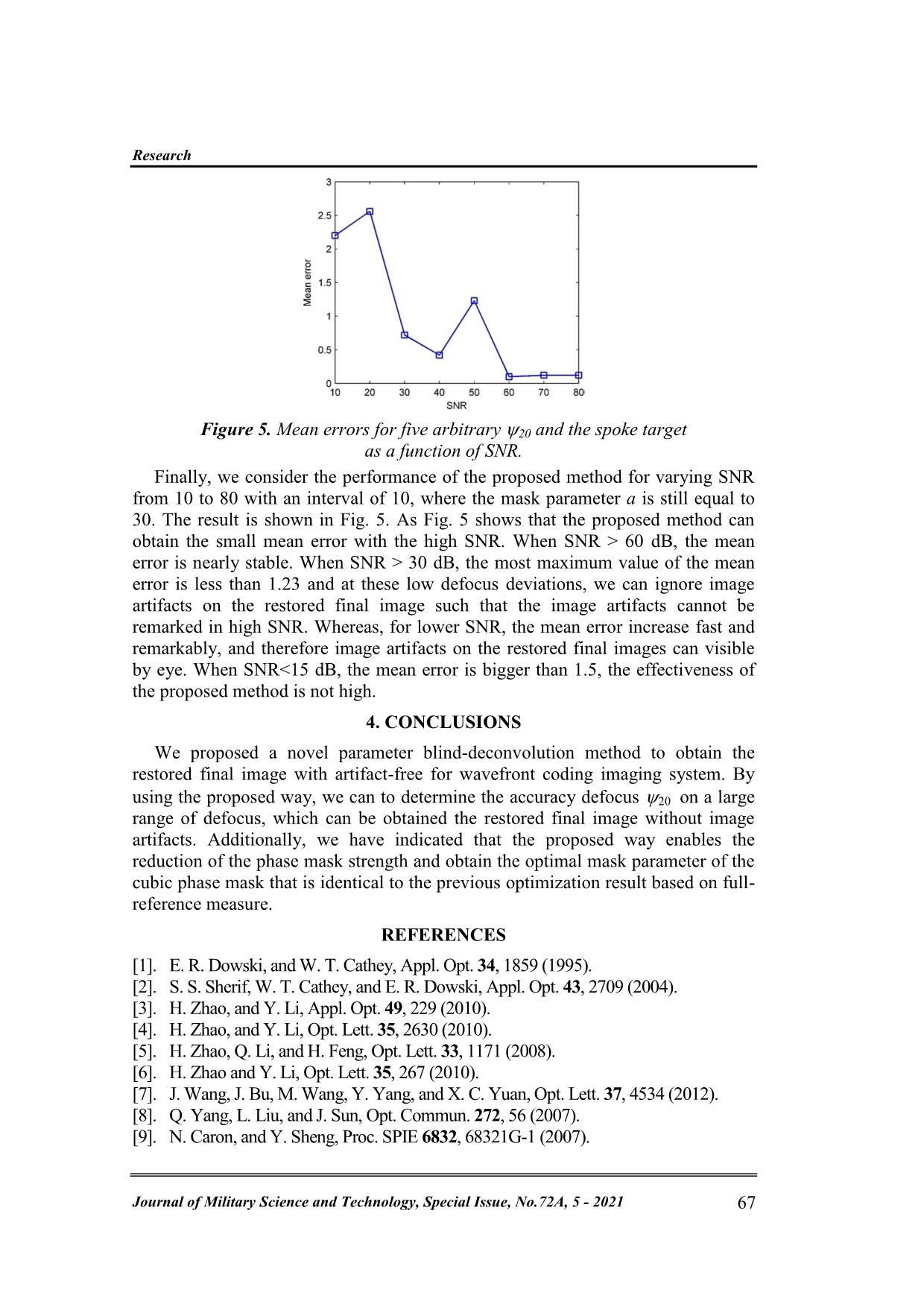
Trang 6

Trang 7
Tóm tắt nội dung tài liệu: Parametric blind - deconvolution method to remove image artifacts in wavefront coding imaging systems

includes a phase mask of asymmetric phase mask kind in the pupil plane to extend the depth of field of an imaging system and the digital processing step to obtain the restored final high-quality image. However, the main drawback of wavefront coding technique is image artifacts on the restored final images. In this paper, we proposed a parameter blind- deconvolution method based on maximizing of the variance of the histogram of restored final images that enables to obtain the restored final image with artifact- free over a large range of defocus. Keywords: Imaging systems; Computational imaging; Deconvolution. 1. INTRODUCTION Since 1995, an asymmetrical cubic phase mask was firstly reported by E. R. Dowski and W. T. Cathey as mean for increasing depth of field for imaging systems [1]. Util now, many phase masks of asymmetrical phase mask kind to increase the depth of field have been reported, such as the cubic phase mask [1], the logarithmic phase mask [2-5], the sinusoidal phase mask [6, 7], the exponential phase mask [8], the polynomal phase mask [9], the rational phase mask [10], the tangent phase mask [11], and the high-order phase mask [12]. All these phase masks can obtain the aim for large depth extention. Because the modulation transfer function (MTF) is nearly invariant to defocus and involves no zeros, the digital processing using a single deconvolution kernel can be used to obtain the final image near diffation-limited image of a traditional imaging system. However, as in [13] shown that the restored final images are damaged by the image artifacts, which come from non-linear phase transfer function (PTF) between the PTF of the imaging optical transfer function (OTF) and the PTF of the restored OTF. Only when the restored OTF perfectly matches the imaging OTF, the restored final image has the best image quality. Recently, a technique to remove image artifacts was introduced to obtain the restored final image with artifacts-free based on minimizing of the high frequency content of the restored image [14]. However, this way need more computation times. Nearly, some methods by using some phase masks have been introduced to remove image artifacts [15, 16]. However, these methods are complex and expersive. To decrease ring artifacts, some iterative restoration techniques have been introduced [17]. The main problem of the iterative restoration techniques is their computational speed. Recently, another fast non-iterative technique, which employs Fourier transform based deconvolution followed by wavelet de-noising, has been presented [18]. Iterative restoration techniques for ringing artifacts decrease have been introduced for WFC imaging system with phase masks [19]. In this paper, we proposed simple image artifacts metric to obtain the restored final image with artifacts-free. The image artifacs metric is based on maximizing 62 L. V. Nhu, H. V. Dang, D. C. Toan, “Parametric blind-deconvolution imaging systems.” Research of variance of the histogram of restored final image, which is known as parameter blind-deconvolution. The image artifact metric enables to determine the restored deconvolution kernel in order to obtain the restored final image with artifacts-free. 2. METHOD We consider the performance of the proposed metric with the most common cubic phase mask. Acoording to Ref. [1], the cubic phase mask can be presented by: f x, y ax33 ay (1) Where: a is the phase mask parameter to control the magnitude of phase deviation; x and y are the coordinates in the pupil plane. A defocused or middle image with added noise for wavefront coding imaging system in the Fourier domain, IMilddle(u, v; 20), where u and v are the spatial frequencies, can be presented by: IMiddle uv, ;,2020 ; ,, Huv OuvNuv (2) Where: H(u, v; 20) is the OTF of wavefront coding imaging system at a given defocus parameter 20; O(u, v) and N(u, v) refer the Fourier transfer of a given scene and noise, respectively. The defocus parameter 20 can be presented by: L2 1 1 1 20 (3) 4 f d0 di r The restored final image in the spatial domain, IFinal(x0, y0; 20 ), with a restored deconvolution kernel, F(u, v; r ), can be described as: 20 I xy,;,;,;rr iFFTI 1 xy Fxy (4) Final 0020 Middle 0020 0020 -1 Where: x0 and y0 are the coordinates in image plane; iFFT is the inverse Fourier transfer. The deconvolution kernel is a Wiener filter given by Eq. (5) as: H* u,; v r r 20 F u,; v 20 2 (5) * r H u,; v 20 K Where: * is the complex conjugate; K is a regularization parameter which optimally is the inverse of the signal-noise-ratio [14]. When the restored deconvolution kernel, F(u, v; r ), is not driven from the 20 imaging OTF, H(u, v; 20), there are image artifacts on the restored final image, while the restored deconvolution kernel, F(u, v; r ), perfectly matches the imaging 20 OTF, H(u, v; 20), the restored final image has no image artifacts. Therefore, the aim r of optimization is to find the value of the optimal filter defocus 20 that is equal to 20, yielding artifacts-free image. In order to resolve this problem, we proposed an r evaluated metric to obtain the optimal value of defocus 20 . The optimal value of Journal of Military Science and Technology, Special Issue, No.72A, 5 - 2021 63 Physics r defocus 20 is determined based on maximizing of a parameter proportional to the variance, VAR, of the histogram of the restored final images. The proposed metric, as a function of defocus parameter, can be presented by: hh min rr Metric VAR 20 20 (6) maxhhrr min 20 20 r Where: h r is the histogram of the restored image, IFinal(x0, y0; 20 ). 20 3. SIMULATION RESULTS In order to evaluate the performance of the proposed metric, first, we describe numerical simulations with a spoke target shown in Fig. 1 and the cubic phase mask with mask parameter of a = 30. 20 is computed for numerical simulations of the five arbitrary, 20 = 5, 20 = 10, 20 = 15, 20 = 20, and 20 = 25 with a defocus parameter range from 0 to 30 in 101 steps. For each restored final image, we add an amount of white Gausses noise for SNR= 80 dB, 60 dB, and 40 dB in the middle image. By using Eq. (6), the result is shown in Fig. 2, where there is a convention that the maximum value of Metric is equal to 1. Fig. 2 (a) shows the result with added noise for SNR = 80 dB. Fig. 2(b) shows the result with added noise for SNR = 60 dB. Fig. 2(c) shows the result with added noise for SNR = 40 r dB. The estimation of the optimal defocus of value 20 is corresponding to the maximum value of these curves. As Fig. 1 shows, it can be seen in all cases that r 20 is approximate to the imaging defocus 20. In the case with added noise for SNR = 80 dB, the mean error for five curves is set to 0.12. In the case with added noise for SNR = 60 dB, the mean error for 5 five curves is equal to 0.10. In the case with added noise for SNR = 40 dB, the mean error for five curves is set to 0.42. With two case SNR = 80 dB and 60 dB, theses curves are smooth, while SNR = 40 dB, these curves have oscillations and the value of the mean error is bigger. Figure 1. Spoke target. 64 L. V. Nhu, H. V. Dang, D. C. Toan, “Parametric blind-deconvolution imaging systems.” Research (a) SNR = 80 dB (b) SNR = 60 dB (c) SNR = 40 dB Figure 2. Variation of Metric applied to the spoke target with defocus range from 0 to 30. The blue, red, green, magenta, and cyan plots are correspond to 20 = 5, 20 = 10, 20 = 15, 20 = 20, and 20 = 25, respectively. We show the restored images of the proposed method and the traditional method for Lena target at the defocused value for 20 = 20. The restored image of the proposed method is shown in Fig. 3(a). While the restored image of the traditional image is indicated in Fig. 3(b). It is not difficult to see that there are not image artifacts on the restored image of the proposed method. While, there are image artifacts on the restored image of the traditional image. This means that the proposed method can be used to remove image artifacts on the restored image in wavefornt coding imaging system. Journal of Military Science and Technology, Special Issue, No.72A, 5 - 2021 65 Physics (a) (b) Figure 3. (a) The restored image of the proposed method and (b) the restored image of traditional method for Lena target at the defocused value for 20 = 20. We consider the effectiveness of proposed metric to remove image artifacts for varying with added noise SNR = 80 dB, 60 dB, and 40 dB. A mask parameter range is a range from 1 to 60. The result is shown in Fig. 4. As Fig. 4 indicates, the mean error is dependent to value of mask parameter and value of the signal-noise- ratio. With added noise SNR =80 dB, the value of the mean error is relatively stable with mask parameter range [20, 60]. For SNR = 60 dB, the value of the mean error is relatively stable with phase mask parameter range [20, 45]. By using the proposed way, we can optimize mask parameter, , based on minimizing of value of the mean error. From Fig. 4, the optimal phase mask parameter is equal to 10, 20, and 20 for SNR = 40 dB, 60 dB, and 80 dB, respectively. Such at SNR = 60 dB and 80 dB, the optimal phase mask parameter is the same and this value is identical to optimization results in [20] based on full-reference image measure of restored image (in [20], the optimal phase mask parameter = 18). In comparison to the optimization result in [1] (as in [1], the phase mask parameter a is set to 90), the optimal phase mask parameter in here is reduced by an approximate factor 4.5. It is well-known that the clear advantage of the lowest is reduction of the noise amplification in the restored final image. When SNR = 40 dB, the optimal phase mask parameter is equal to about half of the optimal phase mask parameter with SNR = 60 dB and 80 dB, this is advantageous for a reduction of the noise amplification in the restored final image. Figure 4. Mean errors of five arbitrary 20 and the spoke target as a function of phase mask parameter. 66 L. V. Nhu, H. V. Dang, D. C. Toan, “Parametric blind-deconvolution imaging systems.” Research Figure 5. Mean errors for five arbitrary 20 and the spoke target as a function of SNR. Finally, we consider the performance of the proposed method for varying SNR from 10 to 80 with an interval of 10, where the mask parameter a is still equal to 30. The result is shown in Fig. 5. As Fig. 5 shows that the proposed method can obtain the small mean error with the high SNR. When SNR > 60 dB, the mean error is nearly stable. When SNR > 30 dB, the most maximum value of the mean error is less than 1.23 and at these low defocus deviations, we can ignore image artifacts on the restored final image such that the image artifacts cannot be remarked in high SNR. Whereas, for lower SNR, the mean error increase fast and remarkably, and therefore image artifacts on the restored final images can visible by eye. When SNR<15 dB, the mean error is bigger than 1.5, the effectiveness of the proposed method is not high. 4. CONCLUSIONS We proposed a novel parameter blind-deconvolution method to obtain the restored final image with artifact-free for wavefront coding imaging system. By using the proposed way, we can to determine the accuracy defocus 20 on a large range of defocus, which can be obtained the restored final image without image artifacts. Additionally, we have indicated that the proposed way enables the reduction of the phase mask strength and obtain the optimal mask parameter of the cubic phase mask that is identical to the previous optimization result based on full- reference measure. REFERENCES [1]. E. R. Dowski, and W. T. Cathey, Appl. Opt. 34, 1859 (1995). [2]. S. S. Sherif, W. T. Cathey, and E. R. Dowski, Appl. Opt. 43, 2709 (2004). [3]. H. Zhao, and Y. Li, Appl. Opt. 49, 229 (2010). [4]. H. Zhao, and Y. Li, Opt. Lett. 35, 2630 (2010). [5]. H. Zhao, Q. Li, and H. Feng, Opt. Lett. 33, 1171 (2008). [6]. H. Zhao and Y. Li, Opt. Lett. 35, 267 (2010). [7]. J. Wang, J. Bu, M. Wang, Y. Yang, and X. C. Yuan, Opt. Lett. 37, 4534 (2012). [8]. Q. Yang, L. Liu, and J. Sun, Opt. Commun. 272, 56 (2007). [9]. N. Caron, and Y. Sheng, Proc. SPIE 6832, 68321G-1 (2007). Journal of Military Science and Technology, Special Issue, No.72A, 5 - 2021 67 Physics [10]. F. Zhou, G. Li, H. Zhang, and D. Wang, Opt. Lett. 34, 380 (2009). [11]. V. N. Le, Z. Fan, and S. Chen, Opt. Lett. 39, 2171 (2014). [12]. A. Sauceda, and J. Ojeda-Castañeda, Opt. Lett. 29, 560 (2004). [13]. M. Demenikov, and A. R. Harvey, Opt. Express. 18, 18035 (2010). [14]. M. Demenikov, and A. R. Harvey, Opt. Express. 18, 8207 (2010). [15]. H. Du, Rigui Yi, L. Dong, M. Liu, W. ia, Y. Zhao, X. Liu, M. Hui, L. Kong, and X. Chen, Applied Optics, 57, 3365, (2018). [16]. P. Zammit, A. R. Harvey, G. Carles, Optica, 1 (4), 209-216 (2010). [17]. R. L. Lagendijk, J. Biemond, D. E. Boekee, IEEE Transactions on Acoustics, “Speech and Signal Processing”, Vol. 36, Issue 12, 1874-1888 (1988). [18]. R. Neelamani, H. Choi, R. Baraniuk, IEEE Transaction on Signal Processing, Vol. 52, 418-433 (2004). [19]. J. V. D. Gracht, J. G. Nagy, V. Pauca V, et al, “In Integrated Computational imaging systems”, Optical Society of America, (2001). [20]. T. Vettenburg, N. Bustin, and A. R. Harvey, Opt. Express. 18, 9220 (2010). TÓM TẮT PHƯƠNG PHÁP CUỘC ĐẢO NGƯỢC MỜ CHO LOẠI BỎ TẠP CHẤT Ở HỆ THỐNG MÃ HÓA MẶT SÓNG Công nghệ mã hóa mặt sóng bao gồm đồng thời phần quang học và xử lý ảnh. Phần quang học là một mặt nạ pha đặt tại mặt phẳng đồng tử ra của hệ thống quang học truyền thống đưa đến ảnh mờ đồng đều trên một độ sâu trường lớn. Phần xử lý ảnh truyền thống được thực hiện bằng sử dụng một phin lọc nghịch đảo để nhận ảnh sắc nét trên độ sâu trường lớn. Tuy nhiên, nhược điểm chính của kỹ thuật xử lý ảnh này là làm xuất hiện tạp chất trên ảnh khôi phục. Trong bài báo này, chúng tôi đề xuất phương pháp cuộn nghịch đảo mờ trên cơ sở tối ưu hóa hàm histogram của tập ảnh khôi phục với các độ sâu trường để nhận được ảnh khôi phục chất lượng cao mà không bị xuất hiện tạp chất trên ảnh. Từ khóa: Các hệ thống tạo ảnh; Tạo ảnh tính toán; Cuộc nghịch đảo. Received 2nd March 2021 Revised 27th April 2021 Accepted 10th May 2021 Author affiliations: 1Học viện Kỹ thuật quân sự; 2Viện Vũ khí, Tổng cục Công nghiệp Quốc phòng. *Corresponding author: levannhuktq@gmail.com. 68 L. V. Nhu, H. V. Dang, D. C. Toan, “Parametric blind-deconvolution imaging systems.”
File đính kèm:
 parametric_blind_deconvolution_method_to_remove_image_artifa.pdf
parametric_blind_deconvolution_method_to_remove_image_artifa.pdf

