Nhận dạng ổn định hệ thống điện dùng bộ phân lớp SVM

 giải quyết những vấn đề khó 
khăn mà những phương pháp phân tích 
truyền thống không giải quyết được về tốc độ 
tính toán [1]. Bằng quá trình học cơ sở dữ 
liệu vào ra giữa những thông số vận hành 
HTĐ, trạng thái ổn định HTĐ có thể tính 
toán một cách nhanh chóng [2], [3]. Ma trận 
2 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 57 (04/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
cơ sở dữ liệu ổn định HTĐ bao gồm biến và 
mẫu như Hình 1, trong đó x là biến đầu vào 
gồm n biến, N mẫu. Biến đầu ra y có N mẫu 
gán nhãn nhị phân. 
11 12 1
21 22 2
1 2
...
...
... ... ... ...
...
n
n
N N NN
x x x
x x x
x x x
Hình 1. Ma trận cơ sở dữ liệu 
Bài toán đánh giá ổn định HTĐ là bài 
toán phi tuyến phức tạp. Nhiều công trình 
công bố áp dụng mạng nơ-rôn để thiết kế bộ 
phân lớp đánh giá ổn định HTĐ [2]–[4].Tuy 
nhiên, áp dụng mạng nơ-rôn gặp phải vấn đề 
khó khăn trong huấn luyện là dễ bị rơi vào 
cực trị địa phương. Để giải bài toán phân lớp 
phi tuyến cao, bộ phân lớp SVM là lựa chọn 
hứa hẹn cho đánh giá ổn định HTĐ. Bài báo 
đề nghị áp dụng bộ phân lớp SVM vào đánh 
giá ổn định HTĐ. Bài báo đã so sánh độ 
chính xác nhận dạng ổn định HTĐ của SVM 
và mạng nơ-rôn MLP. Kết quả cho thấy bộ 
phân lớp SVM đạt độ chính xác nhận dạng 
cao hơn bộ phân lớp MLP. 
2. LỰA CHỌN BIẾN ĐẶC TRƯNG 
Trong các giai đoạn thiết kế mô hình 
đánh giá ổn định HTĐ dùng phương pháp 
nhận dạng, lựa chọn biến hay giảm biến có 
lợi ích trong việc giảm không gian dữ liệu, 
giúp giảm dung lượng lưu trữ bộ nhớ. Quy 
trình lựa chọn biến được giới thiệu trong [5], 
[6], và được trình bày ở Hình 2. 
yes
Lựa chọn biến đặc 
trưng ban đầu
Tìm kiếm biến đặc 
trưng ứng viên
Đánh giá biến đặc 
trưng ứng viên
Output
Tiêu chuẩn dừng
no
Start
Hình 2. Quy trình lựa chọn biến 
3. Bộ phân lớp MLP và SVM 
3.1. MLP 
Cấu trúc MLP cơ bản như Hình 3 gồm có 
lớp ngõ vào, một hay nhiều lớp ẩn và lớp ngõ 
ra. 
x1
x2
xn
Input 
Hidden 
layer
Output
 layer
Output
Input 
layer
Hình 3. Mạng MLP 
Số lớp ẩn có thể thay đổi trong quá trình 
huấn luyện tùy thuộc dữ liệu bài toán. Các 
nút ngõ ra có giá trị thay đổi phụ thuộc vào 
lớp ngõ ra mục tiêu. Huấn luyện phổ biến là 
học có giám sát với giải thuật lan truyền 
ngược. Có nhiều giải thuật huấn luyện, trong 
đó thuật toán Levenberg-Marquardt có hiệu 
suất cao hơn và tốc độ hội tụ nhanh hơn [7]. 
Thông số mạng ban đầu là ngẫu nhiên, quá 
trình huấn luyện dừng khi số vòng lặp đạt giá 
trị tối đa cài đặt, sai số đạt một mức cho phép 
hoặc sai số không tăng nữa. 
3.2. SVM 
Thuật toán bộ nhận dạng SVM là thực 
hiện phân lớp các mẫu dựa trên phương pháp 
tiếp cận lý thuyết học thống kê do Vanipk và 
Chervonenkis đề nghị [8]. SVM nhằm cực 
tiểu hóa độ phân lớp sai với một đối tượng 
dữ liệu mới thông qua cực đại hóa biên giữa 
siêu phẳng phân cách và dữ liệu. Ý tưởng cơ 
bản của các SVM là xây dựng một siêu 
phẳng như là một mặt phẳng quyết định. Mặt 
phẳng này tách biệt lớp dương (+1) và lớp 
âm (-1) với biên lớn nhất. Xét tập dữ liệu 
huấn luyện 1{x , y }
N
i i iT , trong đó, xi là vectơ 
dữ liệu đầu vào kích thước n biến và N mẫu, 
và yi {+1,-1} là nhãn lớp của mẫu xi. Các 
SVM thực thi cho bài toán phân lớp có hai 
lớp được minh họa như Hình 4. Siêu phẳng 
tối ưu phân tách các mẫu dương và các mẫu 
âm của hai lớp với độ tách biệt cực đại. Độ 
tách biệt hay là biên xác định bằng khoảng 
cách giữa các mẫu dương và mẫu âm gần mặt 
siêu phẳng nhất. 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 57 (04/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
3 
Các vec-tơ hỗ trợ
x1
x2
Lớp yi=-1
Lớp yi=+1
Mặt siêu phẳng tối ưu
Biên tối ưu
Hình 4. Sơ đồ thuật toán SVM 
Mặt siêu phẳng trong không gian mẫu có 
phương trình (1): 
g(x)= wT.x+b=0 (1) 
Mục đích của huấn luyện là tìm ra một 
siêu phẳng tách biệt dữ liệu huấn luyện tốt 
nhất. Mặt siêu phẳng tách rời các mẫu âm và 
dương thỏa điều kiện (2) và (3). 
 wT.xi+ b 0, nếu yi=+1 (2) 
 wT.xi+ b 0, nếu yi= -1 (3) 
Siêu phẳng tối ưu như phương trình (1) là 
siêu phẳng duy nhất tách tập dữ liệu học với 
biên cực đại. Nó xác định hướng w/|w| mà 
khoảng cách từ hình chiếu các vector học của 
2 lớp là lớn nhất. Khoảng cách từ một điểm 
đến siêu phẳng được tính theo phương trình 
(4), với biên là 
2
w
. 
( )g x
z
w
 (4) 
Với mỗi điểm xi tương ứng thuộc nhãn 
lớp yi, cần xác định tập thông số (w, b) của 
siêu phẳng theo (5). 
21
Min (w)
2
(w x b) 1
w
T
i i
w
y
 
(5) 
Trong trường hợp dữ liệu bài toán phức 
tạp và bị chồng lấn, nhiễu, khó tách biệt thì bài 
toán (5) trở thành bài toán (6). 
2
1
1
Min (w, )
2
(w (x ) b) 1
0
N
i
w
i
T
i i i
i
w C
y
 


 
 

(6) 
Trong đó, w là trọng số của mặt siêu 
phẳng. C là hệ số phạt định nghĩa giá trị ràng 
buộc. (.) là hàm ánh xạ, b là hệ số ngưỡng, 
i là biến nới lỏng, i 0. 
3.3. Đánh giá mô hình nhận dạng 
Phần trăm độ chính xác nhận dạng của 
mô hình được tính theo phương trình (7). 
R
CR% .100
D
(7) 
Trong đó: R là số mẫu đúng trong tập 
mẫu, D là tổng số mẫu của tập mẫu. 
4. ÁP DỤNG NHẬN DẠNG ỔN ĐỊNH 
ĐỘNG HTĐ IEEE 10 MÁY 39-BUS 
4.1. Sơ đồ IEEE 10 máy 39-bus 
HTĐ IEEE 39-bus gồm có 39 bus, trong đó 
10 bus máy phát, 12 máy biến áp, 10 máy 
phát, 34 đường dây truyền tải và 19 tải. 10 
máy phát được kết nối từ bus 30 đến bus 39, 
trong đó bus 39 được coi là bus Slack, 9 bus 
được gọi là bus PV, 29 bus còn lại được gọi 
là bus PQ, có 2 cấp điện áp là 345kV và 
20kV. Hệ thống được cho như ở Hình 5. 
Hình 5. HTĐ IEEE 39-bus 
4.2. Tạo cơ sở dữ liệu 
Có hai dạng biến cho chế độ hệ thống 
điện là biến chứa dữ liệu ở chế độ xác lập và 
ở chế độ sự cố. Biến ở chế độ xác lập hay 
tiền sự cố là thông tin giúp hệ thống nhận 
dạng biết tình trạng mất ổn định xảy ra để 
phát tín hiệu đến hệ thống điều khiển ngăn 
chặn trước, giúp hệ thống điều khiển ra quyết 
định đưa hệ thống điện vào vùng vận hành an 
toàn, phòng khi sự cố xảy ra gây mất ổn định 
4 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 57 (04/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
hệ thống điện, mặc dù thực tế là sự cố có thể 
không xảy ra. Hẳn nhiên, việc điều khiển này 
phải chịu chi phí tổn thất cho việc điều chỉnh 
lại lịch trình phát của các máy phát điện. Đặc 
trưng cho chế độ tiền sự cố là các điểm vận 
hành hệ thống điện gồm điện áp tại các bus, 
công suất các máy phát điện, dòng công suất 
trên các nhánh, công suất của các tải,Biến 
ở chế độ động hay chế độ sự cố là thông tin 
cho biết tình trạng mất ổn định xảy ra để phát 
tín hiệu đến hệ thống điều khiển khẩn cấp và 
lệnh điều khiển ngay lập tức phải được thi 
hành để đưa hệ thống trở về trạng thái ổn 
định, cứu hệ thống điện khỏi nguy cơ tan rã. 
Đặc trưng chế độ sự cố gồm độ lệch điện áp 
tại các bus, độ lệch công suất phát, độ lệch 
công suất trên các nhánh, độ lệch công suất 
các tải, Trong thực tế phân tích ổn định hệ 
thống điện thì độ sụt điện áp và độ thay đổi 
công suất tác dụng chứa thông tin rất cao và 
liên quan trực tiếp đến trạng thái ổn định hệ 
thống điện. Đây là các biến có chứa thông tin 
cao được lựa chọn làm biến đầu vào cho bộ 
nhận dạng. Biến đầu ra đại diện cho điều 
kiện ổn định động của hệ thống điện được 
gán nhãn biến nhị phân cho lớp ổn định và 
lớp không ổn định. 
Phần mềm Powerworld tính toán mẫu 
công suất phát tương ứng nhờ công cụ tính 
toán phân bố công suất tối ưu OPF. Thực 
hiện mô phỏng off-line để thu thập dữ liệu 
cho đánh giá ổn định động HTĐ, trong 
nghiên cứu này xét hệ thống điện ở chế độ 
vận hành đầy đủ các máy phát và các đường 
dây truyền tải, mức tải 100% tải cơ bản, thời 
gian cắt ngắn mạch cài đặt là 50ms. Bài báo 
này xem xét các sự cố ngắn mạch ba pha, 
một pha chạm đất, hai pha tại tất cả các thanh 
góp và dọc các đường dây truyền tải với mỗi 
khoảng cách 5% chiều dài đường dây. Biến 
đầu vào là: x{∆Vbus, ∆Pload, ∆Pflow}. Tổng số 
biến đầu vào là 104(39+19+46), 1 biến đầu 
ra. Tổng số mẫu là 310 mẫu, trong đó có 158 
mẫu ổn định và 152 mẫu không ổn định. 
4.3. Biến đầu vào và biến đầu ra 
Để chọn tập biến, trong bài báo này tác 
giả đề xuất áp dụng phương pháp xếp hạng 
với hàm mục tiêu chọn biến F (Fisher) [5] và 
phương pháp tìm kiếm tuần tự tiến lùi 
(SFFS) với hàm mục tiêu SM 
(Scatter-Matrice) [9]. Đây là hai phương 
pháp đã được áp dụng chọn biến và công bố 
trong bài báo [5], [6]. 
Để tiến hành chọn biến, tập dữ liệu được 
chia ngẫu nhiên làm 10 tập con có kích cỡ 
bằng nhau. Mỗi lần huấn luyện với chín tập 
con và một tập con còn lại làm tập kiểm tra. 
Kết quả huấn luyện và kiểm tra được tính 
toán trung bình cho 10 lần thực hiện. Bài báo 
áp dụng bộ nhận dạng K-Nearest Neighbor 
(1-NN, K=1) để thực hiện đánh giá độ chính 
xác chọn tập biến nhờ vào tính đơn giản của 
nó. Độ chính xác kiểm tra khi chọn biến theo 
phương pháp xếp hạng và SFFS là 93,5% và 
95,8% tương ứng với số biến là 15 và 14 
biến. Kết quả số biến được chọn là 14 biến 
theo phương pháp SFFS. Kết quả chọn biến 
này sẽ được sử dụng để xây dựng mô hình bộ 
nhận dạng hay bộ phân lớp ở phần trình bày 
tiếp sau. 
4.4. Xây dựng mô hình mạng bộ phân lớp 
Phân chia dữ liệu: 
Tập dữ liệu xây dựng mô hình có 310 
mẫu với 14 biến đầu vào, một biến ngõ ra. 
Tập mẫu huấn luyện có 230 mẫu, trong đó 
118 mẫu ổn định và 112 mẫu không ổn định. 
Tập mẫu kiểm tra có 80 mẫu, trong đó có 40 
mẫu ổn định và 40 mẫu không ổn định. 
Trong bài báo này sử dụng các công cụ nhận 
dạng được hỗ trợ của phần mềm Matlab. 
Xây dựng mô hình mạng MLP: 
Hình 6. Đặc tuyến hội tụ huấn luyện mạng 
MLP 
0 10 20 30
10
-4
10
-2
10
0
M
S
E
Epochs
Train
Validation
Test
Best
Goal
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 57 (04/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
5 
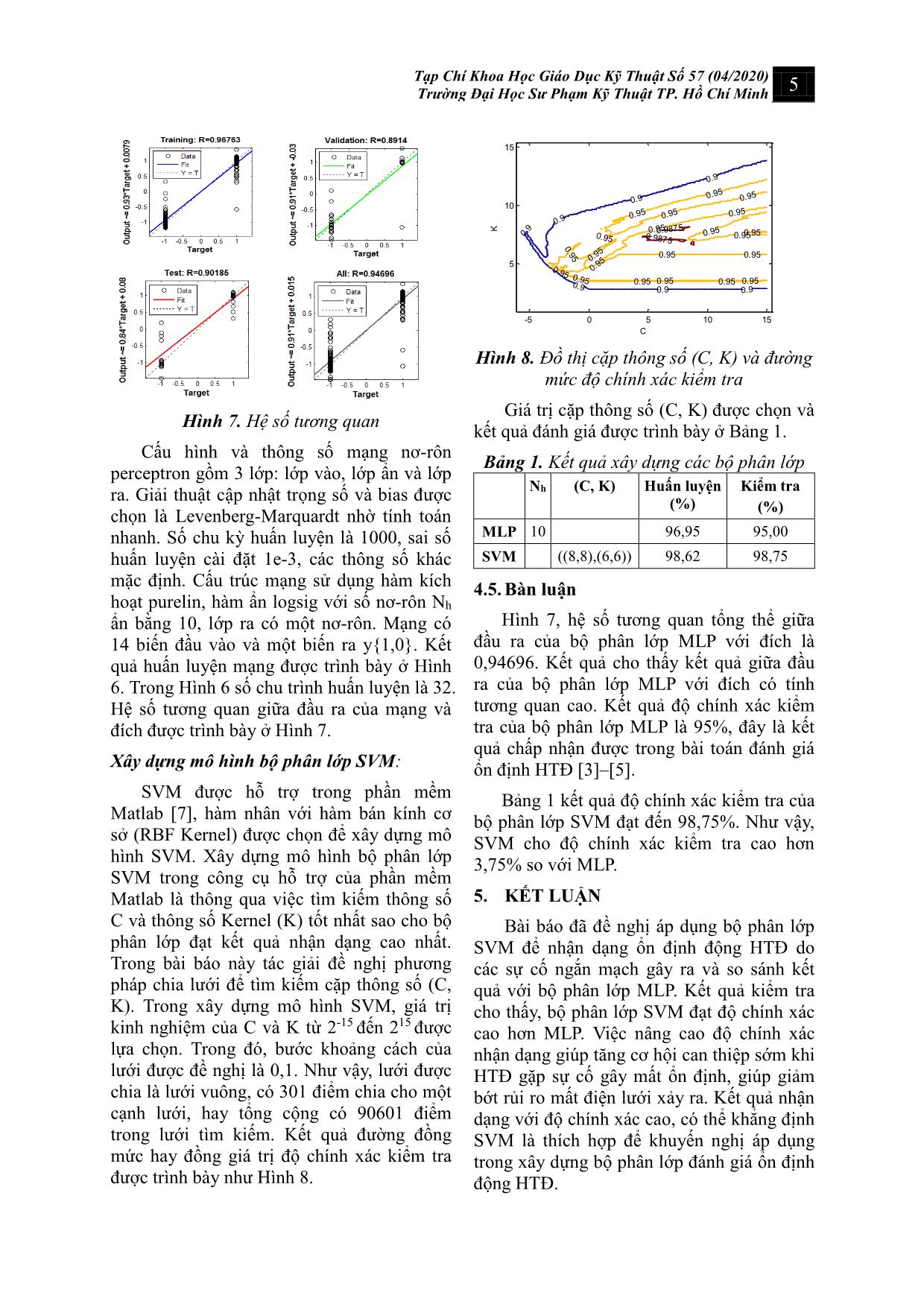
Hình 7. Hệ số tương quan 
Cấu hình và thông số mạng nơ-rôn 
perceptron gồm 3 lớp: lớp vào, lớp ẩn và lớp 
ra. Giải thuật cập nhật trọng số và bias được 
chọn là Levenberg-Marquardt nhờ tính toán 
nhanh. Số chu kỳ huấn luyện là 1000, sai số 
huấn luyện cài đặt 1e-3, các thông số khác 
mặc định. Cấu trúc mạng sử dụng hàm kích 
hoạt purelin, hàm ẩn logsig với số nơ-rôn Nh 
ẩn bằng 10, lớp ra có một nơ-rôn. Mạng có 
14 biến đầu vào và một biến ra y{1,0}. Kết 
quả huấn luyện mạng được trình bày ở Hình 
6. Trong Hình 6 số chu trình huấn luyện là 32. 
Hệ số tương quan giữa đầu ra của mạng và 
đích được trình bày ở Hình 7. 
Xây dựng mô hình bộ phân lớp SVM: 
SVM được hỗ trợ trong phần mềm 
Matlab [7], hàm nhân với hàm bán kính cơ 
sở (RBF Kernel) được chọn để xây dựng mô 
hình SVM. Xây dựng mô hình bộ phân lớp 
SVM trong công cụ hỗ trợ của phần mềm 
Matlab là thông qua việc tìm kiếm thông số 
C và thông số Kernel (K) tốt nhất sao cho bộ 
phân lớp đạt kết quả nhận dạng cao nhất. 
Trong bài báo này tác giải đề nghị phương 
pháp chia lưới để tìm kiếm cặp thông số (C, 
K). Trong xây dựng mô hình SVM, giá trị 
kinh nghiệm của C và K từ 2-15 đến 215 được 
lựa chọn. Trong đó, bước khoảng cách của 
lưới được đề nghị là 0,1. Như vậy, lưới được 
chia là lưới vuông, có 301 điểm chia cho một 
cạnh lưới, hay tổng cộng có 90601 điểm 
trong lưới tìm kiếm. Kết quả đường đồng 
mức hay đồng giá trị độ chính xác kiểm tra 
được trình bày như Hình 8. 
Hình 8. Đồ thị cặp thông số (C, K) và đường 
mức độ chính xác kiểm tra 
Giá trị cặp thông số (C, K) được chọn và 
kết quả đánh giá được trình bày ở Bảng 1. 
Bảng 1. Kết quả xây dựng các bộ phân lớp 
 Nh (C, K) Huấn luyện 
(%) 
Kiểm tra 
(%) 
MLP 10 96,95 95,00 
SVM ((8,8),(6,6)) 98,62 98,75 
4.5. Bàn luận 
 Hình 7, hệ số tương quan tổng thể giữa 
đầu ra của bộ phân lớp MLP với đích là 
0,94696. Kết quả cho thấy kết quả giữa đầu 
ra của bộ phân lớp MLP với đích có tính 
tương quan cao. Kết quả độ chính xác kiểm 
tra của bộ phân lớp MLP là 95%, đây là kết 
quả chấp nhận được trong bài toán đánh giá 
ổn định HTĐ [3]–[5]. 
 Bảng 1 kết quả độ chính xác kiểm tra của 
bộ phân lớp SVM đạt đến 98,75%. Như vậy, 
SVM cho độ chính xác kiểm tra cao hơn 
3,75% so với MLP. 
5. KẾT LUẬN 
Bài báo đã đề nghị áp dụng bộ phân lớp 
SVM để nhận dạng ổn định động HTĐ do 
các sự cố ngắn mạch gây ra và so sánh kết 
quả với bộ phân lớp MLP. Kết quả kiểm tra 
cho thấy, bộ phân lớp SVM đạt độ chính xác 
cao hơn MLP. Việc nâng cao độ chính xác 
nhận dạng giúp tăng cơ hội can thiệp sớm khi 
HTĐ gặp sự cố gây mất ổn định, giúp giảm 
bớt rủi ro mất điện lưới xảy ra. Kết quả nhận 
dạng với độ chính xác cao, có thể khẳng định 
SVM là thích hợp để khuyến nghị áp dụng 
trong xây dựng bộ phân lớp đánh giá ổn định 
động HTĐ. 
0.9
0.9
0.9
0.
9
0.9 0.9 0.9
0.95
0.95
0.95
0.95
0.95
0.95
0.95
0.
95
0.95 0.95
0.95 0.950.95
0.950.95
0.95
0.95 0.
95
0.95 0.95 0.95
0.9875
0.9875
C
K
-5 0 5 10 15
5
10
15
6 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 57 (04/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
TÀI LIỆU THAM KHẢO 
[1] R. Zhang, Y. Xu, Z. Y. Dong, K. Meng, and Z. Xu, “Intelligent systems for power 
system dynamic security assessment: Review and classification,” 2011 4th Int. Conf. 
Electr. Util. Deregul. Restruct. Power Technol., pp. 134–139, 2011. 
[2] S. Kalyani and K. S. Swarup, “Pattern analysis and classification for security evaluation 
in power networks,” Int. J. Electr. Power Energy Syst., vol. 44, no. 1, pp. 547–560, 
2013. 
[3] A. Karami and S. Z. Esmaili, “Transient stability assessment of power systems 
described with detailed models using neural networks,” Int. J. Electr. Power Energy 
Syst., vol. 45, no. 1, pp. 279–292, 2013. 
[4] A. M. A. Haidar, M. W. Mustafa, F. A. F. Ibrahim, and I. A. Ahmed, “Transient stability 
evaluation of electrical power system using generalized regression neural networks,” 
Appl. Soft Comput. J., vol. 11, no. 4, pp. 3558–3570, 2011. 
[5] Z. Y. Dong, Z. Rui, and Y. Xu,“Feature selection for intelligent stability assessment of 
power systems,” IEEE Power and Energy Society General Meeting, pp. 1–7, 2012. 
[6] N.N.Au, Q.H.Anh, and P.T.T.Binh, “Feature Subset Selection in Dynamic Stability 
Assessment Power System Using Artificial Neural Networks,” Sci. Technol. Dev. Vol.18, 
No.K3, 2015. 
[7] M. H. Beale, M. T. Hagan, and H. B. Demuth, “Neural Network Toolbox TM User ’ s 
Guide R 2014 a,” 2014. 
[8] C. Cortes and V. Vapnik, “Support-Vector Networks,” Proc. Mach. Learn., vol. 20, pp. 
273–297, 1995. 
[9] A. R. Webb and K. D. Copsey, ''Statistical Pattern Recognition'', Third Edition, A John 
Wiley & Sons. Inc. Publication, 2011. 
Tác giả chịu trách nhiệm bài viết: 
Nguyễn Ngọc Âu 
Trường Đại học Sư phạm Kỹ thuật TP.HCM 
Email: aunn@hcmute.edu.vn