Nghiên cứu và xây dựng mô hình toán học cho hệ thống thủy điện liên kết vùng trong bài toán ổn định tốc độ tuabin

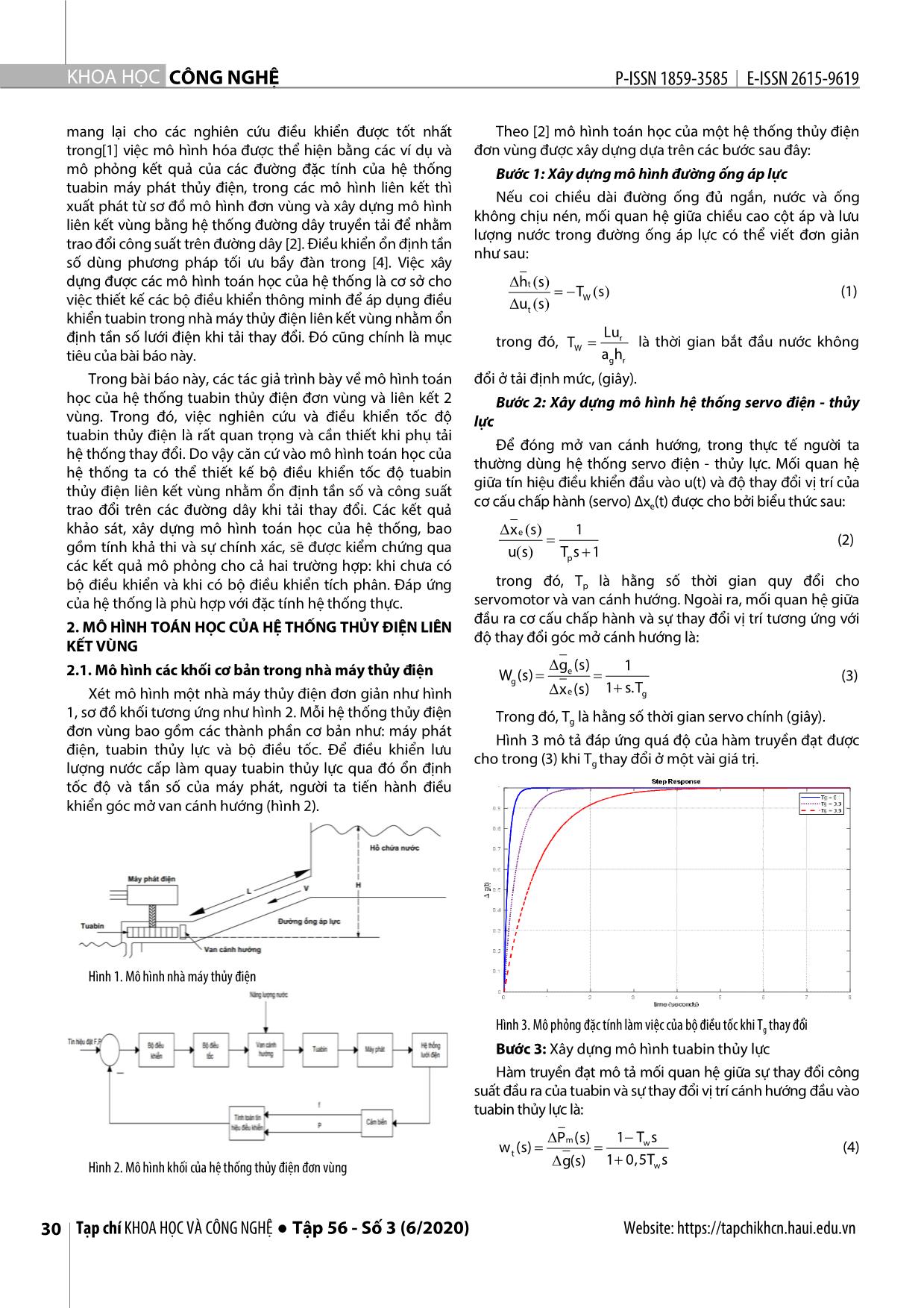
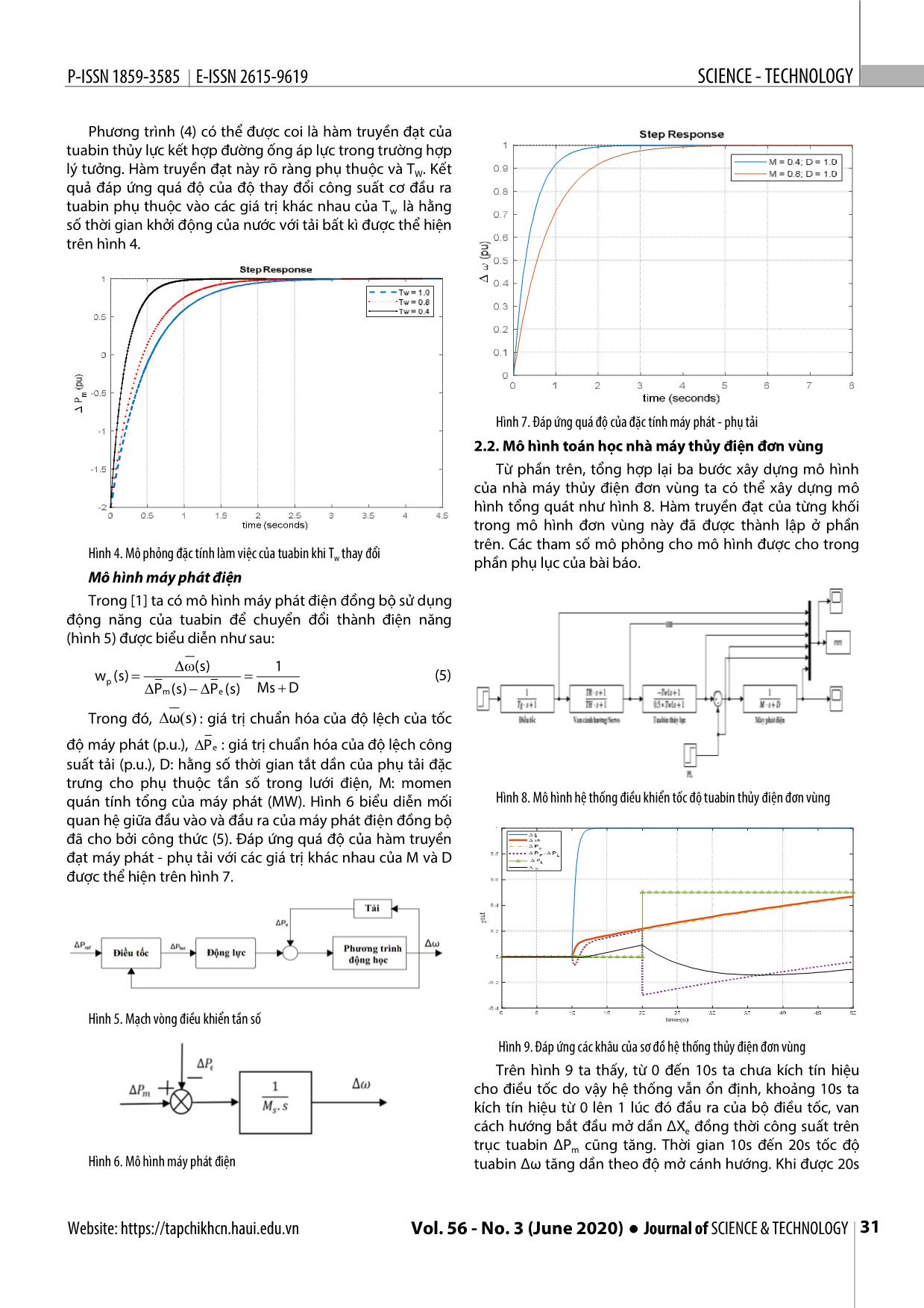
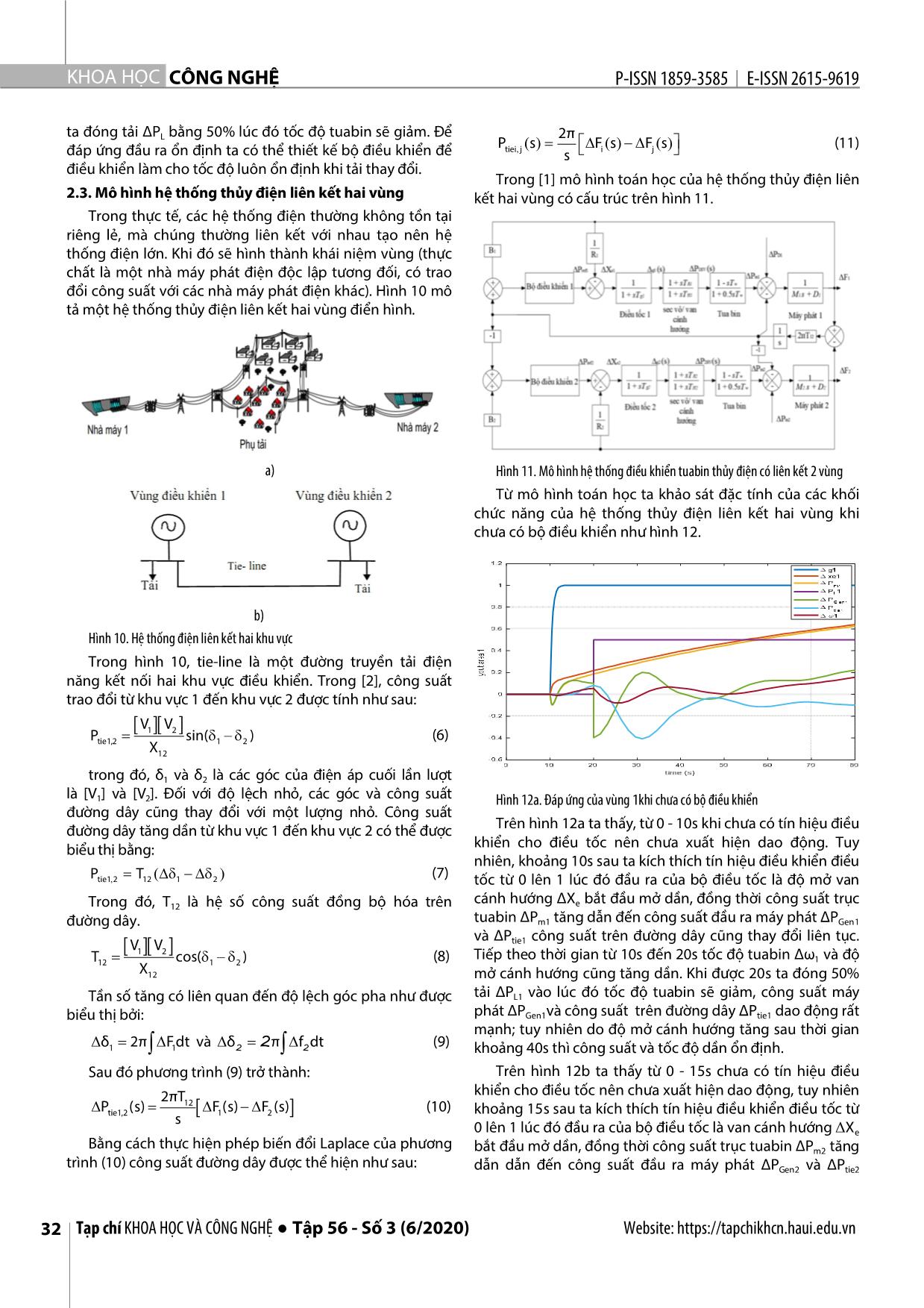
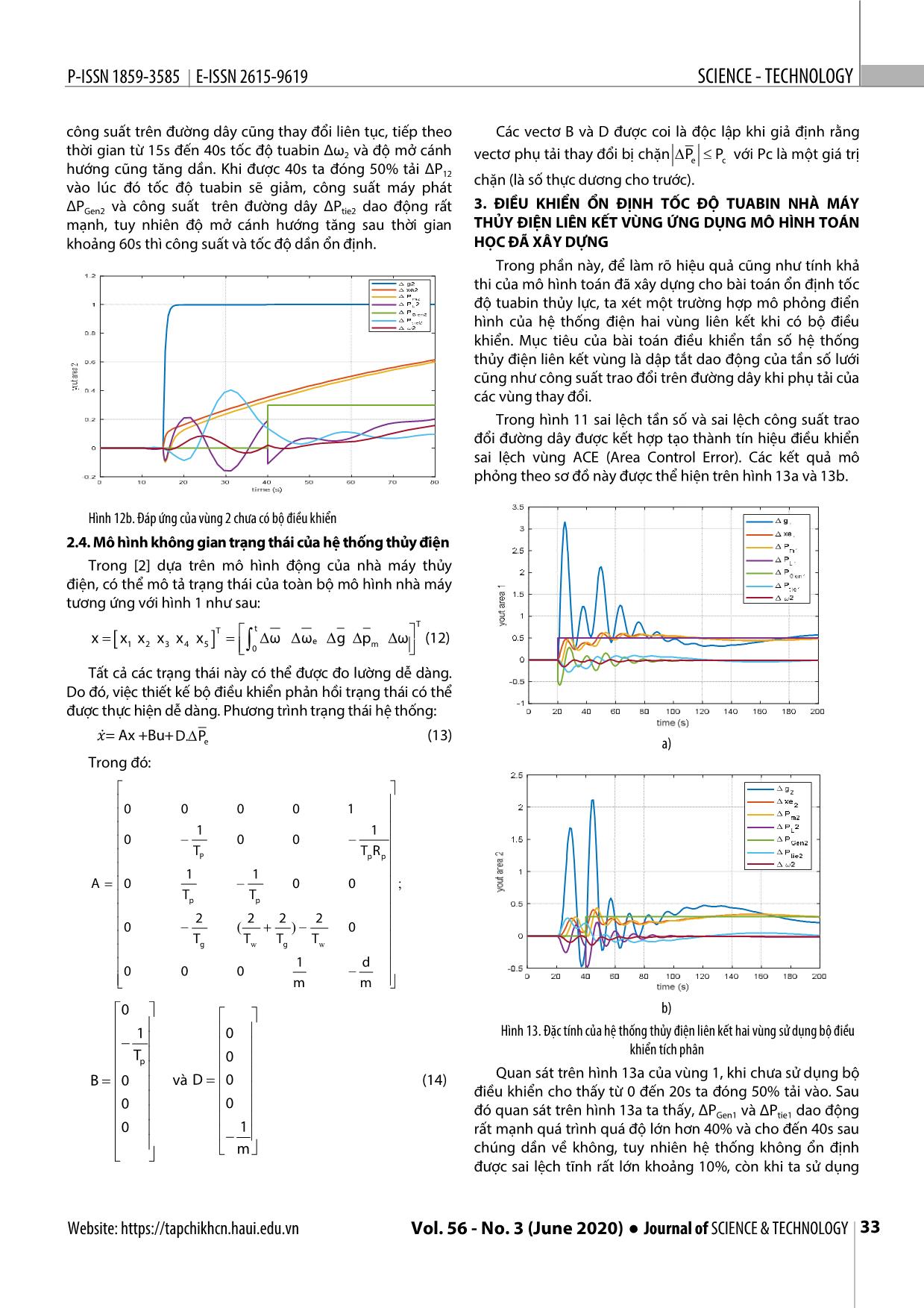
n thủy điện đơn vùng và liên kết 2 Bước 2: Xây dựng mô hình hệ thống servo điện - thủy 
 vùng. Trong đó, việc nghiên cứu và điều khiển tốc độ lực 
 tuabin thủy điện là rất quan trọng và cần thiết khi phụ tải 
 Để đóng mở van cánh hướng, trong thực tế người ta 
 hệ thống thay đổi. Do vậy căn cứ vào mô hình toán học của 
 thường dùng hệ thống servo điện - thủy lực. Mối quan hệ 
 hệ thống ta có thể thiết kế bộ điều khiển tốc độ tuabin 
 giữa tín hiệu điều khiển đầu vào u(t) và độ thay đổi vị trí của 
 thủy điện liên kết vùng nhằm ổn định tần số và công suất 
 cơ cấu chấp hành (servo) ∆x (t) được cho bởi biểu thức sau: 
 trao đổi trên các đường dây khi tải thay đổi. Các kết quả e
 khảo sát, xây dựng mô hình toán học của hệ thống, bao xe () s 1
 gồm tính khả thi và sự chính xác, sẽ được kiểm chứng qua (2) 
 u() s Tp s 1
 các kết quả mô phỏng cho cả hai trường hợp: khi chưa có 
 bộ điều khiển và khi có bộ điều khiển tích phân. Đáp ứng trong đó, Tp là hằng số thời gian quy đổi cho 
 của hệ thống là phù hợp với đặc tính hệ thống thực. servomotor và van cánh hướng. Ngoài ra, mối quan hệ giữa 
 đầu ra cơ cấu chấp hành và sự thay đổi vị trí tương ứng với 
 2. MÔ HÌNH TOÁN HỌC CỦA HỆ THỐNG THỦY ĐIỆN LIÊN 
 độ thay đổi góc mở cánh hướng là: 
 KẾT VÙNG 
 g (s) 1
 2.1. Mô hình các khối cơ bản trong nhà máy thủy điện W (s) e (3) 
 g 
 Xét mô hình một nhà máy thủy điện đơn giản như hình xe (s) 1 s.Tg
 1, sơ đồ khối tương ứng như hình 2. Mỗi hệ thống thủy điện 
 Trong đó, Tg là hằng số thời gian servo chính (giây). 
 đơn vùng bao gồm các thành phần cơ bản như: máy phát 
 Hình 3 mô tả đáp ứng quá độ của hàm truyền đạt được 
 điện, tuabin thủy lực và bộ điều tốc. Để điều khiển lưu 
 cho trong (3) khi T thay đổi ở một vài giá trị. 
 lượng nước cấp làm quay tuabin thủy lực qua đó ổn định g 
 tốc độ và tần số của máy phát, người ta tiến hành điều 
 khiển góc mở van cánh hướng (hình 2). 
 Hình 1. Mô hình nhà máy thủy điện 
 Hình 3. Mô phỏng đặc tính làm việc của bộ điều tốc khi Tg thay đổi 
 Bước 3: Xây dựng mô hình tuabin thủy lực 
 Hàm truyền đạt mô tả mối quan hệ giữa sự thay đổi công 
 suất đầu ra của tuabin và sự thay đổi vị trí cánh hướng đầu vào 
 tuabin thủy lực là: 
 Pm (s) 1 T s
 w (s) w (4) 
 t 1 0,5T s
 Hình 2. Mô hình khối của hệ thống thủy điện đơn vùng g(s) w
30 Tạp chí KHOA HỌC VÀ CÔNG NGHỆ ● Tập 56 - Số 3 (6/2020) Website: https://tapchikhcn.haui.edu.vn 
P-ISSN 1859-3585 E-ISSN 2615-9619 SCIENCE - TECHNOLOGY 
 Phương trình (4) có thể được coi là hàm truyền đạt của 
tuabin thủy lực kết hợp đường ống áp lực trong trường hợp 
lý tưởng. Hàm truyền đạt này rõ ràng phụ thuộc và TW. Kết 
quả đáp ứng quá độ của độ thay đổi công suất cơ đầu ra 
tuabin phụ thuộc vào các giá trị khác nhau của Tw là hằng 
số thời gian khởi động của nước với tải bất kì được thể hiện 
trên hình 4. 
 Hình 7. Đáp ứng quá độ của đặc tính máy phát - phụ tải 
 2.2. Mô hình toán học nhà máy thủy điện đơn vùng 
 Từ phần trên, tổng hợp lại ba bước xây dựng mô hình 
 của nhà máy thủy điện đơn vùng ta có thể xây dựng mô 
 hình tổng quát như hình 8. Hàm truyền đạt của từng khối 
 trong mô hình đơn vùng này đã được thành lập ở phần 
 trên. Các tham số mô phỏng cho mô hình được cho trong 
 Hình 4. Mô phỏng đặc tính làm việc của tuabin khi T thay đổi 
 w phần phụ lục của bài báo. 
 Mô hình máy phát điện 
 Trong [1] ta có mô hình máy phát điện đồng bộ sử dụng 
động năng của tuabin để chuyển đổi thành điện năng 
(hình 5) được biểu diễn như sau: 
 (s) 1
 wp (s) (5) 
 Pm (s) P e (s) Ms D
 Trong đó, ω() s : giá trị chuẩn hóa của độ lệch của tốc 
độ máy phát (p.u.), Pe : giá trị chuẩn hóa của độ lệch công 
suất tải (p.u.), D: hằng số thời gian tắt dần của phụ tải đặc 
trưng cho phụ thuộc tần số trong lưới điện, M: momen 
quán tính tổng của máy phát (MW). Hình 6 biểu diễn mối Hình 8. Mô hình hệ thống điều khiển tốc độ tuabin thủy điện đơn vùng 
quan hệ giữa đầu vào và đầu ra của máy phát điện đồng bộ 
đã cho bởi công thức (5). Đáp ứng quá độ của hàm truyền 
đạt máy phát - phụ tải với các giá trị khác nhau của M và D 
được thể hiện trên hình 7. 
 Hình 5. Mạch vòng điều khiển tần số 
 Hình 9. Đáp ứng các khâu của sơ đồ hệ thống thủy điện đơn vùng 
 Trên hình 9 ta thấy, từ 0 đến 10s ta chưa kích tín hiệu 
 cho điều tốc do vậy hệ thống vẫn ổn định, khoảng 10s ta 
 kích tín hiệu từ 0 lên 1 lúc đó đầu ra của bộ điều tốc, van 
 cách hướng bắt đầu mở dần ΔXe đồng thời công suất trên 
 trục tuabin ΔPm cũng tăng. Thời gian 10s đến 20s tốc độ 
 Hình 6. Mô hình máy phát điện tuabin Δω tăng dần theo độ mở cánh hướng. Khi được 20s 
 Website: https://tapchikhcn.haui.edu.vn Vol. 56 - No. 3 (June 2020) ● Journal of SCIENCE & TECHNOLOGY 31
 KHOA H ỌC CÔNG NGHỆ P - ISSN 1859 - 3585 E - ISSN 2615 - 961 9 
 ta đóng tải ΔPL bằng 50% lúc đó tốc độ tuabin sẽ giảm. Để 2π
 P()()() s F s F s (11) 
 đáp ứng đầu ra ổn định ta có thể thiết kế bộ điều khiển để tiei, js i j 
 điều khiển làm cho tốc độ luôn ổn định khi tải thay đổi. 
 Trong [1] mô hình toán học của hệ thống thủy điện liên 
 2.3. Mô hình hệ thống thủy điện liên kết hai vùng kết hai vùng có cấu trúc trên hình 11. 
 Trong thực tế, các hệ thống điện thường không tồn tại 
 riêng lẻ, mà chúng thường liên kết với nhau tạo nên hệ 
 thống điện lớn. Khi đó sẽ hình thành khái niệm vùng (thực 
 chất là một nhà máy phát điện độc lập tương đối, có trao 
 đổi công suất với các nhà máy phát điện khác). Hình 10 mô 
 tả một hệ thống thủy điện liên kết hai vùng điển hình. 
 a) Hình 11. Mô hình hệ thống điều khiển tuabin thủy điện có liên kết 2 vùng 
 Từ mô hình toán học ta khảo sát đặc tính của các khối 
 chức năng của hệ thống thủy điện liên kết hai vùng khi 
 chưa có bộ điều khiển như hình 12. 
 b) 
 Hình 10. Hệ thống điện liên kết hai khu vực 
 Trong hình 10, tie-line là một đường truyền tải điện 
 năng kết nối hai khu vực điều khiển. Trong [2], công suất 
 trao đổi từ khu vực 1 đến khu vực 2 được tính như sau: 
 VV1  2 
 Ptie1,2 sin(  1  2 ) (6) 
 X12
 trong đó, δ1 và δ2 là các góc của điện áp cuối lần lượt 
 là [V1] và [V2]. Đối với độ lệch nhỏ, các góc và công suất Hình 12a. Đáp ứng của vùng 1khi chưa có bộ điều khiển 
 đường dây cũng thay đổi với một lượng nhỏ. Công suất 
 đường dây tăng dần từ khu vực 1 đến khu vực 2 có thể được Trên hình 12a ta thấy, từ 0 - 10s khi chưa có tín hiệu điều 
 biểu thị bằng: khiển cho điều tốc nên chưa xuất hiện dao động. Tuy 
 nhiên, khoảng 10s sau ta kích thích tín hiệu điều khiển điều 
 ()   (7) 
 PTtie1, 2 12 1 2 tốc từ 0 lên 1 lúc đó đầu ra của bộ điều tốc là độ mở van 
 cánh hướng ΔX bắt đầu mở dần, đồng thời công suất trục 
 Trong đó, T12 là hệ số công suất đồng bộ hóa trên e
 đường dây. tuabin ΔPm1 tăng dẫn đến công suất đầu ra máy phát ΔPGen1 
 và ΔPtie1 công suất trên đường dây cũng thay đổi liên tục. 
 VV1  2 
 T12 cos(  1  2 ) (8) Tiếp theo thời gian từ 10s đến 20s tốc độ tuabin Δω1 và độ 
 X12 mở cánh hướng cũng tăng dần. Khi được 20s ta đóng 50% 
 Tần số tăng có liên quan đến độ lệch góc pha như được tải ΔPL1 vào lúc đó tốc độ tuabin sẽ giảm, công suất máy 
 biểu thị bởi: phát ΔPGen1và công suất trên đường dây ΔPtie1 dao động rất 
 mạnh; tuy nhiên do độ mở cánh hướng tăng sau thời gian 
 δ 2π Fdt và δ 2 π f dt (9) 
 1 1 2 2 khoảng 40s thì công suất và tốc độ dần ổn định. 
 Sau đó phương trình (9) trở thành: Trên hình 12b ta thấy từ 0 - 15s chưa có tín hiệu điều 
 2πT khiển cho điều tốc nên chưa xuất hiện dao động, tuy nhiên 
 P (s) 12  F(s) F(s)  (10) khoảng 15s sau ta kích thích tín hiệu điều khiển điều tốc từ 
 tie1,2s 1 2
 0 lên 1 lúc đó đầu ra của bộ điều tốc là van cánh hướng ΔXe 
 Bằng cách thực hiện phép biến đổi Laplace của phương bắt đầu mở dần, đồng thời công suất trục tuabin ΔPm2 tăng 
 trình (10) công suất đường dây được thể hiện như sau: dẫn dẫn đến công suất đầu ra máy phát ΔPGen2 và ΔPtie2 
32 Tạp chí KHOA HỌC VÀ CÔNG NGHỆ ● Tập 56 - Số 3 (6/2020) Website: https://tapchikhcn.haui.edu.vn 
P-ISSN 1859-3585 E-ISSN 2615-9619 SCIENCE - TECHNOLOGY 
công suất trên đường dây cũng thay đổi liên tục, tiếp theo Các vectơ B và D được coi là độc lập khi giả định rằng 
thời gian từ 15s đến 40s tốc độ tuabin Δω2 và độ mở cánh 
 vectơ phụ tải thay đổi bị chặn PPe c với Pc là một giá trị 
hướng cũng tăng dần. Khi được 40s ta đóng 50% tải ΔP12 
vào lúc đó tốc độ tuabin sẽ giảm, công suất máy phát chặn (là số thực dương cho trước). 
ΔPGen2 và công suất trên đường dây ΔPtie2 dao động rất 3. ĐIỀU KHIỂN ỔN ĐỊNH TỐC ĐỘ TUABIN NHÀ MÁY 
mạnh, tuy nhiên độ mở cánh hướng tăng sau thời gian THỦY ĐIỆN LIÊN KẾT VÙNG ỨNG DỤNG MÔ HÌNH TOÁN 
khoảng 60s thì công suất và tốc độ dần ổn định. HỌC ĐÃ XÂY DỰNG 
 Trong phần này, để làm rõ hiệu quả cũng như tính khả 
 thi của mô hình toán đã xây dựng cho bài toán ổn định tốc 
 độ tuabin thủy lực, ta xét một trường hợp mô phỏng điển 
 hình của hệ thống điện hai vùng liên kết khi có bộ điều 
 khiển. Mục tiêu của bài toán điều khiển tần số hệ thống 
 thủy điện liên kết vùng là dập tắt dao động của tần số lưới 
 cũng như công suất trao đổi trên đường dây khi phụ tải của 
 các vùng thay đổi. 
 Trong hình 11 sai lệch tần số và sai lệch công suất trao 
 đổi đường dây được kết hợp tạo thành tín hiệu điều khiển 
 sai lệch vùng ACE (Area Control Error). Các kết quả mô 
 phỏng theo sơ đồ này được thể hiện trên hình 13a và 13b. 
 Hình 12b. Đáp ứng của vùng 2 chưa có bộ điều khiển 
2.4. Mô hình không gian trạng thái của hệ thống thủy điện 
 Trong [2] dựa trên mô hình động của nhà máy thủy 
điện, có thể mô tả trạng thái của toàn bộ mô hình nhà máy 
tương ứng với hình 1 như sau: 
 T
 T t 
 x  x x x x x  ω ωe g p ω (12) 
 1 2 3 4 5 0 m 
 Tất cả các trạng thái này có thể được đo lường dễ dàng. 
Do đó, việc thiết kế bộ điều khiển phản hồi trạng thái có thể 
được thực hiện dễ dàng. Phương trình trạng thái hệ thống: 
 ̇= Ax +Bu+DP. (13) 
 e a) 
 Trong đó: 
 0 0 0 0 1 
 1 1 
 0 0 0 
 TTRP p p 
 1 1 
 A 0 0 0 ;
 TTp p 
 2 2 2 2
 0 () 0 
 TTTTgw g w 
 1 d
 0 0 0 
 m m 
 0 b) 
 Hình 13. Đặc tính của hệ thống thủy điện liên kết hai vùng sử dụng bộ điều 
 1 0
 khiển tích phân 
 Tp 0 
 B 0 và D 0 (14) Quan sát trên hình 13a của vùng 1, khi chưa sử dụng bộ 
 điều khiển cho thấy từ 0 đến 20s ta đóng 50% tải vào. Sau 
 0 0 đó quan sát trên hình 13a ta thấy, ΔP và ΔP dao động 
 Gen1 tie1
 0 1 rất mạnh quá trình quá độ lớn hơn 40% và cho đến 40s sau 
 m chúng dần về không, tuy nhiên hệ thống không ổn định 
 được sai lệch tĩnh rất lớn khoảng 10%, còn khi ta sử dụng 
 Website: https://tapchikhcn.haui.edu.vn Vol. 56 - No. 3 (June 2020) ● Journal of SCIENCE & TECHNOLOGY 33
 KHOA H ỌC CÔNG NGHỆ P - ISSN 1859 - 3585 E - ISSN 2615 - 961 9 
 bộ điều khiển tích phân để điều khiển cho vùng 1 thì đến 
 40s các ΔPGen1 và ΔPtie1 giảm dần về không cho đến 80s thì TÀI LIỆU THAM KHẢO 
 công suất máy phát và công suất trên đường dây được triệt 
 [1]. Kundur P., 1994. Power system stability and control. New York, USA: 
 tiêu sai lệch tĩnh và ổn định về không. Do vậy khi ta sử 
 McGraw-Hill. 
 dụng bộ điều khiển tích phân để điều khiển tuabin máy 
 phát cho vùng 1 kết quả cho chất lượng tốt hơn rất nhiều [2]. Xibei Ding and Alok Sinha, 2011. Sliding Mode/H∞ Control of a Hydro-
 khi chưa sử dụng bộ điều khiển tích phân. power Plant American Control Conference on O'Farrell Street. San Francisco, CA, 
 USA June 29 - July 01. 
 Ta quan sát trên hình 13b và 12b cho vùng 2. Khi chưa 
 sử dụng bộ điều khiển ta thấy từ 0 đến 40s ta đóng 30% tải [3]. Shiva C.K., Mukherjee V., 2015. Automatic generation control of 
 interconnected power system for robust decentralized random load disturbances 
 vào sau đó quan sát trên hình 13b ta thấy ΔPGen2 và ΔPtie2 
 dao động rất mạnh quá trình quá độ lớn hơn 40% và cho using a novel quasi-oppositional harmony search algorithm. Int. J. Electr. Power 
 đến 40s sau chúng dần về không. Tuy nhiên hệ thống Energy Syst. 73, 991-1001. 
 không ổn định được sai lệch tĩnh rất lớn khoảng 10%, còn [4]. Dhillon S.S., Lather J.S., Marwaha S., 2015. Multi area load frequency 
 khi ta sử dụng bộ điều khiển tích phân để điều khiển cho control using particle swarm optimization and fuzzy rules. Procedia Comput. Sci. 
 vùng 2 thì đến 40s các ΔPGen2 và ΔPtie2 giảm dần về không; 57, 460-472. 
 cho đến 80s thì công suất máy phát và công suất trên [5]. C. Concordia and L. K. Kirchmayer, 1953. Tie line power and frequency 
 đường dây được triệt tiêu sai lệch tĩnh và ổn định về không. control of electric power systems. Amer. Inst. Elect. Eng. Trans., vol. pt. II,72, pp. 
 Do vậy khi ta sử dụng bộ điều khiển tích phân để điều 562 -572. 
 khiển tuabin máy phát cho vùng 2 kết quả cho chất lượng [6]. Liu X., Kong X., Lee K.Y., 2016. Distributed model predictive control for 
 tốt hơn rất nhiều khi chưa sử dụng bộ điều khiển tích phân. load frequency control with dynamic fuzzy valve position modelling for hydro-
 4. KẾT LUẬN thermal power system. IET Control Theory Appl. 10, 1653-1664. 
 Bài báo này trình bày về mô hình toán học của hệ thống [7]. Bhatti T., 2014. AGC of two area power system interconnected by AC/DC 
 điều khiển tuabin thủy điện liên kết vùng. Từ các quá trình links with diverse sources in each area. Int. J. Electr. Power Energy Syst. 55, 297-
 vật lý của hệ thống, ta tiến hành khảo sát các khâu và xây 304. 
 dựng cấu trúc hệ thống; tiếp theo mô phỏng các khối chức 
 năng như tuabin thủy điện liên kết vùng, điều tốc, máy 
 AUTHORS INFORMATION 
 phát cho từng vùng. Kết quả cho ta thấy khi chưa áp dụng 
 1 1 2
 bộ điều khiển tích phân cho chất lượng kém hơn rất nhiều Nguyen Duy Trung , Nguyen Ngoc Khoat , Hoang Thi Thu Huong , 
 3 4 4 
 khi hệ thống được sử dụng bộ điều khiển tích phân. Mô ĐàoThi Mai Phuong , Le Hung Lan , Nguyen Van Tiem 
 hình toán học đưa ra là phù hợp cho bài toán điều khiển 1Faculty of Control and Automation, Electric Power University 
 tần số thủy điện liên kết vùng, khi sử dụng bộ điều khiển 2Power Project Management Broad 2, Vietnam Electricity Corporation 
 tích phân sẽ triệt tiêu được sai lệch tĩnh của hệ thống và rất 3Faculty of Electrical Engineering, Hanoi University of Industry 
 ổn định phù hợp với yêu cầu đề ra. 
 4Department of Cybernetics, University of Transport and Communication 
 Hướng phát triển tiếp theo của báo cáo là tối ưu hóa hệ 
 thống phức hợp và áp dụng các thuật toán điều khiển 
 thông minh để ổn định tần số hệ thống đa liên kết trên 
 diện rộng của hệ thống. 
 PHỤ LỤC 
 1. Thông số mô phỏng cho mô hình hệ thống thủy điện 
 đơn vùng 
 Tg1 = 0,2s; Tw1 = 1,0s; M1 = 6,0s; D1 = 1,0; R1 = 5% 
 2. Thông số cho mô hình hệ thống thủy điện hai vùng 
 liên kết (đồng nhất) 
 T = 0,2s; T = 1,0s; M = 6,0s; D = 1,0; R = 5% 
 g1 w1 1 1 1 
 T = 0,2s; T = 1,0s; M = 6,0s; D = 1,0; R = 5%; 
 g2 w2 2 2 2 
 T12 = 0,0707 
34 Tạp chí KHOA HỌC VÀ CÔNG NGHỆ ● Tập 56 - Số 3 (6/2020) Website: https://tapchikhcn.haui.edu.vn