Nghiên cứu khả năng phát hiện tấn công tuyến tính trong các hệ thống điều khiển công nghiệp bằng phương pháp cusum

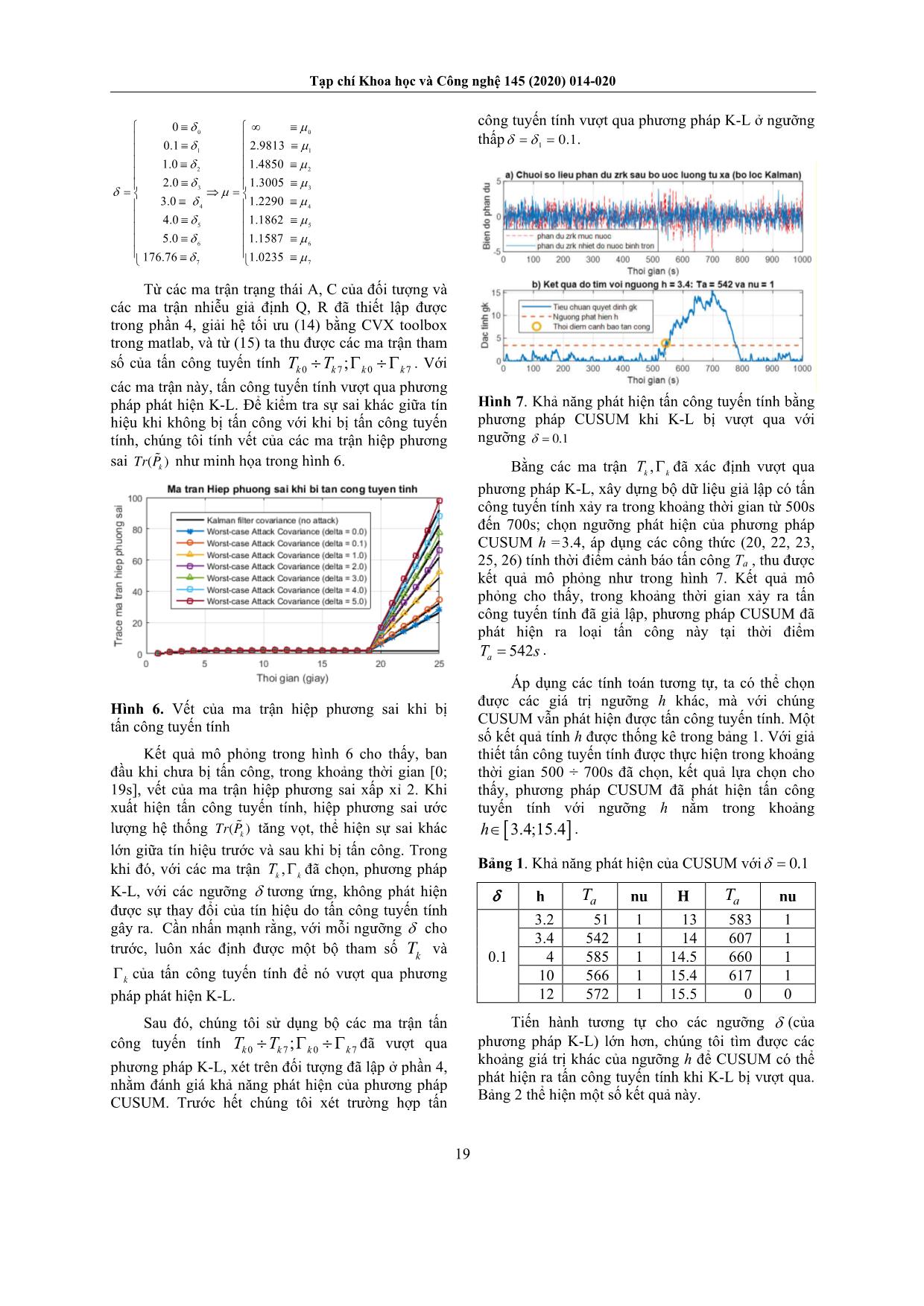
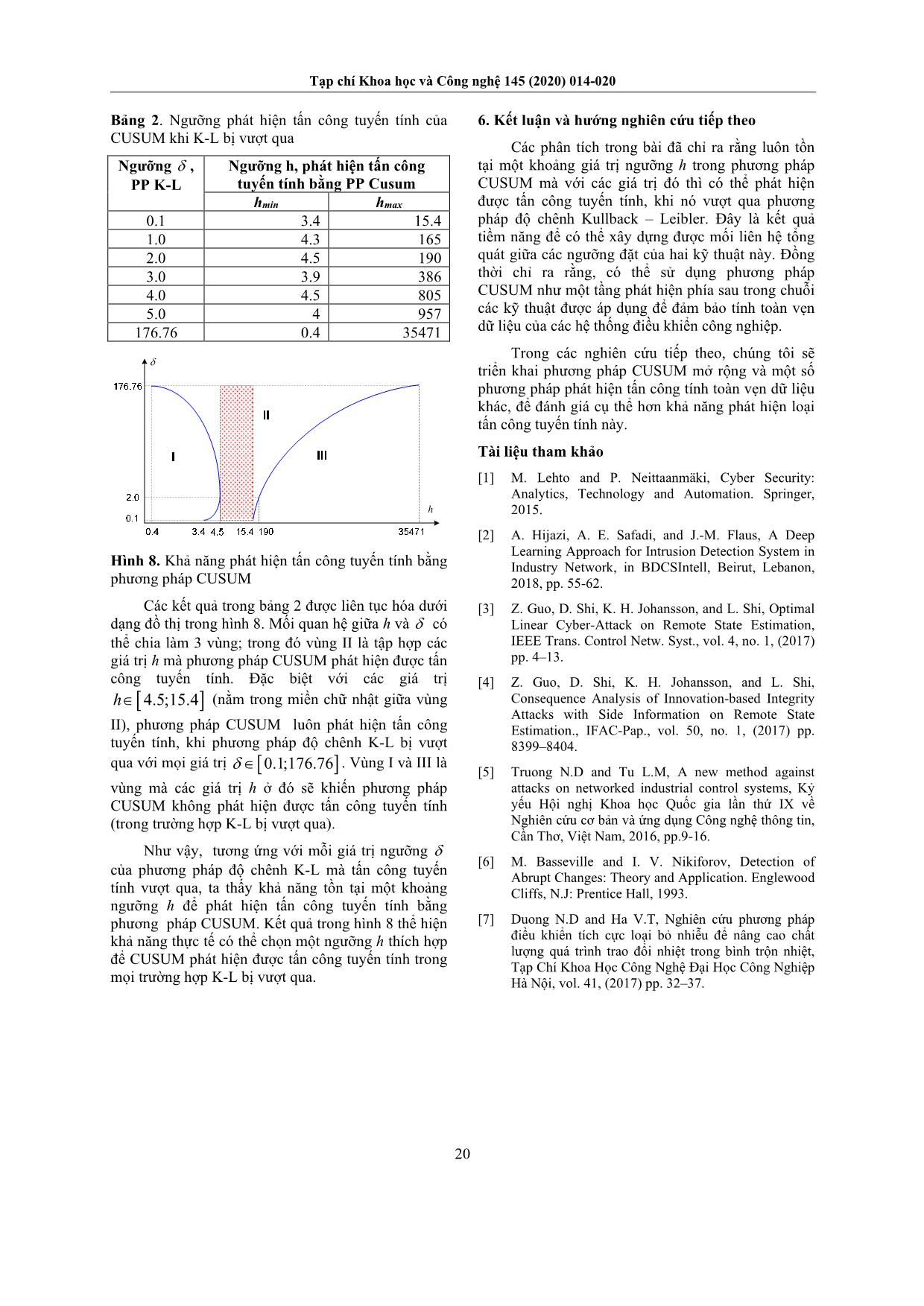
với kTr P là vết của ma trận hiệp phương sai khi dữ 
liệu bị tấn công. Trong đó ma trận 
k
P được tính như 
công thức (11) [4]: 
1  
  T T T T T
k k k k kP AP A Q K K PC T K KT CP 
(11) 
Theo [4], ta có nghiệm tối đa *
k
z của (10), thỏa mãn: 
1
1 2 T
k
K K

   

(12) 
với 
1
m in2 
i m
i 
và 
1 2
, ,...,
m
   là các giá trị riêng của TK K 
Theo quy hoạch lồi Karush Kuhn Tucker, từ 
(12), ta có mối quan hệ giữa ngưỡng à v  : 
 11 1 log 0
2 2 2
k
k
m
Tr  
 
   
 

 
(13) 
Ma trận 
k
T thỏa mãn (10) được xác định từ việc 
giải phương trình tối ưu quy hoạch lồi (14): 
 1
( )
1
min 
0 
T
k
Tk
k
T
k
Tr CPPC T
T
T
 
 
 

(14) 
và ma trận
k
 được xác định từ mối quan hệ: 
   T
k k k k
T T
(15) 
Như vậy, với mỗi ngưỡng  của phương pháp 
K-L đều có thể tìm ra các ma trận tấn công ,
k k
T  . 
Hay nói cách khác, luôn tồn tại khả năng để tấn công 
tuyến tính có thể vượt qua phương pháp phát hiện sai 
lệch dữ liệu K-L. 
3. Tổng quan phương pháp CUSUM 
Phương pháp CUSUM có khác biệt so với 
phương pháp K-L ở điểm là phương pháp này áp 
dụng lý thuyết Wald phân tích tính bất thường trong 
dữ liệu [6]. Đây là cơ sở để nghiên cứu khả năng phát 
hiện tấn công tuyến tính của phương pháp CUSUM. 
kx
Q
u
a
n
 s
á
t
k0k
0
0
0k T k
0
0k 1
1 
k
k
S
k
 1
 k k kg g s
1
kS
kg
 
0
kx P
 
1
kx P
1 1min 
i
i k S
Hình 3. Minh họa phương pháp CUSUM phát hiện 
dữ liệu bị tấn công 
Xét hệ ngẫu nhiên   1 2, ,... ,
T
k
X x x x N   . 
Giả sử khi chưa bị tấn công thì 0,X N   và 
khi bị tấn công thì 1, .X N   Ý tưởng của 
phương pháp CUSUM là tính đến tỷ lệ thay đổi thực 
Tạp chí Khoa học và Công nghệ 145 (2020) 014-020 
17 
sự 
i
S (likelihood ratio – LLR), (như được minh họa ở 
Hình 3), xác định theo công thức (16) [6]: 
1 1
0 0
ln ; S ln
 
k
i tk
i i
t i
i t
f x f x
S
f x f x
 
 
 (16) 
với 
1
 là chỉ số các điểm khi có thay đổi bất thường, 
0
 là chỉ số các điểm khi không có thay đổi bất 
thường. 
Theo cách định nghĩa, Si có xu hướng biến thiên 
đơn điệu khi không có thay đổi bất thường trong tín 
hiệu, và đổi chiều biến thiên tại thời điểm xảy ra thay 
đổi bất thường. 
Tiêu chuẩn để xác định dữ liệu có bị tấn công 
hay không được tính như công thức (17): 
1
1 0
0
ln , g =0
k
k k
k
f x
g g
f x


 (17) 
với max 0,
 x x (18) 
Theo phân bố chuẩn nhiều chiều (Multivariate 
Gaussian Distribution), ta có hiệp phương sai khi 
không có tấn công: 
0 0
1
12
0 0
, ,
1 1
det exp
22
 
   
n
T
P X P x
x x

 
 (19) 
với 
0
det là định thức của ma trận 0 , được tính như 
công thức (20): 
0  
TCPC R (20) 
Hiệp phương sai khi bị tấn công được viết dạng: 
1 1
1
12
1 1
, ,
1 1
det exp
22
n
T
P X P x
x x

 
 
   
 (21) 
với 
1
det là định thức của ma trận 1 , được tính như 
công thức (22): 
1 .  
T
k k kT T (22) 
Và do đó, tỷ lệ thay đổi (LLR) tính được theo công 
thức (23): 
 1 10 1 0
1
det1 1
ln
2 det 2
T
k
s x x  

   
 (23) 
Các giá trị kg của phương pháp CUSUM được xác 
định theo nguyên tắc trong công thức (24): 
1 1
1
 if 0
0 if 0
k k k k
k
k k
g s g s
g
g s
 (24) 
Từ (24) và (18), ta có: 
 1ax 0,k k kg m g s (25) 
và thời điểm cảnh báo tấn công Ta được xác định từ 
điều kiện: 
 min :a kT k g h (26) 
Trong đó h là ngưỡng phát hiện tấn công (đặt trước) 
theo phương pháp CUSUM. 
4. Đối tượng mô phỏng 
Trong bài báo này, chúng tôi xét mô hình tổng 
quát của quá trình trộn nhiệt trong các nhà máy sản 
xuất thực phẩm nói chung. Sơ đồ công nghệ của quá 
trình này được minh họa như trong hình 4. 
Hình 4. Sơ đồ công nghệ hệ thống bình trộn nhiệt 
1 1,F T 2 2,F T
3 3,F T
Hình 5. Sơ đồ đơn giản hóa bình trộn nhiệt 
Các thông số và các biến quá trình của mô hình 
bao gồm: 
F1 : lưu lượng của nước nóng (m3/h) 
F2 : lưu lượng của nước bổ sung (m3/h) 
F3 : lưu lượng của nước sau trộn (m3/h) 
1
T : nhiệt độ của nước nóng (oC) 
2
T : nhiệt độ của nước bổ sung (oC) 
3
T : nhiệt độ của nước trong bình trộn (oC) 
H : chiều cao mức nước bình trộn nhiệt; Hmax = 2.8 (m) 
ρ : khối lượng riêng của nước; ρ=1000 (kg/m3) 
V : thể tích lượng nước trong bình trộn nhiệt 
L : chiều dài bình trộn nhiệt; L = 14,5 (m) 
R : bán kính của bình; R = 1,4 (m) 
Nguyên lý hoạt động của quá trình là trộn dòng 
nước nóng qua van điều khiển CV1, SV1 với dòng 
nước lạnh qua van điều khiển CV2, SV2 để nước 
trong bình trộn có nhiệt độ mong muốn. Nước từ bình 
trộn cấp tới các nồi nấu thông qua van CV3 và SV3. 
Như vậy, có thể đơn giản hoá các thành phần của 
Tạp chí Khoa học và Công nghệ 145 (2020) 014-020 
18 
bình trộn nhiệt mà không làm sai lệch nguyên lý hoạt 
động của quá trình đã chọn, ta có sơ đồ bình trộn 
nhiệt như minh họa trong hình 5. 
Từ mô hình hoạt động của hệ thống đã chọn, ta 
có biến thiên mực nước trong bình trụ tròn nằm 
ngang có thể xác định theo công thức (27) [7]: 
 1 2 3
1
dH
F F F
dt A
 (27) 
với 2 2 A L H R H
(28) 
Theo định luật bảo toàn năng lượng, biến thiên nhiệt 
độ nước trong bình trộn nhiệt có thể tính theo công 
thức: 
 3 1 1 2 2 3 1 2
1
dT
FT F T T F F
dt V
 (29) 
Từ (27) ta có phương trình sai phân của mức nước 
trong bình: 
1 2 3
1 1 1 
 H F F F
A A A
 (30) 
với 2 2 A L H R H (31) 
Từ (29) ta có phương trình sai phân của nhiệt độ nước 
trong bình trộn nhiệt: 
1 3 2 3 1
3 1 2 1
2 1 2
2 3
T T T T F
T F F T
V V V
F F F
T T
V V
 (32) 
với ký hiệu ngang trên (*) để chỉ giá trị của một biến 
tại điểm làm việc, ký hiệu ( *) biểu diễn biến chênh 
lệch so với giá trị tại điểm làm việc. 
Từ (30) và (32), ta có: 
2
1 2
3 12 3 1 3
3
3
1
1 2
2
1 1
0 0
0
-1
0 0 ΔF
A
 + ΔT
F F
0 ΔT
ρV ρV
 
 

H H FA A
F F
T FT T T TT V
u tx t V V
x t
A
B
(33) 
Do lưu lượng 
3
F và nhiệt độ 1 2 , T T là các đại 
lượng nhiễu quá trình, giả sử các đại lượng này không 
thay đổi trong suốt quá trình trộn tức là: 
3 1 2 = 0; = 0F T T , ta có: 
  x t Ax t Bu t (34) 
Giả sử rằng hai bộ cảm biến LT và TT3 được sử 
dụng để đo mức trong bình trộn nhiệt H(t) và nhiệt độ 
trong bình trộn 
3
( )T t . Ta có phương trình đo: 
1 1
2 32
0
0


x ty t C
y t HK
y t TK
(35) 
 1y t 
: tín hiệu đo mức bình trộn 
 2y t : tín hiệu đo nhiệt độ trong bình trộn 
Xét bình trộn nhiệt với các thông số: 
3
max max 1 2
3 1 2 3 max 1 2
160 / ; 0.5 ; 80 C ; 37 C
39 C; 0.5 ; 0.5; 0.7
O O
O
F m h H H T T
T F F F F K K
và chu kỳ lấy mẫu 0 .1
S
T s 
Từ (34) và (35) ta có mô hình trạng thái liên tục mô tả 
đối tượng: 
 

x t Ax t Bu t
y t Cx t
 (36) 
với 5
0 0 0.0308 0.0308
10 ; 
0 0.396 -0.1573 3.2253
 A B 
Từ (36), chuyển sang dạng gián đoạn, ta có mô hình 
trạng thái không liên tục của đối tượng: 
1
k k k
k k
x Ax Bu
y Cx
 (37) 
với 
1 0 0.0031 0.0031 0.5 0
; B ;
0 1 -0.0157 0.3225 0 0.7
A C 
Do ở đây ta không quan tâm tín hiệu điều khiển, 
giả sử 0 
k
u , đối tượng có thể mô tả dưới dạng 
phương trình (1) và (2). Trong đó, các ma trận hiệp 
phương sai của nhiễu trắng được chọn trong các mô 
phỏng của chúng tôi là: 
0.51 0 1 0
;
0 0.505 0 0.8
Q R 
5. Kết quả mô phỏng và thảo luận 
Trong phần này, chúng tôi thực hiện mô phỏng 
để đánh giá khả năng áp dụng phương pháp CUSUM 
phát hiện tấn công tuyến tính vào đối tượng được xây 
dựng trong phần 4. Trong đó, điểm mấu chốt là đánh 
giá khả năng tồn tại ngưỡng h để phương pháp vẫn có 
thể phát hiện dữ liệu bị tấn công khi phương pháp 
K-L bị vượt qua. 
Các công thức (12) và (13) cho biết mối quan hệ 
giữa  và  ở phương pháp K-L. Chọn các ngưỡng 
 ta tính được  . Về lý thuyết, ngưỡng 0 , song 
với giá trị lớn sẽ làm giảm độ nhạy của phương pháp, 
ngược lại các giá trị quá nhỏ sẽ gia tăng khả năng 
cảnh báo nhầm. Trong bài báo này, chúng tôi xét một 
số giá trị của trong phạm vi [0; 176.76].  
Tạp chí Khoa học và Công nghệ 145 (2020) 014-020 
19 
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
 0 
 0.1 2.9813 
 1.0 1.4850 
 2.0 1.3005 
 3.0 1.2290 
 4.0 1.1862 
 5.0 1.1587 
176.76 1.0235 
  
  
  
  
  
  
  
   
 
 
 
 
 
 
 
 
 
Từ các ma trận trạng thái A, C của đối tượng và 
các ma trận nhiễu giả định Q, R đã thiết lập được 
trong phần 4, giải hệ tối ưu (14) bằng CVX toolbox 
trong matlab, và từ (15) ta thu được các ma trận tham 
số của tấn công tuyến tính 
0 7 0 7;k k k kT T   . Với 
các ma trận này, tấn công tuyến tính vượt qua phương 
pháp phát hiện K-L. Để kiểm tra sự sai khác giữa tín 
hiệu khi không bị tấn công với khi bị tấn công tuyến 
tính, chúng tôi tính vết của các ma trận hiệp phương 
sai ( )kTr P
 như minh họa trong hình 6. 
Hình 6. Vết của ma trận hiệp phương sai khi bị 
tấn công tuyến tính 
Kết quả mô phỏng trong hình 6 cho thấy, ban 
đầu khi chưa bị tấn công, trong khoảng thời gian [0; 
19s], vết của ma trận hiệp phương sai xấp xỉ 2. Khi 
xuất hiện tấn công tuyến tính, hiệp phương sai ước 
lượng hệ thống ( )kTr P
 tăng vọt, thể hiện sự sai khác 
lớn giữa tín hiệu trước và sau khi bị tấn công. Trong 
khi đó, với các ma trận ,
k k
T  đã chọn, phương pháp 
K-L, với các ngưỡng  tương ứng, không phát hiện 
được sự thay đổi của tín hiệu do tấn công tuyến tính 
gây ra. Cần nhấn mạnh rằng, với mỗi ngưỡng  cho 
trước, luôn xác định được một bộ tham số 
k
T và 
k của tấn công tuyến tính để nó vượt qua phương 
pháp phát hiện K-L. 
Sau đó, chúng tôi sử dụng bộ các ma trận tấn 
công tuyến tính 0 7 0 7;k k k kT T   đã vượt qua 
phương pháp K-L, xét trên đối tượng đã lập ở phần 4, 
nhằm đánh giá khả năng phát hiện của phương pháp 
CUSUM. Trước hết chúng tôi xét trường hợp tấn 
công tuyến tính vượt qua phương pháp K-L ở ngưỡng 
thấp   1 0.1. 
Hình 7. Khả năng phát hiện tấn công tuyến tính bằng 
phương pháp CUSUM khi K-L bị vượt qua với 
ngưỡng 0.1 
Bằng các ma trận ,
k k
T  đã xác định vượt qua 
phương pháp K-L, xây dựng bộ dữ liệu giả lập có tấn 
công tuyến tính xảy ra trong khoảng thời gian từ 500s 
đến 700s; chọn ngưỡng phát hiện của phương pháp 
CUSUM h =3.4, áp dụng các công thức (20, 22, 23, 
25, 26) tính thời điểm cảnh báo tấn công Ta , thu được 
kết quả mô phỏng như trong hình 7. Kết quả mô 
phỏng cho thấy, trong khoảng thời gian xảy ra tấn 
công tuyến tính đã giả lập, phương pháp CUSUM đã 
phát hiện ra loại tấn công này tại thời điểm 
542aT s . 
Áp dụng các tính toán tương tự, ta có thể chọn 
được các giá trị ngưỡng h khác, mà với chúng 
CUSUM vẫn phát hiện được tấn công tuyến tính. Một 
số kết quả tính h được thống kê trong bảng 1. Với giả 
thiết tấn công tuyến tính được thực hiện trong khoảng 
thời gian 500 ÷ 700s đã chọn, kết quả lựa chọn cho 
thấy, phương pháp CUSUM đã phát hiện tấn công 
tuyến tính với ngưỡng h nằm trong khoảng 
 3.4;15.4h . 
Bảng 1. Khả năng phát hiện của CUSUM với 0.1 
Tiến hành tương tự cho các ngưỡng  (của 
phương pháp K-L) lớn hơn, chúng tôi tìm được các 
khoảng giá trị khác của ngưỡng h để CUSUM có thể 
phát hiện ra tấn công tuyến tính khi K-L bị vượt qua. 
Bảng 2 thể hiện một số kết quả này. 
 h aT nu H aT nu 
0.1 
3.2 51 1 13 583 1 
3.4 542 1 14 607 1 
4 585 1 14.5 660 1 
10 566 1 15.4 617 1 
12 572 1 15.5 0 0 
Tạp chí Khoa học và Công nghệ 145 (2020) 014-020 
20 
Bảng 2. Ngưỡng phát hiện tấn công tuyến tính của 
CUSUM khi K-L bị vượt qua 
Ngưỡng  , 
PP K-L 
Ngưỡng h, phát hiện tấn công 
tuyến tính bằng PP Cusum 
hmin hmax 
0.1 3.4 15.4 
1.0 4.3 165 
2.0 4.5 190 
3.0 3.9 386 
4.0 4.5 805 
5.0 4 957 
176.76 0.4 35471 

h
Hình 8. Khả năng phát hiện tấn công tuyến tính bằng 
phương pháp CUSUM 
Các kết quả trong bảng 2 được liên tục hóa dưới 
dạng đồ thị trong hình 8. Mối quan hệ giữa h và  có 
thể chia làm 3 vùng; trong đó vùng II là tập hợp các 
giá trị h mà phương pháp CUSUM phát hiện được tấn 
công tuyến tính. Đặc biệt với các giá trị 
 4.5;15.4h (nằm trong miền chữ nhật giữa vùng 
II), phương pháp CUSUM luôn phát hiện tấn công 
tuyến tính, khi phương pháp độ chênh K-L bị vượt 
qua với mọi giá trị  0.1;176.76 . Vùng I và III là 
vùng mà các giá trị h ở đó sẽ khiến phương pháp 
CUSUM không phát hiện được tấn công tuyến tính 
(trong trường hợp K-L bị vượt qua). 
Như vậy, tương ứng với mỗi giá trị ngưỡng  
của phương pháp độ chênh K-L mà tấn công tuyến 
tính vượt qua, ta thấy khả năng tồn tại một khoảng 
ngưỡng h để phát hiện tấn công tuyến tính bằng 
phương pháp CUSUM. Kết quả trong hình 8 thể hiện 
khả năng thực tế có thể chọn một ngưỡng h thích hợp 
để CUSUM phát hiện được tấn công tuyến tính trong 
mọi trường hợp K-L bị vượt qua. 
6. Kết luận và hướng nghiên cứu tiếp theo 
Các phân tích trong bài đã chỉ ra rằng luôn tồn 
tại một khoảng giá trị ngưỡng h trong phương pháp 
CUSUM mà với các giá trị đó thì có thể phát hiện 
được tấn công tuyến tính, khi nó vượt qua phương 
pháp độ chênh Kullback – Leibler. Đây là kết quả 
tiềm năng để có thể xây dựng được mối liên hệ tổng 
quát giữa các ngưỡng đặt của hai kỹ thuật này. Đồng 
thời chỉ ra rằng, có thể sử dụng phương pháp 
CUSUM như một tầng phát hiện phía sau trong chuỗi 
các kỹ thuật được áp dụng để đảm bảo tính toàn vẹn 
dữ liệu của các hệ thống điều khiển công nghiệp. 
Trong các nghiên cứu tiếp theo, chúng tôi sẽ 
triển khai phương pháp CUSUM mở rộng và một số 
phương pháp phát hiện tấn công tính toàn vẹn dữ liệu 
khác, để đánh giá cụ thể hơn khả năng phát hiện loại 
tấn công tuyến tính này. 
Tài liệu tham khảo 
[1] M. Lehto and P. Neittaanmäki, Cyber Security: 
Analytics, Technology and Automation. Springer, 
2015. 
[2] A. Hijazi, A. E. Safadi, and J.-M. Flaus, A Deep 
Learning Approach for Intrusion Detection System in 
Industry Network, in BDCSIntell, Beirut, Lebanon, 
2018, pp. 55-62. 
[3] Z. Guo, D. Shi, K. H. Johansson, and L. Shi, Optimal 
Linear Cyber-Attack on Remote State Estimation, 
IEEE Trans. Control Netw. Syst., vol. 4, no. 1, (2017) 
pp. 4–13. 
[4] Z. Guo, D. Shi, K. H. Johansson, and L. Shi, 
Consequence Analysis of Innovation-based Integrity 
Attacks with Side Information on Remote State 
Estimation., IFAC-Pap., vol. 50, no. 1, (2017) pp. 
8399–8404. 
[5] Truong N.D and Tu L.M, A new method against 
attacks on networked industrial control systems, Kỷ 
yếu Hội nghị Khoa học Quốc gia lần thứ IX về 
Nghiên cứu cơ bản và ứng dụng Công nghệ thông tin, 
Cần Thơ, Việt Nam, 2016, pp.9-16. 
[6] M. Basseville and I. V. Nikiforov, Detection of 
Abrupt Changes: Theory and Application. Englewood 
Cliffs, N.J: Prentice Hall, 1993. 
[7] Duong N.D and Ha V.T, Nghiên cứu phương pháp 
điều khiển tích cực loại bỏ nhiễu để nâng cao chất 
lượng quá trình trao đổi nhiệt trong bình trộn nhiệt, 
Tạp Chí Khoa Học Công Nghệ Đại Học Công Nghiệp 
Hà Nội, vol. 41, (2017) pp. 32–37.