Nghiên cứu công thức vector cường độ từ trường để tính toán sự phân bố của từ thông tản và dòng điện foucault trong bài toán điện động bằng phương pháp phần tử hữu hạn

ều được mô tả bởi hệ phương trình 
Maxwell cùng với các luật trạng thái. Đây 
là các phương trình đạo hàm riêng viết 
dưới dạng vi - tích phân, là liên kết giữa 
vectơ cường độ từ trường, mật độ từ cảm, 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
18 Số 23 
cường độ điện trường và vectơ từ thế 
thông qua các luật trang thái. Để giải 
được các phương trình đạo hàm riêng với 
các biến là các tham số về trường, các nhà 
nghiên cứu không thể thực hiện bằng 
phương pháp giải tích hoặc hoặc phương 
pháp mạch từ không gian thay thế [1], vì 
kích thước và số bậc tự do của ma trận rất 
lớn, đặc biệt khó đối với các bài toán có 
cấu trúc và hình dạng phức tạp. 
Do đó, để giải quyết được các bài toán 
này, những năm gần đây đã có nhiều tác 
giả sử dụng các phương pháp số để giải 
và phân tích, cụ thể như phương pháp 
phần tử hữu hạn, phương pháp sai phân 
hữu hạn, phương pháp tích phân số, 
phương pháp phần tử biên Trong đó, 
phương pháp phần tử hữu hạn [2] là một 
trong những phương pháp phổ biến nhất 
và phù hợp nhất để tính toán, phân tích và 
mô phỏng các hiện tượng điện từ xảy ra 
trong các thiết bị điện từ. 
Bài báo giới thiệu một nghiên cứu khai 
triển công thức vector cường độ từ trường 
ứng dụng phương pháp phần tử hữu hạn 
để tính toán sự phân bố của từ thông tản, 
từ thông rò và dòng điện Foucault trong 
mạch từ của thiết bị điện. Nhiều mô hình 
đã được thực hiện tương ứng với các 
trường hợp khác nhau về độ lớn của khe 
hở không khí. Sự phù hợp của phương 
pháp sẽ được minh họa thông qua bài toán 
thực tế. 
2. BÀI TOÁN ĐIỆN TỪ 
2.1. Phương trình Maxwell 
Xét mô hình bài toán điện được xác định 
trong miền nghiên cứu 𝛺, với biên 
𝜕𝛺 = 𝛤 = 𝛤h ∪ 𝛤e trong không gian hai 
chiều và ba chiều. Hệ phương trình 
Maxwell cùng với các luật trạng thái và 
các điều kiện biên được viết trong không 
gian ba chiều Eculidean 3 [4]-[9] là: 
curl 𝒆 = −𝜕𝑡𝒃, curl 𝒉 = 𝒋𝑠, div𝒃 = 0 
(1a-b-c) 
 Các luật trạng thái: 
𝒃 = 𝜇𝒉, 𝒋 = 𝜎𝒆 (2a-b) 
 Các điều kiện biên: 
𝒏 × 𝒉|Γℎ=0, 𝒏 × 𝒆|Γ𝑒=0 (3a-b) 
trong đó b là mật độ từ cảm (T), h là 
cường độ từ trường (A/m), 𝒆 là cường độ 
điện trường (V/m), 𝜇 là độ từ thẩm của 
vật liệu từ, 𝜎 là độ dẫn điện (S/m), 𝒋 mật 
độ dòng điện Foucault được xác định 
trong miền dẫn từ Ω𝑐 (Ω𝑐 ⊂ Ω); 𝒋𝑠 là mật 
độ dòng điện được đặt vào cuộn dây được 
xác định trong miền không dẫn từ Ω𝑐
𝐶, 
with Ω𝑐 = Ω𝑐 ∪ Ω𝑐
𝐶 và n là vectơ pháp 
tuyến đơn vị có hướng từ trong ra ngoài 
của miền Ω. 
Phương trình (1a) và (1b) được giải kết 
hợp với điều kiện biên xét đến thành phần 
tiếp tuyến của vectơ cường độ từ trường 
và điện trường được cho trong (3a) và 
(3b). 
Đối với bài toán từ động, các trường 
h, b, e, j sẽ được xác định và kiểm chứng 
ràng buộc thỏa mãn sơ đồ Tonti [4]. Điều 
đó có nghĩa rằng 𝒉 ∈ 𝑯ℎ (curl; Ω), 
𝒋 ∈ 𝑯ℎ (div; Ω ), 𝒆 ∈ 𝑯𝑒 (curl; Ω ) và 
𝒃 ∈ 𝑯𝑒 (div; Ω ). Trong đó 𝑯ℎ (curl; Ω) 
và 𝑯𝑒 (dive; Ω) là các không gian hàm 
chứa các điều kiện biên và các trường tồn 
tại trên các biên Γℎ và Γ𝑒 của miền nghiên 
cứu Ω. Do đó, sơ đồ Tonti của bài toán từ 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 19 
động sẽ được xác định theo biểu đồ dưới 
đây [3]: 
Hình 1. Sơ đồ Tonti [3] 
2.2. Phương trình rời rạc với công 
thức vectơ cường độ từ trường 
Phương trình yếu rời rạc cho vectơ cường 
độ từ trường h được thiết lập dựa vào hệ 
phương trình Maxwell (1a-b-c) và các 
luật trạng thái (2a-b) ở mục 2.1. 
Để thỏa mãn phương trình Ampere 
(1b), các trường 𝒉 ∈ 𝑯ℎ (curl; Ω), 
𝒋 ∈ 𝑯ℎ (div; Ω ), 𝒆 ∈ 𝑯𝑒 (curl; Ω ) và 
𝒃 ∈ 𝑯𝑒 (div; Ω ) phải được kiểm tra và 
thỏa mãn các luật trạng thái được cho 
trong (2a-b). Dựa vào định luật Faraday 
(1a), phương trình rời rạc được viết: 
∫ 𝜕𝑡(𝒃 ∙ 𝒉
′)𝑑Ω
𝛺
+ ∫ curl 𝒆 ∙ 𝒉′𝑑Ω
𝛺
= 0, 
∀ 𝒉′ ∈ 𝑯ℎ
0(curl; Ω) (4) 
trong đó trường 𝒉′ ∈ 𝑯ℎ
0(curl; Ω) là một 
trường của hàm thử “test function” không 
phụ thuộc vào thời gian. Áp dụng công 
thức Green cho công thức (4) với miền 
nghiên cứu Ω, ta có: 
∫ 𝜕𝑡(𝒃 ∙ 𝒉
′)𝑑Ω
𝛺
+ ∫ curl 𝒆 ∙ 𝒉′𝑑Ω
𝛺
+ ∫(𝒏 × 𝒉) ∙ 𝒉′𝑑Γ
Γ
= 0, 
∀ 𝒉′ ∈ 𝑯ℎ
0(curl; Ω) (5) 
Thay luật trạng thái ở phương trình (3a-b) 
và định luật Ohm vào phương trình (5), 
ta có: 
∫ 𝜕𝑡(𝜇𝒉 ∙ 𝒉
′)𝑑Ω
𝛺
+ ∫ 𝜎−1curl 𝒉 ∙ curl𝒉′𝑑Ω
𝛺
+ ∫ 𝒆 ∙ curl𝒉′𝑑Ω
𝛺
+ ∫(𝒏 × 𝒆) ∙ 𝒉′𝑑Γ
Γ
= 0. 
∀ 𝒉′ ∈ 𝑯ℎ
0(curl; Ω) (6) 
Cường độ điện trường 𝒉 trong miền 
nghiên cứu Ω trong (6) được xác định [5]: 
𝒉 = 𝒉𝑟 + 𝒉𝑠 (7) 
trong đó, 𝒉𝑠 là một trường nguồn được 
xác định thông qua mật độ dòng điện 
được bơm vào cuộn dây 𝒋𝑠 trong miền Ω𝑠, 
và 𝒉𝑟 là trường phản ứng (biến chưa biết) 
cần được xác định thông qua: 
{
curl 𝒉 = 𝒋𝑠 trong miền Ω𝑠
curl 𝒉 = 0 trong miền Ω𝑐
𝐶 − Ω𝑠 
 (8) 
với 
curl 𝒉 = 0 trong miền Ω𝑐
𝐶 (9) 
Trong miền không dẫn Ω𝑐
𝐶, trường nguồn 
𝒉𝑟 có thể được xác định thông qua một từ 
thế vô hướng 𝜙, đó là 𝒉𝑟 = −grad 𝜙. Từ 
thế 𝜙 trong miền không dẫn Ω𝑐
𝐶 là đa trị 
và được biến đổi thành đơn trị dựa trên 
các kỹ thuật cắt ∑ thông qua các lỗ của 
miền dẫn Ω𝑐 [4]. 
Trường 𝒉′ trong phương trình rời rạc (6) 
sẽ được lựa chọn trong một không gian 
con của 𝑯ℎ
0(curl; Ω), với curl 𝒉′ = 0 
trong miền Ω𝑐
𝐶, khi đó 𝒉′ = 𝒉′𝑟 + 𝒉′𝑠. 
Đại lượng tích phân thứ ba trong phương 
trình rời rạc (6) được xác định bằng 
không trong miền không dẫn Ω𝑐
𝐶. Do đó, 
kết hợp với phương trình (7), phương 
trình (6) trở thành: 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
20 Số 23 
∫ 𝜕𝑡(𝜇𝒉𝒓 ∙ 𝒉
′)𝑑Ω + ∫ 𝜕𝑡(𝜇𝒉𝒔 ∙ 𝒉
′)𝑑Ω
𝛺𝛺
+ ∫ 𝜎−1curl 𝒉𝒓 ∙ curl𝒉
′𝑑Ω
𝛺
+ ∫(𝒏 × 𝒆) ∙ 𝒉′𝑑Γ
Γ
= 0, 
∀ 𝒉′ ∈ 𝑯ℎ
0(curl; Ω), 
với curl 𝒉𝑟
′ = 0 trong miền Ω𝑐
𝐶 
và 𝒉′ = 𝒉′𝑟 + 𝒉′𝑠, (10) 
trong đó 𝑯ℎ
0(curl; Ω) được xác định trong 
miền nghiên cứu Ω và chứa đựng các 
hàm nội suy (hàm dạng) của trường 𝒉 
(trường được liên kết tới từ thế vô 
hướng 𝜙), cũng như là hàm thử 𝒉′. 
Thành phần tiếp tuyến của cường độ điện 
trường 𝒏 × 𝒆 trong phương trình (8) được 
xác định trên biên Γ𝑒 của miền nghiên cứu 
Ω và được xem như là một điều kiện biên 
đồng nhất “Nummann” và được cho ở 
phương trình (3b). 
2.3. Rời rạc hóa của trường h 
Trường h trong phương trình rời rạc trong 
(8) được rời rạc hóa theo các phần tử 
cạnh, với không gian hàm được xác định 
trong lưới của miền nghiên cứu Ω, đó là: 
ℎ = ∑ ℎ𝑒𝑠𝑒 ,
𝑒∈𝐸(Ω)
 (11) 
trong đó 𝐸(Ω) là tập hợp của tất cả các 
cạnh của miền Ω, 𝑠𝑒 là hàm nội suy cạnh 
được kết hợp với cạnh e và ℎ𝑒 là thông 
lượng của trường h dọc theo cạnh e. Ở 
đây, phần tử lưới sử dụng là các phần tử 
tam giác và tứ giác. Như đã phân tích ở 
trên, trường phản ứng 𝒉𝑟 = 0 trong miền 
không dẫn Ω𝑐
𝐶, do đó 𝒉𝑟 = −grad 𝜙. 
Do đó, từ thế vô hướng có thể được phân 
tích [4]: 
𝜙|Ω = 𝜙𝑐|Ω𝑐𝐶 + 𝜙𝑑|Τ𝑐𝑢𝑡 + 𝜙𝑑|Τ𝑡 = 
𝜙𝑐|Ω𝑐𝐶 + ∑ 𝜙𝑑|Τ𝑐𝑢𝑡 + ∑ 𝜙𝑑|Τ𝑡 ,
𝑖∈Τ𝑡𝑖∈𝑐𝑢𝑡
 (12) 
trong đó, các 𝜙𝑑|Τ𝑐𝑢𝑡 và 𝜙𝑑|Τ𝑡 là các điện 
thế vô hướng không liên tục, chỉ tồn tại và 
xuất hiện trong bài toán mô hình vỏ mỏng 
và miền không dẫn đa trị Ω𝑐
𝐶 [4]. Do đó, 
đối với mô hình bài toán từ động mà 
không kể đến hai trường hợp, các hàm rời 
rạc hóa của từ thế vô hướng sẽ không có 
mặt trong phương trình rời rạc. 
Kết hợp giữa (9) và (10), sự rời rạc hóa 
của trường 𝒉 − 𝜙 sẽ được viết lại như 
sau [5]: 
𝒉 = 𝒉𝑠 + ∑ ℎ𝑘𝑠𝑘,
𝑒∈𝐸(Ω𝑐)
+ ∑ 𝜙𝑐,𝑛𝑣𝑐,𝑛
𝑒∈𝑁(Ω𝑐
𝐶)
. (13) 
3. BÀI TOÁN ÁP DỤNG 
Xét một bài toán điện từ có cấu trúc hình 
học 2-D được cho như hình 2. Sức từ 
động trong cuộn dây là 100 (A.vòng), độ 
từ thẩm tương đối và độ dẫn điện trong 
mạch từ và nắp mạch từ lần lượt là 
𝜇𝑟 = 1000, 𝜎 = 10 S/m và tần số f = 50 Hz. 
Hình 2. Mô hình hình học bài toán 2-D 
Bài toán được kiểm tra với các khe hở 
không khí khác nhau. Mô hình chia lưới 
2-D được giới thiệu ở hình 3. Hình 4 mô 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 21 
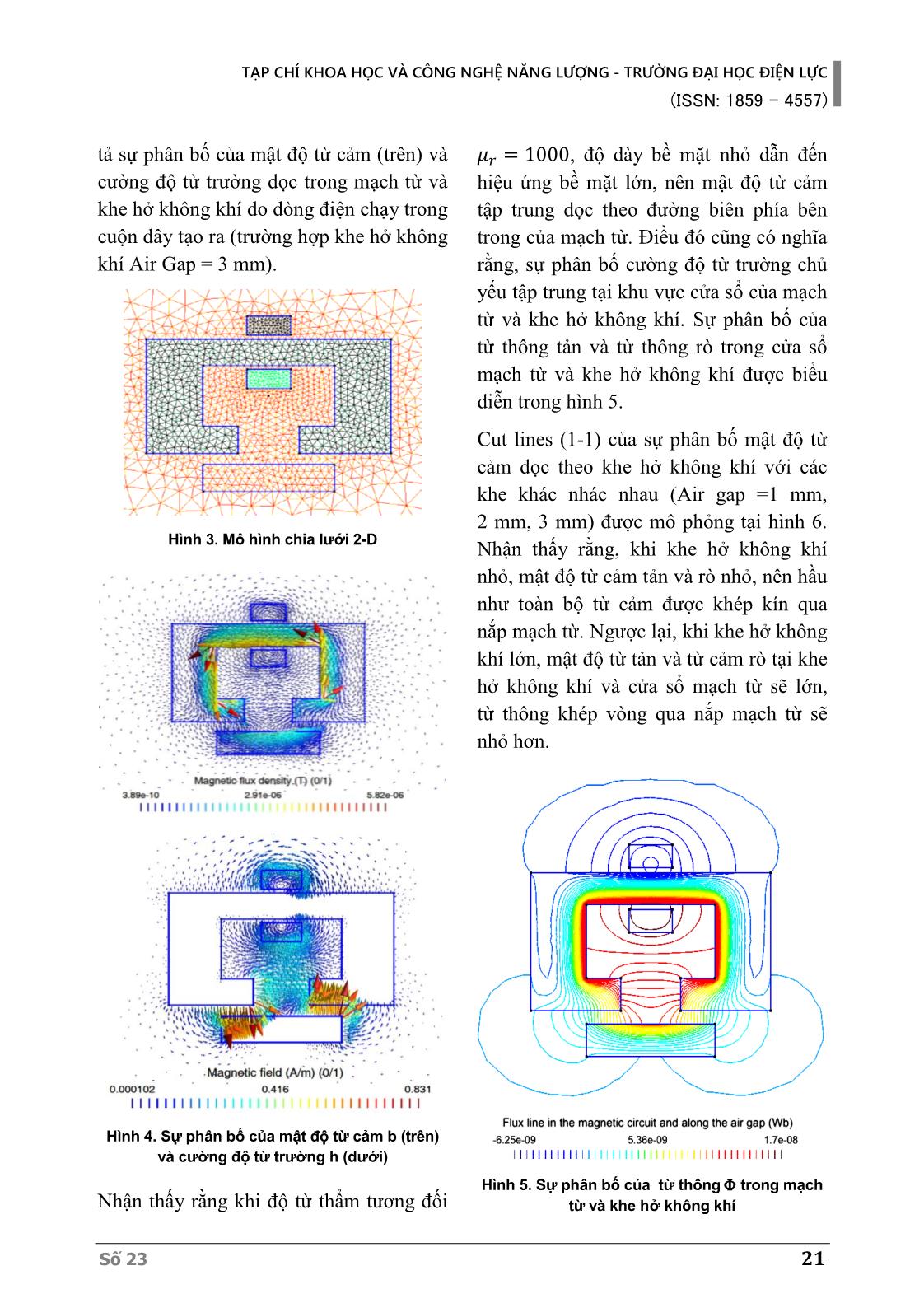
tả sự phân bố của mật độ từ cảm (trên) và 
cường độ từ trường dọc trong mạch từ và 
khe hở không khí do dòng điện chạy trong 
cuộn dây tạo ra (trường hợp khe hở không 
khí Air Gap = 3 mm). 
Hình 3. Mô hình chia lưới 2-D 
Hình 4. Sự phân bố của mật độ từ cảm b (trên) 
và cường độ từ trường h (dưới) 
Nhận thấy rằng khi độ từ thẩm tương đối 
𝜇𝑟 = 1000, độ dày bề mặt nhỏ dẫn đến 
hiệu ứng bề mặt lớn, nên mật độ từ cảm 
tập trung dọc theo đường biên phía bên 
trong của mạch từ. Điều đó cũng có nghĩa 
rằng, sự phân bố cường độ từ trường chủ 
yếu tập trung tại khu vực cửa sổ của mạch 
từ và khe hở không khí. Sự phân bố của 
từ thông tản và từ thông rò trong cửa sổ 
mạch từ và khe hở không khí được biểu 
diễn trong hình 5. 
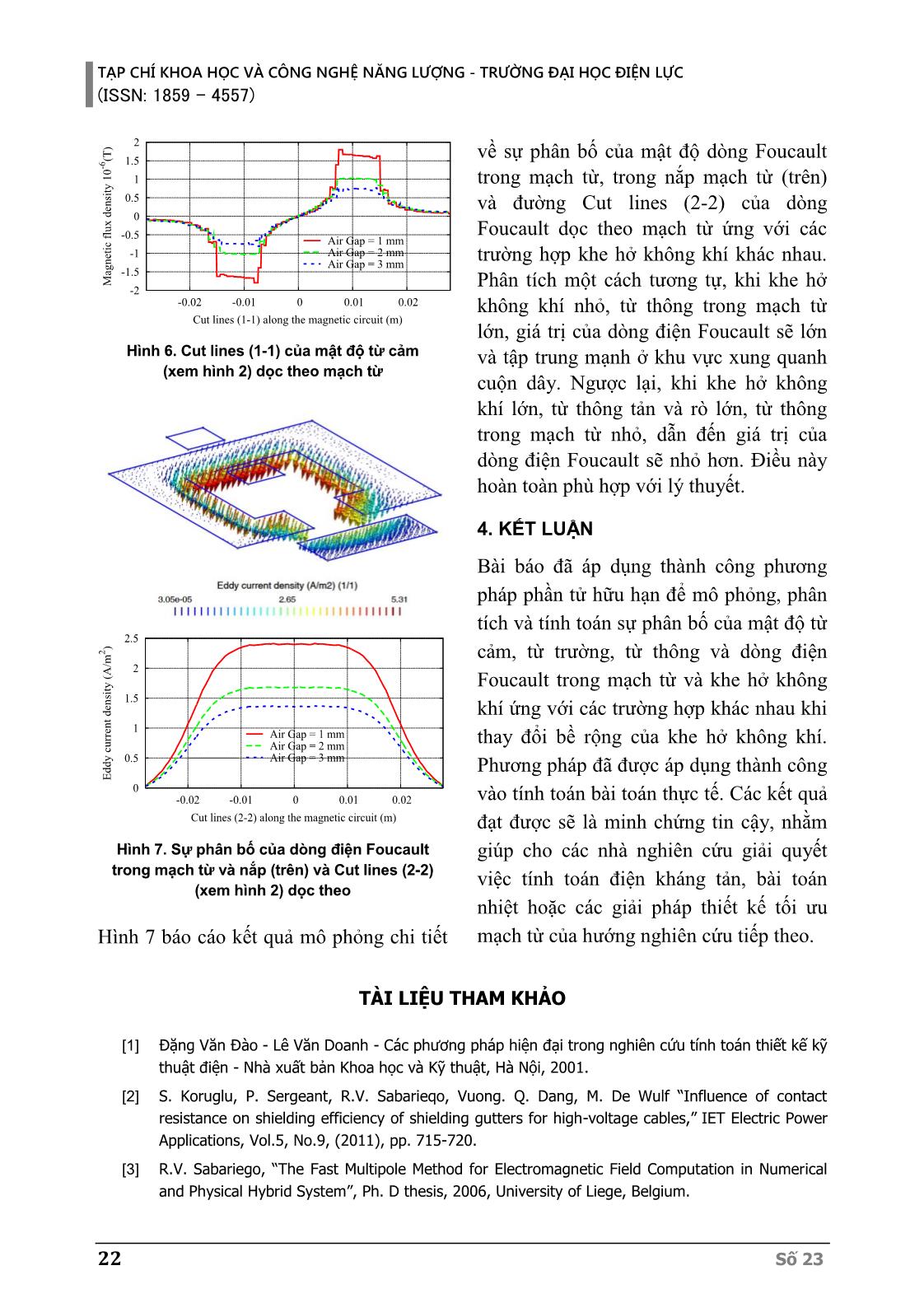
Cut lines (1-1) của sự phân bố mật độ từ 
cảm dọc theo khe hở không khí với các 
khe khác nhác nhau (Air gap =1 mm, 
2 mm, 3 mm) được mô phỏng tại hình 6. 
Nhận thấy rằng, khi khe hở không khí 
nhỏ, mật độ từ cảm tản và rò nhỏ, nên hầu 
như toàn bộ từ cảm được khép kín qua 
nắp mạch từ. Ngược lại, khi khe hở không 
khí lớn, mật độ từ tản và từ cảm rò tại khe 
hở không khí và cửa sổ mạch từ sẽ lớn, 
từ thông khép vòng qua nắp mạch từ sẽ 
nhỏ hơn. 
Hình 5. Sự phân bố của từ thông  trong mạch 
từ và khe hở không khí 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
22 Số 23 
Hình 6. Cut lines (1-1) của mật độ từ cảm 
(xem hình 2) dọc theo mạch từ 
Hình 7. Sự phân bố của dòng điện Foucault 
trong mạch từ và nắp (trên) và Cut lines (2-2) 
(xem hình 2) dọc theo 
Hình 7 báo cáo kết quả mô phỏng chi tiết 
về sự phân bố của mật độ dòng Foucault 
trong mạch từ, trong nắp mạch từ (trên) 
và đường Cut lines (2-2) của dòng 
Foucault dọc theo mạch từ ứng với các 
trường hợp khe hở không khí khác nhau. 
Phân tích một cách tương tự, khi khe hở 
không khí nhỏ, từ thông trong mạch từ 
lớn, giá trị của dòng điện Foucault sẽ lớn 
và tập trung mạnh ở khu vực xung quanh 
cuộn dây. Ngược lại, khi khe hở không 
khí lớn, từ thông tản và rò lớn, từ thông 
trong mạch từ nhỏ, dẫn đến giá trị của 
dòng điện Foucault sẽ nhỏ hơn. Điều này 
hoàn toàn phù hợp với lý thuyết. 
4. KẾT LUẬN 
Bài báo đã áp dụng thành công phương 
pháp phần tử hữu hạn để mô phỏng, phân 
tích và tính toán sự phân bố của mật độ từ 
cảm, từ trường, từ thông và dòng điện 
Foucault trong mạch từ và khe hở không 
khí ứng với các trường hợp khác nhau khi 
thay đổi bề rộng của khe hở không khí. 
Phương pháp đã được áp dụng thành công 
vào tính toán bài toán thực tế. Các kết quả 
đạt được sẽ là minh chứng tin cậy, nhằm 
giúp cho các nhà nghiên cứu giải quyết 
việc tính toán điện kháng tản, bài toán 
nhiệt hoặc các giải pháp thiết kế tối ưu 
mạch từ của hướng nghiên cứu tiếp theo. 
TÀI LIỆU THAM KHẢO 
[1] Đặng Văn Đào - Lê Văn Doanh - Các phương pháp hiện đại trong nghiên cứu tính toán thiết kế kỹ 
thuật điện - Nhà xuất bản Khoa học và Kỹ thuật, Hà Nội, 2001. 
[2] S. Koruglu, P. Sergeant, R.V. Sabarieqo, Vuong. Q. Dang, M. De Wulf “Influence of contact 
resistance on shielding efficiency of shielding gutters for high-voltage cables,” IET Electric Power 
Applications, Vol.5, No.9, (2011), pp. 715-720. 
[3] R.V. Sabariego, “The Fast Multipole Method for Electromagnetic Field Computation in Numerical 
and Physical Hybrid System”, Ph. D thesis, 2006, University of Liege, Belgium. 
-2
-1.5
-1
-0.5
 0
 0.5
 1
 1.5
 2
-0.02 -0.01 0 0.01 0.02
M
ag
n
et
ic
 f
lu
x
 d
en
si
ty
 1
0
-6
(T
)
Cut lines (1-1) along the magnetic circuit (m)
Air Gap = 1 mm
Air Gap = 2 mm
Air Gap = 3 mm
 0
 0.5
 1
 1.5
 2
 2.5
-0.02 -0.01 0 0.01 0.02
E
d
d
y
 c
u
rr
e
n
t 
d
e
n
si
ty
 (
A
/m
2
)
Cut lines (2-2) along the magnetic circuit (m)
Air Gap = 1 mm
Air Gap = 2 mm
Air Gap = 3 mm
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 23 
[4] Vuong Q. Dang, R.V. Sabariego, L. Krähenbühl, C. Geuzaine, “Subproblem Approach for 
Modelding Multiply Connected Thin Regions with an h-Conformal Magnetodynamic Finite Element 
Formulation,” in EPJ AP (Vol. 63, No.1, 2013). 
[5] P. Dular, R.V. Sabariego, M.V. Ferreira de Luz, P. Kuo-Peng and L. Krahenbuhl “Perturbation 
Finite Element Method for Magnetic Circuits”, IET Sci. Meas. Technol., 2008, Vol. 2, No.6, 
pp.440-446. 
[6] P. Dular, Vuong Q. Dang, R.V. Sabariego, L. Krähenbühl and C. Geuzaine, “Correction of thin 
shell finite element magnetic models via a subproblem method,” IEEE Trans. Magn., Vol. 47, no. 
5, pp. 158-1161, 2011. 
[7] Patrick Dular, Ruth V. Sabariego, Mauricio V. Ferreira de Luz, Patrick Kuo-Peng and Laurent 
Krahenbuhl “Perturbation Finite Element Method for Magnetic Model Refinement of - Air Gaps and 
Leakage Fluxes, Vol 45, No.3, 1400-1404, 2009. 
[8] Vuong Dang Quoc and Christophe Geuzaine “Using edge elements for modeling of 3-D 
Magnetodynamic Problem via a Subproblem Method”, Sci. Tech. Dev. J. ; 23(1) :439-445. 
[9] Dang Quoc Vuong and Nguyen Duc Quang, “Coupling of Local and Global Quantities by A 
Subproblem Finite Element Method - Application to Thin Region Models”, ISSN 1859-2171 - 
Advances in Science, Technology and Engineering Systems Journal (ASTESJ), Vol 4, no.2, 40-44 
(2019). 
Giới thiệu tác giả: 
Tác giả Đặng Quốc Vương nhận bằng Tiến sĩ chuyên ngành kỹ thuật điện năm 
2013 tại Đại học Liege, vương quốc Bỉ. Hiện tại tác giả là Giám đốc Trung tâm 
TCEE, giảng viên Viện Điện, Trường Đại học Bách khoa Hà Nội. 
Lĩnh vực nghiên cứu: Mô hình hóa hệ thống điện từ sử dụng mô hình các bài toán 
nhỏ - ứng dụng tới các thiết bị điện từ có cấu trúc mỏng (vỏ máy biết áp, tủ điện 
cao trung thế, màn chắn điện từ, lá thép kỹ thuật điện...); ứng dụng phương 
pháp số (phương pháp phần tử hữu hạn, phương pháp sai phân hữu hạn 
và phương pháp phần tử biên) tính toán ảnh hưởng của điện từ trường đến thiết bị điều khiển trong hệ 
thống điện; ứng dụng “subproblem method” tính toán thiết kế tối ưu hóa vật liệu trong thiết bị điện. 
Tác giả Nguyễn Đức Quang nhận bằng Tiến sĩ chuyên ngành kỹ thuật điện 2013 
tại Đại học Ecole Nationale Superieure d’Arts et Metiers Paristech, Pháp. Hiện nay 
tác giả đang là giảng viên Khoa Kỹ thuật điện, Trường Đại học Điện lực. 
Lĩnh vực nghiên cứu: Mô hình hóa hệ thống điện từ, ứng dụng các phương pháp 
số (phương pháp phần tử hữu hạn và phương pháp tích phân hữu hạn) trong 
nghiên cứu máy điện và hệ thống điện, tác động của điện từ trường tương hỗ và 
tiết kiệm năng lượng trong thiết bị điện. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
24 Số 23 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 25