Một vài ứng dụng đạo hàm cấp phân số trong cơ điện tử

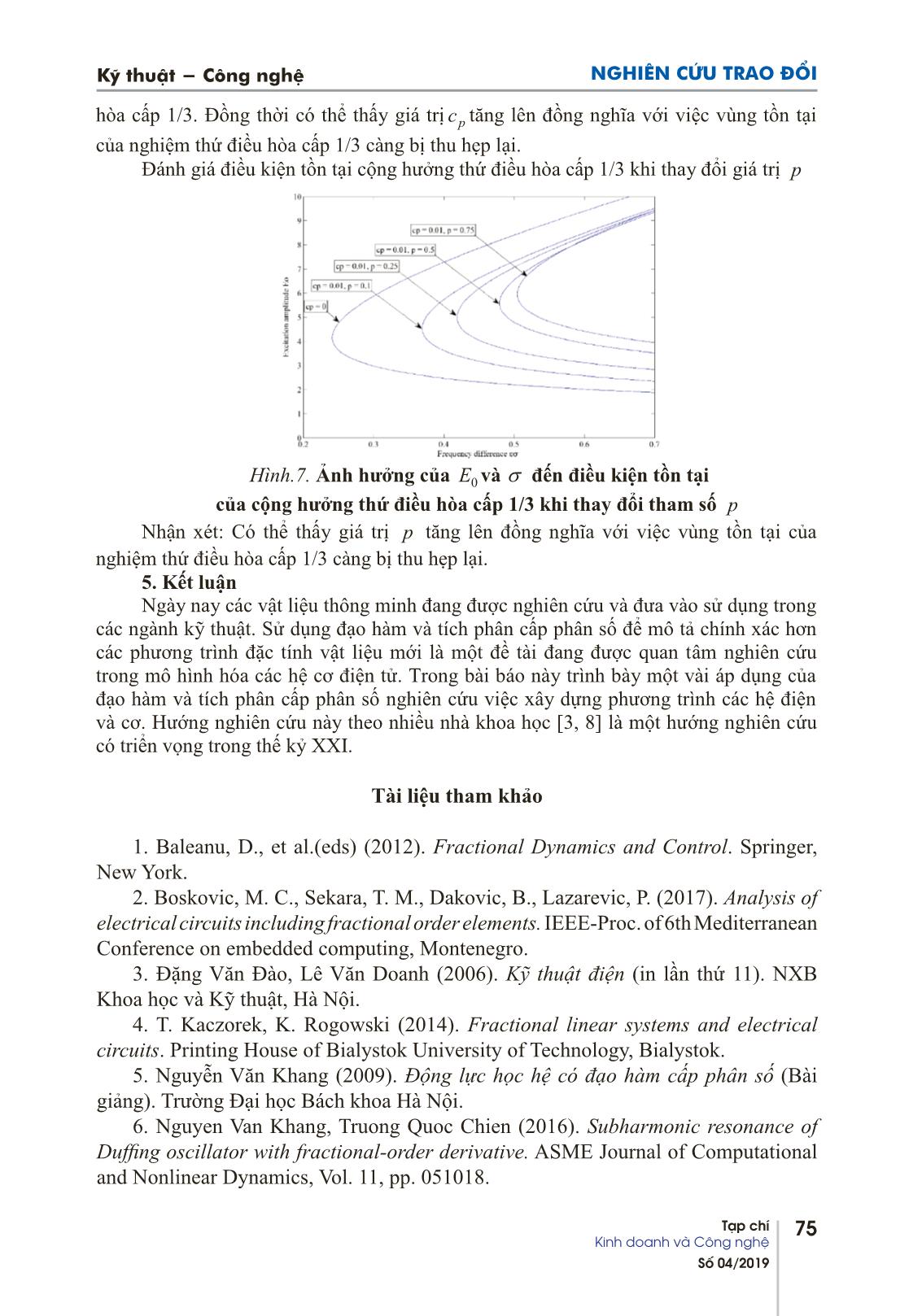
Kỹ thuật - Công nghệ NGHIÊN CỨU TRAO ĐỔI
67Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
MỘT VÀI ỨNG DỤNG ĐẠO HÀM CẤP PHÂN SỐ TRONG CƠ ĐIỆN TỬ
Some applications of fractional-order derivatives in Mechatronics
GS. TSKH. NGND. Nguyễn Văn Khang *
Tóm tắt: Đạo hàm và tích phân cấp phân số có vai trò quan trọng trong việc mô tả 
tính chất vật lý của các loại vật liệu mới xuất hiện ở cuối thế kỷ XX - đầu thế kỷ XXI. 
Bài viết giới thiệu một số định nghĩa về đạo hàm cấp phân số và trình bày việc áp dụng 
của đạo hàm cấp phân số trong mô hình các hệ cơ điện tử.
Từ khóa: Đạo hàm cấp phân số, cơ điện tử, dao động, mạch điện RLC.
Abstract: The fractional derivative and the integral play an important role in 
describing the physical properties of new materials created at the end of the 20th 
century and at the beginning of the 21st century. Some definitions of the broken 
derivative are presented in this work. Subsequently, some applications of fractional 
derivative are presented in the models of mechatronic systems.
Keywords: Fractional-order derivative, mechatronics, vibration, RLC circuit.
* Phó Chủ nhiệm khoa Cơ – Điện tử
 Trường ĐH KD&CN Hà Nội
1. Mở đầu 
Tr ong bức thư ngày 30 tháng 09 năm 1695 của nhà toán học Đức Leibniz (1646-
1716) gửi nhà toán học Pháp L’Hospital, lần đầu tiên khái niệm đạo hàm cấp không 
nguyên được đề cập đến [1]. Trả lời câu hỏi của L’Hospital: “Biểu thức đạo hàm 
n
n
d
dx
có ý nghĩa như thế nào khi 12n ”, Leibn z nói: “Sẽ dẫn đến một mâu thuẫn” và ông 
viết thêm: “Từ mâu thuẫn này đến một ngày nào đó sẽ có những kết luận hữu ích”. 
Cuối thế kỷ XIX, lý thuyết đạo hàm và tích phân cấp phân số đã được nghiên cứu 
bởi các nhà toán học Liouville, Grünwald, Letnikov, Riemann, v.v Cơ sở toán học 
của lý thuyết đạo hàm cấp phân số được trình bày trong các tài liệu [2], [3], [4]. 
Lúc đầu lý thuyết đạo hàm cấp phân số được phát triển chủ yếu như là một lĩnh 
vực lý thuyết thuần tuý của toán học và chỉ hữu ích cho các nhà toán học. Tuy nhiên, 
một vài chục năm gần đây, nhiều tác giả đã chỉ ra rằng đạo hàm và tích phân cấp không 
nguyên rất phù hợp cho sự mô tả tính chất của nhiều loại vật liệu mới, chẳng hạn như 
vật liệu polyme. Họ cũng chỉ ra rằng những mô hình cấp phân số thích hợp hơn những 
mô hình cấp nguyên đã được sử dụng trước đó. Sự xem xét về mặt vật lý càng cho thấy 
việc sử dụng các mô hình dựa trên đạo hàm cấp phân số là hợp lý và phù hợp [2, 3]. 
Đạo hàm cấp phân số cung cấp một công cụ mới để mô tả bộ nhớ và tính chất di 
truyền của những vật liệu và quá trình khác nhau. Đây là ưu điểm chính của đạo hàm 
cấp phân số so với những mô hình đạo hàm cấp nguyên cổ điển, trong đó những ảnh 
hưởng như vậy trong thực tế bị bỏ qua 
NGHIÊN CỨU TRAO ĐỔI Kỹ thuật - Công nghệ
68Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
Việc mô hình toán học và mô phỏng các hệ cơ và các hệ điện tử dựa trên sự mô tả 
những tính chất của chúng thông qua đạo hàm cấp phân số tất nhiên sẽ dẫn tới những 
phương trình vi phân cấp phân số và dẫn tới sự cần thiết phải giải những phương trình 
như vậy. Trong bài báo này đầu tiên trình bày một cách ngắn gọn các định nghĩa về đạo 
hàm và tích phân cấp phân số, sau đó trình bày một vài kết quả nghiên cứu áp dụng khái 
niệm đạo hàm cấp phân số trong một vài bài toán cơ điện tử. 
2. Định nghĩa đạo hàm và tích phân cấp phân số 
2.1. Định nghĩa đạo hàm và tích phân cấp phân số theo Riemann-Liouville 
Công thức tích phân Cauchy có dạng: 
11
, ( 0)
t
nn
a
a
D f t t f d n
n
  
 
 (1) 
Mở rộng khái niệm tích phân với giá trị không nguyên của n, thay thế số nguyên n 
bằng số thực 0 p trong công thức tích phân Cauchy (1) ta có: 
11
, ( 0) (2)
t
pR p
t
a
D f t t f d p
p
  
 
 (2) 
Biểu thức (2) được định nghĩa là tích phân cấp phân số theo Riemann-Liouville [2, 
3]. Khi 0 p [2, 3], người ta định nghĩa 
11
(3)
( )
0, 1
tn
n pR p
t n
a
d
D f t t f d
n p dt
p n p n
  
 
 (3) 
là đạo hàm cấp phân số theo Riemann-Liouville [2, 3]. Các định nghĩa đạo hàm và 
tích phân cấp phân số theo Riemann-Liouville có ứng dụng rất phổ biến trong các lĩnh 
vực của khoa học tự nhiên và khoa học kỹ thuật. 
2.2. Định nghĩa đạo hàm và tích phân cấp phân số theo Grünwald-Letnikov 
Dựa trên công thức viết cho đạo hàm và tích phân với n nguyên, Grünwald-
Letnikov đã đưa ra định nghĩa về đạo hàm và tích phân cấp phân số với p là số thực tùy 
ý [2, 3]: 
1
0
lim
1
pp
G p
t p N
N
j
d f t t a
D f t
Nd t a
j p t a
f t j
p j N
 
    

 (4) 
 Đại lượng 
 1
1
1 
  
  
j
j p j p
A
j j p
 (5) 
được gọi là hệ số Grünwald. 
Cách định nghĩa theo Grünwald-Letnikov như trên có ưu điểm là đạo hàm, tích 
phân cấp phân số được tìm thông qua giá trị của hàm, không cần các phép tính tích phân 
và đạo hàm của nó. Người ta đã chứng minh được rằng hàm 0 p p có thể 
Kỹ thuật - Công nghệ NGHIÊN CỨU TRAO ĐỔI
69Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
không hữu hạn nhưng tỉ số 
 
 
j p
p
 là hữu hạn. Sự tương đương của các định nghĩa đạo 
hàm cấp phân số đã được chứng minh trong các tài liệu [2, 3, 5]. 
 2.3. Định nghĩa đạo hàm cấp phân số theo Caputo 
 Đạo hàm cấp phân số định nghĩa theo Caputo có dạng: 
11
,
tn
n pC p
t n
a
d
D f t t f d
n p dt
  
 
 1n p n (6) 
 Giữa đạo hàm cấp phân số theo Riemann-Liouvill và theo Caputo người ta tìm 
được quan hệ [5]: 
( )1
0 1
jn
j pR p c p
a a
j
f a
D f t D f t t a
j p
 
 (7) 
 Nếu 0 0, , 1 jf a j n thì hai định nghĩa trên trùng nhau. 
 2.4. Định nghĩa đạo hàm và tích phân cấp phân số theo hàm biến phức 
 Cho f z là hàm đơn trị và giải tích trong miền mở A của mặt phẳng phức, A là 
tập các điểm trong của A bị chặn bởi đường cong đóng trơn C thì tích phân Cauchy có 
dạng [2, 3, 5]: 
1
,
2
C
f
f z d z A
i z


 
  
(8) 
Từ (8) ta có công thức tính đạo hàm cấp nguyên: 
1
!
2
n
n
C
fn
D f z d
i z


 
 (9) 
Hình 1. Chu tuyến L 
 Khi n là số p bất kỳ, thì ta có thể thay thế !n trong biểu thức (9) bằng hàm 
( 1)p .Tuy nhiên, nếu p không phải là một số nguyên thì điểm z sẽ trở thành điểm 
phân nhánh và không phải là cực của hàm dưới dấu tích phân trong biểu thức (9). Do 
đó, đường cong C không còn là một tuyến phù hợp. Để giải quyết vấn đề này ta dựng 
một nhát cắt dọc trục thực từ điểm z tới . Trong hình 1, giả sử z là một số thực 
dương, ký hiệu là x. Khi đó định nghĩa paD f z dưới dạng tích phân đường x a 
NGHIÊN CỨU TRAO ĐỔI Kỹ thuật - Công nghệ
70Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
1
1
1
2
1
2
x
pp
a
a
p
L
p
D f z x f d
i
p
x f d
i
  
  
 
 
 (10) 
 Từ biểu thức (10) người ta có thể biến đổi dẫn đến biểu thức định nghĩa tích 
phân cấp phân số theo Riemann-Liouville (2) [5]. 
3. Ứng dụng đạo hàm cấp phân số trong kỹ thuật điện 
Như chúng ta đã biết [6] khi dòng điện i(t) chạy qua cuộn dây theo định luật cảm 
biến điện từ, điện áp trong cuộn dây có dạng: 
( )
L
di t
u L
dt
 Khi điện áp trên tụ điện có điện dung C biến thiên thì dòng điện chuyển dịch qua 
tụ điện được xác định bởi công thức: 
( )Cdu ti C
dt
 Các công thức trên được xác định bằng thực nghiệm. Sử dụng khái niệm đạo 
hàm cấp phân số, các công thức cơ bản trên có dạng [7, 8]: 
( )
( ) , 0 1C
d u t
i t C
dt
( )
( ) , 0 1
d i t
u t L
dt


 
Thí dụ 1. Để minh họa, ta thiết lập phương trình trạng thái của mạch điện RLC 
nối tiếp như sau. 
Hình 2. Mạch RLC nối tiếp 
 Dòng điện được tính theo điện áp trên tụ điện: 
( )
( ) C
du t
i t C
dt
 Điện áp rơi trên điện trở và điện áp rơi trên điện cảm 
( )
( ) ( ) CR R
du t
u Ri t u Ri t RC
dt
2
2
( )( )
( ) CL
d u tdi t
u t L LC
dt dt
i 
u 
R 
C uC 
uR uL 
L 
Kỹ thuật - Công nghệ NGHIÊN CỨU TRAO ĐỔI
71Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
2
2
( ) ( ) ( ) ( )
( ) ( )
( )
L R C
C C
C
u t u t u t u t
d u t du t
LC RC u t
dtdt
hay: 
2
2
( ) ( )
( ) ( )C C C
d u t du t
LC RC u t u t
dtdt
 . (11) 
 Nếu sử dụng các công thức đạo hàm cấp phân số ta có: 
( ) ( )
( ) ( )C C C
d u t d u t
LC RC u t u t
dt dt
 
 
 (12) 
Trong đó 0 1, 1 2  . 
 Các kết quả tính toán theo phương trình (12) gần với các kết quả thực nghiệm 
hơn các kết quả tính toán theo phương trình (11) [7, 8]. 
4. Ứng dụng đạo hàm cấp phân số trong kỹ thuật dao động 
Trong những năm gần đây việc áp dụng đạo hàm cấp phân số trong tính toán dao 
động của các cơ hệ có các vật liệu mới, các vật liệu thông minh được quan tâm nghiên 
cứu nhiều [2 -5]. Ta nêu một vài điểm khác biệt như sau. 
Thứ nhất, quy luật cản không cò là cản bậc nhất hoặc cản bậc hai như các tài liệu 
cổ điển: 
x
C
dF a dt hoặc 
2
2
x
C
dF b
dt
 (13) 
mà là cản cấp phân số: 
x
C
dF c
dt
 (14) 
với là một số không nguyên hoặc một số phức. 
Thứ hai, quan hệ giữa ứng suất-biến dạng không còn tuân theo định luật Hook cổ 
điển: 
x xx xE  (15) 
mà có dạng 
x
x x( )
x
x x a
dE
dt

   (16) 
với là một số không nguyên hoặc một số phức. 
NGHIÊN CỨU TRAO ĐỔI Kỹ thuật - Công nghệ
72Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
Thí dụ 2. Thiết lập phương trình vi phân dao động của giá treo ô tô: 
Gọi x1, x2 và u là dịch chuyển của các vật và bánh xe. Ta có định luật 2 Newton 
1 1 1
2 2 1 2
,
,
m x R
m x R R
 (17) 
Trong đó 1 2,R R là nội lực sinh ra bên trong vật thể đàn nhớt. Giá trị lực 2R bằng 
tổng giá trị lực tác dụng lên giảm chấn 2c và lực tác dụng lên lò xo k 
 1 1 1 2 ,R c x x (18) 
 22 2 2
,k cR R R 
 (19) 
Trong đó : 
 22 2 22 2, ,tk cR k x u R c D x u
 (20) 
 2 2 2 2 ,tR c D x u k x u
 (21) 
 Từ phương trình (17), (18) và (21) ta có phương trình vi phân chuyển động của 
cơ hệ 
 1 1 1 1 2m x c x x (22) 
 2 2 1 1 2 2 2 2 ,tm x c x x c D x u k x u
 (23) 
Rút 1x từ phương trình (23) 
2 2
1 2 2 2 2
1 1 1
2
1 1
,
t
t
m c k
x x x D x x
c c c
c k
D u u
c c
 (24) 
Đạo hàm phương trình (24) ta được : 
Kỹ thuật - Công nghệ NGHIÊN CỨU TRAO ĐỔI
73Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
12 2
1 2 2 2 2
1 1 1
12
1 1
,
t
t
m c k
x x x D x x
c c c
c k
D u u
c c
 (25) 
Thay phương trình (24) và (25) vào (22) ta được phương trình vi phân cấp ba sau 
11 1 2
2 2 2 2
1 2 2 2
1 2 1
2 2
1 2 1 2
12 1 2 1
2 2 1 2 1 2
.
t
t
t t
c c c k
x x D x x
m m m m
c c kc
D x x
m m m m
c c c kck
D u u D u u
m m m m m m
(26) 
Thí dụ 3. Dao động phi tuyến có thành phần cản cấp phân số [9, 10]. 
Xét dao động của hệ Duffing như hình 5. 
Phương trình vi phân mô tả dao động có dạng
3
1 3
0 cos
p
pmx t k x t cx t k x t c D x t
E t
 
 (27) 
 Trong đó: 
 m : khối lượng cơ hệ ( kg ) ; 
 1k : hệ số độ cứng tuyến tính ( 2
kg
s
) ; 
c : hệ số cản nhớt tuyến tính (
kg
s
) ; 
3k : hệ số độ cứng phi tuyến ( 2 2
kg
cm s
) ; 
0E : biên độ lực cưỡng bức ( N ) ; 
  : tần số góc lực cưỡng bức (
rad
s
) ; 
 Hình 5. Mô hình Duffing 
NGHIÊN CỨU TRAO ĐỔI Kỹ thuật - Công nghệ
74Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
 p
c : hệ số của thành phần cấp phân số ( 2 p
kg
s 
) ; 
[ ( )]ppc D x t : thành phần đạo hàm cấp phân số 0; 0 1pc p . 
 Thực hiện phép đổi biến 
3 01
0 ;2 ; ; ;
p
p
ck Ek c E
m m m m m
    
 (28) 
Khi đó phương trình (27) trở thành : 
2 3
0 2
cospp
x t x t x t x t
D x t E t
   

  
 (29) 
Xét trường hợp khi tần số của ngoại lực cưỡng bức  và tần số dao động riêng 
0 có mối quan hệ: 
2 2 2
03   (29) 
Khi đó (29) trở thành: 
2
2
3
2
3
2 x +
3
cos t (30)
p
p
x t x t
x t x t D t x t
E

  

 
  
 
 
Trong [9] đã áp dụng phương pháp trung bình hóa tìm nghiệm phương trình 
(30). Một vài kết quả biểu thị ảnh hưởng của của số hạng cấp phân số được trình 
bày trên các hình (6) và (7). 
Hình 6. Ảnh hưởng của 0E và  đến điều kiện tồn tại 
của cộng hưởng thứ điều hòa cấp 1/3 khi thay đổi tham số pc 
Nhận xét: Dựa trên biểu đồ trên ta có thể quan sát sự thay đổi của giá trị theo 
biên độ lực kích động 0E để thỏa mãn điều kiện tồn tại của nghiệm cộng hưởng thứ điều 
Kỹ thuật - Công nghệ NGHIÊN CỨU TRAO ĐỔI
75Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
hòa cấp 1/3. Đồng thời có thể thấy giá trị pc tăng lên đồng nghĩa với việc vùng tồn tại 
của nghiệm thứ điều hòa cấp 1/3 càng bị thu hẹp lại. 
Đánh giá điều kiện tồn tại cộng hưởng thứ điều hòa cấp 1/3 khi thay đổi giá trị p 
Hình.7. Ảnh hưởng của 0E và  đến điều kiện tồn tại 
của cộng hưởng thứ điều hòa cấp 1/3 khi thay đổi tham số p 
Nhận xét: Có thể thấy giá trị p tăng lên đồng nghĩa với việc vùng tồn tại của 
nghiệm thứ điều hòa cấp 1/3 càng bị thu hẹp lại. 
5. Kết luận 
Ngày nay các vật liệu thông minh đang được nghiên cứu và đưa vào sử dụng trong 
các ngành kỹ thuật. Sử dụng đạo hàm và tích phân cấp phân số để mô tả chính xác hơn 
các phương trình đặc tính vật liệu mới là một đề tài đang được quan tâm nghiên cứu 
trong mô hình hóa các hệ cơ điện tử. Trong bài báo này trình bày một vài áp dụng của 
đạo hàm và tích phân cấp phân số nghiên cứu việc xây dựng phương trình các hệ điện 
và cơ. Hướng nghiên cứu này theo nhiều nhà khoa học [3, 8] là một hướng nghiên cứu 
có triển vọng trong thế kỷ XXI. 
 Tài liệu tham khảo
1. Baleanu, D., et al.(eds) (2012). Fractional Dynamics and Control. Springer, 
New York.
2. Boskovic, M. C., Sekara, T. M., Dakovic, B., Lazarevic, P. (2017). Analysis of 
electrical circuits including fractional order elements. IEEE-Proc. of 6th Mediterranean 
Conference on embedded computing, Montenegro.
3. Đặng Văn Đào, Lê Văn Doanh (2006). Kỹ thuật điện (in lần thứ 11). NXB 
Khoa học và Kỹ thuật, Hà Nội.
4. T. Kaczorek, K. Rogowski (2014). Fractional linear systems and electrical 
circuits. Printing House of Bialystok University of Technology, Bialystok. 
5. Nguyễn Văn Khang (2009). Động lực học hệ có đạo hàm cấp phân số (Bài 
giảng). Trường Đại học Bách khoa Hà Nội.
6. Nguyen Van Khang, Truong Quoc Chien (2016). Subharmonic resonance of 
Duffing oscillator with fractional-order derivative. ASME Journal of Computational 
and Nonlinear Dynamics, Vol. 11, pp. 051018.
NGHIÊN CỨU TRAO ĐỔI Kỹ thuật - Công nghệ
76Tạp chí 
Kinh doanh và Công nghệ
Số 04/2019
7. Nguyen Van Khang, Bui Thi Thuy, Truong Quoc Chien (2016). Resonance 
oscillation of third order forced van der Pol system with fractional order derivative. 
ASME Journal of Computational and Nonlinear Dynamics, Vol.11, Issue 4, pp. 
0410301-0410305.
8. Leibniz, G. W. (1962). Mathematische Schiften. Georg Ohns Verlagsbuchhandlung, 
Hildesheim.
9. Miller, K. S. and Ross, B. (1993). An introduction to the Fractional Calculus 
and Fractional Differential Equations. John Wiley & Sons Inc., New York.
10. Bùi Thị Thúy (2017). Dao động phi tuyến yếu của hệ cấp ba có đạo hàm cấp 
phân số. Luận án Tiến sĩ, Học viện Khoa học và Công nghệ, Viện hàn lâm Khoa học 
và Công nghệ Việt Nam.
Ngày nhận bài: 05/7/2019