Một phương pháp điều khiển trượt mới không có pha tiếp cận

 và có thể gỡ bỏ hoàn toàn các nhiễu loạn. 
Tuy nhiên, các đặc điểm này chỉ có giá trị trong pha trượt [2],[3]. Thiết kế bề mặt 
trượt có thể cải thiện hiệu năng của bộ điều khiển bằng cách giảm thiểu hoặc loại 
bỏ thời gian tiếp cận để đạt đến pha trượt. Trong bài báo này, một phương pháp 
thiết kế bề mặt trượt mới được đề xuất nhằm đạt được mục đích nêu trên. 
Từ khóa: Pha trượt; Điều khiển trượt; Thiết kế bề mặt trượt mới. 
1. ĐẶT VẤN ĐỀ 
Quỹ đạo không gian trạng thái của hệ thống điều khiển chế độ trượt (Sliding mode 
control-SMC) có thể được chia thành hai phần thể hiện cho hai chế độ khác nhau của hoạt 
động hệ thống. Các quỹ đạo bắt đầu từ một điều kiện ban đầu ở xa bề mặt trượt và hướng 
về phía bề mặt trượt trong một khoảng thời gian xác định. Phần của quỹ đạo trước khi tiếp 
cận với bề mặt trượt được gọi là pha tiếp cận (reaching phase) và khoảng thời gian diễn ra 
của nó được gọi là thời gian tiếp cận (reaching time) [2], [3]. 
Hình 1. Điều khiển chế độ trượt. 
Khi quỹ đạo hội tụ đến bề mặt trượt, pha trượt (sliding phase) bắt đầu và quỹ đạo hệ 
thống nhanh chóng tiến về gốc tọa độ dọc theo bề mặt trượt trong một khoảng thời gian 
xác định được gọi là thời gian trượt (sliding time). Nói chung, thiết kế của một bộ điều 
khiển chế độ trượt (SMC) liên quan đến việc thiết kế một bề mặt trượt thể hiện động lực 
ổn định mong muốn và một luật điều khiển đảm bảo pha tiếp cận và pha trượt [8]. Trong 
pha tiếp cận các quỹ đạo hệ thống rất nhạy cảm với các biến đổi của tham số và nhiễu loạn 
nhưng trong pha trượt hệ thống bất biến với điều đó. Bài báo này đề xuất một mặt trượt 
mới đảm bảo triệt tiêu ảnh hưởng của pha tiếp cận đến chất lượng hoạt động của hệ thống 
và đảm bảo tính ổn định bền vững ngay từ điểm khởi đầu của hệ thống trong không gian 
trạng thái. 
2. MÔ TẢ HỆ THỐNG ĐIỀU KHIỂN PHI TUYẾN BẬC HAI 
Xét một lớp hệ thống điều khiển phi tuyến bậc hai được mô tả như sau: 
1 2
2 ( , ) ( , ) ( , ) ( )
x x
x f x t f x t b x t u d t


 (1) 
Kỹ thuật điều khiển & Điện tử 
C. T. Huỳnh, L. T. Thắng, T. V. Nhân, “Một phương pháp điều khiển trượt  pha tiếp cận.” 64 
Trong đó, 1 2,x x là các biến trạng thái của hệ thống và: 
 1 2( ) [ ( ) ( )]
Tx t x t x t (2) 
Là véc tơ trạng thái, t là thời gian, u là tín hiệu điều khiển; ,b f là các hàm số bị 
chặn đã biết; f là thành phần bất định của mô hình; d là các nhiễu loạn bên ngoài. Giả 
sử tồn tại một hằng số dương  là giá trị biên nhỏ nhất của giá trị tuyệt đối ( , )b x t : 
 inf{ ( , ) }= >0b x t  (3) 
Do f và d chưa biết và bị chặn nên tồn tại hằng số dương  sao cho: 
 ( , ) ( )f x t d t  (4) 
Các điều kiện ban đầu của hệ thống: 
 10 1 0 20 2 0( ); ( )x x t x x t (5) 
Quỹ đạo mong muốn của hệ thống (1) là một hàm số của thời gian: 
 1 2( ) [ ( ) ( )]
T
d d dx t x t x t (6) 
Trong đó, 2 1( ) ( )d dx t x t  là một hàm số vi phân theo thời gian. Sai số bám sát theo 
quỹ đạo được định nghĩa bởi véc tơ sau: 
 1 2( ) [ ( ) ( )] ( ) ( )
T
de t e t e t x t x t (7) 
Vậy: 
 1 1 1
( ) ( ) ( )de t x t x t (8) 
 2 2 2
( ) ( ) ( )de t x t x t (9) 
 1 0 0 0
( ) 0; 0;e t e t (10) 
Tọa độ điểm khởi đầu của hệ thống trong không gian sai số là 1 0 2 0( ( ), ( ))e t e t . Tọa độ 
này luôn xác định và phụ thuộc vào cấu trúc vật lý của hệ thống. 
3. THIẾT KẾ MẶT TRƯỢT MỚI 
3.1. Phân tích các đặc điểm của mặt trượt truyền thống 
Mặt trượt truyền thống cho hệ thống điều khiển phi tuyến bậc hai (1) có dạng như sau [2]: 
 2 1( , ) ( ) ( ) 0s e t e t ce t (11) 
Trong đó, 0c là một hằng số. 
Để xác định giá trị sai số bám sát 1( )e t và sai số theo tốc độ 2( )e t , cần giải phương 
trình: 
 2 1( ) ( ) 0e t ce t (12) 
Do 2 1( ) ( )e t e t  nên (12) được đưa về dạng phương trình vi phân bậc nhất của 1
( )e t : 
 1 1( ) ( ) 0e t ce t  (13) 
Với điều kiện ban đầu (10) và 0 0t , sử dụng phương pháp giải phương trình vi phân 
thông thường dễ dàng xác định được các nghiệm phương trình (13) trong khoảng thời gian: 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 65, 02 - 2020 65
1 0( )
cte t e e (14) 
2 0( )
cte t ce e (15) 
Từ (14) và (15) rút ra các nhận xét về mặt trượt truyền thống như sau [2] (hình 2): 
- Sai số bám sát của hệ thống hội tụ nhanh về 0 theo hàm mũ và không tồn tại bất kỳ độ 
quá chỉnh nào. 
- Nếu hệ số c nhỏ thì thời gian tiếp cận của hệ thống nhỏ, nhưng động học của hệ 
thống chậm. 
- Ngược lại, nếu hệ số c lớn thì thời gian tiếp cận của hệ thống lớn, nhưng động học 
của hệ thống lại nhanh hơn, hệ thống nhanh hội tụ hơn. 
Hình 2. Các đáp ứng sai số trong không gian trạng thái 
với các giá trị c khác nhau. 
Quá trình phân tích trong trong các phần trên đã chỉ rõ rằng việc lựa chọn mặt trượt sẽ 
quyết định đến hoạt động và hiệu năng của hệ thống (1). Mục tiêu của mặt trượt được đề 
xuất trong bài báo này là vừa đảm bảo được đặc tính động học nhanh của hệ thống, vừa loại 
bỏ được pha tiếp cận, đảm bảo tính ổn định bền vững của hệ thống ngay từ điểm khởi đầu. 
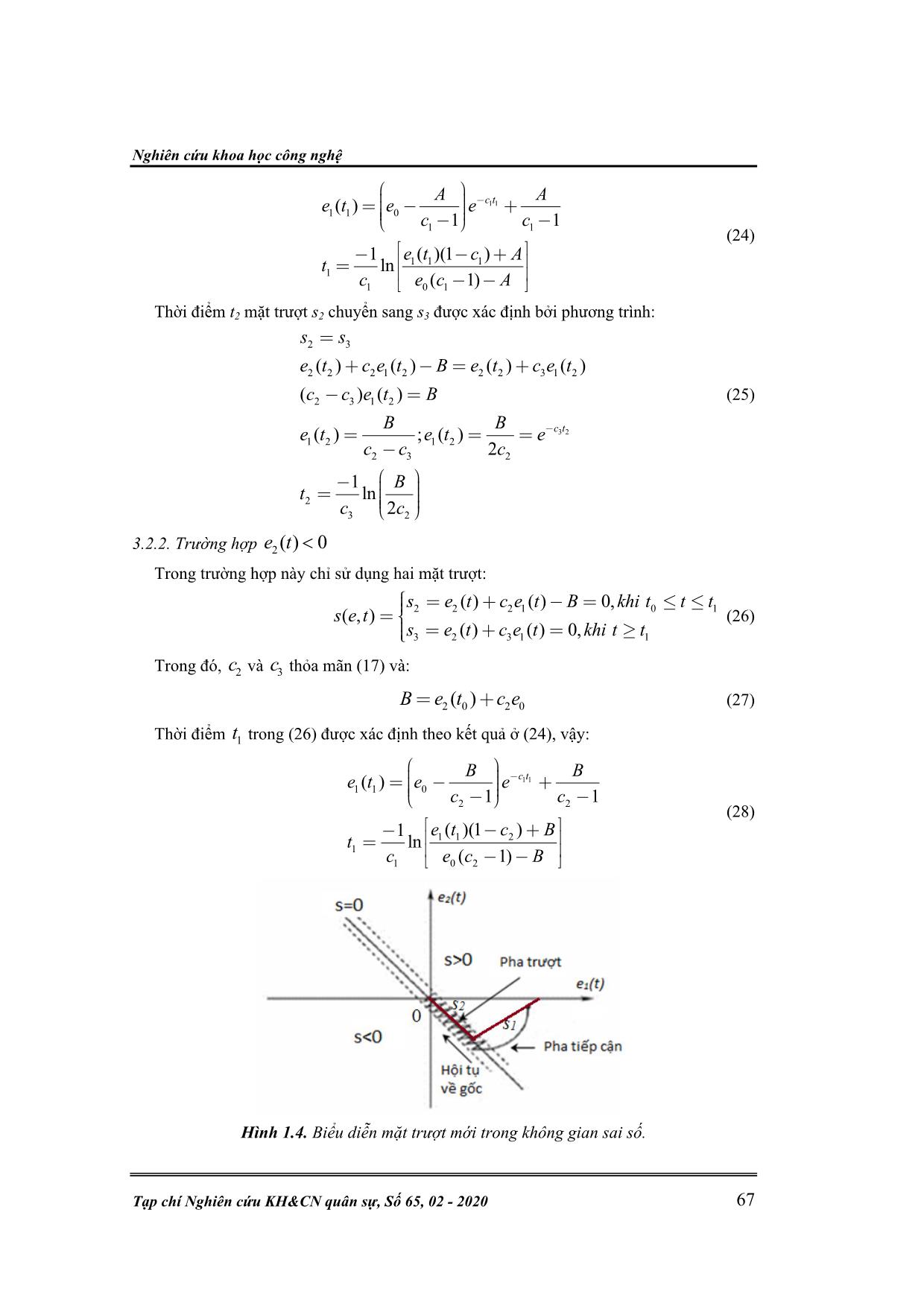
3.2. Đề xuất mặt trượt biến đổi mới 
Ý tưởng để loại bỏ pha tiếp cận đó là điểm đại diện ban đầu phải nằm trên mặt trượt 
ngay tại thời điểm ban đầu 0 0t .Vì thế, từ mặt trượt truyền thống (11), một mặt trượt 
mới được đề xuất như sau (hình 3): 
3.2.1. Trường hợp 2 ( ) 0e t 
1 2 1 1 1
2 2 2 1 1 2
3 2 3 1 2
( ) ( ) 0, 0
( , ) ( ) ( ) 0, 
( ) ( ) 0, 
s e t c e t A khi t t
s e t s e t c e t B khi t t t
s e t c e t khi t t
 (16) 
Trong đó: ,A B là các hằng số; mặt trượt 1s là một đường thẳng đi qua điểm ban đầu 
và song song với mặt trượt truyền thống 3s nên 1 3c c . Mặt trượt 2s và 1s sử dụng trục 
1( )e t làm đường phân giác nên hệ số góc của 1s là: 
 2 1 3
c c c (17) 
Kỹ thuật điều khiển & Điện tử 
C. T. Huỳnh, L. T. Thắng, T. V. Nhân, “Một phương pháp điều khiển trượt  pha tiếp cận.” 66 
Hình 3. Biễu diễn mặt trượt mới trong không gian sai số. 
Hơn nữa, để thực sự loại bỏ pha tiếp cận và đảm bảo tính bất biến với nhiễu loạn ngay 
từ khi bắt đầu sự chuyển động của nó thì các hằng số 1,c A phải được chọn như là điểm 
đại diện của hệ thống tại thời điểm ban đầu 0t t , nghĩa là mặt trượt 1s phải đi qua điểm 
ban đầu 2 0 1 0( ( ), ( ))e t e t 
Vì thế điều kiện sau phải được thỏa mãn: 
 1 2 0 1 1 0( ) ( ) 0s e t c e t A (18) 
Với điều kiện ban đầu (10) và 0 0t , sử dụng phương pháp giải phương trình vi phân 
thông thường dễ dàng xác định được các nghiệm phương trình (18) trong khoảng thời gian 
0 1,t t t   : 
1
1 0
1 1
( ) c t
A A
e t e e
c c
 (19) 
1
2 1 0
1
( ) c t
A
e t c e e
c
 (20) 
Từ (18) và 0 0t xác định được: 
 2 0 1 0
( )A e t c e (21) 
Để tính toán thời điểm chuyển sang sử dụng mặt trượt s2 cần giải phương trình: 
 1 1 1 1 1 1 1( ) ( ) ( )e t c e t A e t  (22) 
Trong đó, 1t là thời điểm mặt trượt s1 với trục e1(t). Từ đây tính được: 
 1 11 1 0
1 1
( )
1 1
c tA Ae t e e
c c
 (23) 
Vậy: 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 65, 02 - 2020 67
1 1
1 1 0
1 1
1 1 1
1
1 0 1
( )
1 1
( )(1 )1
ln
( 1)
c tA Ae t e e
c c
e t c A
t
c e c A
 (24) 
Thời điểm t2 mặt trượt s2 chuyển sang s3 được xác định bởi phương trình: 
3 2
2 3
2 2 2 1 2 2 2 3 1 2
2 3 1 2
1 2 1 2
2 3 2
2
3 2
( ) ( ) ( ) ( )
( ) ( )
( ) ; ( )
2
1
ln
2
c t
s s
e t c e t B e t c e t
c c e t B
B B
e t e t e
c c c
B
t
c c
 (25) 
3.2.2. Trường hợp 2 ( ) 0e t 
Trong trường hợp này chỉ sử dụng hai mặt trượt: 
2 2 2 1 0 1
3 2 3 1 1
( ) ( ) 0, 
( , )
( ) ( ) 0, 
s e t c e t B khi t t t
s e t
s e t c e t khi t t
 (26) 
Trong đó, 2c và 3c thỏa mãn (17) và: 
 2 0 2 0( )B e t c e (27) 
Thời điểm 1t trong (26) được xác định theo kết quả ở (24), vậy: 
1 1
1 1 0
2 2
1 1 2
1
1 0 2
( )
1 1
( )(1 )1
ln
( 1)
c tB Be t e e
c c
e t c B
t
c e c B
 (28) 
Hình 1.4. Biểu diễn mặt trượt mới trong không gian sai số. 
Kỹ thuật điều khiển & Điện tử 
C. T. Huỳnh, L. T. Thắng, T. V. Nhân, “Một phương pháp điều khiển trượt  pha tiếp cận.” 68 
4. XÂY DỰNG LUẬT ĐIỀU KHIỂN VỚI MẶT TRƯỢT ĐỀ XUẤT 
Xây dựng luật điều khiển với mặt trượt s1 
Chọn hàm Lyapunov dạng: 
2
1
1
2
V s . Đạo hàm của V là: 
1 1
V s s   . 
Đặt 1 1( )e e t , ta có: 
 1 1 1 1 1 1 1 1 1( ) [( ) ]dV s e c e s x x c e 
      (29) 
Do 
1 2
x x   , kết hợp (1) và (29) được: 
 1 1 1 1[ ]dV s x c e f f bu d 
   (30) 
Từ (30) đề xuất một luật điều khiển như sau: 
 1 1 1 1 1
1
[ sgn( ) ]du ks s x c e f
b
   (31) 
Trong đó: 0; 0.k 
Vậy: 
1 1 1
2
1 11
2
1 1 1
[ sgn( ) ]
( )
V s ks s f d
V ks s s f d
V ks s s f d






 (32) 
Kết hợp (4) ta được: 
2
1 1 1
2
1 1 ( )
V ks s s
V ks s
 
 


 (33) 
Vậy chỉ cần chọn   sẽ đảm bảo cho 0V  . Mặt khác, từ (33) dễ thấy: 0V  với 
mọi giá trị 
1
0s . Theo lý thuyết hàm Lyapunov hệ thống (1) ổn định tiệm cận (đpcm). 
Do các mặt trượt trong (16) và (26) có dạng giống nhau nên bộ điều khiển dạng (31) 
cũng đảm bảo cho hệ thống (1) ổn định tiệm cận trong các trường hợp sử dụng mặt trượt 
khác nhau trong hai trường hợp đã phân tích trong các mục (3.2.1) và (3.2.2). 
5. KẾT QUẢ MÔ PHỎNG 
Mô phỏng HTĐBSMT sử dụng động cơ một chiều không chổi than (Torque BLDC 
motor) có mô hình toán học đầy đủ được mô tả như sau [9]: 
[ ( ) ( ) ( )] ( ) ( ) ( )K T T x t T x t x t f x d t u te e m m    (34) 
Trong đó, Te là hằng số điện từ, Tm là hằng số điện cơ, Ke là hệ số tỷ lệ. 
Vậy: a3=KeTeTm; a2=KeTm; a1=Ke; 
Thực hiện mô phỏng với động cơ điện S Series Brushless Torque Motor- Aerotech S-
180-44-A có công suất 313W, các tham số được quy đổi theo [5],[6]. Tham số momen 
quán tính của hệ thống được tính trên cơ sở tải cân bằng và có khối lượng 30 kg. Các tham 
số của đối tượng: 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 65, 02 - 2020 69
1 2 3
31
3
2, 2 / ; 7, 40 10 ; 3, 4 10
12,8 ; 2,5650897; 17 10 ( ); 0, 27 10 ( )
4,3606525; 1,177376 10
K Nm A J kgm L Ht
R K T s T L R se m e
K T K T Te m e e m
  
Các hệ số ai : 
3
1 2 3
2,5650897; 4,3606525; 1,177376 10a a a
Vậy 1 2
2,5650897; 4,3606525
n n
a a 
. 
Do a3 quá nhỏ nên có thể bỏ qua số hạng chứa a3 trong (34) mà hầu như không ảnh 
hưởng nhiều đến chất lượng động học của hệ thống [7]. 
Lúc này phương trình dùng mô phỏng có dạng: 
[ ( ) ( )] ( ) ( ) ( )K T x t x t f x d t u te m   (35) 
Đưa (35) về dạng (1) và áp dụng các kết quả đã nghiên cứu để mô phỏng. 
Đặt : [ ( ) ] 105 2d t sin t sin t  , vậy trong (33) chọn 10 , do 
0k tùy ý nên có thể chọn 15k . Tín hiệu đặt: ).(dx t sin t 
Hình 5. Sơ đồ mô phỏng. 
Hình 6. Quỹ đạo pha của hệ thống luôn ở pha trượt khi chọn thời điểm 
chuyển mặt trượt đúng (đối với mặt trượt đề xuất (16)). 
Kỹ thuật điều khiển & Điện tử 
C. T. Huỳnh, L. T. Thắng, T. V. Nhân, “Một phương pháp điều khiển trượt  pha tiếp cận.” 70 
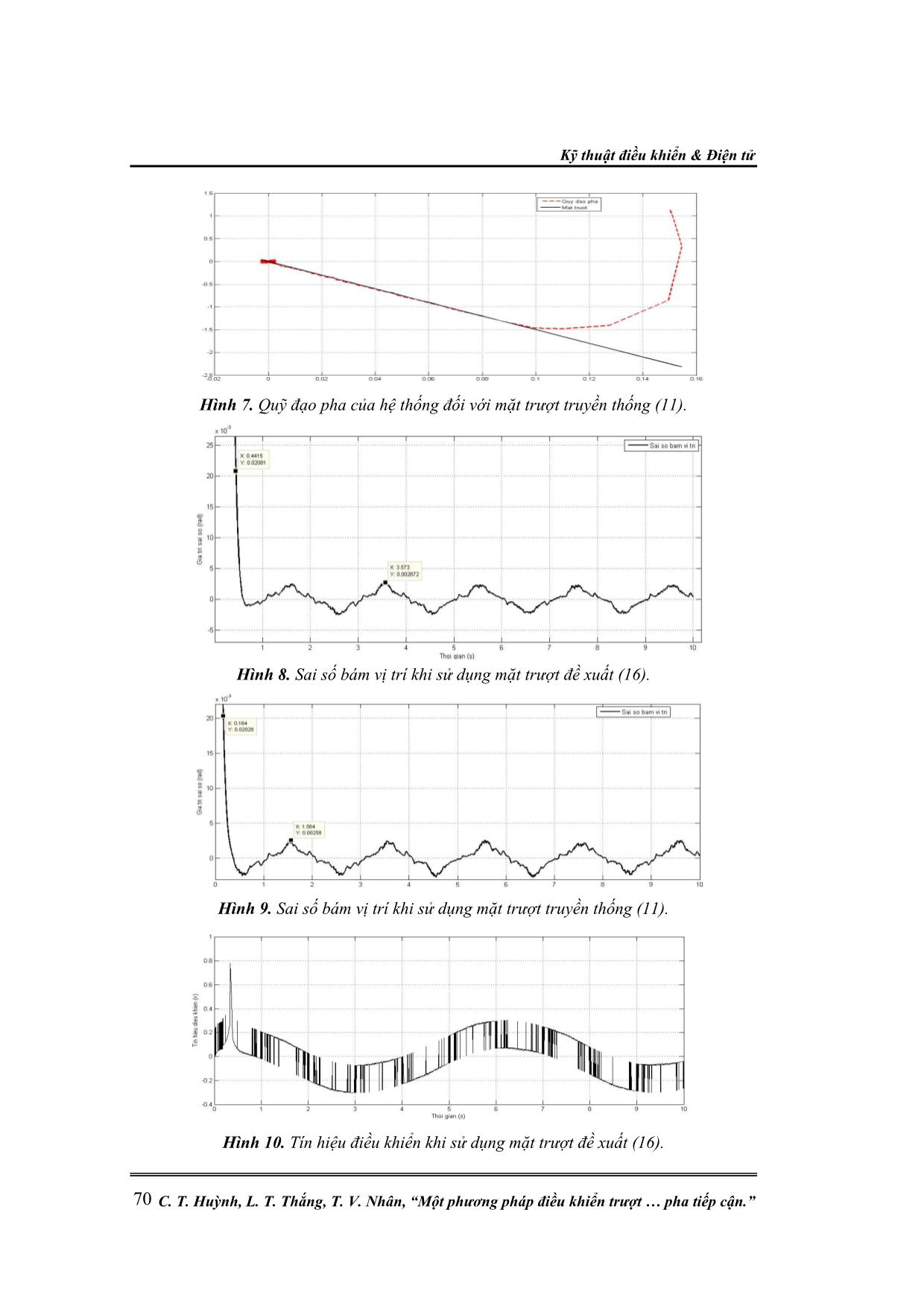
Hình 7. Quỹ đạo pha của hệ thống đối với mặt trượt truyền thống (11). 
Hình 8. Sai số bám vị trí khi sử dụng mặt trượt đề xuất (16). 
Hình 9. Sai số bám vị trí khi sử dụng mặt trượt truyền thống (11). 
Hình 10. Tín hiệu điều khiển khi sử dụng mặt trượt đề xuất (16). 
Nghiên cứu khoa học công nghệ 
Tạp chí Nghiên cứu KH&CN quân sự, Số 65, 02 - 2020 71
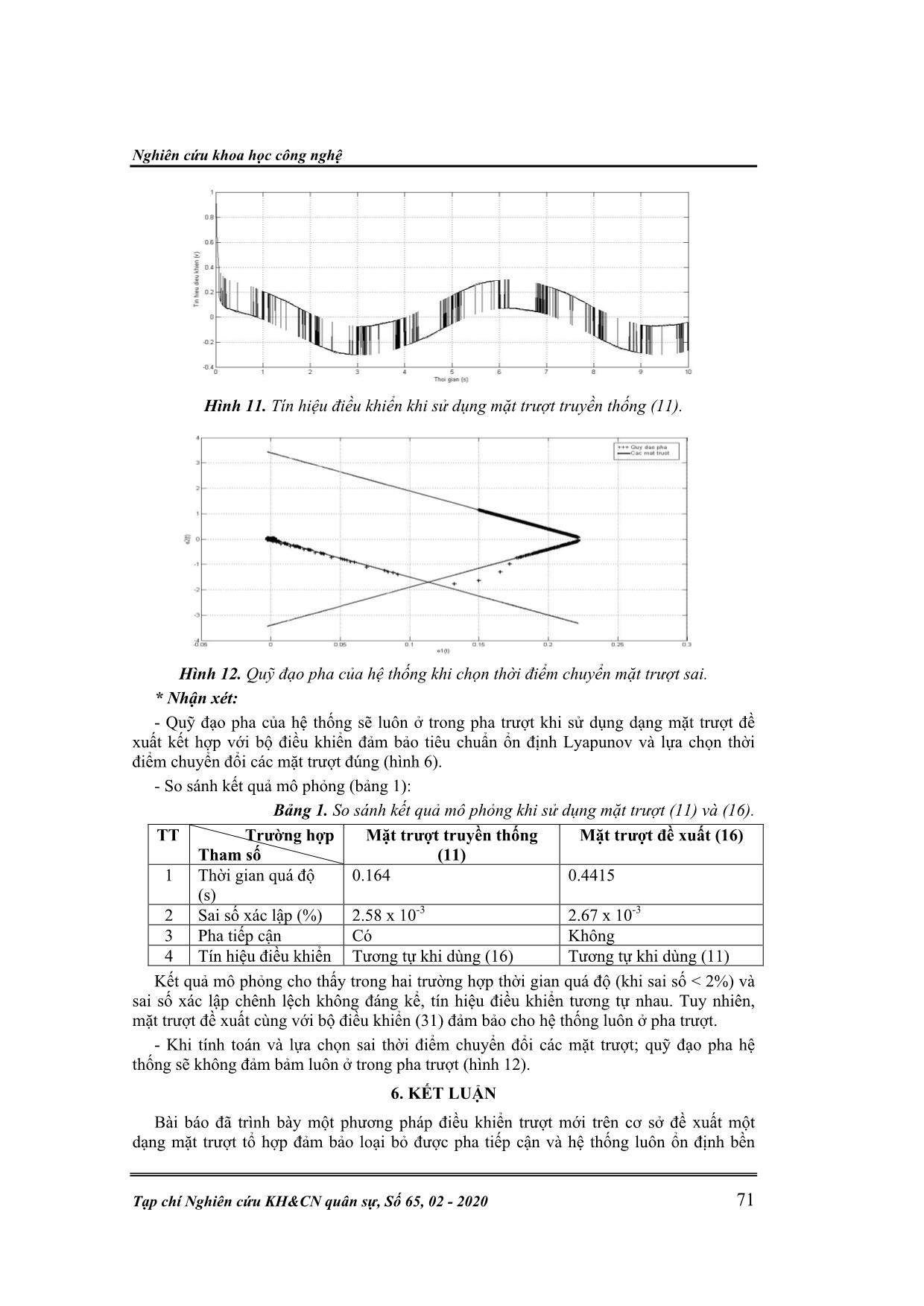
Hình 11. Tín hiệu điều khiển khi sử dụng mặt trượt truyền thống (11). 
Hình 12. Quỹ đạo pha của hệ thống khi chọn thời điểm chuyển mặt trượt sai. 
 * Nhận xét: 
- Quỹ đạo pha của hệ thống sẽ luôn ở trong pha trượt khi sử dụng dạng mặt trượt đề 
xuất kết hợp với bộ điều khiển đảm bảo tiêu chuẩn ổn định Lyapunov và lựa chọn thời 
điểm chuyển đổi các mặt trượt đúng (hình 6). 
- So sánh kết quả mô phỏng (bảng 1): 
Bảng 1. So sánh kết quả mô phỏng khi sử dụng mặt trượt (11) và (16). 
TT Trường hợp 
Tham số 
Mặt trượt truyền thống 
(11) 
Mặt trượt đề xuất (16) 
1 Thời gian quá độ 
(s) 
0.164 0.4415 
2 Sai số xác lập (%) 2.58 x 10-3 2.67 x 10-3 
3 Pha tiếp cận Có Không 
4 Tín hiệu điều khiển Tương tự khi dùng (16) Tương tự khi dùng (11) 
Kết quả mô phỏng cho thấy trong hai trường hợp thời gian quá độ (khi sai số < 2%) và 
sai số xác lập chênh lệch không đáng kể, tín hiệu điều khiển tương tự nhau. Tuy nhiên, 
mặt trượt đề xuất cùng với bộ điều khiển (31) đảm bảo cho hệ thống luôn ở pha trượt. 
- Khi tính toán và lựa chọn sai thời điểm chuyển đổi các mặt trượt; quỹ đạo pha hệ 
thống sẽ không đảm bảm luôn ở trong pha trượt (hình 12). 
6. KẾT LUẬN 
Bài báo đã trình bày một phương pháp điều khiển trượt mới trên cơ sở đề xuất một 
dạng mặt trượt tổ hợp đảm bảo loại bỏ được pha tiếp cận và hệ thống luôn ổn định bền 
Kỹ thuật điều khiển & Điện tử 
C. T. Huỳnh, L. T. Thắng, T. V. Nhân, “Một phương pháp điều khiển trượt  pha tiếp cận.” 72 
vững ngay từ điểm khởi đầu của hệ thống. Các kết quả chứng minh bằng lý thuyết và mô 
phỏng của bài báo làm tăng thêm tính ưu việt cho điều khiển trượt. 
TÀI LIỆU THAM KHẢO 
[1]. Editors: Xinghuo Yu · Mehmet Önder Efe, “Recent Advances in Sliding Modes: From 
Control to Intelligent Mechatronics”, Springer International Publishing Switzerland, 
2015. 
[2]. Vadim Utkin, Jurgen Guldner, Jingxin Shi, “Advanced Sliding Mode Control for 
Electromechanical Systems”, (Second Edition), Taylor & Francis Inc, America, 2009. 
[3]. Vadim Utkin, “ Sliding Modes in Control and Optimization”, Springer, Berlin, 1992. 
[4]. Andrei A. Agrachev, A. Stephen Morse, Eduardo D. Sontag, Héctor J. Sussmann, 
Vadim I. Utkin, “Nonlinear and Optimal Control Theory: Lectures given at the 
C.I.M.E. Summer School held in Cetraro”, Italy, June 19–29, 2004. 
[5]. PITTMAN Motors, Servo motor application note. 
[6]. Aerotech.Inc,
series.aspx?p=%2fproduct-catalog%2fmotors.aspx 
[7]. Смольников П.П., Синтез квазиоптимальных систем автоматического 
управления. Энергия, Ленинград 1987. 
[8]. Asif Chalanga, MachhindranathPatil, BijnanBandyopadhyay, Hemendra Arya, 
“Output regulation using new sliding surface with an implementation on inverted 
pendulum system”, European Journal of Control 45, tr 85–91, 2019. 
[9]. Nguyễn Trung Kiên, “Xây dựng phương pháp tổng hợp hệ thống điều khiển các đài 
quan sát tự động định vị từ xa các đối tượng di động”, Luận án tiến sỹ kỹ thuật, Viện 
Khoa học và Công nghệ quân sự, 2015. 
ABSTRACT 
A NEW SLIDING CONTROL METHOD 
WITHOUT THE REACHING PHASE 
Sliding mode control provides insensitivity to parameter variations and complete 
rejection of disturbances. However, this property is only valid in the sliding phase. 
Sliding surface design can be used to improve controller performance by 
minimizing or eliminating the time to reach the sliding phase. In this paper, a new 
sliding surface design method is proposed to achieve the above purpose. 
Keywords: Sliding phase; Sliding mode control; New sliding surface design. 
Nhận bài ngày 15 tháng 11 năm 2019 
Hoàn thiện ngày 15 tháng 01 năm 2020 
Chấp nhận đăng ngày 17 tháng 02 năm 2020 
Địa chỉ: 1 Viện Tự động hóa Kỹ thuật quân sự; 
 2 Học viện Hải quân. 
 *Email: tranvannhannt@gmail.com.