Inversion of multiple data sets acquired by different array configuration of geoelectrical resistivity method

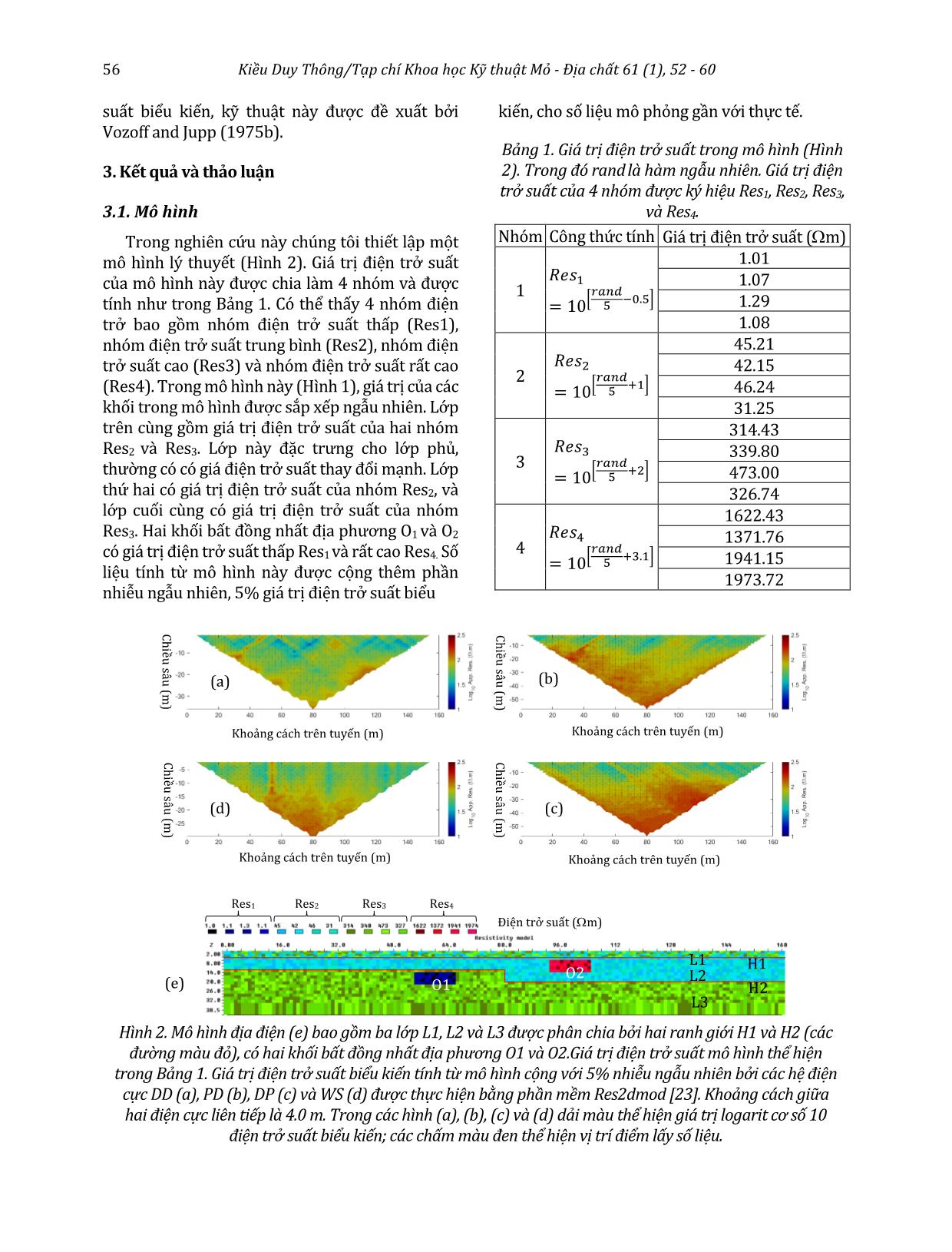
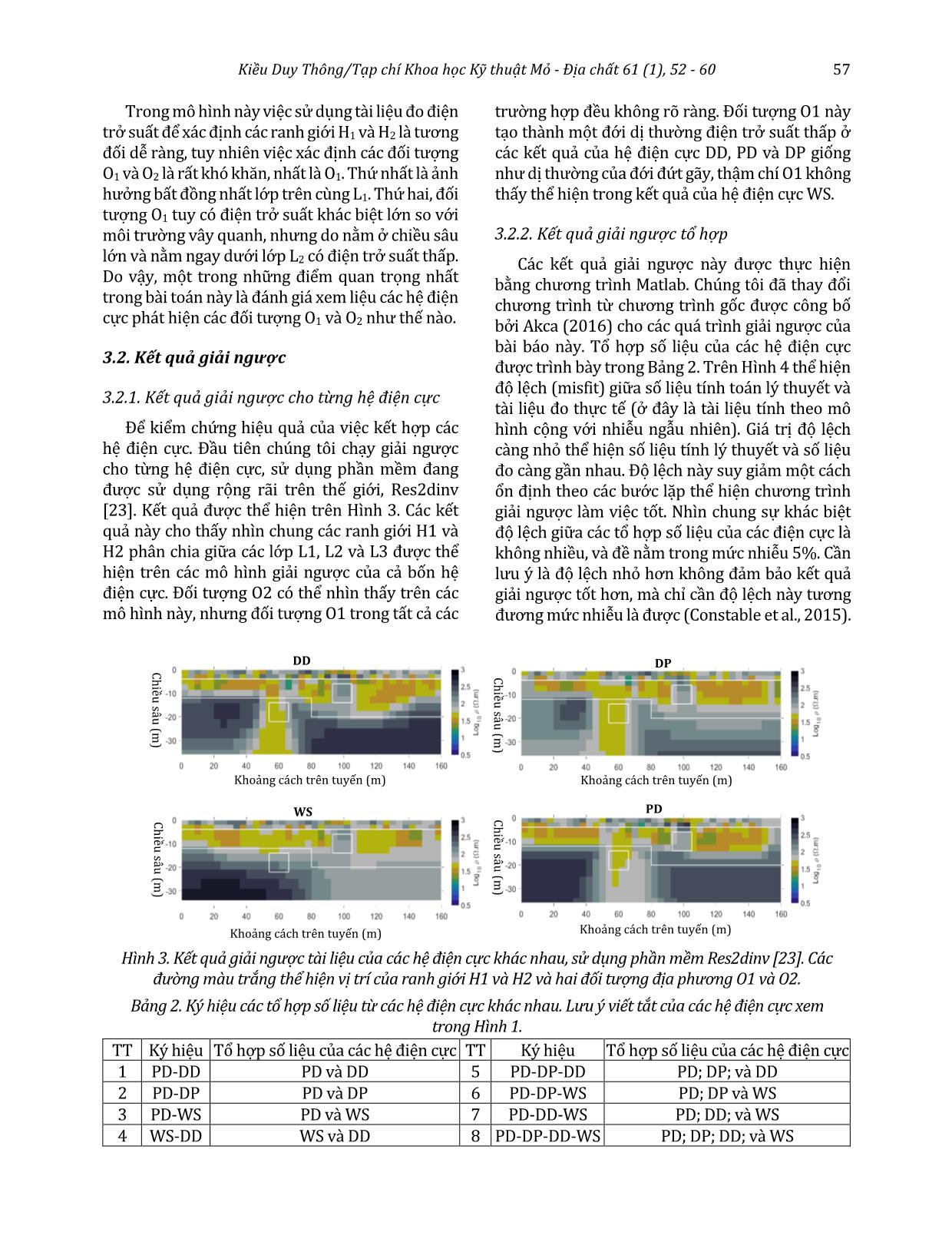
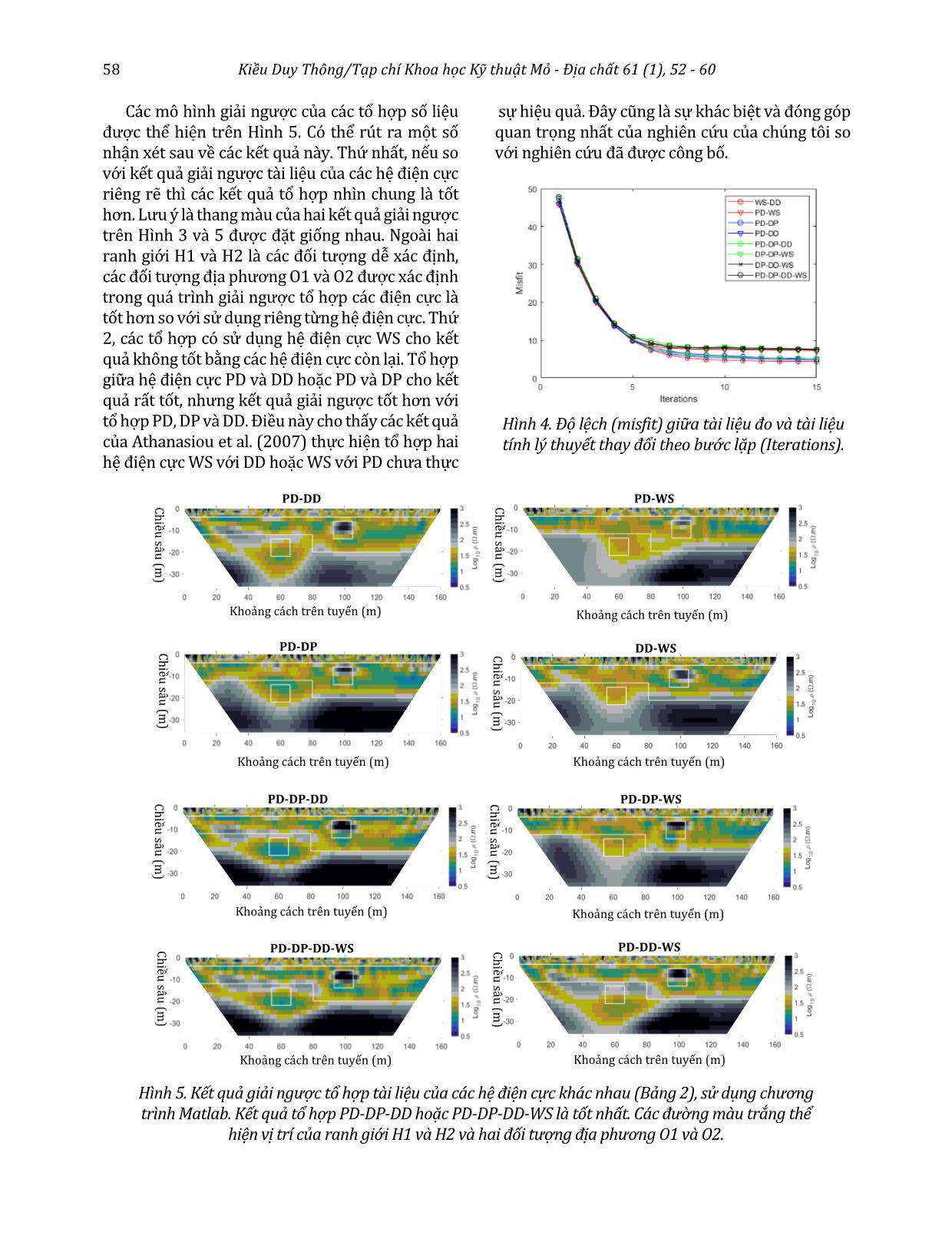
i). 
2.2. Giải ngược tổ hợp tài liệu điện trở suất từ 
các hệ điện cực 
Trong phương pháp điện trở suất sử dụng rất nhiều hệ điện cực khác nhau (Szalai and Szarka, 2008). Mỗi loại hệ điện cực có ưu điểm và nhược 
điểm riêng, tùy thuộc vào mô hình địa điện (Athanasiou et al., 2007; Dahlin and Zhou, 2004, 2006; Szalai et al., 2011). Trên thực tế phương 
pháp điện trở suất thường sử dụng các hệ điện cực 
được mô tả trong Hình 1. Trong trường hợp tổng quát, hệ điện cực WS thường có độ phân giải đứng tốt, ngược lại độ phân giải ngang của các hệ điện cực DD, PD và DP tốt hơn (Dahlin and Zhou, 2004). Chiều sâu nghiên cứu của hệ điện cực PD hoặc DP tốt hơn hệ điện cực DD và hệ điện cực WS (Szalai et al., 2011). Tuy nhiên ảnh hưởng của các bất 
đồng nhất địa phương gần mặt đất, thường không 
liên quan đến đối tường nghiên cứu lại tăng dần từ hệ điện cực WS, đến PD hoặc DP và cao nhất đối với hệ điện cực DD (Dahlin and Zhou, 2004). Do vậy, giải ngược tổ hợp tài liệu của các hệ điện cực 
có thể cho kết quả tốt hơn giải ngược tài liệu của từng hệ điện cực riêng lẻ, vì có thể tận dụng ưu 
điểm của hệ điện cực này để bù đắp nhược điểm của hệ điện cực kia. 
Do điện trở suất biểu kiến của cùng một mô 
hình địa điện sẽ phụ thuộc vào hệ điện cực sử dụng. Để tránh việc giá trị điện trở suất biểu kiến của hệ điện cực này chiếm vai trò quyết định trong quá trình giải ngược tổ hợp. Ví dụ trong trường hợp hệ điện cực DD thường có ảnh hưởng quyết 
định đến quá trình giải ngược tổ hợp (Athanasiou et al., 2007), nên phải thiết lập một hệ số cân bằng. Trong công trình của Athanasiou et al. (2007), các tác giả dựa vào độ nhạy mô hình, hay ma trận 
Jacobian để tính hệ số này. Kết quả của công trình này cho thấy, rất khó để đánh giá hiệu quả sử dụng hệ số cân bằng. Chúng tôi cho rằng nguyên nhân 
có thể là do việc tính hệ số này theo độ nhạy mô hình là không phù hợp, vì bản chất của hệ số cân bằng này phải liên quan đến điện trở suất biểu kiến. Do vậy, trong nghiên cứu này chúng tôi sử dụng cách tính hệ số cân bằng dựa vào điện trở 
(5) 
(8) 
(6) 
(7) 
(9) 
C1 C2 P2 P1 Wenner - Schlumberger (WS) 
C1 C2 P2 P1 Dipole - Dipole (DD) C2 
C1 P2 Pole - Dipole (PD) P1 
C1 P2 Dipole - Pole (DP) 
Hình 1: Các hệ điện cực thường dùng: Wenner - Schlumberger (WS), lưỡng cực trục (DD), ba cực thuận 
(PD), và ba cực nghịch (DP). 
56 Kiều Duy Thông/Tạp chí Khoa học Kỹ thuật Mỏ - Địa chất 61 (1), 52 - 60 suất biểu kiến, kỹ thuật này được đề xuất bởi Vozoff and Jupp (1975b). 
3. Kết quả và thảo luận 
3.1. Mô hình Trong nghiên cứu này chúng tôi thiết lập một mô hình lý thuyết (Hình 2). Giá trị điện trở suất của mô hình này được chia làm 4 nhóm và được 
tính như trong Bảng 1. Có thể thấy 4 nhóm điện trở bao gồm nhóm điện trở suất thấp (Res1), 
nhóm điện trở suất trung bình (Res2), nhóm điện trở suất cao (Res3) và nhóm điện trở suất rất cao (Res4). Trong mô hình này (Hình 1), giá trị của các khối trong mô hình được sắp xếp ngẫu nhiên. Lớp trên cùng gồm giá trị điện trở suất của hai nhóm Res2 và Res3. Lớp này đặc trưng cho lớp phủ, 
thường có có giá điện trở suất thay đổi mạnh. Lớp thứ hai có giá trị điện trở suất của nhóm Res2, và lớp cuối cùng có giá trị điện trở suất của nhóm Res3. Hai khối bất đồng nhất địa phương O1 và O2 
có giá trị điện trở suất thấp Res1 và rất cao Res4. Số liệu tính từ mô hình này được cộng thêm phần nhiễu ngẫu nhiên, 5% giá trị điện trở suất biểu
 kiến, cho số liệu mô phỏng gần với thực tế. 
Nhóm Công thức tính Giá trị điện trở suất (Ωm) 
1 𝑅𝑅𝑅𝑅𝑠𝑠1= 10�𝑟𝑟𝑟𝑟𝑟𝑟𝑑𝑑5 −0.5� 1.01 1.07 1.29 1.08 
2 𝑅𝑅𝑅𝑅𝑠𝑠2= 10�𝑟𝑟𝑟𝑟𝑟𝑟𝑑𝑑5 +1� 45.21 42.15 46.24 31.25 
3 𝑅𝑅𝑅𝑅𝑠𝑠3= 10�𝑟𝑟𝑟𝑟𝑟𝑟𝑑𝑑5 +2� 314.43 339.80 473.00 326.74 
4 𝑅𝑅𝑅𝑅𝑠𝑠4= 10�𝑟𝑟𝑟𝑟𝑟𝑟𝑑𝑑5 +3.1� 1622.43 1371.76 1941.15 1973.72 
Bảng 1. Giá trị điện trở suất trong mô hình (Hình 
2). Trong đó rand là hàm ngẫu nhiên. Giá trị điện 
trở suất của 4 nhóm được ký hiệu Res1, Res2, Res3, 
và Res4. 
(b) 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) (a) Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
(c) 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) (d) Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
(e) O2 
 Điện trở suất (Ωm) 
O1 L1 H2 H1 L2 L3 
Res1 Res2 Res3 Res4 
Hình 2. Mô hình địa điện (e) bao gồm ba lớp L1, L2 và L3 được phân chia bởi hai ranh giới H1 và H2 (các 
đường màu đỏ), có hai khối bất đồng nhất địa phương O1 và O2.Giá trị điện trở suất mô hình thể hiện 
trong Bảng 1. Giá trị điện trở suất biểu kiến tính từ mô hình cộng với 5% nhiễu ngẫu nhiên bởi các hệ điện 
cực DD (a), PD (b), DP (c) và WS (d) được thực hiện bằng phần mềm Res2dmod [23]. Khoảng cách giữa 
hai điện cực liên tiếp là 4.0 m. Trong các hình (a), (b), (c) và (d) dải màu thể hiện giá trị logarit cơ số 10 
điện trở suất biểu kiến; các chấm màu đen thể hiện vị trí điểm lấy số liệu. 
 Kiều Duy Thông/Tạp chí Khoa học Kỹ thuật Mỏ - Địa chất 61 (1), 52 - 60 57 Trong mô hình này việc sử dụng tài liệu đo điện trở suất để xác định các ranh giới H1 và H2 là tương 
đối dễ ràng, tuy nhiên việc xác định các đối tượng O1 và O2 là rất khó khăn, nhất là O1. Thứ nhất là ảnh 
hưởng bất đồng nhất lớp trên cùng L1. Thứ hai, đối 
tượng O1 tuy có điện trở suất khác biệt lớn so với 
môi trường vây quanh, nhưng do nằm ở chiều sâu lớn và nằm ngay dưới lớp L2 có điện trở suất thấp. Do vậy, một trong những điểm quan trọng nhất 
trong bài toán này là đánh giá xem liệu các hệ điện cực phát hiện các đối tượng O1 và O2 như thế nào. 
3.2. Kết quả giải ngược 
3.2.1. Kết quả giải ngược cho từng hệ điện cực 
Để kiểm chứng hiệu quả của việc kết hợp các hệ điện cực. Đầu tiên chúng tôi chạy giải ngược cho từng hệ điện cực, sử dụng phần mềm đang 
được sử dụng rộng rãi trên thế giới, Res2dinv [23]. Kết quả được thể hiện trên Hình 3. Các kết quả này cho thấy nhìn chung các ranh giới H1 và H2 phân chia giữa các lớp L1, L2 và L3 được thể hiện trên các mô hình giải ngược của cả bốn hệ 
điện cực. Đối tượng O2 có thể nhìn thấy trên các 
mô hình này, nhưng đối tượng O1 trong tất cả các 
trường hợp đều không rõ ràng. Đối tượng O1 này tạo thành một đới dị thường điện trở suất thấp ở các kết quả của hệ điện cực DD, PD và DP giống 
như dị thường của đới đứt gãy, thậm chí O1 không thấy thể hiện trong kết quả của hệ điện cực WS. 
3.2.2. Kết quả giải ngược tổ hợp Các kết quả giải ngược này được thực hiện bằng chương trình Matlab. Chúng tôi đã thay đổi 
chương trình từ chương trình gốc được công bố bởi Akca (2016) cho các quá trình giải ngược của bài báo này. Tổ hợp số liệu của các hệ điện cực 
được trình bày trong Bảng 2. Trên Hình 4 thể hiện 
độ lệch (misfit) giữa số liệu tính toán lý thuyết và tài liệu đo thực tế (ở đây là tài liệu tính theo mô hình cộng với nhiễu ngẫu nhiên). Giá trị độ lệch càng nhỏ thể hiện số liệu tính lý thuyết và số liệu 
đo càng gần nhau. Độ lệch này suy giảm một cách 
ổn định theo các bước lặp thể hiện chương trình giải ngược làm việc tốt. Nhìn chung sự khác biệt 
độ lệch giữa các tổ hợp số liệu của các điện cực là không nhiều, và đề nằm trong mức nhiễu 5%. Cần 
lưu ý là độ lệch nhỏ hơn không đảm bảo kết quả giải ngược tốt hơn, mà chỉ cần độ lệch này tương 
đương mức nhiễu là được (Constable et al., 2015). 
 TT Ký hiệu Tổ hợp số liệu của các hệ điện cực TT Ký hiệu Tổ hợp số liệu của các hệ điện cực 1 PD-DD PD và DD 5 PD-DP-DD PD; DP; và DD 2 PD-DP PD và DP 6 PD-DP-WS PD; DP và WS 3 PD-WS PD và WS 7 PD-DD-WS PD; DD; và WS 4 WS-DD WS và DD 8 PD-DP-DD-WS PD; DP; DD; và WS 
DP 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
DD 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
PD 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
WS 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
Hình 3. Kết quả giải ngược tài liệu của các hệ điện cực khác nhau, sử dụng phần mềm Res2dinv [23]. Các 
đường màu trắng thể hiện vị trí của ranh giới H1 và H2 và hai đối tượng địa phương O1 và O2. 
Bảng 2. Ký hiệu các tổ hợp số liệu từ các hệ điện cực khác nhau. Lưu ý viết tắt của các hệ điện cực xem 
trong Hình 1. 
58 Kiều Duy Thông/Tạp chí Khoa học Kỹ thuật Mỏ - Địa chất 61 (1), 52 - 60 Các mô hình giải ngược của các tổ hợp số liệu 
được thể hiện trên Hình 5. Có thể rút ra một số nhận xét sau về các kết quả này. Thứ nhất, nếu so với kết quả giải ngược tài liệu của các hệ điện cực riêng rẽ thì các kết quả tổ hợp nhìn chung là tốt 
hơn. Lưu ý là thang màu của hai kết quả giải ngược 
trên Hình 3 và 5 được đặt giống nhau. Ngoài hai ranh giới H1 và H2 là các đối tượng dễ xác định, 
các đối tượng địa phương O1 và O2 được xác định trong quá trình giải ngược tổ hợp các điện cực là tốt hơn so với sử dụng riêng từng hệ điện cực. Thứ 2, các tổ hợp có sử dụng hệ điện cực WS cho kết quả không tốt bằng các hệ điện cực còn lại. Tổ hợp giữa hệ điện cực PD và DD hoặc PD và DP cho kết quả rất tốt, nhưng kết quả giải ngược tốt hơn với tổ hợp PD, DP và DD. Điều này cho thấy các kết quả của Athanasiou et al. (2007) thực hiện tổ hợp hai hệ điện cực WS với DD hoặc WS với PD chưa thực
 sự hiệu quả. Đây cũng là sự khác biệt và đóng góp quan trọng nhất của nghiên cứu của chúng tôi so với nghiên cứu đã được công bố. 
Hình 4. Độ lệch (misfit) giữa tài liệu đo và tài liệu 
tính lý thuyết thay đổi theo bước lặp (Iterations). 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
Khoảng cách trên tuyến (m) 
PD-DP 
Khoảng cách trên tuyến (m) 
PD-DP-WS 
Khoảng cách trên tuyến (m) 
PD-DP-DD Chiều sâu (m) 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
Khoảng cách trên tuyến (m) 
DD-WS 
Chiều sâu (m) 
PD-DP-DD-WS PD-DD-WS 
PD-WS PD-DD 
Khoảng cách trên tuyến (m) 
Chiều sâu (m) 
Chiều sâu (m) 
Chiều sâu (m) 
Hình 5. Kết quả giải ngược tổ hợp tài liệu của các hệ điện cực khác nhau (Bảng 2), sử dụng chương 
trình Matlab. Kết quả tổ hợp PD-DP-DD hoặc PD-DP-DD-WS là tốt nhất. Các đường màu trắng thể 
hiện vị trí của ranh giới H1 và H2 và hai đối tượng địa phương O1 và O2. 
 Kiều Duy Thông/Tạp chí Khoa học Kỹ thuật Mỏ - Địa chất 61 (1), 52 - 60 59 
4. Kết luận Kết quả từ mô hình lý thuyết cho thấy giải 
ngược tổ hợp số liệu của các hệ điện cực cho mô hình tốt hơn so với mô hình của từng hệ điện cực riêng lẻ. Sử dụng tổ hợp số liệu các hệ điện cực đòi hỏi chi phí thực địa và tính toán cao hơn. Tuy 
nhiên đây không thực sự là vấn đề lớn nhờ sự phát triển của công nghệ đo đạc và sức mạnh của các máy tính hiện nay. Kết quả này chỉ ra rằng tổ hợp giữa hệ điện cực: cực - lưỡng cực (PD), lưỡng cực - cực (DP) và lưỡng cực - lưỡng cực (DD) với mô hình dạng này cho kết quả tốt nhất. Trong nghiên cứu này chúng tôi mới tiến hành thử nghiệm trên tài liệu lý thuyết, dù cho đã được mô phỏng rất gần với điều kiện thực tế. Trong các nghiên cứu tiếp theo chúng tôi sẽ thử nghiệm trên tài liệu đo thực tế để đánh giá chính xác hơn khả năng áp dụng vào thực tế sản xuất của phương pháp này. 
Lời cảm ơn Bài báo này hoàn thành là kết quả của đề tài cấp 
cơ sở Trường Đại học Mỏ - Địa chất, mã số T18-36. Bản quyền phần mềm Matlab được tài trợ bởi công ty RoqSense. Chúng tôi chân thành cảm ơn Akca tác giả của bài báo “ELRIS2D: A MATLAB Package for the 2D Inversion of DC Resistivity/IP 
Data” đã cung cấp mã nguồn cho chương trình giải 
ngược tài liệu điện trở hai chiều. Chúng tôi trân trọng cảm ơn tiến sỹ Loke, người đã phát triển các phần mềm Res2dmod và Res2dinv và cung cấp các bản dùng miễn phí với mục đích nghiên cứu. 
Tài liệu tham khảo Akca, I., (2016). ELRIS2D: A MATLAB Package for the 2D Inversion of DC Resistivity/IP Data, 
Acta Geophysica 64. 443. Athanasiou, E. N., Tsourlos, P. I., Papazachos, C. B., and Tsokas, G. N., (2007). Combined weighted inversion of electrical resistivity data arising from different array types: Journal of Applied 
Geophysics 62(2). 124 - 140. Constable, S. C., Parker, R. L., and Constable, C. G., (1987). Occam's inversion; a practical algorithm for generating smooth models from electromagnetic sounding data: Geophysics 52(3) 3. 289 - 300. 
Constable, S., Orange, A., and Key, K., (2015). And the geophysicist replied: “Which model do you want?”: Geophysics 80(3). E(197-E212). Dahlin, T., and Zhou, B., (2004). A numerical comparison of 2D resistivity imaging with 10 electrode arrays: Geophysical Prospecting, v. 52, no. 5, p. 379-398.-, (2006), Multiple-gradient array measurements for multichannel 2D resistivity imaging: Near 
Surface Geophysics 4(2). 113 - 123. Gallardo, L. A., and Meju, M. A., (2011). Structure-coupled multiphysics imaging in geophysical sciences: Reviews of Geophysics 49(1). Heincke, B., Jegen, M., Moorkamp, M., Hobbs, R. W., and Chen, J., (2017). An adaptive coupling strategy for joint inversions that use petrophysical information as constraints: 
Journal of Applied Geophysics 136. 279 - 297. Lines, L., Schultz, A., and Treitel, S., (1988). Cooperative inversion of geophysical data: 
Geophysics 53(1). 8 - 20. Menke, W., (2015). Review of the Generalized Least Squares Method: Surveys in Geophysics 36(1). 1 - 25. Moorkamp, M., (2017). Integrating Electromagnetic Data with Other Geophysical Observations for Enhanced Imaging of the Earth: A Tutorial and Review: Surveys in 
Geophysics. Moorkamp, M., Heincke, B., Jegen, M., Roberts, A. W., and Hobbs, R. W., (2011). A framework for 3-D joint inversion of MT, gravity and seismic refraction data: Geophysical Journal 
International 184(1). 477 - 493. Paasche, H., and Tronicke, J., (2007). Cooperative inversion of 2D geophysical data sets: a zonal approach based on fuzzy c-means cluster analysis: Geophysics 72(3). 35 - 39. Sun, J., and Li, Y., (2014). Adaptive Lp inversion for simultaneous recovery of both blocky and smooth features in a geophysical model: 
Geophysical Journal International 197(2). 882 -899; (2015), Multidomain petrophysically constrained inversion and geology differentiation using guided fuzzy c-means clustering: Geophysics 80(4). ID1-ID18.
60 Kiều Duy Thông/Tạp chí Khoa học Kỹ thuật Mỏ - Địa chất 61 (1), 52 - 60 Szalai, S., and Szarka, L., (2008). On the classification of surface geoelectric arrays: 
Geophysical Prospecting 56(2). 159 - 175. Szalai, S., Novák, A., and Szarka, L., (2011). Which geoelectric array sees the deepest in a noisy environment? Depth of detectability values of multielectrode systems for various two-dimensional models: Physics and Chemistry of 
the Earth, Parts A/B/C 36(16). 1398 - 1404. Tarantola, A., and Valette, B., (1982). Generalized nonlinear inverse problems solved using the least squares criterion: Reviews of Geophysics 20(2). 19 - 232. 
Tikhonov, A. N., and Arsenin, V. I. A., (1977). Solutions of ill-posed problems, Winston. Thông, K. D., (2018). Tổng quan về giải ngược tổ hợp tài liệu địa vật lý, Hội nghị toàn quốc về khoa học trái đất và phát triển bền vững (ERSD). Trường, Đại học Mỏ - Địa chất. Vozoff, K., and Jupp, D. L. B., (1975a). Joint Inversion of Geophysical Data: Geophysical 
Journal of the Royal Astronomical Society, v. 42, no. 3, p. 977-991.-, (1975b, Joint Inversion of 
Geophysical Data 42(3). 977 - 991.