Improving stability for independent power control of dfig with sfoc and dpc during grid unbalance

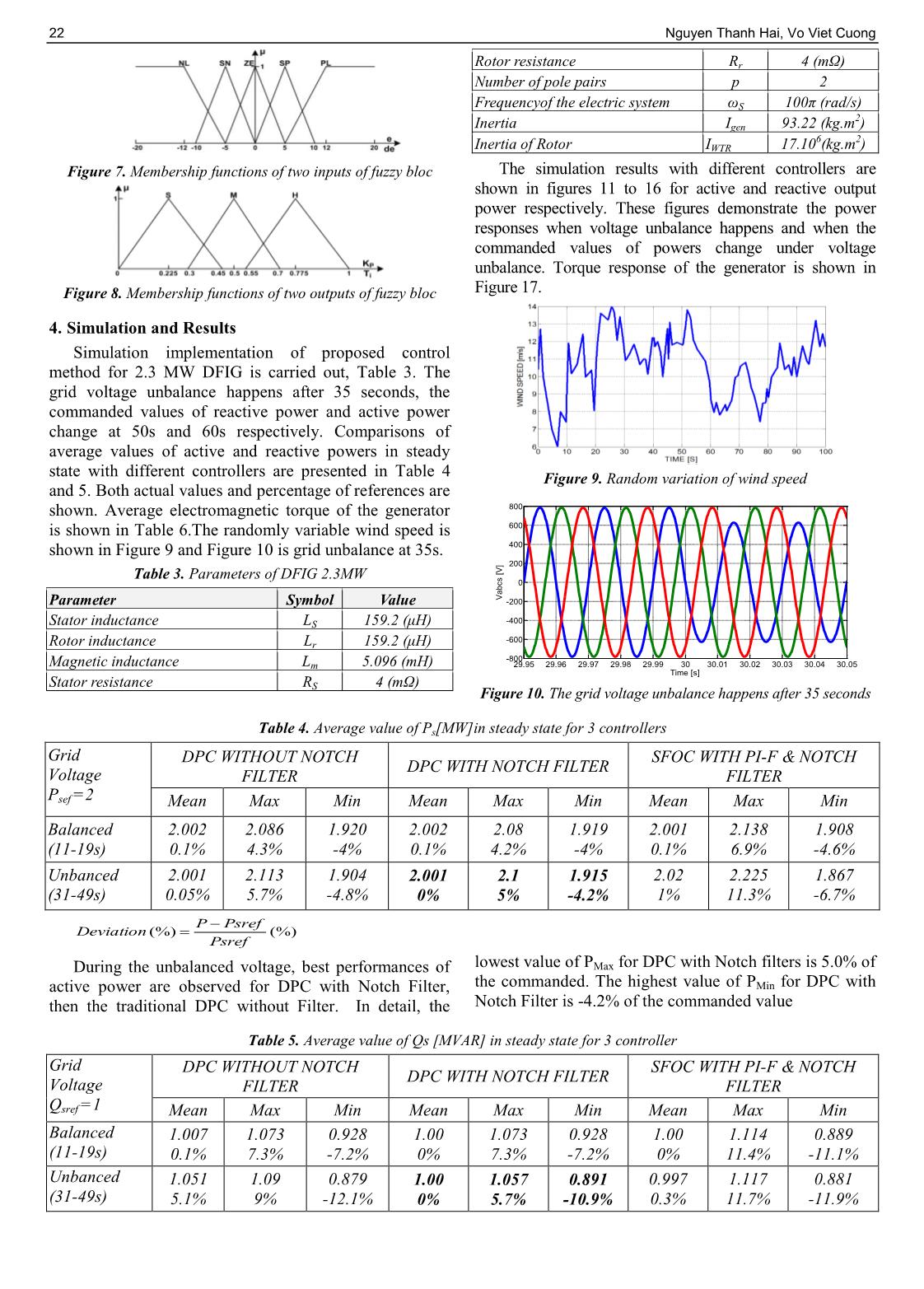
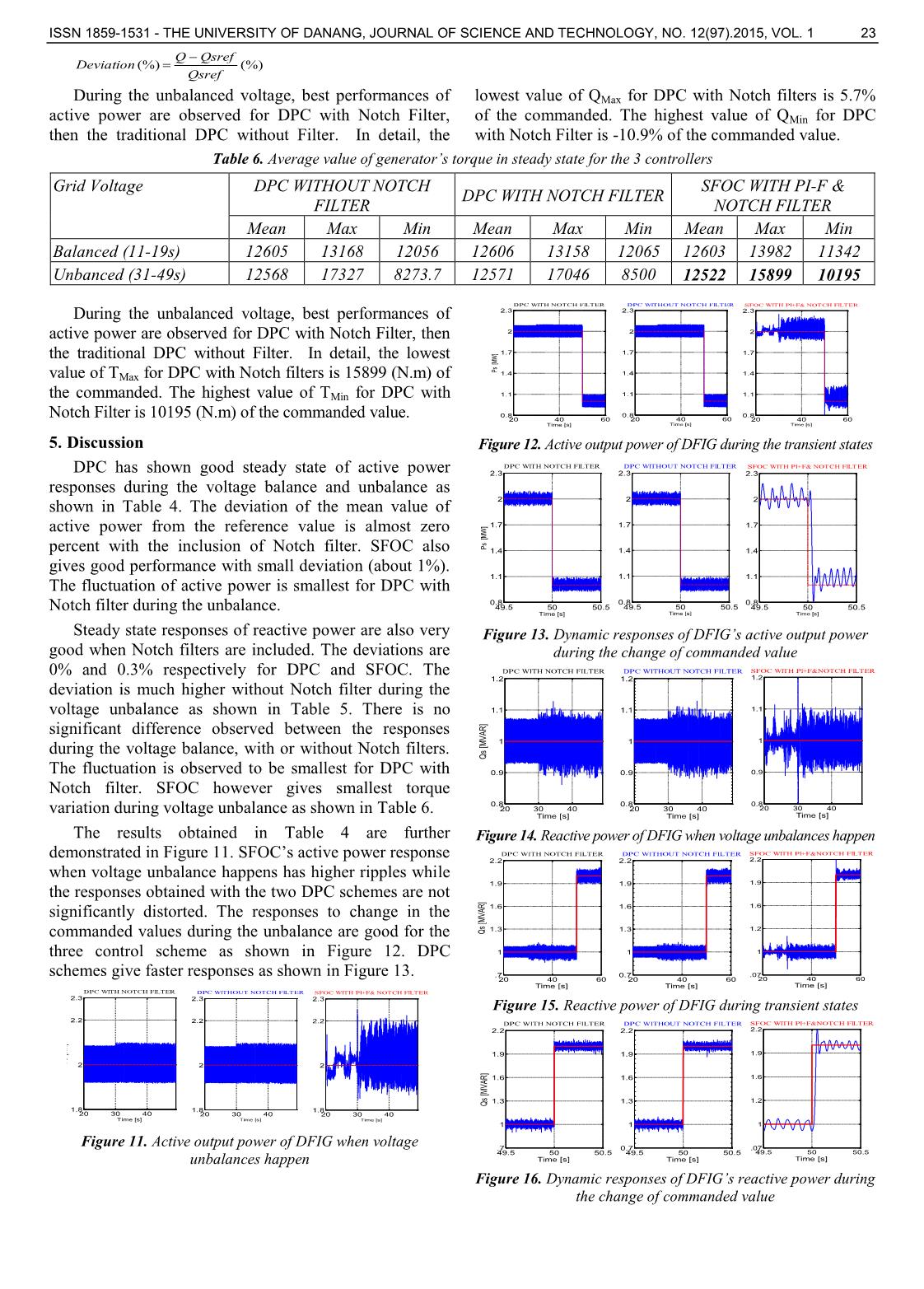
oposed control scheme for the RSC 
of a DFIG using PI+F controller and Notch filters 
In both control scheme in Figure 3, Notch filters are 
used to eliminate second order harmonic components in 
positive and negative sequences of stator voltage. In 
Figure 4, Notch filters are used with positive sequences of 
stator voltage and rotor current. 
Figure 5 shows the spatial relationships between the 
stationary (α,β)s reference frame, the rotor (α,β)r reference 
frame rotating at the speed of ωr, and the dq+ and dq− 
reference frames rotating at the angular speed of ωs and 
−ωs, respectively. As shown, the d
+
-axis of the dq
+ 
reference frame is fixed to the positive sequence stator 
voltage V
+
sd+. 
According to Figure 5, the transformations between 
(α,β)s, (α,β)r and dq+ and dq− reference frames are given by 
2
( ) ( )
slip slip
rr r
j t j t
dq dqI I e I e
 
  
 (3) 
2
( ) ( )
slip slip
rr r
j t j t
dq dqI I e I e
 
  
 (4) 
 ( ) ( ) ( )I t I t I t    (5) 
s
s s s
dq
dq s dq s dq
d
V R I j
dt

 
 (6) 
 2 slip
r r r r r
j t
d d d d dI I I I I e
 
 [6; 7; 8] (7) 
 2 slipr r r r r
j t
q q q q qI I I I I e
 
 [6; 7; 8] (8) 
Active and reactive power of stator: 
3 3
( )
2 2
s s s s r
m
s d d q q s q
s
L
P v i v i V i
L
 (9) 
 3 3( )
2 2
s s s s r
sm
s q d d q s q
s s m
VL
Q v i v i V i
L L
 (10) 
PI-Fuzzy controllers as shown in Figure 6 are used to 
control the errors between the required and actual values of 
both the active power and reactive power delivered to the 
grid by the generator. The parameters of the PI-Fuzzy are 
adjusted by the fuzzy rules to obtain the best output to drive 
the errors to zero. The variable parameters of the controllers, 
which are fixed in traditional PI controllers, will help to 
achieve the best performance of the system. The outputs of 
these controllers are commanded values of d-q components 
of rotor current in the stator flux oriented reference frame. 
These commanded values of currents are used to regulate the 
RSC for provision of the rotor phase voltage to DFIG. 
The fuzzy rules for parameters of PI-FUZZY 
controllers are presented in Table 1 and Table 2. The rules 
are developed by trial and error method. LN, SN, ZE, SP, 
and LP represents large negative, small negative, zero, 
small positive and large positive respectively. S, M, H 
stand for small, medium and high respectively. 
Table 1. rule base of Kp [5] Table 2. rule base of Ti [5] 
Kp 
de/dt 
Ti 
de/dt 
LN SN ZE SP LP LN SN ZE SP LP 
e 
LN H H H H H 
e 
LN H H H H H 
SN H M M M H SN H M M M H 
ZE M S S S M ZE H M S M H 
SP M M M M H SP H M M M H 
LP M H H H H LP H H H H H 
Figure 5. Relationships between (α,β)s, (α,β)rand 
dq+ and dq− reference frames [6] 
Figure 6. PI-Fuzzy controller 
The triangular membership functions of inputs and 
outputs of PI-Fuzzy controller are shown in Figure 7, 8: 
22 Nguyen Thanh Hai, Vo Viet Cuong 
Figure 7. Membership functions of two inputs of fuzzy bloc 
Figure 8. Membership functions of two outputs of fuzzy bloc 
4. Simulation and Results 
Simulation implementation of proposed control 
method for 2.3 MW DFIG is carried out, Table 3. The 
grid voltage unbalance happens after 35 seconds, the 
commanded values of reactive power and active power 
change at 50s and 60s respectively. Comparisons of 
average values of active and reactive powers in steady 
state with different controllers are presented in Table 4 
and 5. Both actual values and percentage of references are 
shown. Average electromagnetic torque of the generator 
is shown in Table 6.The randomly variable wind speed is 
shown in Figure 9 and Figure 10 is grid unbalance at 35s. 
Table 3. Parameters of DFIG 2.3MW 
Parameter Symbol Value 
Stator inductance LS 159.2 (μH) 
Rotor inductance Lr 159.2 (μH) 
Magnetic inductance Lm 5.096 (mH) 
Stator resistance RS 4 (mΩ) 
Rotor resistance Rr 4 (mΩ) 
Number of pole pairs p 2 
Frequencyof the electric system ωS 100π (rad/s) 
Inertia Igen 93.22 (kg.m
2) 
Inertia of Rotor IWTR 17.10
6(kg.m2) 
The simulation results with different controllers are 
shown in figures 11 to 16 for active and reactive output 
power respectively. These figures demonstrate the power 
responses when voltage unbalance happens and when the 
commanded values of powers change under voltage 
unbalance. Torque response of the generator is shown in 
Figure 17. 
Figure 9. Random variation of wind speed 
Figure 10. The grid voltage unbalance happens after 35 seconds 
Table 4. Average value of Ps[MW]in steady state for 3 controllers 
Grid 
Voltage 
Psef =2 
DPC WITHOUT NOTCH 
FILTER 
DPC WITH NOTCH FILTER 
SFOC WITH PI-F & NOTCH 
FILTER 
Mean Max Min Mean Max Min Mean Max Min 
Balanced 
(11-19s) 
2.002 
0.1% 
2.086 
4.3% 
1.920 
-4% 
2.002 
0.1% 
2.08 
4.2% 
1.919 
-4% 
2.001 
0.1% 
2.138 
6.9% 
1.908 
-4.6% 
Unbanced 
(31-49s) 
2.001 
0.05% 
2.113 
5.7% 
1.904 
-4.8% 
2.001 
0% 
2.1 
5% 
1.915 
-4.2% 
2.02 
1% 
2.225 
11.3% 
1.867 
-6.7% 
During the unbalanced voltage, best performances of 
active power are observed for DPC with Notch Filter, 
then the traditional DPC without Filter. In detail, the 
lowest value of PMax for DPC with Notch filters is 5.0% of 
the commanded. The highest value of PMin for DPC with 
Notch Filter is -4.2% of the commanded value 
Table 5. Average value of Qs [MVAR] in steady state for 3 controller 
Grid 
Voltage 
Qsref =1 
DPC WITHOUT NOTCH 
FILTER 
DPC WITH NOTCH FILTER 
SFOC WITH PI-F & NOTCH 
FILTER 
Mean Max Min Mean Max Min Mean Max Min 
Balanced 
(11-19s) 
1.007 
0.1% 
1.073 
7.3% 
0.928 
-7.2% 
1.00 
0% 
1.073 
7.3% 
0.928 
-7.2% 
1.00 
0% 
1.114 
11.4% 
0.889 
-11.1% 
Unbanced 
(31-49s) 
1.051 
5.1% 
1.09 
9% 
0.879 
-12.1% 
1.00 
0% 
1.057 
5.7% 
0.891 
-10.9% 
0.997 
0.3% 
1.117 
11.7% 
0.881 
-11.9% 
29.95 29.96 29.97 29.98 29.99 30 30.01 30.02 30.03 30.04 30.05
-800
-600
-400
-200
0
200
400
600
800
Time [s]
V
a
b
c
s
 [
V
]
%)( %)( 
Psref
PsrefP
Deviation
ISSN 1859-1531 - THE UNIVERSITY OF DANANG, JOURNAL OF SCIENCE AND TECHNOLOGY, NO. 12(97).2015, VOL. 1 23 
During the unbalanced voltage, best performances of 
active power are observed for DPC with Notch Filter, 
then the traditional DPC without Filter. In detail, the 
lowest value of QMax for DPC with Notch filters is 5.7% 
of the commanded. The highest value of QMin for DPC 
with Notch Filter is -10.9% of the commanded value. 
Table 6. Average value of generator’s torque in steady state for the 3 controllers 
Grid Voltage DPC WITHOUT NOTCH 
FILTER 
DPC WITH NOTCH FILTER 
SFOC WITH PI-F & 
NOTCH FILTER 
Mean Max Min Mean Max Min Mean Max Min 
Balanced (11-19s) 12605 13168 12056 12606 13158 12065 12603 13982 11342 
Unbanced (31-49s) 12568 17327 8273.7 12571 17046 8500 12522 15899 10195 
During the unbalanced voltage, best performances of 
active power are observed for DPC with Notch Filter, then 
the traditional DPC without Filter. In detail, the lowest 
value of TMax for DPC with Notch filters is 15899 (N.m) of 
the commanded. The highest value of TMin for DPC with 
Notch Filter is 10195 (N.m) of the commanded value. 
5. Discussion 
DPC has shown good steady state of active power 
responses during the voltage balance and unbalance as 
shown in Table 4. The deviation of the mean value of 
active power from the reference value is almost zero 
percent with the inclusion of Notch filter. SFOC also 
gives good performance with small deviation (about 1%). 
The fluctuation of active power is smallest for DPC with 
Notch filter during the unbalance. 
Steady state responses of reactive power are also very 
good when Notch filters are included. The deviations are 
0% and 0.3% respectively for DPC and SFOC. The 
deviation is much higher without Notch filter during the 
voltage unbalance as shown in Table 5. There is no 
significant difference observed between the responses 
during the voltage balance, with or without Notch filters. 
The fluctuation is observed to be smallest for DPC with 
Notch filter. SFOC however gives smallest torque 
variation during voltage unbalance as shown in Table 6. 
The results obtained in Table 4 are further 
demonstrated in Figure 11. SFOC’s active power response 
when voltage unbalance happens has higher ripples while 
the responses obtained with the two DPC schemes are not 
significantly distorted. The responses to change in the 
commanded values during the unbalance are good for the 
three control scheme as shown in Figure 12. DPC 
schemes give faster responses as shown in Figure 13. 
Figure 11. Active output power of DFIG when voltage 
unbalances happen 
Figure 12. Active output power of DFIG during the transient states 
Figure 13. Dynamic responses of DFIG’s active output power 
during the change of commanded value 
Figure 14. Reactive power of DFIG when voltage unbalances happen 
Figure 15. Reactive power of DFIG during transient states 
Figure 16. Dynamic responses of DFIG’s reactive power during 
the change of commanded value 
%)( %)( 
Qsref
QsrefQ
Deviation
20 30 40
1.8
2
2.2
2.3
DPC WITHOUT NOTCH FILTER
Time [s]
20 30 40
1.8
2
2.2
2.3
SFOC WITH PI+F& NOTCH FILTER
Time [s]
20 30 40
1.8
2
2.2
2.3
Time [s]
P
s 
 [M
W
]
DPC WITH NOTCH FILTER
20 40 60
0.8
1.1
1.4
1.7
2
2.3
DPC WITHOUT NOTCH FILTER
Time [s]
20 40 60
0.8
1.1
1.4
1.7
2
2.3
SFOC WITH PI+F& NOTCH FILTER
Time [s]
20 40 60
0.8
1.1
1.4
1.7
2
2.3
Time [s]
Ps
 [
M
W
]
DPC WITH NOTCH FILTER
49.5 50 50.5
0.8
1.1
1.4
1.7
2
2.3
DPC WITHOUT NOTCH FILTER
Time [s]
49.5 50 50.5
0.8
1.1
1.4
1.7
2
2.3
SFOC WITH PI+F& NOTCH FILTER
Time [s]
49.5 50 50.5
0.8
1.1
1.4
1.7
2
2.3
Time [s]
P
s 
 [M
W
]
DPC WITH NOTCH FILTER
20 30 40
0.8
0.9
1
1.1
1.2
Time [s]
Q
s 
[M
V
A
R
]
DPC WITH NOTCH FILTER
20 30 40
0.8
0.9
1
1.1
1.2
DPC WITHOUT NOTCH FILTER
Time [s]
20 30 40
0.8
0.9
1
1.1
1.2
SFOC WITH PI+F&NOTCH FILTER
Time [s]
20 40 60
.7
1
1.3
1.6
1.9
2.2
Time [s]
Q
s 
[M
VA
R
]
DPC WITH NOTCH FILTER
20 40 60
0.7
1
1.3
1.6
1.9
2.2
DPC WITHOUT NOTCH FILTER
Time [s]
20 40 60
.07
1
1.2
1.6
1.9
2.2
SFOC WITH PI+F&NOTCH FILTER
Time [s]
49.5 50 50.5
.7
1
1.3
1.6
1.9
2.2
Time [s]
Q
s 
[M
V
A
R
]
DPC WITH NOTCH FILTER
49.5 50 50.5
0.7
1
1.3
1.6
1.9
2.2
DPC WITHOUT NOTCH FILTER
Time [s]
49.5 50 50.5
.07
1
1.2
1.6
1.9
2.2
SFOC WITH PI+F&NOTCH FILTER
Time [s]
24 Nguyen Thanh Hai, Vo Viet Cuong 
Figure 17. Torque of DFIG 
Higher ripples are also observed in reactive power 
responses of SFOC when voltage unbalance occurs as 
shown in Figure 14. The observation is consistent with 
statistics presented in Table 5. Reactive powers in the three 
control scheme follow the commanded values under the 
condition of voltage unbalance as shown in Figure 15. 
Time responses of reactive power in DPC control schemes 
are also less than those of SFOC as shown in Figure 16. 
Torque responses observed in Figure 17 are also 
consistent with the statistics shown in Table 6. 
6. Conclusion 
The proposed SFOC scheme for DFIG with the 
inclusion of PI-Fuzzy controllers and Notch filters has 
improved the stability of independent control of active 
and reactive power during grid voltage unbalance. The 
responses of active and reactive power are compared with 
a traditional DPC and modified DPC using Notch filters 
to increase the stability. The observations are made during 
the occurrence of voltage dip in one phase, transient states 
as well steady states of the powers under unbalanced 
condition. In all the observations, the independent control 
of the powers is maintained for the proposed scheme. 
However, high fluctuations in active and reactive 
powers are present in the responses obtained with the 
proposed scheme although lower ripples are observed for 
generator’s torque. 
Experimental verification of the new control scheme 
should be carried out to validate the results obtained with 
simulation. 
REFERENCES 
[1] Ackermann, T., Wind power in power systems, John Wiley and 
Sons, USA, 2003. 
[2] Leonhard, W., Control of electric drives, Springer-Verlag, 3rd 
edition, USA, 2001. 
[3] Muljadi, E., Yildirim, D., Batan, T., and Butterfield, C.P., 
“Understand the unbalanced-voltage problem in wind turbine 
generation”, Proceeding of IEEE Industry Application Conference, 
Phoenix, USA, 1999, pp.1359-1365. 
[4] Baggu, M. M.; “Advanced control techniques for doubly fed 
induction generator – based wind turbine converters to improve 
low voltage ride- throught during system imbalances”, PhD Thesis, 
Missouri University of Science and Technology, 2009. 
[5] Pham-Dinh, T., Pham-Trung, H., Le-Thanh, H., “PI-Fuzzy 
Controller for Doubly Fed Induction Generator Wind Turbine”, 
Proceedings of ASEAN Symposium on Automatic Control ASAC 
2011, Vietnam, 2011, pp.79 – 81. 
[6] Phan, V. T., Lee, H. H., Chun, T. W.; “An Effective rotor current controller 
for unbalanced stand – alone DFIG systems in the rotor reference frame”, 
Journal of Power electrionics, Vol.10, No.6, 2010, pp 194-202. 
[7] L. Xu, Y. Wang, “Dynamic modeling and control of DFIG based 
wind turbines under unbalanced network conditions”, IEEE Trans. 
Power Syst. 22 (1) (2007) 314–323. 
[8] A. Peterson, L. Harnefors, T. Thiringer, “Comparison between 
stator-flux and grid flux oriented rotor current control of doubly-
fed induction generators”, The 35th Annual IEEE Power 
Electronics Specialist Conference, vol. 1, 20–25 June,2004, pp. 
482–486. 
[9] Sorensen, P.; Hansen, D.A.; Christensen, P.; Mieritz, M.; Bech, J.; 
Bak-Jensen, B.; Nielsen, H.; “Simulation and Verification of 
Transient Events in Large Wind Power Installation”, Project 
Report, Risø National Laboratory, Roskilde, Norway; 2003. 
[10] Masters, M. G. Renewable and Efficient Electric Power Systems, 
John Wiley and Sons, Inc., Publication; 2004. 
[11] Jia-bing HU, Yi-kang HE; “Modeling and enhanced control of DFIG 
under unbalanced grid voltage conditions”, Electric Power Systems 
Research 79(2009); pp 273-281. 
[12] Hai Nguyen-Thanh; “Improved Control of DFIG Systems under 
Unbalanced Voltage Dip for Torque Stability Using PI-Fuzzy 
Controller”; International Journal of Electrical Energy, Vol. 2, No. 
4, December 2014; pp. 300-307, USA. 
(The Board of Editors received the paper on 15/05/2015, its review was completed on 05/07/2015) 
20 40 60 80
0
3
6
9
12
15
18
20
Time [s]
Te
 [ 
K
N
.m
]
DPC WITH NOTCH FILTER
20 40 60 80
0
3
6
9
12
15
18
20
DPC WITHOUT NOTCH FILTER
Time [s]
20 40 60 80
0
3
6
9
12
15
18
20
FOC WITH PI+F& NOTCH FILTER
Time [s]