Improving computing efficiency in electric power measurement using goertzel algorithm

i qua điểm 0. 
Nhờ công thức (28) có thể xác định được chu kỳ tín hiệu và thời điểm tín hiệu đi qua 
điểm 0 chính xác hơn. 
Sử dụng biến đổi Fourier nhanh FFT trong khoảng thời gian Ti xác định biên độ và pha 
của các sóng hài của tín hiệu dòng điện và điện áp. 
y 
t 
yi-1 
yi 
ym 
ym+1 
Ti 
ti 
ts 
th 
tm+1 
Transport and Communications Science Journal, Vol 72, Issue 2 (02/2021), 143-157 
149 
0 50 100 150 200 250
-150
-100
-50
0
50
100
150
Thoi gian 0.1ms
B
ie
n
 d
o
v(t)
i(t)
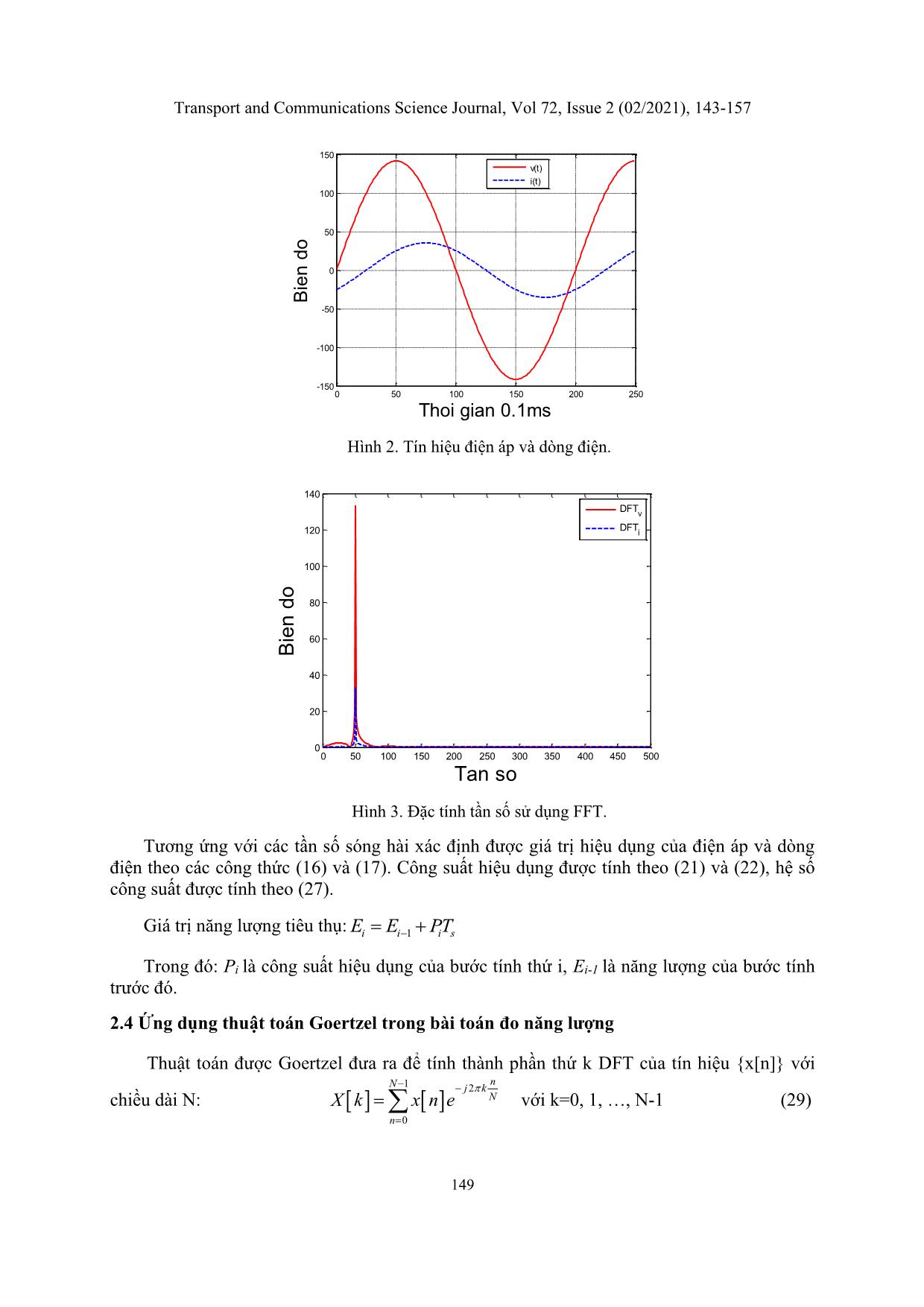
Hình 2. Tín hiệu điện áp và dòng điện. 
0 50 100 150 200 250 300 350 400 450 500
0
20
40
60
80
100
120
140
Tan so
B
ie
n
 d
o
DFT
v
DFT
i
Hình 3. Đặc tính tần số sử dụng FFT. 
Tương ứng với các tần số sóng hài xác định được giá trị hiệu dụng của điện áp và dòng 
điện theo các công thức (16) và (17). Công suất hiệu dụng được tính theo (21) và (22), hệ số 
công suất được tính theo (27). 
Giá trị năng lượng tiêu thụ:
1i i i sE E PT−= + 
Trong đó: Pi là công suất hiệu dụng của bước tính thứ i, Ei-1 là năng lượng của bước tính 
trước đó. 
2.4 Ứng dụng thuật toán Goertzel trong bài toán đo năng lượng 
Thuật toán được Goertzel đưa ra để tính thành phần thứ k DFT của tín hiệu {x[n]} với 
chiều dài N:    
1 2
0
nN j k
N
n
X k x n e
 − −
=
= với k=0, 1, , N-1 (29) 
Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 2 (02/2021), 143-157 
150 
Coi giá trị X[k] là tích chập của tín hiệu x[n] và hk[n]: 
      
1 2
0
m nN j k
N
k k
n
Y m x n e h m n
−−
=
= − (30) 
Như vậy: ( )  kY N X k= 
Như vậy thay bằng việc tính công thức (29) để tìm ra phổ tín hiệu thì tính đáp ứng ra của 
hệ thống tuyến tính IIR với đáp ứng xung {hk[n]} ở công thức (30). 
Để thuận tiện cho việc giải bài toán này, chuyển đổi sang miền z có: 
 ( )    
2 2
0
n n
j k j k
n n nN z
k k
n n n
H z h n z e u n z e z
− − −
=− =− =
= = =   (31) 
Biến đổi z ngược ta có phương trình sai phân: 
      
2
1
k
j
N
k kY n x n e Y n
= + − với  1 0kY − = (32) 
Đặt biến trung gian: 
1 2
( )
( )
2
1 2cos
X z
S z
k
z z
N
 − −
=
− + 
 (33) 
Sau một vài phép biến đổi ta có: 
  
( )
( )
( )
( )
( )
( )
2
1
1 2
1
1
2
1 2cos
k
j
k k N
k
Y z Y z S z
H z e z
kX z S z X z
z z
N
−
−
− −
= = = − 
 − + 
 (34) 
Như vậy để tính Yk[n] cần thực hiện qua 2 bước: 
- Tính        
2
2cos 1 2
k
S n x n S n S n
N
= + − − − 
 (35) 
- Tính      
2
1
k
j
N
kY n S n e S n
−
= − − (36) 
Với các điều kiện S[-2]= S[-1]=0 
Lúc này thuật toán (36) không hồi quy, giá trị của Yk[n] không cần tính theo giá trị Yk[n-1] 
trước đó. 
Do        
2
1
k
j
N
kX k Y n S n e S n
−
= = − − nên để tính X[k] chỉ cần thực hiện phép nhân 
với 
2 k
j
Ne
−
 một lần duy nhất, khác với (32) là phải thực hiện phép nhân với số phức 
2 k
j
Ne
−
với N lần, vì vậy giảm các bước tính toán cho vi xử lý, tăng tốc độ tính toán cho hệ thống. 
So sánh về khối lượng cần tính toán giữa FFT và Goertzel thể hiện ở bảng 1 [9]. 
Transport and Communications Science Journal, Vol 72, Issue 2 (02/2021), 143-157 
151 
Bảng 1. Bảng so sánh số phép tính giữa phương pháp FFT và Goertzel. 
Phương 
pháp 
Số phép tính 
nhân số thực 
Số phép tính 
cộng số thực 
Số phép tính 
lượng giác 
FFT 4N2 4N2 2N2 
Goertzel 2N2+2N 4N2 2N 
Ta thấy khi sử dụng Goertzel số phép tính lượng giác giảm đi đáng kể. 
3. KẾT QUẢ MÔ PHỎNG VÀ THỬ NGHIỆM 
3.1 Kết quả mô phỏng 
Các kịch bản mô phỏng được thực hiện như sau: tính điện áp hiệu dụng, dòng điện hiệu 
dụng, công suất hiệu dụng và hệ số công suất qua tải với các trường hợp điện áp cấp nguồn là 
sóng sin, sóng không sin (có hài bậc cao) với các dạng tải khác nhau (thuần trở, có cảm 
kháng, tải phức hợp gồm cả thuần trở, cảm kháng và tụ điện). 
Tiến hành thực hiện mô phỏng theo lưu đồ gồm 7 bước như sau: 
- Bước 1: Chọn tần số trích mẫu tín hiệu Fs=10Khz, rời rạc tín hiệu điện áp và dòng điện 
đầu vào. 
- Bước 2: Lựa chọn tần số cần phân tích phổ tại các điểm lân cận với tần số điện lưới (hài 
cơ bản) và hài bậc cao của nó. 
- Bước 3: Sử dụng thuật toán (35) (36) phân tích phổ, vẽ đồ thị và xác định phần thực và 
phần ảo của tín hiệu điện áp và dòng điện tại các tần số lựa chọn ở bước 2. 
- Bước 4: Khôi phục tín hiệu điện áp và dòng điện (công thức (12),(15)) ở dạng tín hiệu 
điều hòa tương ứng với các sóng hài khi sử dụng các dữ liệu ở bước 3. 
- Bước 5: Xác định góc lệch pha giữa các tín hiệu điện áp và dòng điện tại các tần số sóng 
hài. 
- Bước 6: Tính điện áp và dòng điện hiệu dụng (công thức (16), (17)) . 
- Bước 7: Tính công suất hiệu dụng của từng sóng hài (công thức (21),(22)) và công suất 
hiệu dụng tổng. 
Sử dụng phần mềm mô phỏng Matlab 2014a thực hiện 2 phương pháp tính công suất: 
Phương pháp 1 theo truyền thống - xác định chu kỳ theo (28) và phương pháp 2 sử dụng thuật 
toán Goertzel (36) để phân tích phổ sóng hài tín hiệu dòng điện và điện áp qua tải và tính 
công suất theo công thức (21), (22). Xét các trường hợp sau: 
- Trường hợp 1: Đưa điện áp sóng sin v(t) 2100sin(2 50t)= vào mạch có cảm kháng 
nhận được dòng điện tải i(t) 225sin(2 50t )
4
= − . 
• Tính toán theo phương pháp 1: 
Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 2 (02/2021), 143-157 
152 
Giá trị hiệu dụng: 2
1
1
( )
=
= 
N
i
V v i
N
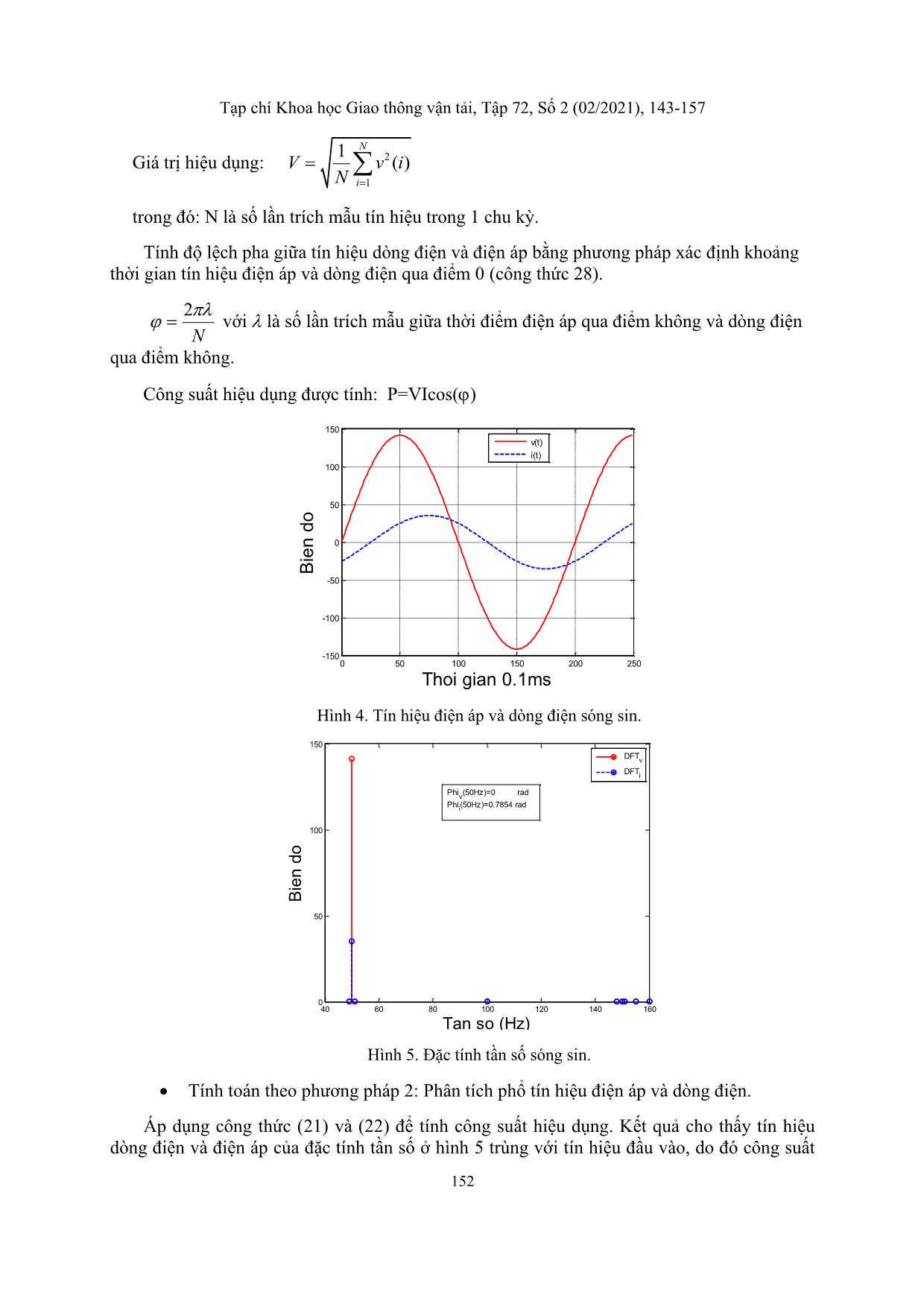
trong đó: N là số lần trích mẫu tín hiệu trong 1 chu kỳ. 
Tính độ lệch pha giữa tín hiệu dòng điện và điện áp bằng phương pháp xác định khoảng 
thời gian tín hiệu điện áp và dòng điện qua điểm 0 (công thức 28). 
2
N
 
 = với  là số lần trích mẫu giữa thời điểm điện áp qua điểm không và dòng điện 
qua điểm không. 
Công suất hiệu dụng được tính: P=VIcos( ) 
0 50 100 150 200 250
-150
-100
-50
0
50
100
150
Thoi gian 0.1ms
B
ie
n
 d
o
v(t)
i(t)
Hình 4. Tín hiệu điện áp và dòng điện sóng sin. 
40 60 80 100 120 140 160
0
50
100
150
Tan so (Hz)
B
ie
n
 d
o
DFT
v
DFT
i
Phi
v
(50Hz)=0 rad
Phi
i
(50Hz)=0.7854 rad
Hình 5. Đặc tính tần số sóng sin. 
• Tính toán theo phương pháp 2: Phân tích phổ tín hiệu điện áp và dòng điện. 
Áp dụng công thức (21) và (22) để tính công suất hiệu dụng. Kết quả cho thấy tín hiệu 
dòng điện và điện áp của đặc tính tần số ở hình 5 trùng với tín hiệu đầu vào, do đó công suất 
Transport and Communications Science Journal, Vol 72, Issue 2 (02/2021), 143-157 
153 
hiệu dụng tính bằng phương pháp 1 và phương pháp 2 bằng nhau (P=1767,8W). Như vậy với 
trường hợp tải thuần trở (góc lệch pha giữa dòng điện và điện áp bằng 0) kết quả của 2 
phương pháp là như nhau. 
- Trường hợp 2: Khi có tác động nhiễu Gauss vào nguồn cấp: 
v(t) 2100sin(2 50t) 2randn(size(t))= + 
Công suất hiệu dụng theo phương pháp 1 là 1762,8W (lệch 0,28% so với khi không có 
nhiễu), trong khi với phương pháp 2 là 1768,2 W (lệch 0,022%). 
- Trường hợp 3: Đưa điện áp sóng không sin cấp cho tải 
 v(t) 2 100sin(2 50t) 25sin(2 150 t)= + 
nhận được dòng điện tải: i(t) 2 25sin(2 50t ) 100sin(2 150t )
2 2
= − + + 
0 50 100 150 200 250
-200
-150
-100
-50
0
50
100
150
200
Thoi gian 0.1ms
B
ie
n
 d
o
v(t)
i(t)
Hình 6. Tín hiệu điện áp và dòng điện không sin. 
40 60 80 100 120 140 160
0
50
100
150
Tan so (Hz)
B
ie
n
 d
o
DFT
v
DFT
i
Hình 7. Phổ tín hiệu sóng không sin. 
Tương tự như trên sử dụng phương pháp 1 tính P= 9466,9W, Vrms=103V, Irms=103A và 
Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 2 (02/2021), 143-157 
154 
θ=0,048 rad và theo phương pháp 2 là P=0 W, Vrms(50hz) =100V, Irms(50Hz)=25A và φ 
(50Hz) =1,5708rad, Vrms(150hz) =24,93V, Irms(50Hz)=100,24A và φ (50Hz) =-1,5708rad. Ở 
đây có sự khác biệt lớn giữa 2 phương pháp, do tải có cả thành phần điện cảm và tụ điện 
(không có điện trở thuần) nên công suất được trả về lưới như vậy phương pháp 2 cho kết quả 
chính xác còn đối với phương pháp 1 do không tính được góc lệch pha giữa dòng điện và điện 
áp đối với từng phổ sóng hài nên kết quả hoàn toàn không đúng. 
 Như vậy phương pháp 1 không thể áp dụng cho trường hợp điện áp không sin với tải 
không phải thuần trở. 
- Trường hợp 4: Khi bổ xung tác động nhiễu Gauss vào nguồn cấp có điện áp không sin. 
0 50 100 150 200 250
-200
-150
-100
-50
0
50
100
150
200
Thoi gian 0.1ms
B
ie
n
 d
o
v(t)
i(t)
Hình 8. Tín hiệu điện áp và dòng điện sóng không sin có nhiễu. 
40 60 80 100 120 140 160
0
50
100
150
Tan so (Hz)
B
ie
n
 d
o
DFT
v
DFT
i
Hình 9. Phổ tín hiệu sóng không sin có nhiễu. 
Phương pháp 1 tính P= 9467W, Vrms=103V, Irms=103A và φ=0,048 rad và theo phương 
pháp 2 là P=4,48 W, Vrms(50hz) =100V, Irms(50Hz)=25A và φ (50Hz) =1,5701rad, 
Vrms(150hz) =24,93V, Irms(50Hz)=100,23A và φ (50Hz) =-1,5707rad. 
Như vậy nhiễu làm sai lệch công suất hiệu dụng là 4,48W. 
Transport and Communications Science Journal, Vol 72, Issue 2 (02/2021), 143-157 
155 
3.2. Kết quả thử nghiệm 
 Cấu trúc bộ thiết bị đo lường và giám sát điện năng trong nghiên cứu này được thể hiện 
trên hình 10. Chức năng của các khối trong hình 10 như sau: 
- Khối thiết bị đo điện áp: có nhiệm vụ đo giá trị tức thời, rời rạc hóa điện áp xoay chiều. 
- Khối thiết bị đo dòng điện: có nhiệm vụ đo giá trị tức thời, rời rạc hóa dòng điện xoay 
chiều. 
- Mạch bắt điểm 0: Đo góc lệch pha giữa điện áp và dòng điện trên tải, từ đó tính ra hệ số 
công suất cos . 
- Khối Tính toán: nhận tín hiệu từ các thiết bị đo điện áp, dòng điện, góc lệnh pha giữa 
điện áp và dòng điện sau đó tính toán giá trị công suất tiêu thụ, cuối cùng là truyền dữ liệu với 
Khối điều khiển và truyền thông. Thuật toán Goertzel được cài đặt và tính toán cho vi xử lý 
STM32F103C8T6. 
- Khối điều khiển và truyền thông: là khối kết nối giữa các thiết bị đo và tính toán với 
thiết bị Smartphone thông qua WiFi, đồng thời khối này cũng làm nhiệm vụ ra lệnh đóng/ngắt 
các thiết bị tiêu thụ điện. 
- Khối cơ sở dữ liệu: truyền nhận và lưu dữ liệu của hệ thống trên cloud đồng thời đóng 
vai trò trung gian để kết nối giữa thiết bị giám sát (Smartphone) với thiết bị điều khiển. 
- Khối thiết bị đóng cắt: đóng cắt dòng điện cung cấp cho Thiết bị tiêu thụ điện. 
- Thiết bị tiêu thụ điện: gồm các thiết bị dân dụng như đèn chiếu sáng, quạt, 
Hình 10. Sơ đồ cấu trúc bộ thiết bị đo lường công suất. 
Để đánh giá thời gian thực hiện thuật toán Goertzel trên Chip vi xử lý STM32F103C8T6 
ta căn cứ vào bảng 1. Với tốc độ xử lý 50 MIPS thời gian tính lệnh nhân và lệnh cộng là 
0,02µs và hàm lượng giác (cos) là 20 µs. Chọn số lần trích mẫu N=200, từ bảng 1 với phương 
pháp FFT cần thời gian 1,6s còn với thuật toán Goertzel cần thời gian xấp sỉ là 12ms. 
Khối Tính 
toán 
Thiết bị 
đo điện áp 
Thiết bị 
đo 
dòng điện 
Mạch bắt 
điểm 0 
Điều 
khiển và 
truyền 
thông 
Cơ sở dữ 
liệu 
Smartphone 
Thiết bị 
đóng cắt 
Thiết bị tiêu 
thụ điện 
u(t) 
i(t) 
Tạp chí Khoa học Giao thông vận tải, Tập 72, Số 2 (02/2021), 143-157 
156 
Một số hình ảnh thử nghiệm bộ thiết bị đo điện năng tiêu thụ được thể hiện trên hình 11. 
a) b) 
Hình 11. a) Bộ thiết bị đo điện năng; b) Kết hợp Bộ thiết bị đo điện năng và thiết bị đa năng PM 
– 2100 của hãng Schneider (Pháp). 
Bảng 2. Bảng so sánh giá trị công suất đo được giữa thiết bị đo điện năng và thiết bị thương mại PM-
2100. 
Loại tải Lần đo 
Công suất đo 
được bằng thiết 
bị PM-2100 (KW) 
Công suất đo 
được bằng thiết bị 
đo điện năng 
(KW) 
Độ chênh lệch 
giữa 2 thiết bị đo 
(KW) 
Bóng đèn sợi 
đốt 200W 
1 0,1230 0,1248 0,0018 
2 0,1230 0,1238 0,0008 
3 0,1230 0,1245 0,0015 
Quạt cây 
45W 
1 0,0350 0,0359 0,0009 
2 0,0350 0,0351 0,0001 
3 0,0350 0,0348 0,0002 
Ấm đun 
nước siêu 
tốc 1500W 
1 1,4930 1,5034 0,0104 
2 1,4930 1,5059 0,0129 
3 1,4930 1,5074 0,0114 
Tải tổng hợp 
1 1,6330 1,6789 0,0459 
2 1,6330 1,6795 0,0465 
3 1,6330 1,6782 0,0452 
Từ bảng 2 nhận thấy: So với thiết bị PM – 2100 đã được thương mại hóa của hãng 
Schneider (Pháp) thì thiết bị được chế tạo có sai số đo lớn nhất là 2,85% (tương ứng với tải 
tổng hợp), giá trị sai số này nằm trong giới hạn chấp nhận được của Tiêu chuẩn đo lường quốc 
gia là dưới 5%. 
4. KẾT LUẬN 
Việc tính toán công suất hiệu dụng và năng lượng tiêu thụ với hệ thống điện có sóng hài 
bậc cao cần phân tích phổ tín hiệu, nếu sử dụng biến đổi Fourier nhanh FFT cần khối lượng 
tín toán lớn trên vi xử lý không đảm bảo thời gian thực trên các thiết bị có giá thành thấp. Với 
STM32F103C8T6 
Smartphone 
Transport and Communications Science Journal, Vol 72, Issue 2 (02/2021), 143-157 
157 
hệ thống điện lưới, giá trị biến động của tần số nằm trong phạm vi lân cận tần số cơ bản 
(50Hz, và hài bậc cao của 50Hz) nên thay bằng việc sử dụng FFT để xác định phổ trên toàn 
dải chỉ cần xác định đặc tính tần số ở các điểm lân cận này. 
Trong trường hợp này sử dụng thuật toán Goertzel cho phép giảm khối lượng tính toán 
(công thức 35, 36). Các kết quả mô phỏng và thử nghiệm trên thiết bị thực cho thấy đảm bảo 
độ chính xác của kết quả đo với các dạng điện áp khác nhau cũng như tải khác nhau. 
Các nghiên cứu tiếp theo hướng tới bài toán đo công suất của hệ thống điện lưới 3 pha. 
 LỜI CẢM ƠN 
Nghiên cứu này được tài trợ bởi Trường đại học Giao thông vận tải trong đề tài mã số T2020-
DT-005. 
TÀI LIỆU THAM KHẢO 
[1]. Analog Device Enering IC with Autocalibration ADE915A, Technical Support 2018. 
[2]. K. Gandhi, H. O. Bansal, Smart Metering in Electric Power Distribution System, Internaltional 
Conference on Control, Automation, Robotics and Embedded System, 2013. 
[3]. Y. Chen, J. Lan, Implementation of Power Measurement System with Fourier Series and Zero-
Crossing Algorithm, International Symposium on Computer, Consumer and Control, 2014. 
[4]. L.S. Czarnecki, Budeanu and Fryze: Two frameworks for interpreting power properties of circuits 
with nonsinusoidal voltages and currents, Electrical Engineering, 80 (1997) 359-367. 
https://doi.org/10.1007/BF01232925 
[5]. Texas Instrument, Modified Goertzel Algorith in DTMF Detection Using the TMS320C80, Digital 
Signal Processing Solutions, 1996. 
[6]. C. Sidney Burrus, Fast Fourier Transforms. Textbook of LibreTexts libraries, Rice University, 
2020. 
[7]. M. Kekelj, N. Bulic, V. Sucic, An FPGA Implementation of the Goertzel Algorithm in a Non-
Destructive Eddy Current Testing, International Conference on Signals and Systems, 2017, pp. 180-
184. https://doi.org/10.1109/ICSIGSYS.2017.7967036 
[8]. A. Vitali, The Goertzel algorithm to compute individual terms of the discrete Fourier transform 
(DFT), Design tip DT 0089, ST Microelectronics 2017. 
[9]. S. Nuccio, A. Catalliotti, IEEE Standard: Definitions for the Measurement of Electric Power 
Quantities Under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions, IEEE Std 1459-
2010, February 2010. 
[10]. J. L. Willems, The IEEE standard 1459: What and why?, IEEE International Workshop on 
Applied Measurements for Power Systems, 2010.