Hybrid active power filter method in frequency domain for quality improvement in variable frequency drive applications

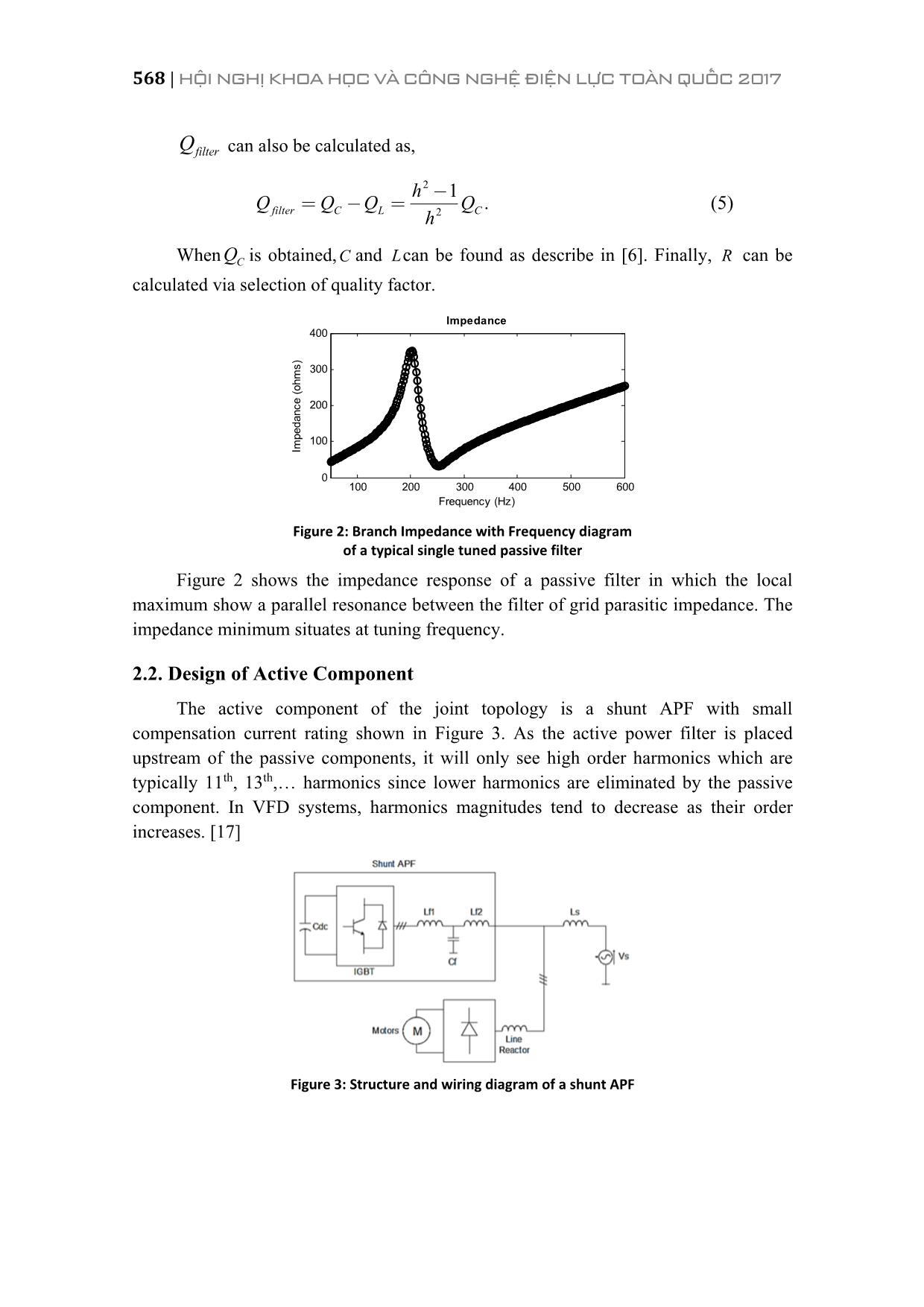
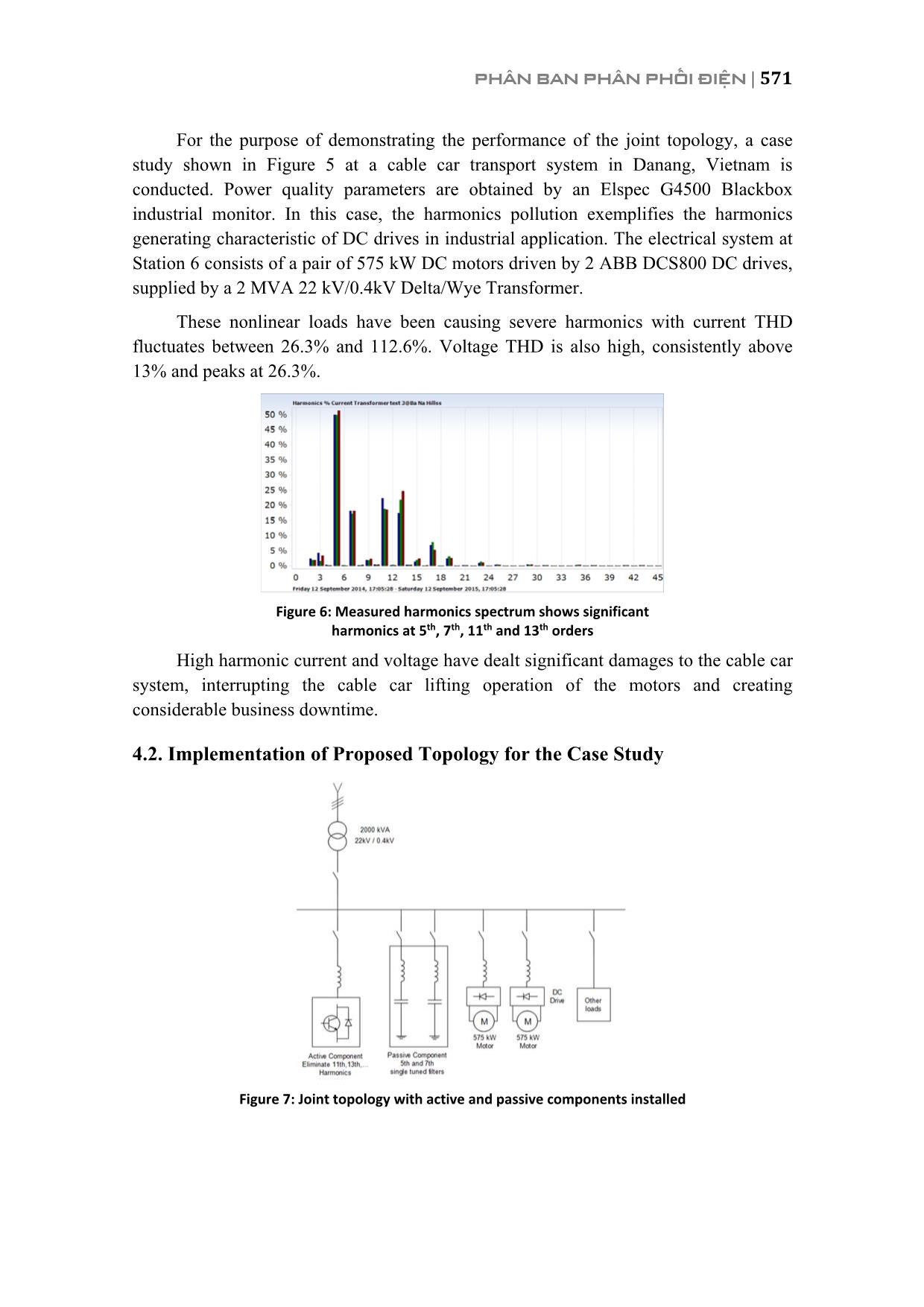
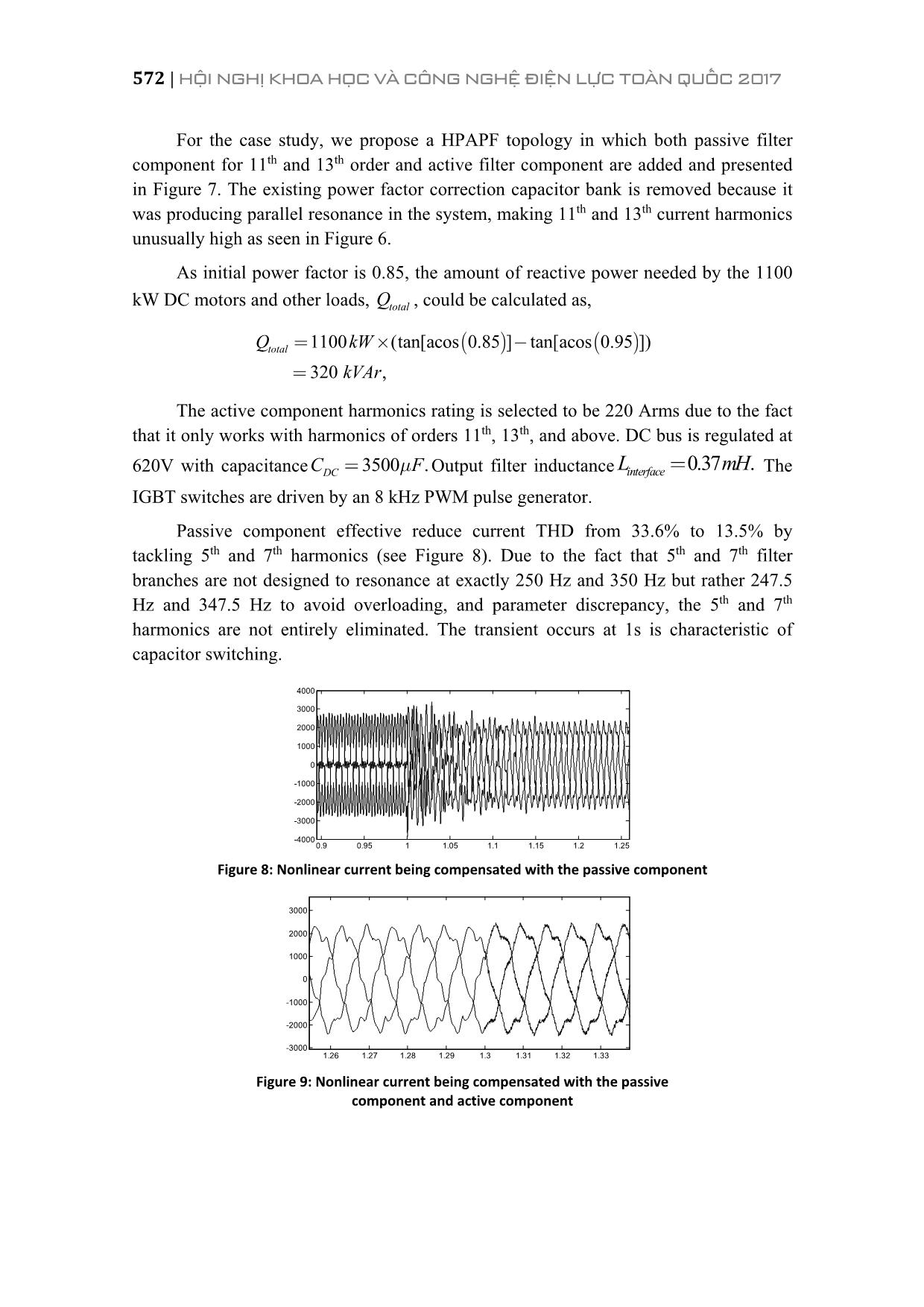
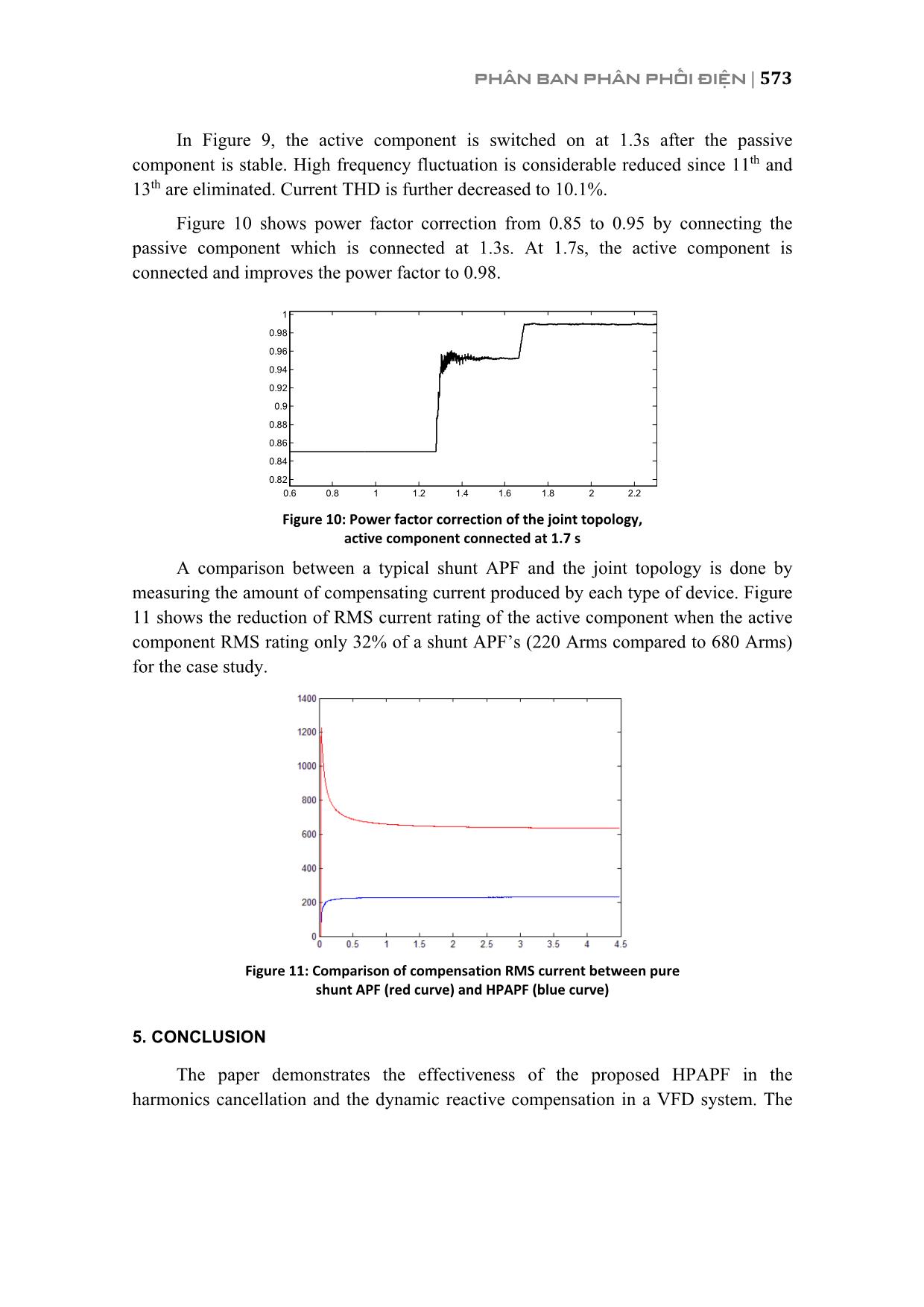
e phase power networks is proposed 
and studied. The strategy is a parallel configuration of low order passive harmonics 
filter and selective shunt active power filter. Frequency domain Fourier Transform 
analysis and robust PI controllers are used to design control algorithm. PHPF 
performance is verified by modeling and using Matlab/Simulink software for the 
simulations. 
2. CONSTRUCTION OF PROPOSED HPAPF 
2.1. Design of Passive Components 
Single tuned topology is chosen to implement the passive component because it is 
simple to construct and economically viable. Along with high pass and double tuned 
filters, single tuned passive filter is one of the most commonly used type of harmonics 
filter in three phase systems. 
PHÂN BAN PHÂN PHỐI ĐIỆN | 567 
Figure 1: Single tuned passive filter diagram 
The passive components of the joint topology are designed to eliminate the 
majority of the lower part of the harmonic spectrum, typically 5th and/or 7th harmonics. 
The quality factor of the filter Q is typically chosen in the range of 15 to 80 and 
inversely proportional to the branch resistance. 
Filter tuning frequency hf and tuning angular frequency hw are calculated as, 
1 1, . (1)
2h h
f
LC LC
wp= = 
The relationship between filter inductance L and capacitance C is presented as, 
 , , 2
50
1 , (2)
( )L h C h Hz
Z Z L
h Cw= = 
where ,L hZ and C,hZ are filter inductor and capacitor impedance at hf , h is the harmonic 
order of the passive branch, 50Hzw is the angular frequency at fundamental frequency. 
Filter quality factor Q is calculated as, 
1 , (3)L LQ
R R C
Z= = 
Where LZ is inductor impedance at fundamental frequency. 
As seen in Figure 1, two PHF branches are tuned at 5th 1 1 1( , , )f f fL C R and 7th 
2 2 2( , , ).f f fL C R Along with harmonics filtering functionality, the two passive branches 
also provide background reactive power compensation for power factor correction. 
For power factor correction from an initial initialPF to a desired finalPF value, the 
amount of reactive power produced by the passive component filterQ is calculated as 
follow: 
 ( ) ( )(tan[acos ] tan[acos ]) (4)inifilter lo tiad finalalQ P PF PF= - 
568 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
filterQ can also be calculated as, 
2
2 . (5)
1
filter C L C
hQ Q Q Q
h
-= - = 
When CQ is obtained,C and Lcan be found as describe in [6]. Finally, R can be 
calculated via selection of quality factor. 
Figure 2: Branch Impedance with Frequency diagram 
of a typical single tuned passive filter 
Figure 2 shows the impedance response of a passive filter in which the local 
maximum show a parallel resonance between the filter of grid parasitic impedance. The 
impedance minimum situates at tuning frequency. 
2.2. Design of Active Component 
The active component of the joint topology is a shunt APF with small 
compensation current rating shown in Figure 3. As the active power filter is placed 
upstream of the passive components, it will only see high order harmonics which are 
typically 11th, 13th, harmonics since lower harmonics are eliminated by the passive 
component. In VFD systems, harmonics magnitudes tend to decrease as their order 
increases. [17] 
Figure 3: Structure and wiring diagram of a shunt APF 
100 200 300 400 500 600
0
100
200
300
400
Impedance
Im
pe
da
nc
e 
(o
hm
s)
Frequency (Hz)
PHÂN BAN PHÂN PHỐI ĐIỆN | 569 
In principle, the active filter stores electrical energy in its DC bus, which is a high 
voltage DC capacitor, and convert this DC voltage into three phase AC voltage and 
current. The control algorithm decides how much reactive power is being supplied to 
the grid by varying the output current phase and amplitude. This can be achieved to 
estimating the correct amount of reactive power needed by the non linear load using 
voltage and current feedback signals measured at the point of common coupling (PCC) 
and DC bus. Details about the control algorithm will be discussed further in the next 
section. 
3. CONTROL METHODOLOGY 
3.1. Frequency Domain Analysis of Harmonics Current 
Fourier Transform is used to analyse load feedback signal to provide flexible 
selective harmonic current generation. 
Discrete Fourier Transform (DFT) is the digital form of Fourier Transform. DFT 
of a discrete signal sampled N times in a cycle is defined: 
21
1
0
 (. 6)
j kN
n
k
k
X x e
p-
=
=å 
Inverse DFT of 1X is defined as: 
2
1 1
1 (7).
j k
N
kx X eN
p-= 
This allows the selection of high order harmonics while omitting lower 
components. According to Fourier Transform, load current can be represented as: 
( ) ( )1 ,
2
( ), (8)load load load n
n
i t i t i t
¥
=
= +å 
where, 1( )load ti represents the fundamental component and , ( )load ni t is the function of 
harmonic components. 
3.2. APF Reference Current Calculation and Control Loops For PWM 
Generation 
Figure 4 is presented to illustrate the control algorithm for the active component. 
Assuming sampling rate is 12800 Hz, which is 256 samples/electrical cycle. The 
amount of frequency bin obtained by DFT is 256 bins representing 128 frequency 
components of load current. Reference current is computed by extract high order 
570 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
harmonics from DFT analysis of load feedback current, namely 11th to 128th frequency 
bins, and then takes the inverse DFT of this frequency range. 
Figure 4: Control algorithm for the active component 
A control loop also includes a DC bus voltage regulator in order to keep DC bus 
stable at a reference value. Output of the DC bus PI controller is then added to 
harmonics reference current along with reactive power compensation reference current. 
Another PI controller is used to generate pulse width modulation signals and regulate 
APF output compensation current. The PWM generation module is a Sinusoidal PWM 
which creates PWM pulses a specific switching frequency, normally from 8 kHz to 15 
kHz. 
4. SIMULATION RESULTS 
4.1. Case Study of a VFD System 
Figure 5: Basic electrical diagram of the cable car transport 
system using DC drives – Danang, Vietnam 
PHÂN BAN PHÂN PHỐI ĐIỆN | 571 
For the purpose of demonstrating the performance of the joint topology, a case 
study shown in Figure 5 at a cable car transport system in Danang, Vietnam is 
conducted. Power quality parameters are obtained by an Elspec G4500 Blackbox 
industrial monitor. In this case, the harmonics pollution exemplifies the harmonics 
generating characteristic of DC drives in industrial application. The electrical system at 
Station 6 consists of a pair of 575 kW DC motors driven by 2 ABB DCS800 DC drives, 
supplied by a 2 MVA 22 kV/0.4kV Delta/Wye Transformer. 
These nonlinear loads have been causing severe harmonics with current THD 
fluctuates between 26.3% and 112.6%. Voltage THD is also high, consistently above 
13% and peaks at 26.3%. 
Figure 6: Measured harmonics spectrum shows significant 
harmonics at 5th, 7th, 11th and 13th orders 
High harmonic current and voltage have dealt significant damages to the cable car 
system, interrupting the cable car lifting operation of the motors and creating 
considerable business downtime. 
4.2. Implementation of Proposed Topology for the Case Study 
Figure 7: Joint topology with active and passive components installed 
572 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
For the case study, we propose a HPAPF topology in which both passive filter 
component for 11th and 13th order and active filter component are added and presented 
in Figure 7. The existing power factor correction capacitor bank is removed because it 
was producing parallel resonance in the system, making 11th and 13th current harmonics 
unusually high as seen in Figure 6. 
As initial power factor is 0.85, the amount of reactive power needed by the 1100 
kW DC motors and other loads, totalQ , could be calculated as, 
( ) ( )1100 (tan[acos 0.85 ] tan[acos 0.95 ])
320 ,
totalQ kW
kVAr
= ´ -
= 
The active component harmonics rating is selected to be 220 Arms due to the fact 
that it only works with harmonics of orders 11th, 13th, and above. DC bus is regulated at 
620V with capacitance 3500 .DCC Fm= Output filter inductance 0.37 .interfaceL mH= The 
IGBT switches are driven by an 8 kHz PWM pulse generator. 
Passive component effective reduce current THD from 33.6% to 13.5% by 
tackling 5th and 7th harmonics (see Figure 8). Due to the fact that 5th and 7th filter 
branches are not designed to resonance at exactly 250 Hz and 350 Hz but rather 247.5 
Hz and 347.5 Hz to avoid overloading, and parameter discrepancy, the 5th and 7th 
harmonics are not entirely eliminated. The transient occurs at 1s is characteristic of 
capacitor switching. 
Figure 8: Nonlinear current being compensated with the passive component 
Figure 9: Nonlinear current being compensated with the passive 
component and active component 
0.9 0.95 1 1.05 1.1 1.15 1.2 1.25
-4000
-3000
-2000
-1000
0
1000
2000
3000
4000
1.26 1.27 1.28 1.29 1.3 1.31 1.32 1.33
-3000
-2000
-1000
0
1000
2000
3000
PHÂN BAN PHÂN PHỐI ĐIỆN | 573 
In Figure 9, the active component is switched on at 1.3s after the passive 
component is stable. High frequency fluctuation is considerable reduced since 11th and 
13th are eliminated. Current THD is further decreased to 10.1%. 
Figure 10 shows power factor correction from 0.85 to 0.95 by connecting the 
passive component which is connected at 1.3s. At 1.7s, the active component is 
connected and improves the power factor to 0.98. 
Figure 10: Power factor correction of the joint topology, 
active component connected at 1.7 s 
A comparison between a typical shunt APF and the joint topology is done by 
measuring the amount of compensating current produced by each type of device. Figure 
11 shows the reduction of RMS current rating of the active component when the active 
component RMS rating only 32% of a shunt APF’s (220 Arms compared to 680 Arms) 
for the case study. 
Figure 11: Comparison of compensation RMS current between pure 
shunt APF (red curve) and HPAPF (blue curve) 
5. CONCLUSION 
The paper demonstrates the effectiveness of the proposed HPAPF in the 
harmonics cancellation and the dynamic reactive compensation in a VFD system. The 
0.6 0.8 1 1.2 1.4 1.6 1.8 2 2.2
0.82
0.84
0.86
0.88
0.9
0.92
0.94
0.96
0.98
1
574 | HỘI NGHỊ KHOA HỌC VÀ CÔNG NGHỆ ĐIỆN LỰC TOÀN QUỐC 2017 
obtained results show that the active component RMS current rating in the HPAPF 
system is only 32% of the traditional active power filter rating with the same harmonics 
filtering performance. This reduction in rating implies a great economic advantage of 
the proposed HPAPF compared to the traditional APFs. Moreover, the proposed 
HPAPF shows significant potential in installation footprint reduction, which is 
important in space constraint sites such cruise ships, oil rigs, since VFDs are common 
at these places. 
Future works involves thermal design for the active component and a detailed 
transient analysis of HPAPF systems. Furthermore, an electrical prototype will also be 
developed to real world settings. 
REFERENCES 
[1] Akagi, H. 2006. Modern active filters and traditional passive filters. Bulletin of the Polish 
Academy of SciencesTechnical Sciences. 54(3). 
[2] Nguyen, K.A. and Bui, Q.K. 2009. An active filters design for the reduction of current 
harmonic and the compensation of reactive power for induction melting furnace power. 
Journal of science & Technology, the University of Danang. 4(33): 35 42. 
[3] Yasir, M., Kazemi, S., Lehtonen, M. and Fotuhi Firuzabad, M. 2012. Optimal selection of 
voltage sag mitigation solution based on event tree method. Proc. on Electric Power 
Quality and Supply Reliability Conference (PQ).1 6. 
[4] Grady, W. M., Samotyj, M. J. and Noyola, A. H. 1992. The application of network objective 
functions for actively minimizing the impact of voltage harmonics in power systems. IEEE 
Transactions on Power Delivery. 7(3): 1379 1386. 
[5] Godbole, P. 2014. Effect of harmonics on active power flow and apparent power in the 
power system. IOSR Journal of Electronics and Communication Engineering (IOSR JECE): 
39 43. 
[6] Singh, B., Al Haddad, K. and Chandra, A. 1999. A Review of Active Filters for Power 
Quality Improvement. IEEE Transactions On Industrial Electronics. 46(5). 
[7] Tupsa ard, J., Chamchoy, C. and Tayjasanant, T. 2011. High voltage passive harmonic filter 
design. Proc. on Electrical Engineering/Electronics, Computer, Telecommunications and 
Information Technology (ECTI CON) International Conference. 804 807. 
[8] Das, J. C. 2003. Passive filters potentialities and limitations. Proc. on Pulp and Paper 
Industry Technical Conference, Conference Record of the 2003 Annual, IEEE.187 197. 
[9] Tang, Y., et al. 2012. Generalized design of high performance shunt active power filter 
with output LCL filter. IEEE Transactions on Industrial Electronics 59(3):1443 1452. 
PHÂN BAN PHÂN PHỐI ĐIỆN | 575 
[10] Akagi, H., Akira N. and Satoshi A. 1986. Control strategy of active power filters using 
multiple voltage source PWM converters. IEEE Transactions on Industry Applications. 
3:460 465. 
[11] Bhavaraju, V. B. and Prasad, N. E. 1993. Analysis and design of an active power filter for 
balancing unbalanced loads. IEEE Transactions on Power Electronics. 8(4): 640 647. 
[12] Demirdelen, T., et al. 2013. Review of hybrid active power filter topologies and 
controllers. Proc. of Fourth International Conference on Power Engineering, Energy and 
Electrical Drives (POWERENG), IEEE. 
[13] Kim, S. and Prasad N. E. 2002. A new hybrid active power filter (APF) topology. IEEE 
Transactions on Power Electronics. 17(1): 48 54. 
[14] Luo, A. et al. 2009. Development of hybrid active power filter based on the adaptive fuzzy 
dividing frequency control method. IEEE Transactions on Power Delivery. 24(1): 424 432. 
[15] Tzung Lin, L., Yen Ching, W., Jian Cheng, L. and Guerrero, J.M. 2015. Hybrid Active Filter 
With Variable Conductance for Harmonic Resonance Suppression in Industrial Power 
Systems. IEEE Transactions on Industrial Electronics. 62(2):746 756. 
[16] Susila, D.J. and Rajathy, R. 2013. Power Quality Enhancement Using Hybrid Active Filter. 
International Journal of Engineering Science and Innovative Technology (IJESIT). 2(3). 
[17] Asadi, M. and Jalilian, A.R. 2012. A Hybrid Active Power Filter Comprising an Active 
Electromagnetic Filter. PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 
0033 2097. R. 88 NR 10a. 
[18] Peeran, S.M., and Creg, W.P.C 1995. Application, design, and specification of harmonic 
filters for variable frequency drives. IEEE Transactions on Industry Applications. 31(4): 
841 847.