Giáo trình Tín hiệu và hệ thống (Phần 2)
5.1 CƠ BẢN VỀ ĐIỀU CHẾ TÍN HIỆU
Điều chế (Modulation) là quá trình ánh xạ tin tức vào sóng mang bằng cách thay
đổi thông số của sóng mang (biên độ, tần số hay pha) theo tin tức.
Điều chế đóng vai trò rất quan trọng, không thể thiếu trong hệ thống thông tin.
5.1.1 Vị trí của điều chế trong hệ thống thông tin
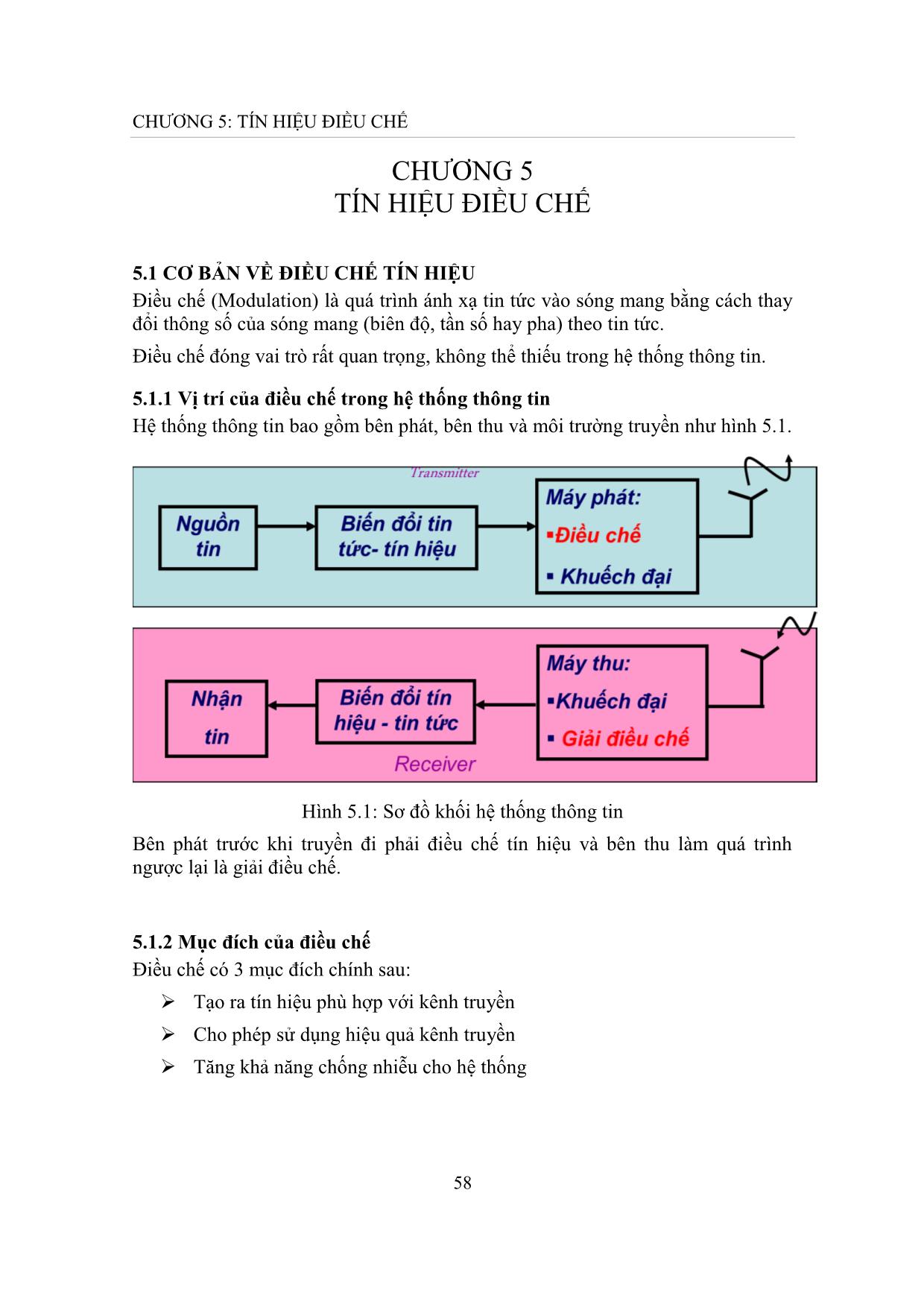
Hệ thống thông tin bao gồm bên phát, bên thu và môi trường truyền như hình 5.1.
Hình 5.1: Sơ đồ khối hệ thống thông tin
Bên phát trước khi truyền đi phải điều chế tín hiệu và bên thu làm quá trình
ngược lại là giải điều chế.
5.1.2 Mục đích của điều chế
Điều chế có 3 mục đích chính sau:
Tạo ra tín hiệu phù hợp với kênh truyền
Cho phép sử dụng hiệu quả kênh truyền
Tăng khả năng chống nhiễu cho hệ thốngCHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ
59
5.1.3 Phân loại các phương pháp điều chế
Dựa vào kỹ thuật điều chế (thay đổi thông số của song mang) hoặc dạng tín hiệu
ngõ vào, điều chế được phân loại thành các phương pháp như hình 5.2.
Trang 1

Trang 2
Trang 3
Trang 4
Trang 5

Trang 6
Trang 7

Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Giáo trình Tín hiệu và hệ thống (Phần 2)

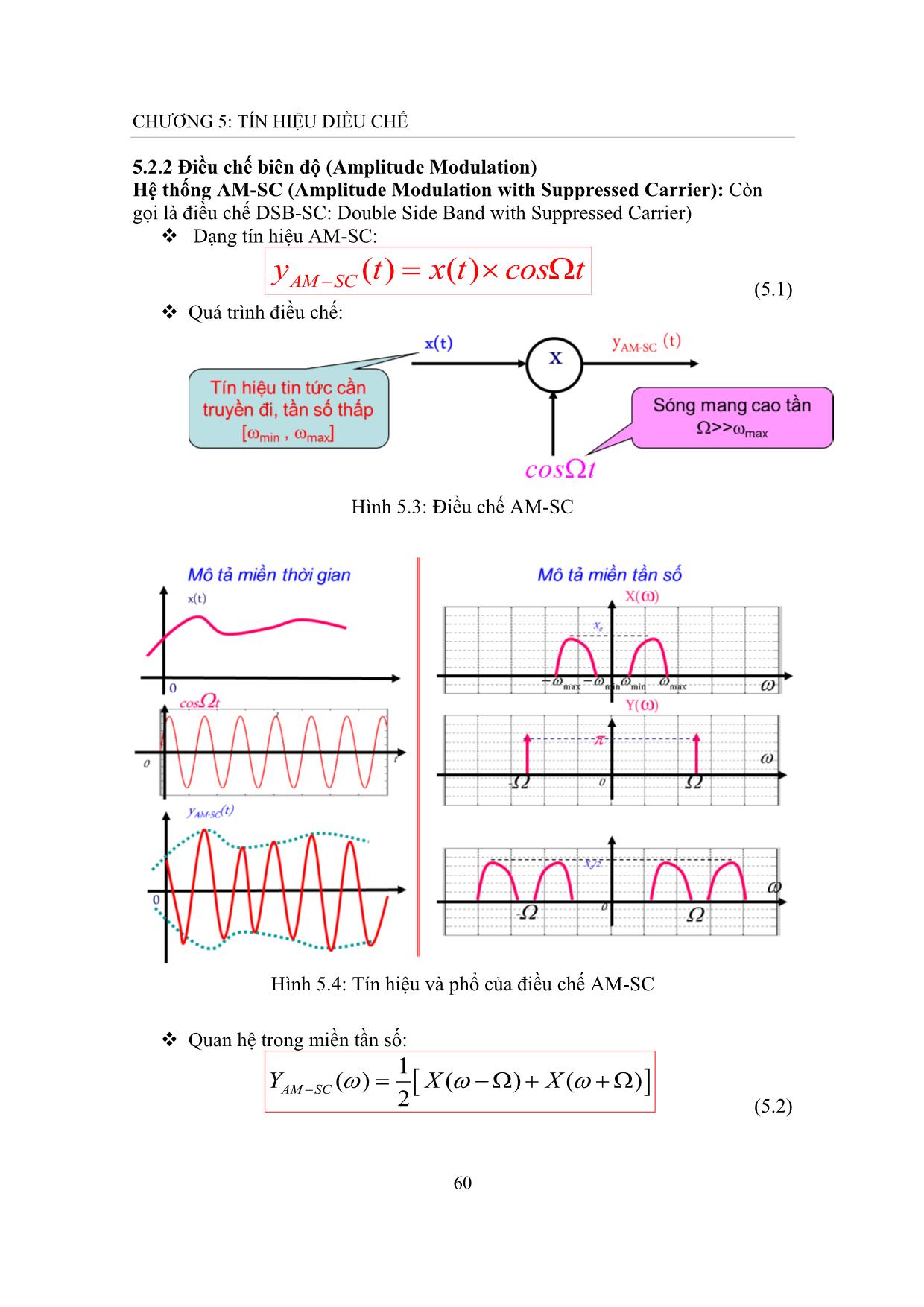
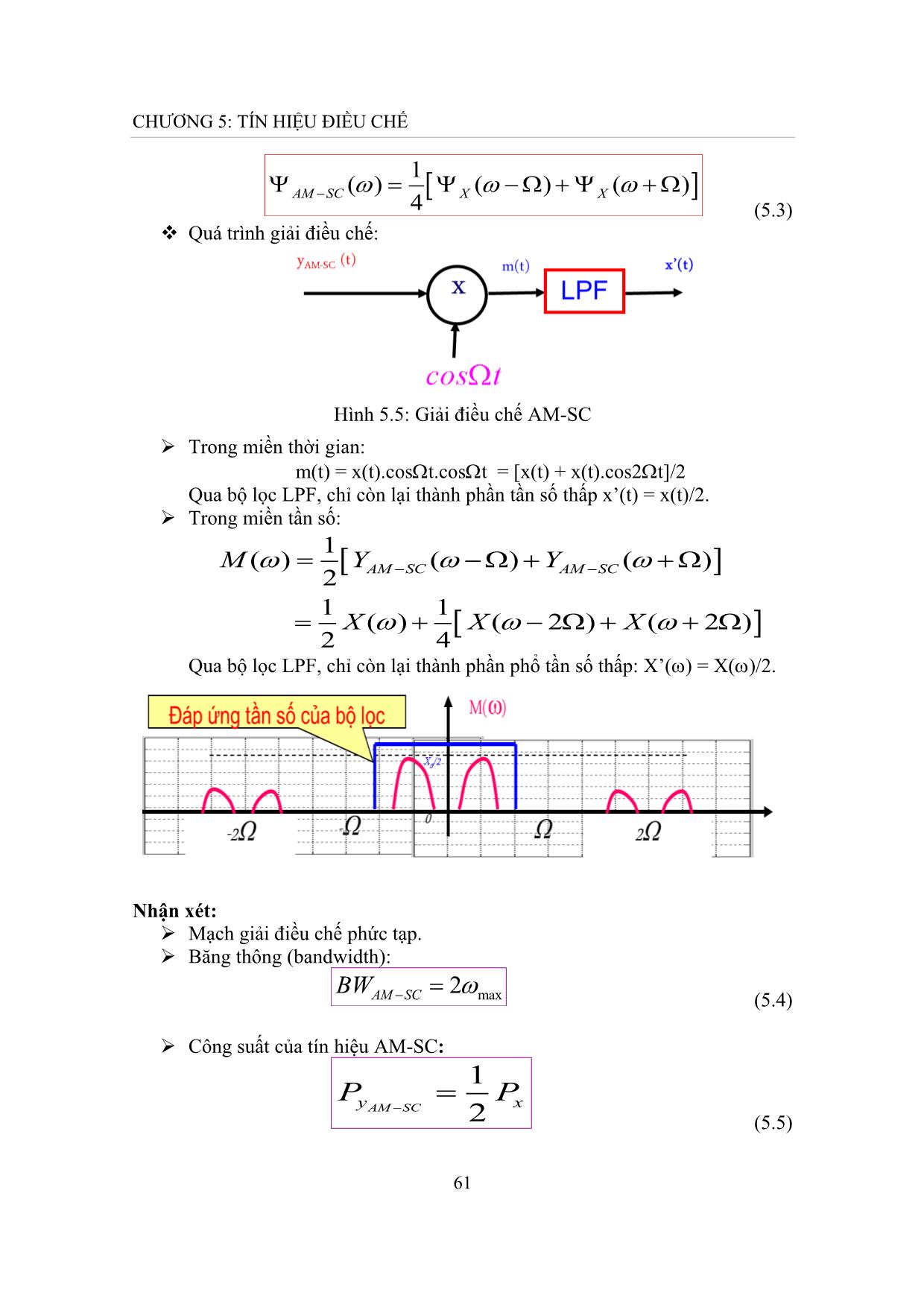
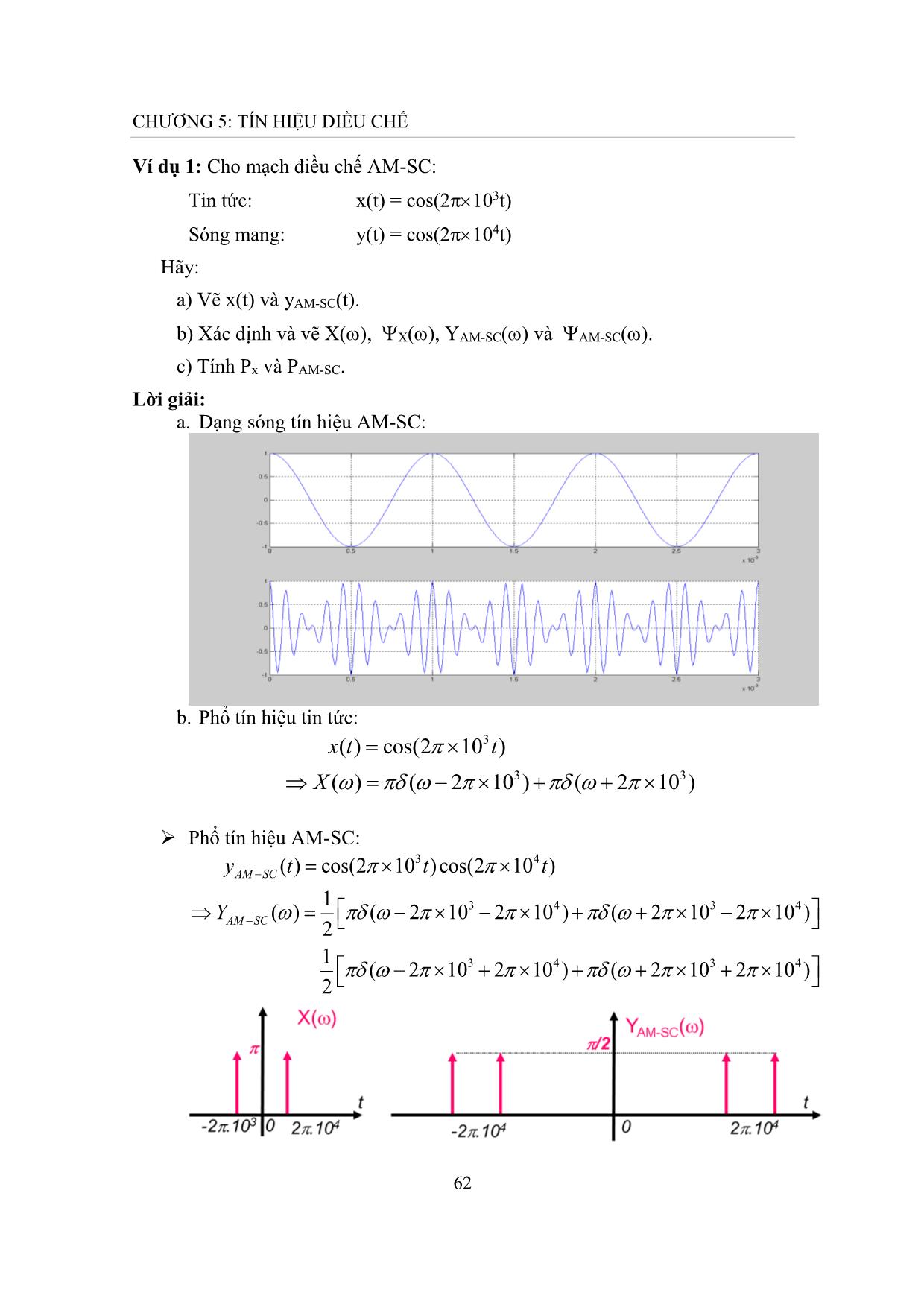
ệu PAM rộng vô hạn, nhưng phần lớn công suất tập trung trong khoảng (-2 /, 2 /). Vì phổ của PAM tập trung xung quanh tần số thấp, nên muốn truyền đi cần điều chế lần nữa (ví dụ PAM-AM, PAM-FM, vv) Ví dụ 3: Cho hệ thống PAM như sau: 76 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ 2 x();; t Sa t 01T H() 2 0 Hãy: a. Xác định và vẽ Z() khi 1=3 0; 1=1.5 0 b. Xác định v(t) và tính Ev trong hai trường hợp 1=3 0; 1=1.5 0. Lời giải: a. Do z(t) là tín hiệu PAM lý tưởng, nên phổ có dạng sau: 12 YPAM ( ) X ( n 11 ); TTn Trong đó: x()()() t Sa0 t X 00 2 1 n Z() 1 T 2 n 00 b. Xác định tín hiệu ngõ ra: 77 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ VZH()()() 1 *1 3 0 :V ( ) v ( t ) Sa 0 t 00TT 2 2 *10 1.5 :V ( ) 0TT 2 0 0 0 210t v() t Sa0 t Sa TT22 c. Tính năng lượng tín hiệu ngõ ra: 2 11 0 * 3 :E | V ( ) |2 d d 10v 2 2 0 00TT 22 1 00/2 2 5 * 1.5 :E d d 10v 2 0 0TTT /2 0 2 0 0 5.3.3 Các hệ thống điều chế xung khác Điều chế độ rộng xung PDM (Pulse Duration Modulation) Điều chế vị trí xung PPM (Pulse Position Modulation) 78 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ Vị trí của điều chế PAM trong hệ thống thông tin: Điều chế PAM có vị trí trong hệ thống thông tin được thể hiện như trong hình 5.14. Hình 5.14: Vị trí điều chế PAM trong hệ thống thông tin 79 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ BÀI TẬP CHƯƠNG 5 Câu 1: Cho mạch điều chế AM-SC: Tin tức: x(t) = 2cos(2 10t) Sóng mang: y(t) = cos(2 103t) Hãy: a) Vẽ x(t) và yAM-SC(t) ? b) Xác định và vẽ X(), X(), YAM-SC() và AM-SC() ? c) Tính Px và PAM-SC? 3 Câu 2: Cho mạch điều chế AM: yAM(t) = [A+x(t)]cos(2 10 t) Biết tin tức: x(t) = 2cos(2 10t) và A = 4 Hãy: a) Vẽ x(t) và yAM(t) ? b) Xác định và vẽ X(), X(), YAM () và AM() ? c) Tính Px và PAM? 5 Câu 3: Cho mạch điều chế AM: yAM(t) = [A+x(t)]cos(2 10 t) x(t) A -2T -T 0 T/2 T 2T t -A Hãy: a) Vẽ yAM(t) khi A=2, T=4. b) Xác định phổ X(), YAM(). c) Tính Px và PAM. d) Xác định giá trị của A để tách sóng không bị méo trong mạch tách sóng hình bao. Câu 4: Cho hệ thống PAM như sau: 80 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ 2 x();; t Sa t 01T H() 2 0 Hãy: a) Xác định và vẽ Z() khi 1=4 0; 1= 0. b) Xác định v(t) và tính Ev trong hai trường hợp 1=4 0; 1= 0. Câu 5: Tín hiệu tin tức x(t) Saw0t , yAM _ SC (t) x(t)cost . Hãy: a) Vẽ dạng sóng điều chế yAM _ SC (t) . b) Xác định hàm mật độ phổ công suất của x(t) , . c) Xác định công suất P , P . x y AM _ SC Câu 6: Một hệ thống thực hiện điều chế PAM như hình vẽ. Biết x(t) X (w) y(t) x(t) Xác định phổ tín hiệu yPAM (t) trong 2 trường hợp: 1 t a) Lí tưởng, tức y(t) ||| T T t 1 t t nT b) Thực tế, tức y(t) Y * ||| Y T T n t 1 t T Câu 7: Cho yPAM (t) x(t)Y ||| , với x(t) Saw1t ; ; T T 4 2w0 và w0 2w1 . a) Tìm và vẽ phổ của ? 81 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ w w w w b) Cho y (t) đi qua mạch lọc K(w) 0 0 , tìm z(t) ở PAM w0 w0 đầu ra mạch lọc? w Câu 8: Đầu vào của mạch lọc thông thấp có đặc tuyến tần số K(w) , wo được đưa đến tín hiệu y AM (t) (1 mcos w1t)cos wot ; cho biết hệ số độ sâu 4 1 điều chế m = 0,5 và w w . Hãy tìm tín hiệu ở đầu ra mạch lọc z(t), phổ Z(w) 1 2 o và công suất của tín hiệu. Câu 9: Cho các tín hiệu x(t) = cos2ot + 2cos4ot và yAM(t) = [3 + x(t)]cos100ω0t. Hãy xác định: a) X() và vẽ phổ của x(t). Tính Px. b) YAM() và vẽ phổ của yAM(t). Tính PAM. Câu 10: Cho x(t) cos 2t 3sin 3t 4cos5t . Xác định: a) Phổ của tín hiệu x(t). b) Hàm mật độ phổ công suất và công suất của tín hiệu x(t). 6 3 Câu 11: Cho yAM (t) 2 x(t)cos10 t , x(t) cos2.10 t a) Xác định YAM (w). b) Cho tín hiệu y AM (t) đi qua mạch lọc có hàm truyền như hình vẽ. Xác định tín hiệu ngõ ra mạch lọc. K(w) 0 w -106-3.103 -106+3.103 106-3.103 106+3.103 -106 106 Câu 12: Cho hệ thống như hình vẽ. x1(t) x (t) y (t) K(w) x2(t) 82 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ 2 j40t Trong đó: x1(t) 4sin 40t, x2 (t) Sa4t,k(t) (Sa 2t)e a) Tìm () , (w) . x1 x1 b) Xác định và vẽ X(w). c) Xác định K(w), Y(w), y(t). 83 CÂU HỎI TRẮC NGHIỆM 1. Tín hiệu năng lượng là tín hiệu: a. có năng lượng hữu hạn b. có công suất hữu hạn c. có năng lượng vô hạn d. có công suất vô hạn 2. Tín hiệu công suất là tín hiệu: a. có năng lượng hữu hạn b. có công suất hữu hạn c. có năng lượng vô hạn d. có công suất vô hạn 3. Tín hiệu tương tự (analog) là tín hiệu: a. có biên độ và thời gian liên tục b. có biên độ rời rạc và thời gian liên tục c. có biên độ liên tục và thời gian rời rạc d. có biên độ rời rạc và thời gian rời rạc 4. Tín hiệu lượng tử là tín hiệu: a. có biên độ và thời gian liên tục b. có biên độ rời rạc và thời gian liên tục c. có biên độ liên tục và thời gian rời rạc d. có biên độ rời rạc và thời gian rời rạc 5. Tín hiệu rời rạc là tín hiệu: a. có biên độ và thời gian liên tục b. có biên độ rời rạc và thời gian liên tục c. có biên độ liên tục và thời gian rời rạc d. có biên độ rời rạc và thời gian rời rạc 6. Tín hiệu số (digital) là tín hiệu: a. có biên độ và thời gian liên tục b. có biên độ rời rạc và thời gian liên tục c. có biên độ liên tục và thời gian rời rạc d. có biên độ rời rạc và thời gian rời rạc 7. Khái niệm tín hiệu là: a. Sự biểu hiện vật lý của tin tức mà nó mang từ nguồn tin đến nơi nhận tin b. Nội dung mà tín hiệu thể hiện c. Một dạng tín hiệu mà nơi nhận tin không cần quan tâm d. Tất cả a, b, c đều sai 8. Khái niệm thông tin là: a. Sự biểu hiện vật lý của tin tức mà nó mang từ nguồn tin đến nơi nhận tin b. Nội dung mà tín hiệu thể hiện c. Một dạng tín hiệu mà nơi nhận tin không cần quan tâm d. Tất cả a, b, c đều sai 9. Phân tích phổ là phương pháp phân tích: a. Tương quan b. Miền thời gian c. Thống kê d. Tần số 10. Tín hiệu nhân quả là tín hiệu: a. khác không khi t<0 b. Bằng không khi t≥0 c. khác không khi t≥0 d. Bằng không khi t<0 11. Tích phân tín hiệu x(t) được tính theo công thức: a.x = x t dt b. x = x t dt 0 0 c. x = x t dt d. x = x t dt 12. Trị trung bình tín hiệu x(t) xác định trong khoảng thời gian t12 ,t có giá trị: 84 1 1 t2 a. x = x t dt b. x = x t dt t -t t -t 21t1 21t1 1 t2 1 c. x = x t dt d. x = x t dt t21 -t t21 -t 13. Năng lượng tín hiệu x(t) được tính theo công thức: a. E = x2 t dt b. E = x2 t dt x x 0 0 c. E = x2 t dt d. E = x2 t dt x x 14. Công suất trung bình tín hiệu x(t) xác định trong khoảng thời gian t12 ,t có giá trị: 1 1 t2 a. x = x2 t dt b. x = x2 t dt t -t t -t 21t1 21t1 1 t2 1 c. x = x2 t dt d. x = x2 t dt t21 -t t21 -t t-c 15. Cho tín hiệu x t = a.Π , ta có: b 2 2 a.x = a.b; Ex = a.b b. x = a.b; Ex = a .b 2 22 c. x = 2ab; Ex = a b d. x = ab; Ex = a b 1 16. Cho tín hiệu x t = Λt , ta có: 2 1 2 a.x = 1; E = b. x = 1; E = x 3 x 3 11 12 c. x = ; E = d. x = ; E = 23x 23x 17. Tín hiệu Sa2 x , ta có: Sin2 x Sin2 x 2 , x 0 , x 0 a.Sa x = x2 b. Sa x = x 0 , x = 0 , x = 0 85 Sin x Sin2 x , x 0 , x 0 c. Sa x = x2 d. Sa x = x2 , x = 0 , x = 0 18. Cho tín hiệu x t = 1 t , ta có: 1 a. x = 1; P = b. x = 1; P = 1 x 2 x 11 1 c. x = ; P = d. x = ; P = 1 22x 2 x 19. Tín hiệu phân bố dirac δt được định nghĩa : 0 , voi t 0 a. δ t = va δ t dt 0 , voi t 0 0 , voi t 0 b. δ t = va δ t dt 1 , voi t 0 0 , voi t 0 c. δ t = va δ t dt 0 , voi t 0 0 , voi t 0 d. δ t = va δ t dt 1 , voi t 0 20. Chọn câu trả lời đúng : t t a. δ = aδ t b. δ = -aδ t a a t t c. δ = a δ t d. δ = aδ t a a 21. Chọn câu trả lời đúng : a. x t *δ t-a = x a b. x t *δ t-a = x t c. x t *δ t-a = x 0 d. x t *δ t-a = x t-a 22. Cho tín hiệu phức x t = e j2t có chu kỳ T, ta có: a. x t = cos 2t + sin 2t b. x t = cos 2t + jsin 2t c. x t = cos 2t - jsin 2t d. x t = jcos 2t + sin 2t 23. Cho tín hiệu có chu kỳ T, ta có công suất trung bình tín hiệu: 1 a. P = 1 b. P = x x 2 c. Px = 2 d. Px = 4 86 24. Tích chập trong miền thời gian sẽ là: a. Phép chập trong miền tần số b. Phép nhân trong miền tần số c. Phép cộng tuyến tính trong miền tần số d. Phép chia trong miền tần số 25. Tích chập trong miền tần số sẽ là: a. Phép chập trong miền thời gian b. Phép nhân trong miền thời gian c. Phép cộng tuyến tính trong miền thời gian d. Phép chia trong miền thời gian t 26. Cho tín hiệu x(t) = 4Π , ta có: 2 a. x = 2 b. x = 4 c. x = 8 d. x = 16 t 27. Cho tín hiệu x(t) = 4 , ta có: 2 a. x = 2 b. x = 4 c. x = 8 d. x = 16 t 28. Cho tín hiệu x(t) = 4Π , ta có năng lượng của x(t) là: 2 a. Ex = 8 b. Ex = 16 c.E x = 32 d.E x = 64 t 29. Cho tín hiệu x(t) = 4 , ta có năng lượng của x(t) là: 2 8 16 a. E = b. E = x 3 x 3 32 64 c. E = d. E = x 3 x 3 1 30. Cho tín hiệu x(t) = .1 t , ta có: 2 1 a. x = 1 b. x = 8 1 1 c. x = d. x = 4 2 1 31. Cho tín hiệu x(t) = .1 t , ta có: 2 1 1 a. P = b. P = x 2 x 16 1 1 c. P = d. P = x 4 x 8 87 t 32. Cho biết x(t) = Π và y(t) = δ(2t) , ta có: 2 1 1 a. x(t).y(t) = δt b. x(t).y(t) = t 2 2 t c. x(t).y(t) = δ d. x(t).y(t) = Π 2t 2 33. Cho biết và y(t) = δ(t) , ta có: 34. Cho tín hiệu x(t) = Π 2t thì phổ X ω bằng a. X ω = 2Sa b. X ω = 2Sa 2 1 1 c. X ω = Sa d. X ω = Sa 22 24 35. Cho tín hiệu x(t) = 4t thì phổ bằng 1 2 1 2 a. X ω = Sa b. X ω = Sa 22 24 1 2 1 2 c. X ω = Sa d. X ω = Sa 28 48 36. Cho tín hiệu x t = 2Sa 2t thì phổ bằng ω a. X ω = . b. X ω = π.Π 24 2 ω c. X ω = π.Π d. X ω = . 4 22 37. Cho tín hiệu x t = 2Sa2 2t thì phổ bằng: ω a. X ω = . b. X ω = π. 24 2 ω c. X ω = π. d. X ω = . 4 22 38. Nếu tín hiệu xt có phổ X ω thì: 1 1 a. x t .cos(2t) X ω+2 -X ω-2 b. x t .cos(2t) X ω+2 +X ω-2 2 2 1 1 c. x t .cos(2t) X ω+2 +X ω-2 d. x t .cos(2t) X ω+2 -X ω-2 2j 2j 88 39. Nếu tín hiệu xt có phổ X ω thì: 1 1 a. x t .sin(2t) X ω+2 -X ω-2 b. x t .sin(2t) X ω+2 +X ω-2 2 2 1 1 c. x t .sin(2t) X ω+2 +X ω-2 d. x t .sin(2t) X ω+2 -X ω-2 2j 2j 40. Nếu tín hiệu xt thì phổ X ω bằng: a. X ω = π.δ ω b. X ω = 2π.δ 2ω ω ω c. X ω = π.δ d. X ω = 2π.δ 2 2 41. Nếu tín hiệu xt thì mật độ phổ x ω bằng: a. ψX ω = 2π.δ ω b. ψX ω = 4π.δ 2ω ω ω c. ψX ω = π.δ d. ψX ω = 4π.δ 2 2 42. Nếu tín hiệu thì hàm tự tương quan ψτx bằng: a. ψX = 2 b. ψX = 4 c. ψX = 8 d. ψX = 16 43. Nếu tín hiệu x t = 2δt thì phổ bằng: a. X ω = 1 b. X ω = 2 c. X ω = 4 d. X ω = 8 44. Nếu tín hiệu x t = 2δt thì mật độ phổ bằng: a. ψX ω = 2 b. ψX ω = 4 c. ψX ω = 8 d. ψX ω = 16 45. Nếu tín hiệu x t = 2δt thì hàm tự tương quan bằng: a. ψX τ = 2δ τ b. ψX τ = 4δ τ c. ψX τ = 8δ τ d. ψX τ = 16δ τ Cho tín hiệu tin tức x(t) = 2.cos(100πt) và tín hiệu sóng mang y(t) = cos(2.106πt) , 1 biết độ sâu điều chế m = , trả lời các câu 46, 47, 48, 49, 50: 2 46. Tín hiệu điều chế AM là: 6 a. yAM t = 2cos 100πt +4 cos(2.10 πt) 6 b. yAM t = 4cos 100πt +2 cos(2.10 πt) 6 c. yAM t = 2cos 100πt +1 cos(2.10 πt) 6 d. yAM t = 1cos 100πt + 2 cos(2.10 πt) 89 47. Phổ của tín hiệu điều chế AM là: 666 a. YAM ω = πδ ω+100π+2.10 π + πδ ω+100π-2.10 π + πδ ω -100π+2.10 π + πδ ω -100π+2.106 π + 4πδ ω - 2.10 6 π + 4πδ ω 2.10 6 π 666 b. YAM ω = 2πδ ω+100π+2.10 π + 2πδ ω+100π-2.10 π + 2πδ ω -100π+2.10 π + 2πδ ω -100π+2.106 π + 4πδ ω - 2.10 6 π + 4πδ ω 2.10 6π 666 c. YAM ω = 4πδ ω+100π+2.10 π + 4πδ ω+100π-2.10 π + 4πδ ω -100π+2.10 π + 4πδ ω -100π+2.106 π + 2πδ ω - 2.10 6 π + 2πδ ω 2.10 6π 666 d. YAM ω = 2πδ ω+100π+2.10 π + 2πδ ω+100π-2.10 π + 2πδ ω -100π+2.10 π + 2πδ ω -100π+2.106 π + πδ ω - 2.10 6 π + πδ ω 2.10 6 π 48. Mật độ phổ của tín hiệu điều chế AM là: 1666 1 1 a. ψAM ω = πδ ω+100π+2.10 π + πδ ω+100π-2.10 π + πδ ω -100π+2.10 π 2 2 2 1 + πδ ω -100π+2.106 π + 8πδ ω - 2.10 6 π + 8πδ ω 2.10 6 π 2 1666 1 1 b. YAM ω = πδ ω+100π+2.10 π + πδ ω+100π-2.10 π + πδ ω -100π+2.10 π 4 4 4 1 + πδ ω -100π+2.106 π + 8πδ ω - 2.10 6 π + 8πδ ω 2.10 6 π 4 666 c. YAM ω = 4πδ ω+100π+2.10 π + 4πδ ω+100π-2.10 π + 4πδ ω -100π+2.10 π + 4πδ ω -100π+2.106 π + 2πδ ω - 2.10 6 π + 2πδ ω 2.10 6π 666 d. YAM ω = 2πδ ω+100π+2.10 π + 2πδ ω+100π-2.10 π + 2πδ ω -100π+2.10 π 11 + 2πδ ω -100π+2.106 π + πδ ω - 2.10 6 π + πδ ω 2.10 6 π 22 49. Công suất của tín hiệu điều chế AM là: a. Px = 6 b. Px = 8 c. Px = 7 d. Px = 9 50. Hệ số hiệu suất năng lượng của tín hiệu điều chế AM là: 1 1 1 1 a. k = b. k = c. k = d. k = 6 8 7 9 90 1 t-1 Cho tín hiệu x(t) = Sa đưa qua mạch lọc có đáp tuyến tần số như hình sau, biết 22 tín hiệu ra của mạch lọc là y(t) = k(t)*x(t). Trả lời các câu hỏi 51, 52, 53, 54, 55: K ω 2 1 ω -1 1 51. Phổ của tín hiệu x(t) là: a. X ω = π.Π ω .e-jω b. X ω π.Π ω .e jω ω -jω ω jω c. X ω π.Π .e d. X ω π.Π .e 2 2 52. Quá trình thời gian k(t) của K ω là: 1 22 t 2 12 t a. k(t) = Sa t + Sa b. k(t) = Sa t + Sa π π 2 π π 2 1 t 2 2 2 t 1 2 c. k(t) = Sa + Sa t d. k(t) = Sa + Sa t π 2 π π 2 π 53. Phổ của tín hiệu ra y(t) của mạch lọc là: 3ππ a. Y ω = .Π ω .e-jω . 2ω .e -jω 22 π 3π b. Y ω = .Π ω .e-jω . 2ω .e -jω 22 3π-jω π ω -jω c. Y ω = .Π ω .e . .e 2 2 2 3π ω-jω π -jω d. Y ω = .Π .e . .e 2 2 2 54. Tín hiệu ra y(t) của mạch lọc là: 3 t-1 12 t-1 1 t-1 32 t-1 a. y(t) = Sa + Sa b. y(t) = Sa + Sa 4 2 8 4 8 2 4 4 3 t-1 1 2 3 12 t-1 c. y(t) = Sa + Sa t-1 d. y(t) = Sa t-1 + Sa 2 2 4 2 4 2 55. Năng lượng của tín hiệu ra y(t) của mạch lọc là: 37 37 27 27 a. E b. E c. E d. E y 24 y 12 y 24 y 12 91 TÀI LIỆU THAM KHẢO [1]. Lại Nguyễn Duy, Nguyễn Phú Quới, Giáo trình Lý thuyết tín hiệu, Trường Cao đẳng Kỹ thuật Cao Thắng, 2014. [2]. Phạm Thị Cư, Lý thuyết tín hiệu, Nhà xuất bản Đại học Quốc gia TP. Hồ Chí Minh, 2010. [3]. Yuriy Shmaliy, Continuous Time Signal, Springer, 2006. [4]. Bernd Girod, Signals and Systems, John Willey & Sons, 2001. 92
File đính kèm:
 giao_trinh_tin_hieu_va_he_thong_phan_2.pdf
giao_trinh_tin_hieu_va_he_thong_phan_2.pdf

