Giáo trình Tín hiệu và hệ thống (Phần 1)
1.1. TÍN HIỆU
1.1.1. Khái niệm tín hiệu (Signal)
Tín hiệu là biểu diễn vật lý của thông tin mà nó sẽ truyền từ nơi phát (nguồn) đến
nơi nhận (thu).
Các dạng tín hiệu vật lý được quan tâm chủ yếu:
• Dòng điện, điện áp trong các mạch điện- điện tử.
• Sóng điện từ được bức xạ trong các hệ thống thông tin vô tuyến.
• Nhiễu trong các hệ thống điện tử thông tin.
Ví dụ: Tín hiệu âm thanh (voice), hình ảnh (video), tín hiệu vệ tinh, di động.
1.1.2. Khái niệm nhiễu (Noise)
Nhiễu là tín hiệu không mong muốn, tác động đến hệ thống tín hiệu mà chúng ta
đang quan tâm.
Lưu ý: Bản thân nhiễu cũng là một tín hiệu - tín hiệu nhiễu.
Ví dụ: Nhiễu nền, nhiễu xuyên kênh,
1.2. PHÂN LOẠI TÍN HIỆU
1.2.1. Tín hiệu vật lý và tín hiệu mô hình toán học
Tín hiệu vật lý: biểu diễn của một quá trình vật lý (thực hiện được).
Yêu cầu:
• Năng lượng hữu hạn
• Biên độ hữu hạn và liên tục
• Phổ hữu hạn
Tín hiệu mô hình: là các hàm (thực, phức, dùng để đơn giản hơn cho quá trình
biểu diễn, phân tích và xử lý tín hiệu.
Chất lượng của mô hình phụ thuộc vào chất lượng của việc xấp xỉ gần đúng được
ứng dụng đang khảo sát và tính thuận tiện khi áp dụng.
Lưu ý: Tín hiệu mô hình không bị ràng buộc bởi các yêu cầu như trên.
Ví dụ: Tín hiệu vật lý như âm thanh (voice), hình ảnh (video); tín hiệu mô hình
như tín hiệu xung vuông, mũ, sin,
1.2.2. Tín hiệu xác định và tín hiệu ngẫu nhiên
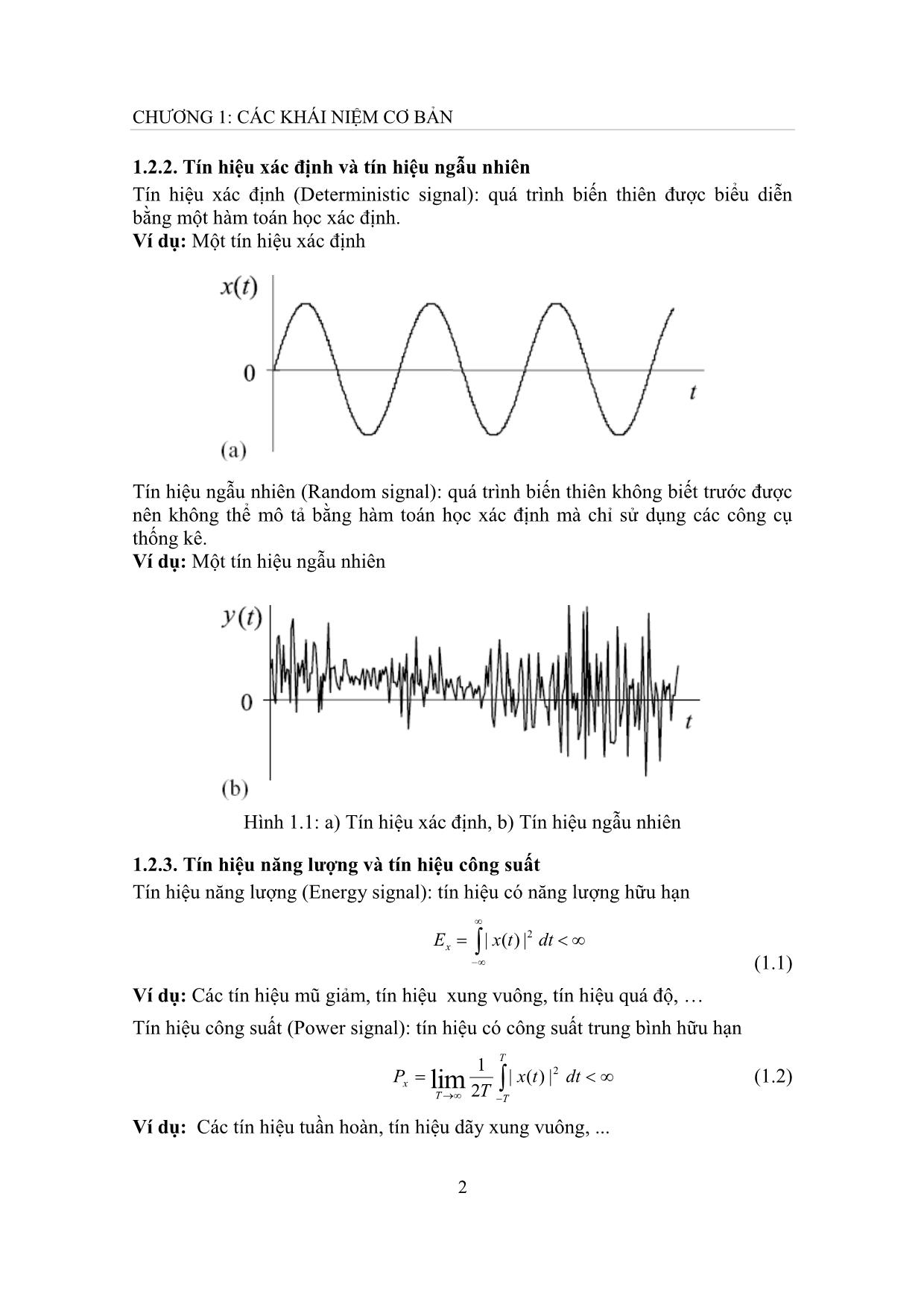
Tín hiệu xác định (Deterministic signal): quá trình biến thiên được biểu diễn
bằng một hàm toán học xác định.
Ví dụ: Một tín hiệu xác định
Tín hiệu ngẫu nhiên (Random signal): quá trình biến thiên không biết trước được
nên không thể mô tả bằng hàm toán học xác định mà chỉ sử dụng các công cụ
thống kê.
Ví dụ: Một tín hiệu ngẫu nhiên

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
Trang 7
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Giáo trình Tín hiệu và hệ thống (Phần 1)

: X()() x t e jt dt (3.1) X() được gọi là phổ của tín hiệu x(t). Biến đổi Fourier ngược: 1 x()() t X ejt d 2 (3.2) Ký hiệu cặp biến đổi Fourier: F x()() t X (3.3) Tổng quát, phổ X() là một hàm phức Phân tích thành các phổ thành phần X ()() X e j () X()()() P jQ (3.4) Ví dụ: Hãy xác định và vẽ phổ của tín hiệu x(t) Áp dụng công thức biến đổi Fourier: 30 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ X()() x t e jt dt T T /2 e jt A.. e jt dt A 2 T /2 j T 2 sinT AT. 2 T 2 T ATSa 2 T |X ( ) | AT Sa 2 Vẽ biên độ phổ và pha: 3.1.2 Tính chất Tính chất chẵn lẻ: Nếu x(t) là hàm thực: Phổ biên độ |X()|: hàm chẵn Phổ pha (): hàm lẻ Phổ thực Q(): hàm chẵn Phổ ảo P(): hàm lẻ Quan hệ: 31 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ x( t ) F X ( ); FF x()()()() t X x t X x ()() t F X Ví dụ: Các cặp biến đổi Fourier 1 x( t ) e t 1( t ) X ( ) j 1 x( t ) e t 1( t ) X ( ) j Tính chất tuyến tính: x( t ) FF X ( ); x ( t ) X ( ) Nếu 1 1 2 2 axtaxt( ) ( ) F aX ( ) aX ( ), aa , Thì: 1 1 2 2 1 2 2 1 2 (3.4) Ví dụ: Xác định phổ của tính hiệu sau: tt3 x( t ) 3 e 2 e aa12 3& 2 t F 2 6 12 x11()()() t e X 2 X 2 2 1 1 9 6 x()() t e t F X 222 9 Tính chất đối ngẫu: x( t ) X ( ) X ( t ) 2 x ( ) (3.5) Tính chất thay đổi thang đo: t x() t X () x () a X (); a a 0; a (3.6) 32 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Ví dụ: tT TSa() T 2 3t T T Sa( ); a 1/ 3 T 36 tT3 3TSa ( ); a 3. 32T Tính chất dịch chuyển trong miền thời gian: x()()()() t X x t t X e jt 0 0 (3.7) Tính chất dịch chuyển trong miền tần số: jt0 x()() t e X 0 x()() t X (3.8) jt0 x()() t e X 0 Tính chất điều chế: 1 x( t )cos(o t ) X ( o ) X ( o ) 2 1 x( t )sin(o t ) X ( o ) X ( o ) 2 j (3.9) Ví dụ: Cho x(t) có phổ như hình vẽ. Vẽ phổ của tín hiệu y(t)=x(t).cos0t. Tính chất tính chập: x()()()() t y t X Y 1 x( t ) y ( t ) [ X ( ) Y ( )] 2 (3.10) 33 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Định nghĩa tính chập: xt()()()() yt xtyttdt''' (3.11) 3.2 PHỔ CỦA MỘT SỐ TÍN HIỆU THÔNG DỤNG 3.2.1 Phổ của tín hiệu năng lượng Xung vuông: tT TSa() T 2 (3.12) Hình 3.1: Phổ tín hiệu xung vuông Xung tam giác: tT2 TSa () T 2 (3.13) 34 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Hình 3.2: Phổ tín hiệu xung tam giác Hàm Sa: Sa()0 t 2 00 (3.14) Hình 3.3: Phổ hàm Sa Hàm Sa2: 2 Sa()0 t 2 00 (3.15) Hình 3.4: Phổ hàm Sa2 Hàm e- |t|: t 2 e 22 (3.16) 35 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Hình 3.5: Phổ hàm e- |t| Hàm (t): (t ) 1 (3.17) Hình 3.6: Phổ hàm (t) 3.2.2 Phổ của tín hiệu công suất trung bình hữu hạn Hàm x(t)=1: 1 2 ( ) (3.18) Hình 3.7: Phổ hàm x(t) = 1 36 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Hàm u(t): 1 ut()() j (3.19) Hình 3.8: Phổ hàm u(t) Hàm ej0t: e jt0 2 ( ) 0 (3.20) Chứng minh: Hình 3.9: Phổ hàm ej0t 3.2.3 Phổ của tín hiệu tuần hoàn Phổ của tín hiệu cos tuần hoàn với chu kỳ T là: (3.21) Cos()()()0 t 0 0 Hình 3.10: Phổ hàm cos 37 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Phổ của tín hiệu sin tuần hoàn với chu kỳ T là: (3.22) Sin()()()0 t j 0 0 Hình 3.11: Phổ hàm sin Dùng khai triển Fourier dạng phức: jn0 t 2 x(); t Xn e 0 n T Trong đó: 1 tT0 X x( t ) e jn0 t dt ; n 0, 1, 2, 3,... n T t 0 Phổ của tín hiệu tuần hoàn có dạng: (3.23) X( ) 2 Xn ( n 0 ) n Chứng minh: Áp dụng công thức sau cho biểu thức (*) ở trên. (3.24) e jt0 2 ( ) 0 Cách xác định hệ số Xn: Cách 1: Sử dụng công thức (**) Cách 2: i. Xét tín hiệu XT(t) trong một chu kỳ T, t€[t0,t0+T]. ii. Xác định XT() dùng biến đổi Fourier cho XT(t). iii. Xn = XT(n0)/T. 38 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Phổ của dãy xung vuông đơn cực: Vì x(t) là tín hiệu tuần hoàn, nên phổ có dạng: X( ) 2 Xn ( n 0 ) n Xác định hệ số phổ Xn: Cách 1: sử dụng công thức (**)\ T /2 /2 11 jn t jn t X x() t e00 dt Ae dt n TT T /2 /2 A San A San TTT0 2 Cách 2: t Ta có : xTT ( t ) A X ( ) A Sa ( ) 2 n0 Xn() A Sa() T 0 2 X n TT A n2 n Sa()() A Sa TTTT2 Suy ra, biểu thức phổ: (3.25) X( ) 2 A Sa ( n ) ( n 0 ) n TT 39 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Hình 3.12: Phổ dãy xung vuông đơn cực Phổ của phân bố lược: 1 t xt( ) ||| TT Vì x(t) là tín hiệu tuần hoàn, nên phổ có dạng: X( ) 2 Xn ( n 0 ) n Xác định hệ số phổ Xn: Cách 1: sử dụng công thức (**) TT/2 /2 1 jn00 t 1 1 t jn t Xn x( t ) e dt ||| e dt TTTT TT/2 /2 11T /2 ()t e jn0 t dt TT T /2 40 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Cách 2: Suy ra, biểu thức phổ: 2 X( ) 2 X ( n ) ( n ) n 00 nn T Như vậy: 1 t (3.26) ||| ||| TT 0 Hình 3.12: Phổ phân bố lược Ví dụ: Xác định phổ của tín hiệu tuần hoàn sau: Hướng dẫn: 41 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ 3.3 MẬT ĐỘ PHỔ 3.3.1 Mật độ phổ năng lượng ESD (Energy Spectrum Density) Đặc trưng cho phân bố năng lượng tín hiệu trong miền tần số : ()()X 2 (3.27) Quan hệ giữa ESD và hàm tự tương quan: ()() ed j F ()() , nghĩa là: 1 ()() edj 2 Định lý Parseval về năng lượng: 2 1 x()() t dt d (3.28) 2 Các cách tính năng lượng của một tín hiệu: Từ định nghĩa: (3.29) E x() t2 dt x Từ hàm tự tương quan: E (0) (3.30) x Từ định lý Parseval : 1 Ed () x (3.31) 2 Ví dụ: Cho tín hiệu sau. Hãy xác định () và Ex. 1 x()()() t e t u t X j 42 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Tính năng lượng: 2 2 11 ()() X j 22 1 Ed () x 2 1 1 1 d 22 22 3.3.2 Mật độ phổ công suất PSD (Power Spectrum Density) Đặc trưng cho phân bố công suất tín hiệu trong miền tần số » T () , trong đó: ( ) lim T T Quan hệ giữa PSD và hàm tự tương quan: F ()() Định lý Parseval về công suất : T /2 112 (3.32) PxT lim x ( t ) dt ( ) d T T T /2 2 Các cách tính công suất của một tín hiệu: Từ định nghĩa: T /2 (3.33) 1 2 PxT lim x ( t ) dt T T T /2 Từ hàm tự tương quan: (3.34) Px (0) Từ định lý Parseval : 1 Pd () (3.35) x 2 43 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Ví dụ: Cho tín hiệu sau. Hãy xác định PSD và Px. t t T /4 xT ()() t u t TT /2 TT jT /4 XT () Sa e 24 2 2 TT2 ()() X Sa T 44 2 T () TT2 ( ) lim limSa ( ) TT T 44 Tính công suất: 1 1 1 P ()() d d x 2 2 2 3.3.3 Mật độ phổ công suất của tín hiệu tuần hoàn Phổ của tín hiệu tuần hoàn: X( ) 2 Xn ( n 0 ) n PSD của nó có dạng: 2 (3.36) ( ) 2 Xnn ( n 00 ) 2 ( n ) nn Định lý Parseval đối với tín hiệu tuần hoàn: 1 P ( ) d | X |2 (3.37) xn 2 n Cách tính công suất Px: (tương tự phần 3.3.2) Ví dụ: Cho tín hiệu sau x(t)=cos0t. Hãy xác định PSD và Px. XA() 00 AA 2 00 22 AA22 ( ) 2 00 4444 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ Tính công suất: AAA2 2 2 P xn n 4 4 2 Hoặc: 1 T A2 P A22cos tdt x 0 T 0 2 BÀI TẬP CHƯƠNG 3 Câu 1: Xác định phổ và tính năng lượng các tín hiệu sau: a) x(t) 1 -6 -2 0 2 6 8 10 t b) x(t) 1 t -T -T/4 0 T/4 T Câu 2: Xác định phổ và tính năng lượng các tín hiệu sau: xt xt 2 2 t t 1 1 1 1 a) 2 2 b) 2 2 45 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ xt 1 t 3 2 1 0 1 2 3 c) xt 1 t 3 2 1 0 1 2 3 d) xt 2 t 2 0 2 e) xt 6 2 t 2 0 2 f) Câu 3: Xác định phổ và tính năng lượng các tín hiệu sau: t 10 t 10 a) x t 10. 10. 10 10 t 10 t 10 b) x t 10. 10. 10 10 46 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ tt c) x t 10. 10 10 5 d) x t 2.u t 2 e) x t 2.u t 2 f.) x t 2.u t 2 2.u t 2 Câu 4: Xác định phổ và tính năng lượng các tín hiệu sau: t 10 a) x t 5 4 t6 b) x t 3 3 t 10 c) x t 5 4 t6 d) x t 3 3 e) x t 2.e t .u t 2 f) x t 2.e t .u t 2 Câu 5: Tính công suất tín hiệu x(t)=10cos 10t +20cos 20t theo 2 cách:. a) Tính trực tiếp trong miền thời gian b) Tính dựa trên hàm mật độ phổ tín hiệu Câu 6: Cho tín hiệu x(t) có phổ cho trên hình sau: a) Xác định quá trình thời gian x(t). b) Tính năng lượng tín hiệu x(t). 47 CHƯƠNG 3: PHÂN TÍCH TÍN HIỆU MIỀN TẦN SỐ X X 6 2 2 2 0 2 2 0 2 a) b) Câu 7: Cho x(t) cos 2t 3sin 3t 4cos5t . Xác định: a) Phổ của tín hiệu x(t). b) Hàm mật độ phổ và công suất tín hiệu x(t). t Câu 8: Cho x(t) t T a) Xác định phổ tín hiệu X(w). b) Xác định năng lượng tín hiệu trong miền thời gian c) Xác định năng lượng tín hiệu trong miền tần số Câu 9: Cho các tín hiệu x(t) = Sa2t và y(t) = Sa4t a) Xác định và vẽ phổ của x(t), y(t). b) Xác định mật độ phổ của x(t), y(t). c) Tính Ex, Ey. Câu 10: Tìm quá trình thời gian x(t) của tín hiệu có phổ cho sau: X() K() 2 4π 2π 1 -1 1 -10 -8 -6 0 6 8 10 48 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ CHƯƠNG 4 TRUYỀN TÍN HIỆU QUA MẠCH TUYẾN TÍNH 4.1 TÍCH CHẬP (CONTINUOUS TIME CONVOLUTION) 4.1.1 Định nghĩa Tích chập giữa hai tín hiệu x(t) và y(t), ký hiệu: x(t)*y(t), được xác định như sau: x(t) * y(t) x( )y(t )d (4.1) (*) Xét hai tín hiệu x(t) và h(t), tích chập y(t)=x(t)*h(t) được xác định theo (4.1). 4.1.2 Các tính chất Tính chất giao hoán: x(t)* y(t) y(t)* x(t) Tính chất kết hợp: x(t)*[y(t)* z(t)] [x(t)* y(t)]* z(t) Tính chất phân phối: 49 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ x(t)*[y(t) z(t)] x(t)* y(t) x(t)* z(t) Nhân với hằng số: a[x(t)* y(t)] [ax(t)]* y(t) x(t)*[ay(t)] Liên hệ với hàm tương quan: ( ) x(t)y* (t )dt x( )* y* ( ) xy 4.2 HỆ THỐNG TUYẾN TÍNH BẤT BIẾN LTI (LINEAR TIME INVARIANT SYSTEM) 4.2.1. Định nghĩa LTI là hệ thống thỏa mãn đồng thời tính chất tuyến tính và bất biến. Tính chất tuyến tính: Tính chất bất biến: 4.2.2 Đáp ứng xung và đáp ứng tần số Đáp ứng xung (Impulse response): Đáp ứng xung là tín hiệu ngõ ra của hệ thống khi tín hiệu ngõ vào là xung (t). Đáp ứng xung h(t) đặc trưng cho hệ thống trong miền thời gian. 50 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ Hình 4.1: Hệ thống tuyến tính bất biến Đáp ứng tần số (Frequency response): đặc trưng cho hệ thống trong miền tần số. Biến đổi Fourier của đáp ứng xung, nghĩa là: F h()() t H H()() h t e jt dt (4.2) Chú ý: 4.3 QUAN HỆ GIỮA CÁC ĐẶC TRƯNG TÍN HIỆU 4.3.1 Ý nghĩa của tích chập Phép tính tích chập giúp xác định tác động của hệ thống lên tín hiệu ngõ vào. Nghĩa là, nó giúp xác định tín hiệu ngõ ra của hệ thống LTI khi biết tín hiệu ngõ vào và đáp ứng xung của hệ thống. 4.3.2 Biểu thức quan hệ Hình 4.2: Quan hệ hàm truyền Trong miền thời gian: 51 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ y()()() t h t x t (4.3) Nghĩa là: y()()()()() t x h t d h x t d (4.4) Trong miền tần số: YHX()()() (4.5) Nghĩa là: YHX()().() YHX()()() Hàm tự tương quan: ()()()() hh * yy xx Mật độ phổ: ()().() H 2 yx (Tín hiệu năng lượng) ()()() H 2 yx (Tín hiệu công suất) H( n )2 ; n 0, 1, 2,... yn0 xn (Tín hiệu tuần hoàn) 4.3.3 Một số ví dụ Ví dụ 1: Xác định y(t) và Ey. 2 x( t ) Sa (2 t ) H () 4 52 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ Lời giải: Xác định phổ của tín hiệu ngõ vào: 2 x( t ) Sa (2 t ) X ( ) 24 Xác định phổ tín hiệu ngõ ra: YXH()()() 2 4 4 1 1 1 1 2 2 4 2 2 2 2 4 4 2 Tín hiệu ngõ ra: 11 y( t ) S a2 t Sa2 t 24 Năng lượng tín hiệu ngõ ra: 1 12 1 7 E | Y ( ) |22 d | 1| d y 2 4 4 24 0 Ví dụ 2: Cho tín hiệu x(t) qua hệ thống có đáp ứng như hình vẽ. 2 x( t ) 2cos t 4cos t .cos2 t 53 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ a. Xác định phổ X(). b. Xác định phổ Y(). c. Tính công suất Py. Lời giải: a. Phổ tín hiệu ngõ vào: x( t ) 1 cos 2 t 2cos t 2cos3 t 1 2cost cos 2 t 2cos3 t X ()2 ()2[ ( 1) ( 1)][ ( 2) ( 2)] 2[ ( 3) ( 3)] 2( 3) ( 2)2( 1)2() 2( 1) ( 2)2( 3) b. Phổ tín hiệu ngõ ra: j Y() X ()()[2 H ( 3) ( 2)2 ( 1)] e 2 j 2 [2 ( 1) ( 2) 2 ( 3)]e . 54 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ c. Công suất tín hiệu ngõ ra: Xác định mật độ phổ công suất: 11j Ye()2[( 3) ( 2) ( 1)] 2 22 11 j 2 [ ( 3) ( 2) ( 1)]e 2 22 11 ()2[( 3) ( 2) ( 1)] y 44 11 2 [ ( 3) ( 2) ( 1)] 44 Công suất: 1 1 1 1 Py yn 1 1 3 n 4 4 4 4 BÀI TẬP CHƯƠNG 4 Câu 1: Cho tín hiệu x(t) 2e 3t1(t) đi qua hệ thống có đáp ứng xung k(t) Sa4t . 55 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ a) Xác định phổ X (w) của tín hiệu ngõ ra x(t) . b) Xác định phổ Y(w) của tín hiệu ngõ ra y(t) . c) Xác định mật độ phổ năng lượng của x(t) và y(t). Câu 2: Cho tín hiệu x t 2Sa 2t được đưa qua mạch lọc có đặc tuyến tần số K như hình vẽ sau: K 3 3 0 3 a) Xác định phổ X( ) của tín hiệu ngõ ra . b) Xác định phổ Y( ) của tín hiệu ngõ ra . c) Xác định tín hiệu ngõ ra y(t). d) Tính năng lượng của y(t). Câu 3: Cho tín hiệu x t 2Sa2 2t được đưa qua mạch lọc có đặc tuyến tần số như hình vẽ sau: K 2 2 0 2 a) Xác định phổ của tín hiệu ngõ ra . b) Xác định phổ của tín hiệu ngõ ra . c) Xác định tín hiệu ngõ ra y(t). d) Tính năng lượng của y(t). 56 CHƯƠNG 5: TÍN HIỆU ĐIỀU CHẾ Câu 4: Cho tín hiệu x t 2Sa2 t được đưa qua mạch lọc có đặc tuyến tần số K như hình vẽ sau: K 1 3 0 3 a) Xác định phổ X( ) của tín hiệu ngõ ra x(t) . b) Xác định phổ Y( ) của tín hiệu ngõ ra y(t) . c) Xác định tín hiệu ngõ ra y(t). d) Tính năng lượng của y(t). Câu 5: Ở đầu vào của mạch lọc, có đặc tuyến tần số K(w) A(w)e j (w) biểu diễn như hình vẽ. Được đưa đến tín hiệu x(t). Hãy xác định và vẽ phổ biên độ, phổ pha của tín hiệu ở đầu ra mạch lọc y(t). Tính Px, Py của tín hiệu x(t), y(t) tương ứng trong các trường hợp sau: A(w) (w) 1 /2 w w 0 -2 0 2 - /2 a) x(t) = 2 b) x(t) = 2.1(t) d) x(t) = 2sin(t) c) x(t) = 2cos(t) e) x(t) = 2cos2t + 4cos(t)cos(2t) 57
File đính kèm:
 giao_trinh_tin_hieu_va_he_thong_phan_1.pdf
giao_trinh_tin_hieu_va_he_thong_phan_1.pdf

