Giáo trình Lý thuyết thông tin
1: Mục tiêu
Sau khi hoàn tất bài học này bạn có thể biết:
- Đối tượng nghiên cứu,
- Mô hình lý thuyết thông tin theo quan điểm Shannon,
- Các khái niệm về Lượng tin biết và lượng tin chưa biết,
- Định lý cơ sở của kỹ thuật truyền tin,
- Khái niệm chung về dung lượng kênh truyền,
- Vấn đề sinh mã và giải mã.
Đối tượng nghiên cứu
Lý thuyết thống kê về thông tin được xây dựng trên hai hướng khác nhau bởi hai nhà toán học
Shannon (1948) và Wiener (1949). Lý thuyết thông tin nghiên cứu quá trình xử lý tín hiệu như
sau:
Đầu vào (input): nhận tín hiệu từ một lĩnh vực cụ thể, tức là tín hiệu xuất hiện theo các ký hiệu
(symbol) từ một tập hợp cho trước và theo phân phối xác suất đã biết.
Tín hiệu được truyền đi trên kênh truyền (channel) và có thể bị nhiễu cũng theo một phân phối
xác suất nào đó. Kênh truyền có thể được hiểu dưới hai nghĩa:
Dưới nghĩa vật lý: kênh truyền là một hệ thống truyền tín hiệu (dây dẫn, mạch, sóng, .) và gây
nhiễu tùy thao chất lượng của hệ thống.
Dưới nghĩa toán học: kênh truyền là các phân phối xác suất xác định trên lớp các tín hiệu đang xét
ở đầu nhận tín hiệu (output).
Ở đầu ra (output): dựng lại tín hiệu chân thật nhất có thể có so với tín hiệu ở đầu vào.
Shannon xây dựng mô hình lý thuyết thông tin trên cơ sở giải quyết bài toán: sinh mã độ dài tối
ưu khi nhận tín hiệu đầu vào. Tín tối ưu được xét trên 3 yếu tố sau:
Phân phối xác suất của sự xuất hiện của các tín hiệu.
Tính duy nhất của mã và cho phép tự điều chỉnh mã sai nếu có với độ chính xác cao nhất. Giải mã
đồng thời tự động điều chỉnh mã hoặc xác định đoạn mã truyền sai.
Trong khí đó, Wiener lại nghiên cứu phương pháp xử lý tín hiệu ở đầu ra: ước lượng tối ưu chuỗi
tín hiệu so với chính nó khi nhận ở đầu vào không qua quá trình sinh mã. Như vậy phương pháp
Wiener được áp dụng trong những trường hợp con người không kiểm soát được quá trình truyền
tín hiệu. Môn “xử lý tín hiệu” đã đề cập đến vấn đề này.
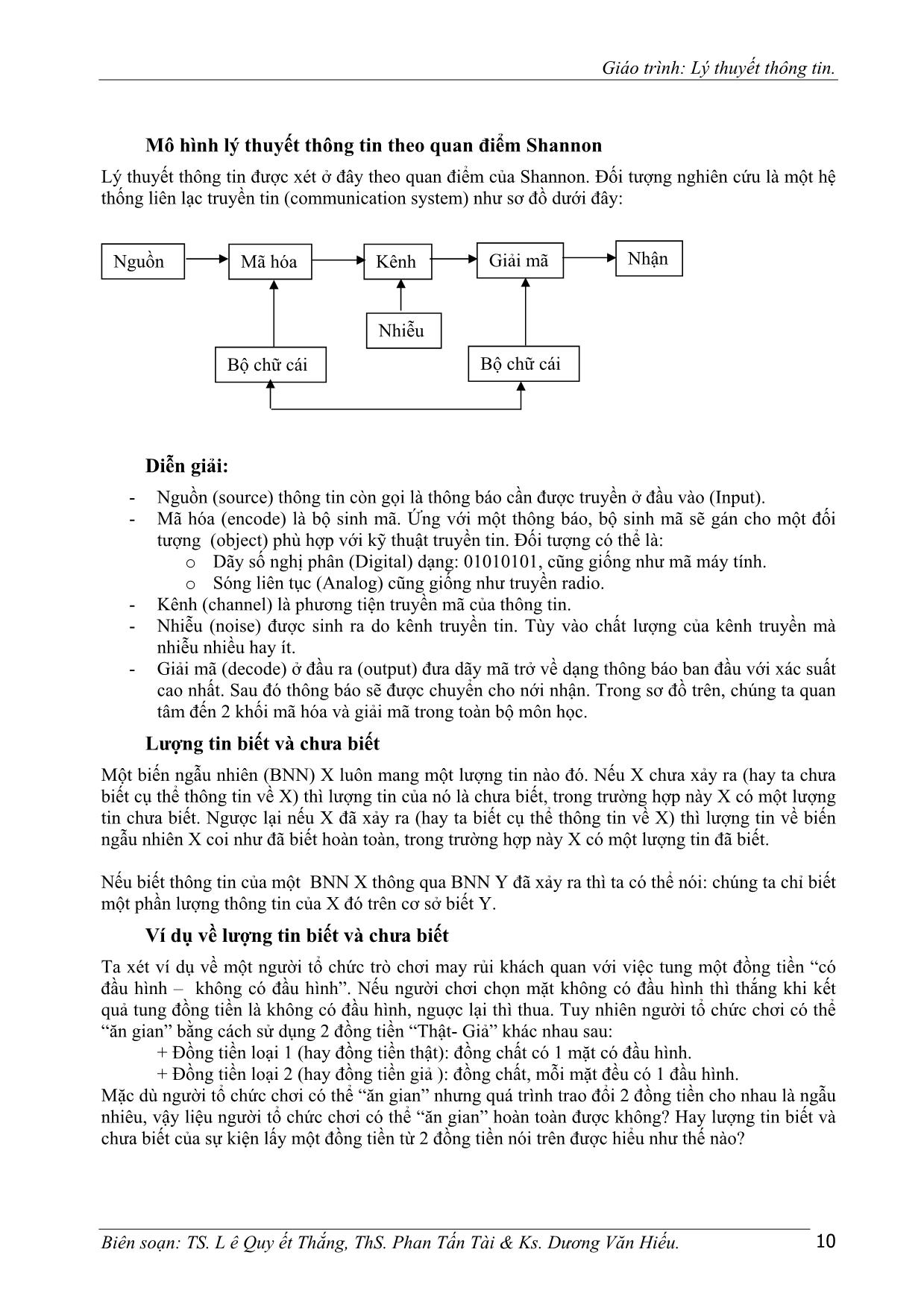
Diễn giải:
- Nguồn (source) thông tin còn gọi là thông báo cần được truyền ở đầu vào (Input).
- Mã hóa (encode) là bộ sinh mã. Ứng với một thông báo, bộ sinh mã sẽ gán cho một đối
tượng (object) phù hợp với kỹ thuật truyền tin. Đối tượng có thể là:
o Dãy số nghị phân (Digital) dạng: 01010101, cũng giống như mã máy tính.
o Sóng liên tục (Analog) cũng giống như truyền radio.
- Kênh (channel) là phương tiện truyền mã của thông tin.
- Nhiễu (noise) được sinh ra do kênh truyền tin. Tùy vào chất lượng của kênh truyền mà
nhiễu nhiều hay ít.
- Giải mã (decode) ở đầu ra (output) đưa dãy mã trở về dạng thông báo ban đầu với xác suất
cao nhất. Sau đó thông báo sẽ được chuyển cho nới nhận. Trong sơ đồ trên, chúng ta quan
tâm đến 2 khối mã hóa và giải mã trong toàn bộ môn học.
Lượng tin biết và chưa biết
Một biến ngẫu nhiên (BNN) X luôn mang một lượng tin nào đó. Nếu X chưa xảy ra (hay ta chưa
biết cụ thể thông tin về X) thì lượng tin của nó là chưa biết, trong trường hợp này X có một lượng
tin chưa biết. Ngược lại nếu X đã xảy ra (hay ta biết cụ thể thông tin về X) thì lượng tin về biến
ngẫu nhiên X coi như đã biết hoàn toàn, trong trường hợp này X có một lượng tin đã biết.
Nếu biết thông tin của một BNN X thông qua BNN Y đã xảy ra thì ta có thể nói: chúng ta chỉ biết
một phần lượng thông tin của X đó trên cơ sở biết Y.
Ví dụ về lượng tin biết và chưa biết
Ta xét ví dụ về một người tổ chức trò chơi may rủi khách quan với việc tung một đồng tiền “có
đầu hình – không có đầu hình”. Nếu người chơi chọn mặt không có đầu hình thì thắng khi kết
quả tung đồng tiền là không có đầu hình, nguợc lại thì thua. Tuy nhiên người tổ chức chơi có thể
“ăn gian” bằng cách sử dụng 2 đồng tiền “Thật- Giả” khác nhau sau:
+ Đồng tiền loại 1 (hay đồng tiền thật): đồng chất có 1 mặt có đầu hình.
+ Đồng tiền loại 2 (hay đồng tiền giả ): đồng chất, mỗi mặt đều có 1 đầu hình.
Mặc dù người tổ chức chơi có thể “ăn gian” nhưng quá trình trao đổi 2 đồng tiền cho nhau là ngẫu
nhiêu, vậy liệu người tổ chức chơi có thể “ăn gian” hoàn toàn được không? Hay lượng tin biết và
chưa biết của sự kiện lấy một đồng tiền từ 2 đồng tiền nói trên được hiểu như thế nào?

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Giáo trình Lý thuyết thông tin

ứng.
- Tìm bộ mã xoay vòng theo phương pháp sinh nhanh bộ mã xoay vòng
2. Cho thanh ghi lùi từng bước sau:
+ F3 F2 F1 F0
- Tìm ma trận kiểm tra chẵn lẻ có số cột n > 4
- Từ kết quả câu a, xác định bộ mã xoay vòng tương ứng.
- Tìm bộ mã xoay vòng theo phương pháp sinh nhanh bộ mã xoay vòng.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 85
Giáo trình: Lý thuyết thông tin.
BÀI 5.9: ĐA THỨC ĐẶC TRƯNG CỦA THANH GHI
Mục tiêu
Sau khi hoàn tất bài học này bạn có thể:
- Hiểu định nghĩa đa thức đặc trưng của thanh ghi,
- Hiểu Quan hệ giữa chu kỳ n, đa thức đặc trưng và đa thức (xn + 1),
- Vận dụng sinh thanh ghi lùi từng bước,
- Làm cơ sở để vận dụng sinh bộ mã vòng.
Định nghĩa đa thức đặc trưng của thanh ghi
Định nghĩa: đa thức đặc trưng của thanh ghi có ma trận đặc trưng là T là đa thức có dạng
2 m-1 m
gm(x)=a0 + a1x+ a2 x + +am-1x + x .
với a0, a1, a2,, am-1 là các công tắc của thanh ghi và m là số bit của thanh ghi
Ví dụ: xét lại thanh ghi như hình sau:
+ F3 F2 F1 F0
a0 = 1, a1= 0, a2 = 1, a3 = 0
2 4
Đa thức đặc trưng của thanh ghi có dạng: gm(x)=1 + x + x .
Quan hệ giữa chu kỳ n, đa thức đăc trưng và đa thức (xn + 1)
2 m-1 m n
Đa thức đặc trưng của thanh ghi gm(x)=a0 + a1x+ a2 x + +am-1x + x luôn chia hết đa thức (x
+ 1).
Ví dụ: xét lại thanh ghi lui từng bước như hình sau:
F F F F
+ 3 2 1 0
Từ thanh ghi ta có thể xác định các kết quả sau:
- a0 = 1, a1= 0, a2 = 1, a3 = 0
2 4
- Đa thức đặc trưng của thanh ghi có dạng: g4(x)=1 + x + x .
- Thanh ghi này có chu kỳ n = 6.
Thực hiện phép chia đa thức (x6 + 1) : (1 + x2 + x4) = (x2 + 1) ⇒ chia hết.
Ghi chú: phép toán trên đa thức nhị phân vẫn là phép toán Modulo 2.
Ví dụ: xét lại thanh ghi lui từng bước như hình sau:
F F F F
+ 3 2 1 0
a0 = 1, a1= 0, a2 = 1, a3 = 0
2 4
đa thức đặc trưng của thanh ghi có dạng: g4(x)=1 + x + x .
thanh ghi này có chu kỳ n = 6 và (x6 + 1) : 1 + x2 + x4 = x2 + 1.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 86
Giáo trình: Lý thuyết thông tin.
Thủ tục sinh thanh ghi lùi từng bước
Để sinh thanh ghi lùi từng bước với số bit là m và có chu kỳ n, ta có thể thực hiện theo các bước
sau:
Bước 1: xác định đa thức đặc trưng của thanh ghi
2 m-1 m
- Tìm 2 đa thức gm(x)=a0 + a1x+ a2 x + +am-1x + x
2 k-1 k n
và hk(x)=h0 + h1x+ h2x + +hk-1x + x sao cho (x + 1) = gm(x)* hk(x).
n
- Nếu ∃ (x + 1) = gm(x)* hk(x) thì ta chọn gm(x) làm đa thức đặc trưng cho thanh ghi (vì
số bit kiểm tra của bộ mã là m) và thực hiện bước 2.
- Ngược lại: không tồn tại thanh ghi theo yêu cầu.
Bước 2: vẽ thanh ghi
2 m-1 m
Từ gm(x)=a0 + a1x+ a2 x + +am-1x + x ⇒ a0, a1, a2,, am-1 ⇒ thanh ghi có dạng:
+ Fm-1 Fm-2 F1 F0
a
m-1 am-2 a1 a0
Ví dụ minh họa
Thiết kế thanh ghi có m=3 bit và chu kỳ n=7, ta thực hiện theo 2 bước sau:
Bước 1: Xác định đa thức đặc trưng của thanh ghi
Ta có (x7 + 1) : (1 + x2 + x3) = (1 + x2 + x3 + x4)
2 3
Do m=3 nên chọn g3(x) = (1 + x + x ) làm đa thức đặc trưng của thanh ghi.
Bước 2: Vẽ thanh ghi
2 3
Từ g3(x) = (1 + x + x ) ta có, a0=1, a1=0, a2=1
+ F2 F1 F0
Bài tập
1. Trong các thanh ghi sau đây, thanh ghi nào sinh ra bộ mã vòng có độ dài n=15 bit?
(R1): + F3 F2 F1 F0
(R2): + F3 F2 F1 F0
(R3): + F3 F2 F1 F0
2. Nêu các bước cần thiết để thiết kế bộ mã xoay vòng độ dài 15 bit với số bit kiểm tra là 4.
Vẽ sơ đồ thanh ghi dạng tổng quát.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 87
Giáo trình: Lý thuyết thông tin.
Bài 5.10: PHƯƠNG PHÁP SINH MÃ XOAY VÒNG
Mục tiêu
Sau khi hoàn tất bài học này bạn có thể:
- Hiểu các phương pháp sinh mã vòng,
- Biết bảng liệt kê một số đa thức đặc trưng,
- Vận dụng để sinh mã vòng theo nhiều cách khách nhau.
Đặt vấn đề
Để sinh bộ mã kiểm tra chẵn lẻ, ta có thể dựa theo nhiều phương pháp khác nhau như: sinh mã
dựa theo lý thuyết nhóm, mã Hamming,... Vấn đề đặt ra ở đây là làm sao để sinh bộ mã xoay vòng
với độ dài n bit và m bit kiểm tra chẵn lẻ. Phương pháp sinh mã xoay vòng dựa trên lý thuyết về
đa thức đặc trưng nhị phân của thanh ghi giúp ta có cái nhìn tổng quát về vấn đề sinh bộ mã xoay
vòng theo nhiều cách khác nhau.
Phương pháp sinh bảng mã xoay vòng
Để sinh mã xoay vòng độ dài n bit với m bit kiểm tra và k bit thông tin, ta có thể thực hiện theo
các bước sau:
2 m-1 m
Bước 1: tìm 2 đa thức gm(x)=a0 + a1x+ a2 x + +am-1x + x
2 k-1 k n
và hk(x)=h0 + h1x+ h2x + +hk-1x + x sao cho (x + 1) = gm(x)* hk(x).
n
Nếu ∃ (x + 1) = gm(x)* hk(x) thì chuyển sang bước 2
Ngược lại không thể sinh bộ mã vòng theo yêu cầu.
Bước 2: ta có thể sinh bộ mã xoay vòng theo các cách như dưới đây:
2 m-1 m
Cách 1: Chọn đa thức gm(x)=a0 + a1x+ a2 x + +am-1x + x
⇒ a0, a1, a2,, am-1
⇒ thanh ghi ⇒ ma trận đặc trưng T
⇒ chu kỳ n ⇒ ma trận kiểm tra chẵn lẻ A.
⇒ Bộ mã xoay vòng.
2 m-1 m
Cách 2: chọn đa thức gm(x)=a0 + a1x+ a2 x + +am-1x + x
⇒ a0, a1, a2,, am-1
⇒ Sinh nhanh k từ mã độc lập tuyến tính với từ mã sinh độc lập tuyến tính đầu tiên có
dạng: w1=a0a1a2am-1100000 ⇒ Bộ mã xoay vòng.
k-1 bit 0
2 k-1 k
Cách 3: chọn hk(x)=h0 + h1x+ h2x + +hk-1x + x làm đa thức sinh ma trận kiểm tra
chẵn lẻ cho bộ mã vòng có dạng:
⎛ 0 0 − − − 0 0 1 h − − − h h ⎞
⎜ k −1 1 0 ⎟
⎜ 0 − − − 0 0 1 hk −1 − − − h1 h0 0 ⎟
⎜− − − − − − − − − − − − − − ⎟ m
⎜ ⎟
⎜ 0 1 kk −1 − − − h1 h0 0 0 − − − 0 ⎟
⎜ ⎟
⎝ 1 hk −1 − − − h1 h0 0 0 − − − 0 0 ⎠
(m-1) bits
⇒ Sinh bộ mã xoay vòng theo Phương pháp sinh nhanh bộ mã xoay vòng.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 88
Giáo trình: Lý thuyết thông tin.
Nhận xét: kết quả theo 3 cách sinh bộ mã xoay vòng nói trên la như nhau (cho cùng bộ mã).
Ví dụ minh họa 1
Thiết kế thanh ghi và sinh ma trận kiểm tra chẵn lẻ.
Chọn đa thức gm(x)= 1+x+x4 ⇒ a0 = 1, a1 = 1, a2 = 0, a3 = 0
+ F3 F2 F1 F0
⎡0 1 0 0⎤
⎢0 0 1 0⎥
Ma trận đặc trưng của thanh ghi: T= ⎢ ⎥
⎢0 0 0 1⎥
⎢ ⎥
⎣1 1 0 0⎦
Tìm chu kỳ của thanh ghi:
⎛0⎞
⎜ ⎟
⎜0⎟
Chọn giá trị khởi tạo x(0)=1=
⎜0⎟
⎜ ⎟
⎜ ⎟
⎝1⎠
⎛0⎞ ⎛0⎞ ⎛1⎞ ⎛0⎞ ⎛0⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜0⎟ ⎜1⎟ ⎜0⎟ ⎜0⎟ ⎜1⎟
x(1)=T.x(0)= ; x(2)=Tx(1)= ; x(3)=Tx(2)= ; x(4)=Tx(3)= ; x(5)=Tx(4)=
⎜1⎟ ⎜0⎟ ⎜0⎟ ⎜1⎟ ⎜1⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝0⎠ ⎝0⎠ ⎝1⎠ ⎝1⎠ ⎝0⎠
⎛1⎞ ⎛1⎞ ⎛0⎞ ⎛1⎞ ⎛0⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜1⎟ ⎜0⎟ ⎜1⎟ ⎜0⎟ ⎜1⎟
x(6)=Tx(5)= ; x(7)=Tx(6)= ; x(8)=Tx(7)= ; x(9)=Tx(8)= ; x(10)=Tx(9)=
⎜0⎟ ⎜1⎟ ⎜0⎟ ⎜1⎟ ⎜1⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝1⎠ ⎝0⎠ ⎝1⎠ ⎝1⎠ ⎝1⎠
⎛1⎞ ⎛1⎞ ⎛1⎞ ⎛1⎞ ⎛0⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜1⎟ ⎜1⎟ ⎜1⎟ ⎜0⎟ ⎜0⎟
x(11)=Tx(12)= ;x(12)=Tx(11)= ;x(13)=Tx(12)= ;x(14)=Tx(13)= ; x(15)=T.x(14) = = x(0)
⎜1⎟ ⎜1⎟ ⎜0⎟ ⎜0⎟ ⎜0⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎝1⎠ ⎝0⎠ ⎝0⎠ ⎝0⎠ ⎝1⎠
Ma trận kiểm tra chẳn lẻ :
⎛0 0 0 1 0 0 1 1 0 1 0 1 1 1 1⎞
⎜ ⎟
⎜0 0 1 0 0 1 1 0 1 0 1 1 1 1 0⎟
A=
⎜0 1 0 0 1 1 0 1 0 1 1 1 1 0 0⎟
⎜ ⎟
⎜ ⎟
⎝1 0 0 1 1 0 1 0 1 1 1 1 0 0 0⎠
⇒ Bộ mã xoay vòng vớin=14, m=4, k=11.
Ví dụ minh họa 2
Chọn đa thức gm(x)= 1+x+x4 ⇒ a0 = 1, a1 = 1, a2 = 0, a3 = 0.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 89
Giáo trình: Lý thuyết thông tin.
Bước 1: Sinh mã xoay vòng đầu tiên
w1 =110010000000000
Bước 2: Sinh k -1 từ mã độc lập tuyến tính còn lại
w2 =011001000000000
w3 =001100100000000
w4 =000110010000000
w5 =000011001000000
w6 =000001100100000
w7 =000000110010000
w8 =000000011001000
w9 =000000001100100
w10=000000000110010
w11=000000000011001
Bước 3: Xác định các từ mã còn lại của bộ mã
(215 - 11) từ mã còn lại được xác định bằng cách cộng tổ hợp 2, 3, 4,.., k = 11 từ
mã từ k=11 từ mã độc lập tuyến tính.
Ví dụ minh họa 3
2 3 5 7 8 11
Chọn hk(x)= 1+ x + x + x +x + x + x + x làm đa thức sinh ma trận kiểm tra chẵn lẻ cho bộ mã
vòng ⇒ h0 = 1, h1 = 1, h2 = 1, h3 = 1, h4 = 0, h5 = 1, h6 = 0, h7 = 1, h8 =1, h9 = 0, h10 = 0.
⎛0 0 0 1 0 0 1 1 0 1 0 1 1 1 1⎞
⎜ ⎟
⎜0 0 1 0 0 1 1 0 1 0 1 1 1 1 0⎟
A= ⇒ Bộ mã xoay vòng
⎜0 1 0 0 1 1 0 1 0 1 1 1 1 0 0⎟
⎜ ⎟
⎜ ⎟
⎝1 0 0 1 1 0 1 0 1 1 1 1 0 0 0⎠
Bảng liệt kê một số đa thức đặc trưng
M Đa thức M Đa thức
3 1+x+x3 14 1+x+x6+x10+x14
4 1+x+x4 15 1+x+x15
5 1+x2+x5 16 1+x+x3+x12+x16
6 1+x+x6 17 1+x3+x7
7 1+x3+x7 18 1+x7+x18
8 1+x2+x3+x4+x8 19 1+x+x2+x5+x19
9 1+x4+x9 20 1+x3+x20
10 1+x3+x10 21 1+x2+x21
11 1+x2+x11 22 1+x+x22
12 1+x+x4+x6+x12 23 1+x3+x23
13 1+x+x3+x4+x13 24 1+x+x2+x7+x24
Bài tập
1. Tìm bộ mã vòng có độ dài 7 bit.
2. Tìm thanh ghi sinh bộ mã vòng có độ dài 15 bit.
3. Tìm thanh ghi sinh bộ mã vòng có độ dài 31 bit.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 90
Giáo trình: Lý thuyết thông tin.
BÀI TẬP TỔNG HỢP
Mục tiêu
Sau khi hoàn tất bài học này bạn có thể:
- Hiểu rõ hơn về nội dung môn học.
- Vận dụng nội dung môn học để giải quyết một số bài tập tổng hợp.
Bài 1
Xét một mô hình chẩn đoán bệnh từ các triệu chứng: A, B và C; để chẩn đoán 1 trong 4 bệnh: 1,
2, 3 và 4 với ma trận chẩn đoán (hay ma trận truyền tin).
Bệnh 1 2 3 4
Triệu chứng
A 0,6 0,3 0 0,1
B 0,2 0,6 0,2 0
C 0 0 0,3 0,7
Yêu cầu:
Câu 1: Vẽ sơ đồ mô tả mô hình chẩn đoán bệnh trên và diễn giải các ý nghĩa của sơ đồ.
Câu 2: Nếu phân phối của Triệu chứng có dạng:
Triệu chứng A B C
P 0,5 0,3 0,2
Tính các lượng sau :
¾ Lượng ngẫu nhiên (Entropy) của Triệu chứng .
¾ Lượng ngẫu nhiên của Bệnh.
¾ Lượng ngẫu nhiên của Bệnh khi biết Triệu chứng.
¾ Lượng chẩn đoán đúng.(Lượng thông tin biết về Bệnh thông qua Triệu chứng) và tỷ lệ
chẩn đoán đúng là bao nhiêu phần trăm.
Câu 3: Bây giờ người ta sử dụng 2 bit để mã thông tin về Triệu chứng (có 1 triệu chứng dự trữ) và
5 bit để mã các triệu chứng khi chẩn đoán bệnh trực tuyến. Mô tả các đoạn của dãy 5 bit trong
phương pháp kiểm tra chẵn lẻ.
Câu 4: Nếu sử dụng ma trận kiểm tra chẵn lẻ dạng:
1 1 1 0 1
A = 0 1 0 1 1
1 0 0 1 1
Tính các từ mã.
Xây dựng Bộ sửa lỗi 1 bit dùng cho tự động sửa lỗi tối ưu trong quá trình chẩn đoán trực tuyến.
Cho một ví dụ.
Bài 2
Xét một kênh truyền tin đặc biệt dạng : Truyền X Æ Nhận Y.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 91
Giáo trình: Lý thuyết thông tin.
Truyền một giá trị của X có thể nhận được nhiều giá trị khác nhau của Y với các xác suất khác
nhau. Bảng xác suất truyền X và nhận các Y khác nhau được cho dưới đây:
Y y1 y2 y3 y4 y5 y6
X
x0 0,6 0,1 0,1 0,05 0,05 0,1
x1 0,1 0,05 0,6 0,1 0,1 0,05
x2 0,05 0,1 0,1 0,05 0,6 0,1
x3 0,1 0,05 0,05 0,1 0,1 0,6
Yêu cầu:
Câu 1: Vẽ sơ đồ mô tả kênh truyền tin trên và diễn giải các ý nghĩa của sơ đồ.
Câu 2: Nếu phân phối của X có dạng :
X x0 x1 x3 x4
P 0.5 0.25 0.15 0.1
tính thông lượng về X truyền trên kênh.
Câu 3: Phân phối của X cần có dạng như thế nào để thông lượng truyền trên kênh là lớn nhất.
Tính dung lượng kênh truyền.
Câu 4: Bây giờ người ta sử dụng 2 bit để mã thông tin về X và 4 bit để mã các giá trị truyền trên
kênh. Mô tả các đoạn của dãy 4 bit trong phương pháp kiểm tra chẵn lẻ.
Câu 5: Nếu sử dụng ma trận kiểm tra chẵn lẻ dạng:
1 1 1 0
A =
0 1 0 1
Tính các từ mã.
Xây dựng Bộ sửa lỗi dùng cho tự động sửa lỗi tối ưu trong quá trình truyền tin. Cho một ví dụ.
Bài 3
Người ta cần đánh giá kênh truyền tin và chuẩn bị thực hiện truyền một loại tín hiệu đặc biệt: X =
{x0, x1, x2, x3}
Công việc đầu tiên là phải khảo sát kênh truyền. Kết quả khảo sát cho thấy:
Kênh có thể truyền nhận được 8 giá trị khác nhau, để có khả năng phát hiện lỗi hoặc điều chỉnh
lỗi. Ma trận truyền tin có dạng:
Y y1 y2 y3 y4 y5 y6 y7 y8
X
x0 0,6 0,1 0,05 0,05 0,05 0,05 0,05 0,05
x1 0,05 0,05 0,6 0,1 0,05 0,05 0,05 0,05
x2 0,05 0,05 0,05 0,05 0,6 0,1 0,05 0,05
x3 0,05 0,05 0,05 0,05 0,05 0,05 0,6 0,1
Yêu cầu:
Câu 1: Vẽ sơ đồ mô tả kênh truyền tin trên và diễn giải các ý nghĩa của sơ đồ. Nếu phân phối của
X có dạng :
X x0 x1 x3 x4
P 0.5 0.25 0.15 0.1
tính thông lượng về X truyền trên kênh.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 92
Giáo trình: Lý thuyết thông tin.
Câu 2: Phân lớp các giá trị của Y về các lớp B0, B1, B2, và B3 dùng để giải mã tối ưu Y tốt nhất
về các giá trị tương ứng của X.
Câu 3 : Bây giờ người ta sử dụng 2 bit để mã thông tin về X và 4 bit để mã các giá trị truyền trên
kênh. Mô tả các đoạn của dãy 4 bit trong phương pháp kiểm tra chẵn lẻ.
Câu 4: Nếu sử dụng ma trận kiểm tra chẵn lẻ dạng:
1 0 0 1
A = 0 1 1 1
Tính các từ mã.
Xây dựng Bộ sửa lỗi dùng cho tự động sửa lỗi tối ưu trong quá trình truyền tin. Cho một ví dụ.
Bài 4
Xét một mô hình chẩn đoán bệnh từ các triệu chứng: A, B và C; để chẩn đoán 1 trong 4 bệnh: 1,
2, 3 và 4 với ma trận chẩn đoán (hay ma trận truyền tin)
Bệnh 1 2 3 4
Triệu chứng
A 0,5 0,3 0 0,2
B 0,1 0,2 0,7 0
C 0 0,1 0,3 0,6
Yêu cầu:
Câu 1: Giả sử người ta biết thêm 3 triệu chứng gây bệnh khác đó là : D, E và F và muốn ghi lại
các triệu chứng này thông qua bảng ký hiệu A = {+, - }.
Hãy kiểm tra tính tách được của bảng mã sau :
Triệu chứng : X A B C D E F
Mã : W + -+ ++- --+- ++-+ --
Câu 2: Nếu các triệu chứng ở câu 1 có phân phối :
Triệu chứng : X A B C D E F
P 0.5 0.2 0.2 0.05 0.03 0.2
Giử sử có một người bệnh với 1 trong 5 triệu chứng trên đến khám bệnh và bác sĩ sẽ hỏi bệnh với
nguyên tắc, sao cho người bệnh chỉ trả lời bằng 2 câu : Đúng hoặc Sai.
¾ Tìm phương pháp hỏi bệnh với số câu hỏi trung bình ít nhất.
¾ Tính số câu hỏi trung bình.
¾ Tính lượng ngẫu nhiên của Triệu chứng.
¾ Nhận xét gì về số câu hỏi trung bình và lượng ngẫu nhiên của triệu chứng.
Câu 3: Bây giờ sử dụng mô hình 3 triệu chứng {A, B, C} và 4 bệnh. Vẽ sơ đồ mô tả mô hình
chẩn đoán bệnh và diễn giải các ý nghĩa của sơ đồ.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 93
Giáo trình: Lý thuyết thông tin.
Câu 4: Từ kết quả câu 3, người ta sử dụng 2 bit để mã thông tin về Triệu chứng (có 1 triệu chứng
dự trữ) và 5 bit để mã các triệu chứng khi chẩn đoán bệnh trực tuyến. Mô tả các đoạn của dãy 5
bit trong phương pháp kiểm tra chẵn lẻ.
Câu 5: Nếu sử dụng ma trận kiểm tra chẵn lẻ dạng:
1 1 1 0 1
A = 0 1 0 1 1
1 0 0 1 1
Tính các từ mã.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 94
Giáo trình: Lý thuyết thông tin.
TÀI LIỆU THAM KHẢO
12. G.J.ChaiTin, Algorithmic Information Theory, CamBridge University Express-1992.
13. David J.C. Mackey, Information Theory, Infernce, and Learning Algorithms, CamBridge
University Express-2003.
14. Sanford Goldman, Information Theory.
15.
16.
17.
18.
19.
20.
21.
22.
Biên soạn: TS. L ê Quy ết Thắng, ThS. Phan Tấn Tài & Ks. Dương Văn Hiếu. 95File đính kèm:
 giao_trinh_ly_thuyet_thong_tin.pdf
giao_trinh_ly_thuyet_thong_tin.pdf

