Electrocardiography signal denoising using translation invariant wavelet threshold algorithm

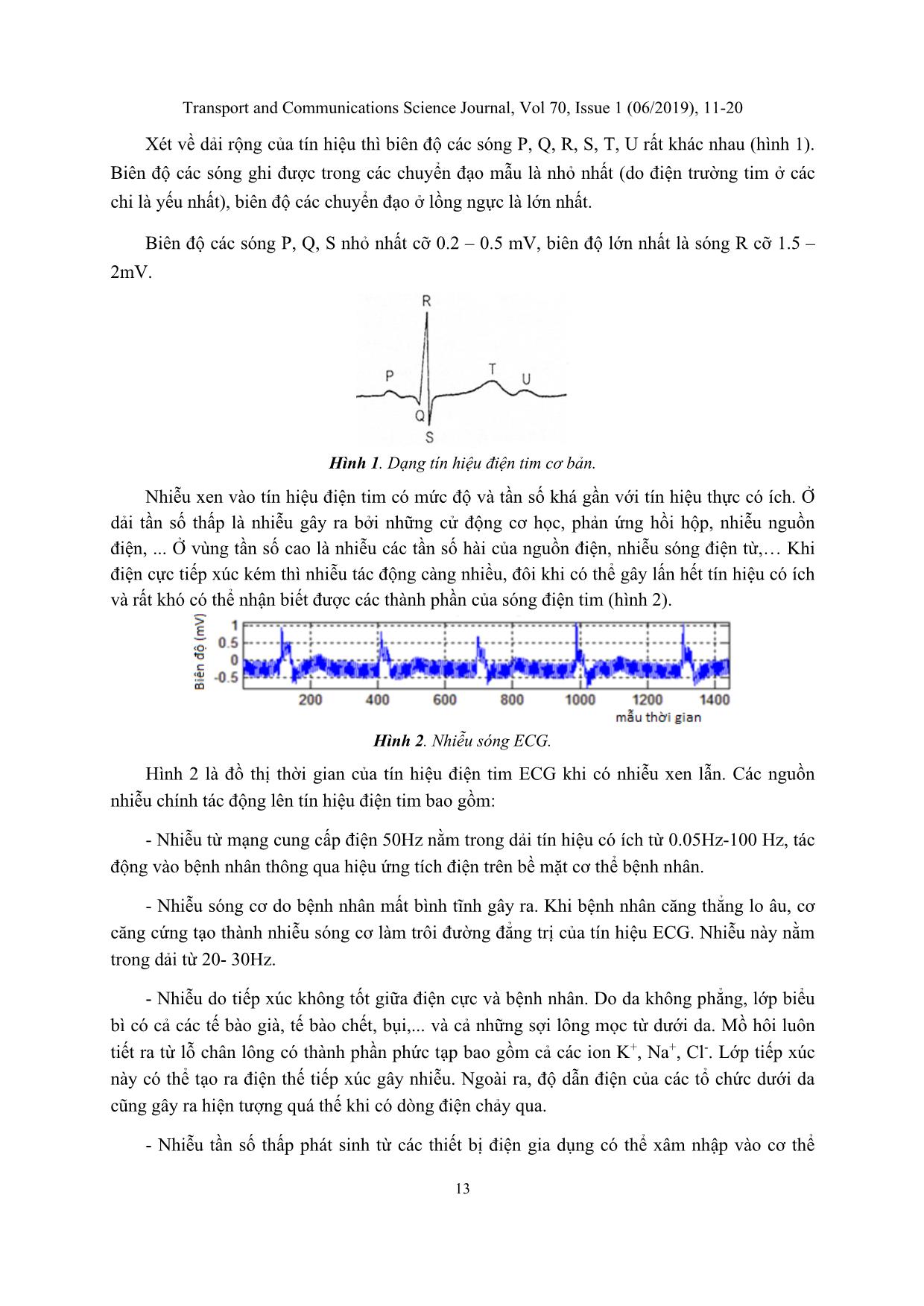
. Ở vùng tần số cao là nhiễu các tần số hài của nguồn điện, nhiễu sóng điện từ, Khi 
điện cực tiếp xúc kém thì nhiễu tác động càng nhiều, đôi khi có thể gây lấn hết tín hiệu có ích 
và rất khó có thể nhận biết được các thành phần của sóng điện tim (hình 2). 
Hình 2. Nhiễu sóng ECG. 
Hình 2 là đồ thị thời gian của tín hiệu điện tim ECG khi có nhiễu xen lẫn. Các nguồn 
nhiễu chính tác động lên tín hiệu điện tim bao gồm: 
- Nhiễu từ mạng cung cấp điện 50Hz nằm trong dải tín hiệu có ích từ 0.05Hz-100 Hz, tác 
động vào bệnh nhân thông qua hiệu ứng tích điện trên bề mặt cơ thể bệnh nhân. 
- Nhiễu sóng cơ do bệnh nhân mất bình tĩnh gây ra. Khi bệnh nhân căng thẳng lo âu, cơ 
căng cứng tạo thành nhiễu sóng cơ làm trôi đường đẳng trị của tín hiệu ECG. Nhiễu này nằm 
trong dải từ 20- 30Hz. 
- Nhiễu do tiếp xúc không tốt giữa điện cực và bệnh nhân. Do da không phẳng, lớp biểu 
bì có cả các tế bào già, tế bào chết, bụi,... và cả những sợi lông mọc từ dưới da. Mồ hôi luôn 
tiết ra từ lỗ chân lông có thành phần phức tạp bao gồm cả các ion K+, Na+, Cl-. Lớp tiếp xúc 
này có thể tạo ra điện thế tiếp xúc gây nhiễu. Ngoài ra, độ dẫn điện của các tổ chức dưới da 
cũng gây ra hiện tượng quá thế khi có dòng điện chảy qua. 
- Nhiễu tần số thấp phát sinh từ các thiết bị điện gia dụng có thể xâm nhập vào cơ thể 
Tạp chí Khoa học Giao thông vận tải, Tập 70, Số 1 (06/2019), 11-20 
14 
theo hiệu ứng cảm ứng từ trường, tần số càng thấp thì xâm nhập càng sâu. Nhiễu này có thể 
làm trôi đường nền tín hiệu. 
- Nhiễu tần số cao gây bởi các thiết bị thu phát điện tử như tivi, radio, điện thoại,Nhiễu 
này xen vào nền các sóng điện tim cơ bản gây méo tín hiệu. 
Việc khử nhiễu tín hiệu điện tim để đưa ra được tín hiệu trung thực, giúp bác sỹ chẩn 
đoán chính xác các bệnh lý theo điện tâm đồ luôn được thực hiện trong các thiết bị và trên các 
phương tiện phân tích điện tâm đồ. Biến đổi wavelet là một phương pháp toán học được nhiều 
nhà khoa học, các nhà chuyên môn nghiên cứu và thực hiện. Các biện pháp khử nhiễu sử 
dụng biến đổi wavelet rời rạc DWT [2] [3] có hiệu quả khử nhiễu khá tốt, nhưng trong một số 
trường hợp có thể sinh ra một số dao động giả tạo do quá trình biến đổi. Một số nghiên cứu 
phương pháp khử nhiễu sử dụng biến đổi wavelet dịch bất biến TIDWT (Translation-Invariant 
Discrete Wavelet transforms) [4] đã công bố sử dụng ngưỡng phổ dụng (ngưỡng đều), tín hiệu 
khôi phục trơn hơn DWT (Discrete Wavelet transforms), nhưng chỉ ứng dụng tốt trong các 
môi trường chuẩn, nhiễu trắng. Giải thuật khử nhiễu đề xuất trong bài báo có thể ứng dụng 
trong môi trường nhiễu phức tạp hơn. Giải thuật thực hiện trên cơ sở TIDWT, ước lượng tất 
cả các dịch của tín hiệu và lấy trung bình sau mỗi lần dịch ngược. Do không thực hiện bước 
phân chia khi biến đổi nên TIDWT giữ lại được nhiều thành phần tín hiệu, tín hiệu khôi phục 
sẽ trung thực hơn. Dịch bất biến nên khi ước lượng khử nhiễu, ngoài nhiễu không tương quan, 
giải thuật mới có thể loại bỏ được cả các loại nhiễu tương quan [1]. 
II. BIẾN ĐỔI WAVELET DỊCH BẤT BIẾN TIDWT 
1. Biến đổi wavelet rời rạc dịch bất biến TIDWT 
Biến đổi wavelet rời rạc DWT vec tơ x RN thông qua phép biến đổi hình chóp cho ma 
trận vuông W trực giao N x N, biến đổi ngược cho ma trận WT. Giải thuật hình chóp bao gồm 
cả lấy mẫu xuống ở từng tỷ lệ. Biến đổi wavelet rời rạc dịch bất biến TIDWT không thực hiện 
lấy mẫu xuống ở mỗi tỷ lệ mà tính toán tất cả các hệ số dịch vì vậy giữ lại tất cả các hệ số 
wavelet và các hệ số tỷ lệ ở các tỷ lệ thô. 
Ở tỷ lệ j ≤ log2N, các hệ số tỷ lệ (hệ số xấp xỉ) là vec tơ: 
 𝒄(𝑗) = (𝑐1
(𝑗),  , 𝑐𝑁
(𝑗)) (1) 
 𝑐𝑘
(𝑗) = ∑ ℎ𝑙𝑐𝑘+2𝑗−𝑙
(𝑗−𝑙)
𝑙∈𝑧 (2) 
và các hệ số wavelet (hệ số chi tiết) là các vec tơ: 
 𝒅(𝑗) = (𝑑1
(𝑗),  , 𝑑𝑁
(𝑗)) (3) 
 𝑑𝑘
(𝑗) = ∑ 𝑔𝑙𝑑𝑘+2𝑗−𝑙
(𝑗−𝑙)
𝑙∈𝑧 (4) 
Transport and Communications Science Journal, Vol 70, Issue 1 (06/2019), 11-20 
15 
TIDWT cho ma trận ML kích thước (L+1)N x N, trong đó L là mức khai triển cực đại. 
Gọi ma trận Ri kích thước N x N là ma trận các hệ số wavelet ở tỷ lệ thứ j, nghĩa là Rj(x) 
= d(j) và ma trận Si gồm các hệ số tỷ lệ ở tỷ lệ thứ j, nghĩa là Si(x) = c(j) thì: 
 𝑀𝐿 = (𝑅1
𝑇,  , 𝑅𝐿
𝑇 , 𝑆𝐿
𝑇)𝑇 (5) 
Như vậy, ma trận ML không trực giao như biến đổi wavelet rời rạc DWT. Theo lý thuyết 
ma trận, tồn tại ma trận đảo Moore-Penrose: 
 𝑀𝐿
𝑡 = (𝑀𝐿
𝑇𝑀𝐿)
−1𝑀𝐿
𝑇 (6) 
thỏa mãn: 𝑀𝐿
𝑡𝑀𝐿 = 𝐼. 
ML gồm tất cả các dịch của ma trận hệ số biến đổi wavelet rời rạc W nên dạng hiện của 
ma trận 𝑀𝐿
𝑡 sẽ là: 
 𝑀𝐿
𝑡 = (
1
2
𝑅1
𝑇 ,  ,
1
2𝐿
𝑅𝐿
𝑇 ,
1
2𝐿
𝑆𝐿
𝑇) (7) 
Điều này chứng tỏ rằng biến đổi ngược wavelet rời rạc dịch bất biến lấy trung bình qua 
tất cả các dịch của biến đổi wavelet rời rạc. 
Các ma trận Ri và Si có thể tính được từ cách tính các bộ lọc tự tương quan (bộ lọc à-
trous) a = {ak:k Z); a2k = 0k: 
 𝑎𝑘 = ∑ ℎ𝑙ℎ𝑙+𝑘𝑙 (8) 
 𝑏𝑘 = ∑ 𝑔𝑙𝑔𝑙+𝑘𝑙 (9) 
Xác định các ma trận tỷ lệ Ti và ma trận Qi: 
 𝑇𝑗 = 2
−𝑗𝑆𝑗
𝑇𝑆𝑗 (10) 
 𝑄𝑗 = 2
−𝑗𝑅𝑗
𝑇𝑅𝑗 (11) 
Trong đó, các phần tử ma trận Ti(x) là: 
 𝑡𝑗,𝑘(𝑥) = ∑ 𝑎𝑚1  𝑎𝑚𝑗𝑥𝑘+𝑚1+⋯+2𝑗𝑚𝑗𝑚1,,𝑚𝑗 , với x = {xi} (12) 
Bằng cách nhân ma trận TL với tập dữ liệu vào x ta được hình chiếu dịch bất biến của x. 
Các hình chiếu này đóng vai trò quan trọng trong đặc tính trơn của các hàm khử nhiễu dịch 
bất biến. 
Các tập a và b là các bộ lọc tự tương quan của các bộ lọc wavelet h và g với các quan hệ: 
gk = (-l)
khl-k và bk = (-l)
kak. 
Các bộ lọc wavelet thực hiện trong các hàm tỷ lệ và wavelet còn các giá trị ak và bk là các 
hệ số trong các biểu thức quan hệ của các hàm tự tương quan  và : 
Tạp chí Khoa học Giao thông vận tải, Tập 70, Số 1 (06/2019), 11-20 
16 
(𝑠) = ∫ 𝜑(𝑥)𝜑(𝑥 + 𝑠)𝑑𝑥
+∞
−∞
 (13) 
(𝑠) = ∫ 𝜓(𝑥)𝜓(𝑥 + 𝑠)𝑑𝑥
+∞
−∞
 (14)
có các quan hệ: 
 (𝑥) = ∑ 𝑎𝑘(2𝑥 − 𝑘)𝑘∈𝑍 (15) 
 (𝑠) = ∑ (−1)𝑘𝑎𝑘(2𝑥 − 𝑘)𝑘∈𝑍 (16) 
Thực hiện TIDWT thông qua các bộ lọc thông thấp và thông cao khi biến đổi thuận và 
biến đổi ngược. 
2. Ước lượng ngưỡng wavelet 
Tín hiệu X sau biến đổi wavelet gồm tín hiệu gốc F và nhiễu W: 
 𝑋 = 𝐹 + 𝑊 (17) 
Giải thuật thực hiện ước lượng tất cả các dịch của X và lấy trung bình sau mỗi lần dịch 
ngược. 
Với 0 ≤ p < N, giá trị ước lượng của tín hiệu 𝐹𝑝được tính bằng thuật ngưỡng dữ liệu 
dịch 𝑋𝑝[𝑛] = 𝑋[𝑛 − 𝑝] trong tập cơ sở B = {gm}0≤m<N, 𝑋𝐵[𝑚] = 〈𝑋, 𝑔𝑚〉: 
 𝐹𝑝 = ∑ 𝜌Γ
𝑁−1
𝑚=0 (𝑋𝐵
𝑃[𝑚])𝑔𝑚 (18) 
Trong đó, 𝜌Γ(𝑥) là hàm ngưỡng, có thể sử dụng ngưỡng cứng hoặc ngưỡng mềm [2] [3]. 
Ước lượng dịch bất biến có được bằng cách dịch ngược và lấy trung bình các ước lượng: 
 �̃�[𝑛] =
1
𝑁
∑ 𝐹𝑝[𝑛 + 𝑝]𝑁−1𝑝=0 (19) 
Giá trị ngưỡng tại tỷ lệ (mức biến đổi) thứ j (1 < j ≤ L) được xác định bao gồm các thành 
phần nhiễu không tương quan và nhiễu tương quan [1]: 
 𝑢𝑗 = 𝑗j√2(1 + ) log(𝐿 + 1) 𝑁 (20) 
Trong đó, L là mức biến đổi wavelet cực đại,  là giá trị xác định từ tương quan chéo hay 
hợp biến các hệ số biến đổi wavelet dịch xivà xm: 
  = max (𝑐𝑜𝑣(𝑥𝑖, 𝑥𝑚)) (21) 
Giá trị j từ đặc tính phân bố nhiễu không tương quan, được tính theo hệ số chi tiết thứ k 
ở tỷ lệ thứ j: 
 𝜎𝜂𝑗 =
𝑚𝑒𝑑𝑖𝑎𝑛(|𝑑(𝑗,𝑘)|)
0.6745
 (22) 
Giá trị 𝑗ở mức biến đổi thứ j được xác định từ các giá trị phương sai nhiễu tương 
Transport and Communications Science Journal, Vol 70, Issue 1 (06/2019), 11-20 
17 
quan𝑗
2 là các thành phần đường chéo ma trận hợp biến biến đổi wavelet: 
 𝑗
2 = 𝑑𝑖𝑎𝑔(𝑀𝑗𝑀𝑗
𝑇) (23) 
Các bước chính thực hiện giải thuật như sau: 
- Biến đổi wavelet thuận tín hiệu bao gồm nhiễu để có được các hệ số wavelet. 
- Tính toán ngưỡng theo các công thức (23), (22), (21), (20). 
- Thực hiện ước lượng theo công thức (18), (19). 
- Biến đổi wavelet ngược, khôi phục tín hiệu. 
III. KẾT QUẢ KHỬ NHIỄU 
Giải thuật đã được mô phỏng trên Matlab, tính toán tỷ số tín hiệu trên nhiễu SNR (Signal 
to Noise Ratio) so sánh với giải thuật truyền thống sử dụng DWT trên tín hiệu có nhiễu mô 
phỏng. Giải thuật cũng được thực hiện với một số hàm wavelet khác nhau để kiểm chứng hiệu 
quả khử nhiễu. Khử nhiễu tín hiệu thực cũng được thực hiện và được đánh giá trực quan trên 
đồ thị. 
1. Khử nhiễu tín hiệu ECG nhiễu mô phỏng 
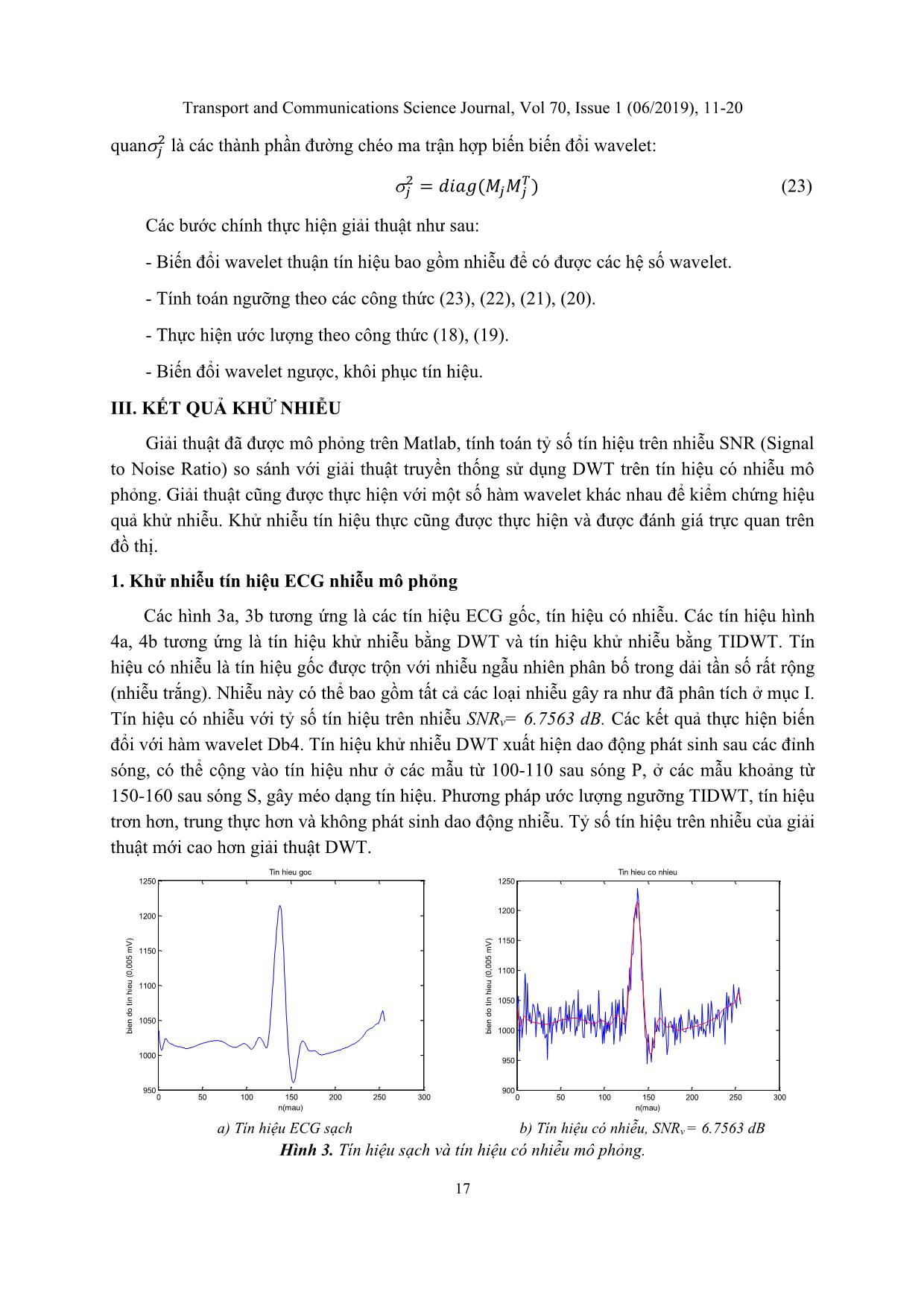
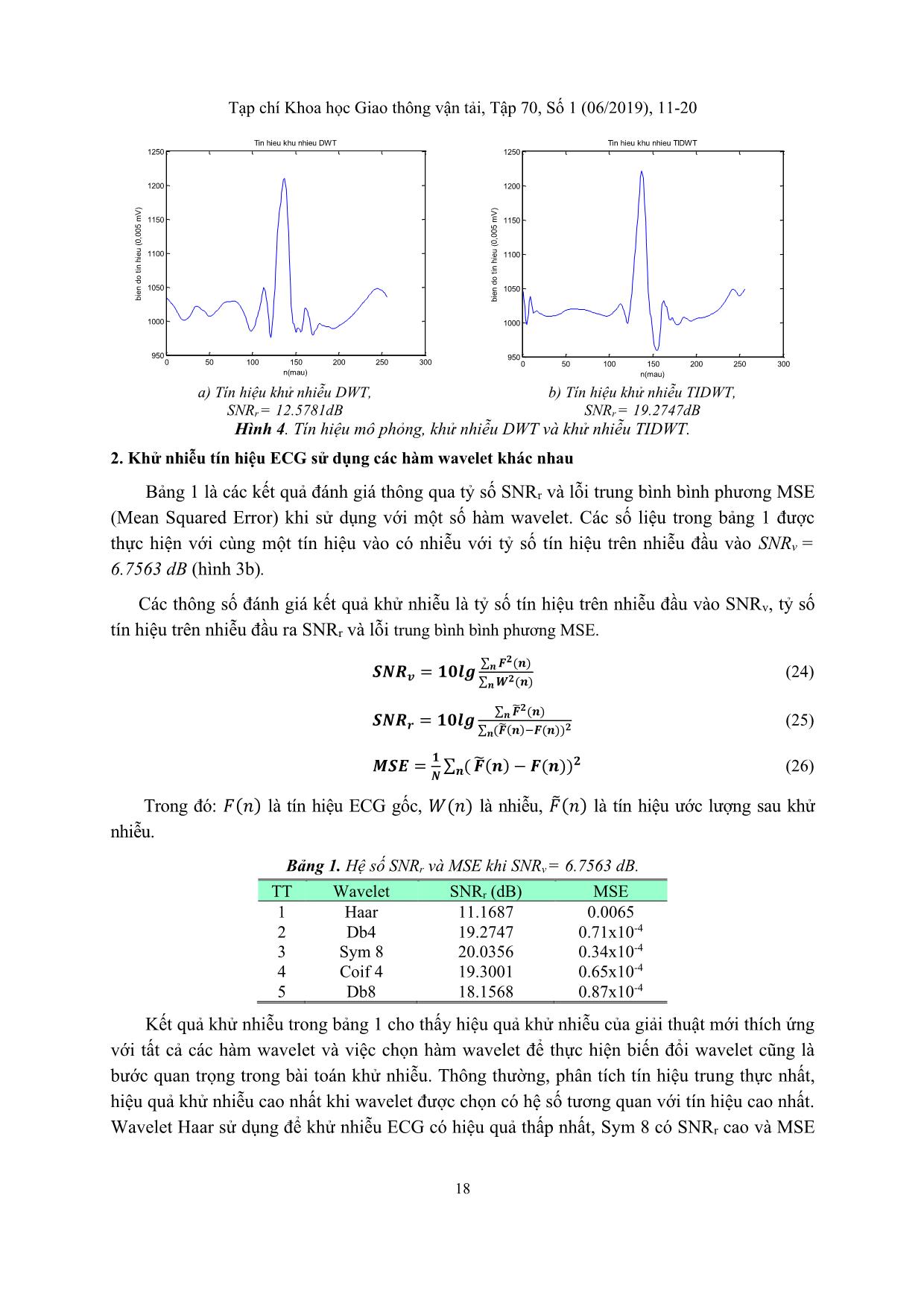
Các hình 3a, 3b tương ứng là các tín hiệu ECG gốc, tín hiệu có nhiễu. Các tín hiệu hình 
4a, 4b tương ứng là tín hiệu khử nhiễu bằng DWT và tín hiệu khử nhiễu bằng TIDWT. Tín 
hiệu có nhiễu là tín hiệu gốc được trộn với nhiễu ngẫu nhiên phân bố trong dải tần số rất rộng 
(nhiễu trắng). Nhiễu này có thể bao gồm tất cả các loại nhiễu gây ra như đã phân tích ở mục I. 
Tín hiệu có nhiễu với tỷ số tín hiệu trên nhiễu SNRv= 6.7563 dB. Các kết quả thực hiện biến 
đổi với hàm wavelet Db4. Tín hiệu khử nhiễu DWT xuất hiện dao động phát sinh sau các đỉnh 
sóng, có thể cộng vào tín hiệu như ở các mẫu từ 100-110 sau sóng P, ở các mẫu khoảng từ 
150-160 sau sóng S, gây méo dạng tín hiệu. Phương pháp ước lượng ngưỡng TIDWT, tín hiệu 
trơn hơn, trung thực hơn và không phát sinh dao động nhiễu. Tỷ số tín hiệu trên nhiễu của giải 
thuật mới cao hơn giải thuật DWT. 
a) Tín hiệu ECG sạch b) Tín hiệu có nhiễu, SNRv = 6.7563 dB 
Hình 3. Tín hiệu sạch và tín hiệu có nhiễu mô phỏng. 
0 50 100 150 200 250 300
950
1000
1050
1100
1150
1200
1250
Tin hieu goc
n(mau)
b
ie
n
 d
o
 t
in
 h
ie
u
 (
0
,0
0
5
 m
V
)
0 50 100 150 200 250 300
900
950
1000
1050
1100
1150
1200
1250
Tin hieu co nhieu
n(mau)
b
ie
n
 d
o
 t
in
 h
ie
u
 (
0
,0
0
5
 m
V
)
Tạp chí Khoa học Giao thông vận tải, Tập 70, Số 1 (06/2019), 11-20 
18 
a) Tín hiệu khử nhiễu DWT, 
SNRr = 12.5781dB 
b) Tín hiệu khử nhiễu TIDWT, 
SNRr = 19.2747dB 
Hình 4. Tín hiệu mô phỏng, khử nhiễu DWT và khử nhiễu TIDWT. 
2. Khử nhiễu tín hiệu ECG sử dụng các hàm wavelet khác nhau 
Bảng 1 là các kết quả đánh giá thông qua tỷ số SNRr và lỗi trung bình bình phương MSE 
(Mean Squared Error) khi sử dụng với một số hàm wavelet. Các số liệu trong bảng 1 được 
thực hiện với cùng một tín hiệu vào có nhiễu với tỷ số tín hiệu trên nhiễu đầu vào SNRv = 
6.7563 dB (hình 3b). 
Các thông số đánh giá kết quả khử nhiễu là tỷ số tín hiệu trên nhiễu đầu vào SNRv, tỷ số 
tín hiệu trên nhiễu đầu ra SNRr và lỗi trung bình bình phương MSE. 
 𝑺𝑵𝑹𝒗 = 𝟏𝟎𝒍𝒈
∑ 𝑭𝟐(𝒏)𝒏
∑ 𝑾𝟐(𝒏)𝒏
 (24) 
 𝑺𝑵𝑹𝒓 = 𝟏𝟎𝒍𝒈
∑ �̃�𝟐(𝒏)𝒏
∑ (𝒏 �̃�(𝒏)−𝑭(𝒏))𝟐
 (25) 
 𝑴𝑺𝑬 =
𝟏
𝑵
∑ (𝒏 �̃�(𝒏) − 𝑭(𝒏))
𝟐 (26) 
Trong đó: 𝐹(𝑛) là tín hiệu ECG gốc, 𝑊(𝑛) là nhiễu, �̃�(𝑛) là tín hiệu ước lượng sau khử 
nhiễu. 
Bảng 1. Hệ số SNRr và MSE khi SNRv = 6.7563 dB. 
TT Wavelet SNRr (dB) MSE 
1 Haar 11.1687 0.0065 
2 Db4 19.2747 0.71x10-4 
3 Sym 8 20.0356 0.34x10-4 
4 Coif 4 19.3001 0.65x10-4 
5 Db8 18.1568 0.87x10-4 
Kết quả khử nhiễu trong bảng 1 cho thấy hiệu quả khử nhiễu của giải thuật mới thích ứng 
với tất cả các hàm wavelet và việc chọn hàm wavelet để thực hiện biến đổi wavelet cũng là 
bước quan trọng trong bài toán khử nhiễu. Thông thường, phân tích tín hiệu trung thực nhất, 
hiệu quả khử nhiễu cao nhất khi wavelet được chọn có hệ số tương quan với tín hiệu cao nhất. 
Wavelet Haar sử dụng để khử nhiễu ECG có hiệu quả thấp nhất, Sym 8 có SNRr cao và MSE 
0 50 100 150 200 250 300
950
1000
1050
1100
1150
1200
1250
Tin hieu khu nhieu DWT
n(mau)
b
ie
n
 d
o
 t
in
 h
ie
u
 (
0
,0
0
5
 m
V
)
0 50 100 150 200 250 300
950
1000
1050
1100
1150
1200
1250
Tin hieu khu nhieu TIDWT
n(mau)
b
ie
n
 d
o
 t
in
 h
ie
u
 (
0
,0
0
5
 m
V
)
Transport and Communications Science Journal, Vol 70, Issue 1 (06/2019), 11-20 
19 
nhỏ nhất. 
Thực hiện khử nhiễu với tín hiệu có nhiễu lớn hơn SNRv = 2.2576 dB. 
Kết quả khử nhiễu trong bảng 2 ứng với các wavelet khác nhau cho giải thuật mới khi tín 
hiệu có nhiễu lớn hơn cho thấy tương đương như bảng 1. Wavelet Harr có hiệu quả khử nhiễu 
thấp nhất nên wavelet này ít được sử dụng cho thuật toán khử nhiễu tín hiệu điện tim. 
Bảng 2. Hệ số SNRr và MSE khi SNRv = 2.2576 dB. 
TT Wavelet SNRr (dB) MSE 
1 Haar 6.1598 0.0132 
2 Db4 14.0276 0.83x10-4 
3 Sym 8 16.1463 0.52x10-4 
4 Coif 4 15.4189 0.71x10-4 
5 Db8 14.7142 0.96x10-4 
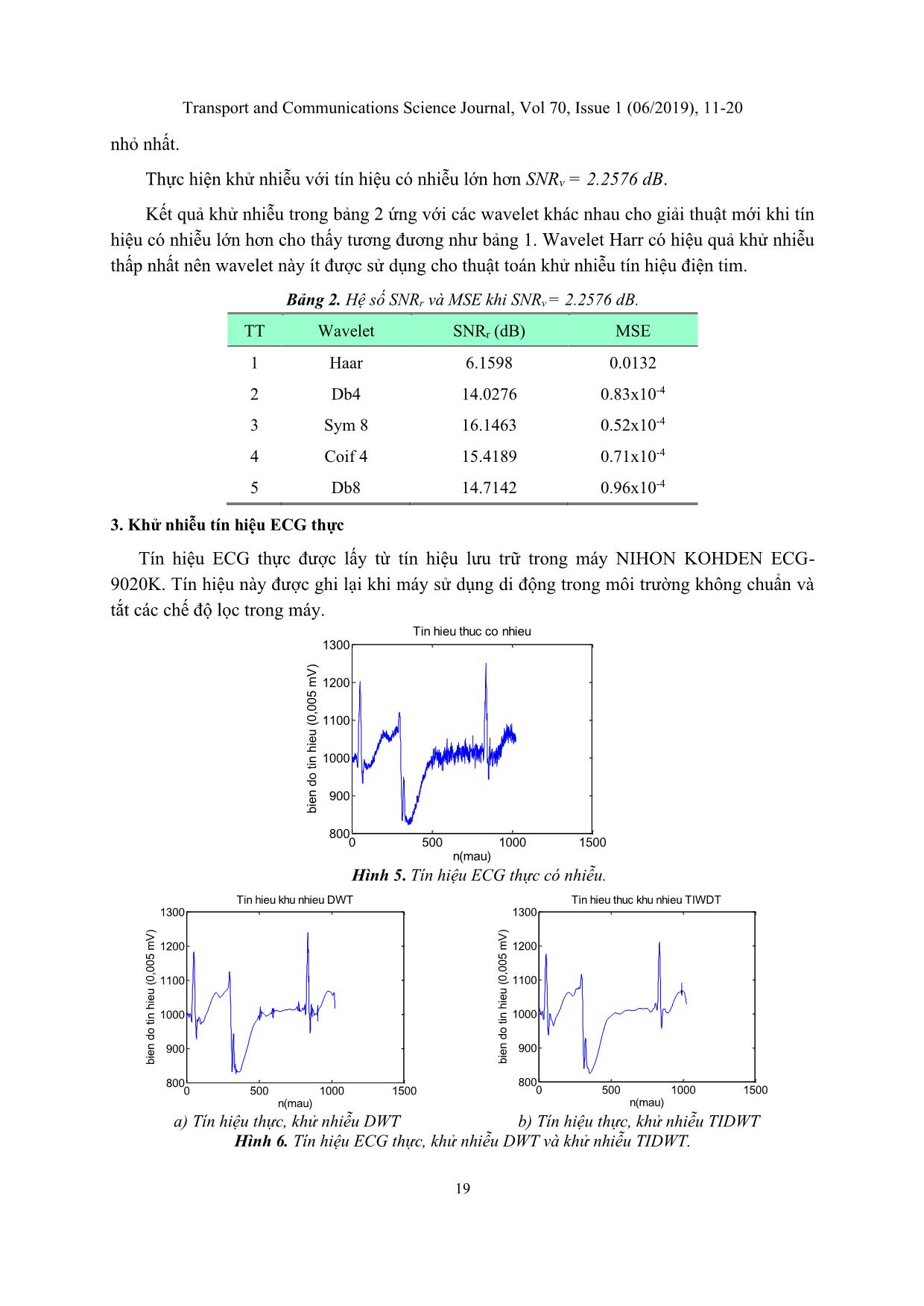
3. Khử nhiễu tín hiệu ECG thực 
Tín hiệu ECG thực được lấy từ tín hiệu lưu trữ trong máy NIHON KOHDEN ECG-
9020K. Tín hiệu này được ghi lại khi máy sử dụng di động trong môi trường không chuẩn và 
tắt các chế độ lọc trong máy. 
Hình 5. Tín hiệu ECG thực có nhiễu. 
a) Tín hiệu thực, khử nhiễu DWT b) Tín hiệu thực, khử nhiễu TIDWT 
Hình 6. Tín hiệu ECG thực, khử nhiễu DWT và khử nhiễu TIDWT. 
0 500 1000 1500
800
900
1000
1100
1200
1300
Tin hieu thuc co nhieu
n(mau)
b
ie
n
 d
o
 t
in
 h
ie
u
 (
0
,0
0
5
 m
V
)
0 500 1000 1500
800
900
1000
1100
1200
1300
Tin hieu khu nhieu DWT
n(mau)
b
ie
n
 d
o
 t
in
 h
ie
u
 (
0
,0
0
5
 m
V
)
0 500 1000 1500
800
900
1000
1100
1200
1300
Tin hieu thuc khu nhieu TIWDT
n(mau)
b
ie
n
 d
o
 t
in
 h
ie
u
 (
0
,0
0
5
 m
V
)
Tạp chí Khoa học Giao thông vận tải, Tập 70, Số 1 (06/2019), 11-20 
20 
Kết quả khử nhiễu tín hiệu thực trên hình 6a và hình 6b cho thấy tín hiệu khử nhiễu theo 
giải thuật mới trơn hơn và không xuất hiện các dao động nhiễu phát sinh. 
IV. KẾT LUẬN 
Khử nhiễu sử dụng biến đổi wavelet dịch bất biến TIDWT, giữ lại tất cả các hệ số 
wavelet thô, ước lượng dịch ngược, đề xuất trong nội dung bài báo đã đạt được một số cải 
thiện đặc tính khử nhiễu tín hiệu. Phương pháp TIDWT khắc phục được dao động phát sinh 
do quá trình biến đổi gây ra. Thuật toán ước lượng dịch bất biến trên tất cả các hệ số wavelet, 
đảm bảo làm trơn tín hiệu nhưng vẫn giữ lại được nhiều chi tiết tín hiệu có ích hơn, tín hiệu 
sau khử nhiễu trung thực hơn. Ngưỡng được tính đến các thông số của cả nhiễu tương quan và 
không tương quan nên có thể ứng dụng được trong những môi trường nhiễu phức tạp. 
TÀI LIỆU THAM KHẢO 
[1]. Đỗ Xuân Thiệu, Khử nhiễu tín hiệu bằng phương pháp ngưỡng phụ thuộc tương quan qua biến đổi 
wavelet, Tuyển tập các báo cáo khoa học Hội nghị toàn quốc về tự động hóa VICA6, Hà nội, ngày 14 
tháng 4 năm 2005, 478-483. 
[2]. Mounaim Aqil, Atman Jbari, Abdennasser Bourouhou, ECG signal Denoising by Discrete 
Wavelet Transform, International Journal of Online and Biomedical Engineering, 13 (2017) 51-68. 
https://doi.org/10.3991/ijoe.v13i09.7159 
[3]. Savita Chandel, Kuldeep Singh, ECG denoising using wavelet transform and soft thresholding, 
International Journal of Advanced Research in Computer Science and Software Engineering, 6 (2016) 
370. 
[4]. Zhidong Zhao, Mengjiao Lv, Xiaohong Zhang, Jiayou Du, Min Zheng. ECG De-noising Based on 
Translation Invariant Wavelet Transform and Overlapping Group Shrinkage, Sensors & Transducers, 
177 (2014) 54-62.