Efficient CNN - Based profiled side channel attacks
Profiled side-channel attacks are now considered as a powerful form of side channel
attacks used to break the security of cryptographic devices. A recent line of research has investigated
a new profiled attack based on deep learning and many of them have used convolution neural network
(CNN) as deep learning architecture for the attack. The effectiveness of the attack is greatly influenced
by the CNN architecture. However, the CNN architecture used for current profiled attacks have often
been based on image recognition fields, and choosing the right CNN architectures and parameters for
adaption to profiled attacks is still challenging. In this paper, we propose an efficient profiled attack
for unprotected and masking-protected cryptographic devices based on two CNN architectures, called
CNNn, CNNd respectively. Both of CNN architecture parameters proposed in this paper are based
on the property of points of interest on the power trace and further determined by the Grey Wolf
Optimization (GWO) algorithm. To verify the proposed attacks, experiments were performed on a
trace set collected from an Atmega8515 smart card when it performs AES-128 encryption, a DPA
contest v4 dataset and the ASCAD public dataset.

Trang 1

Trang 2

Trang 3

Trang 4
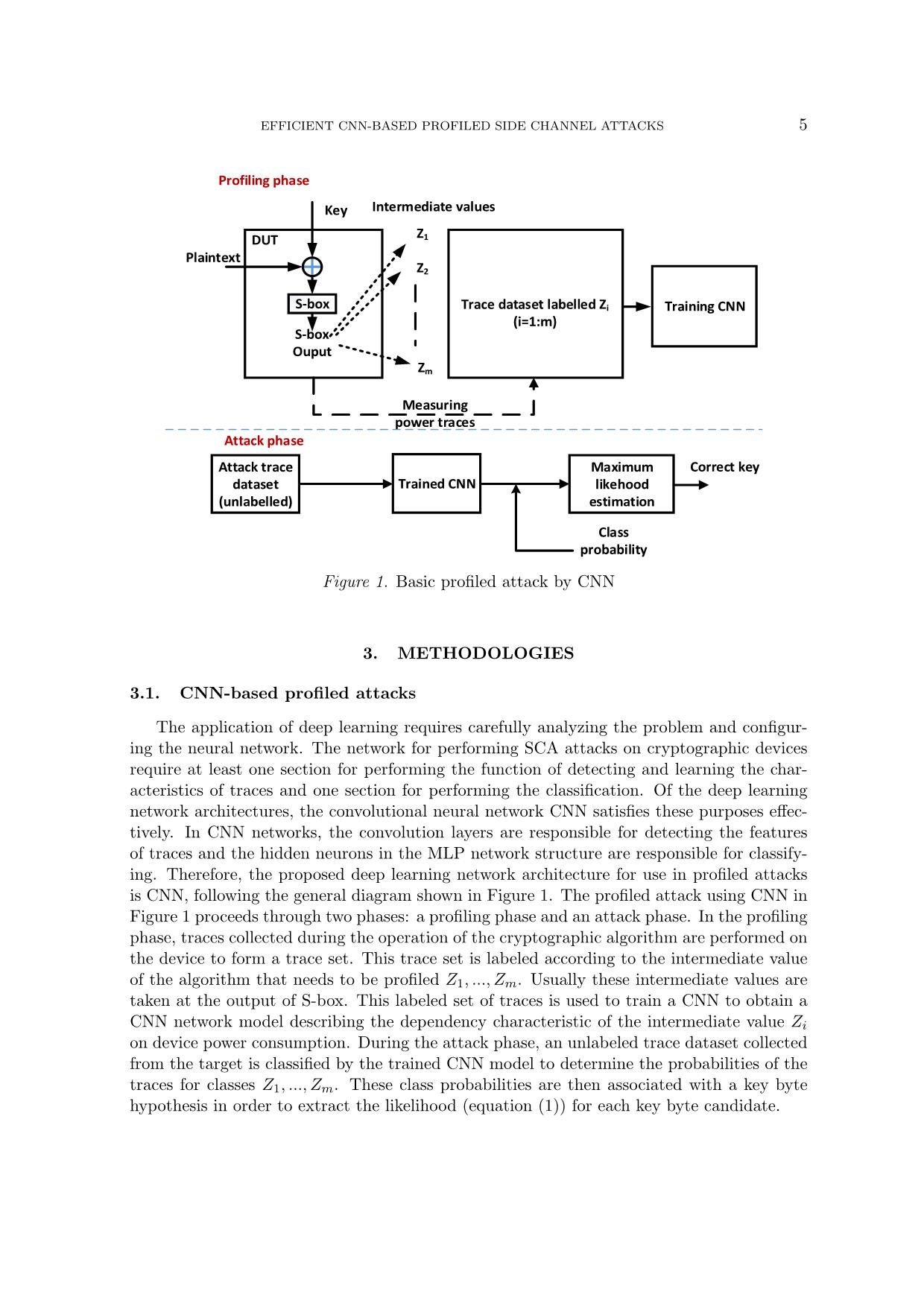
Trang 5

Trang 6
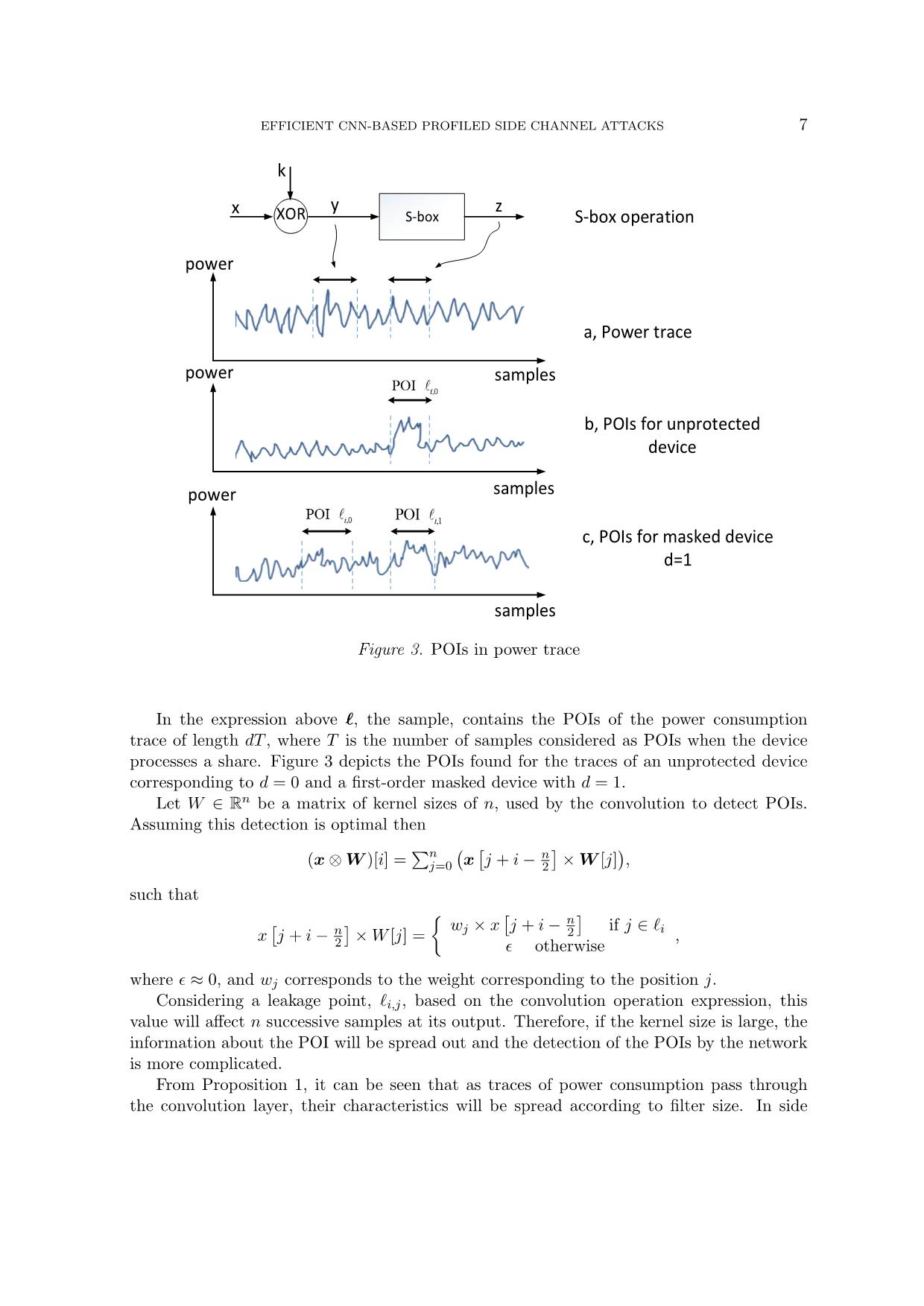
Trang 7

Trang 8
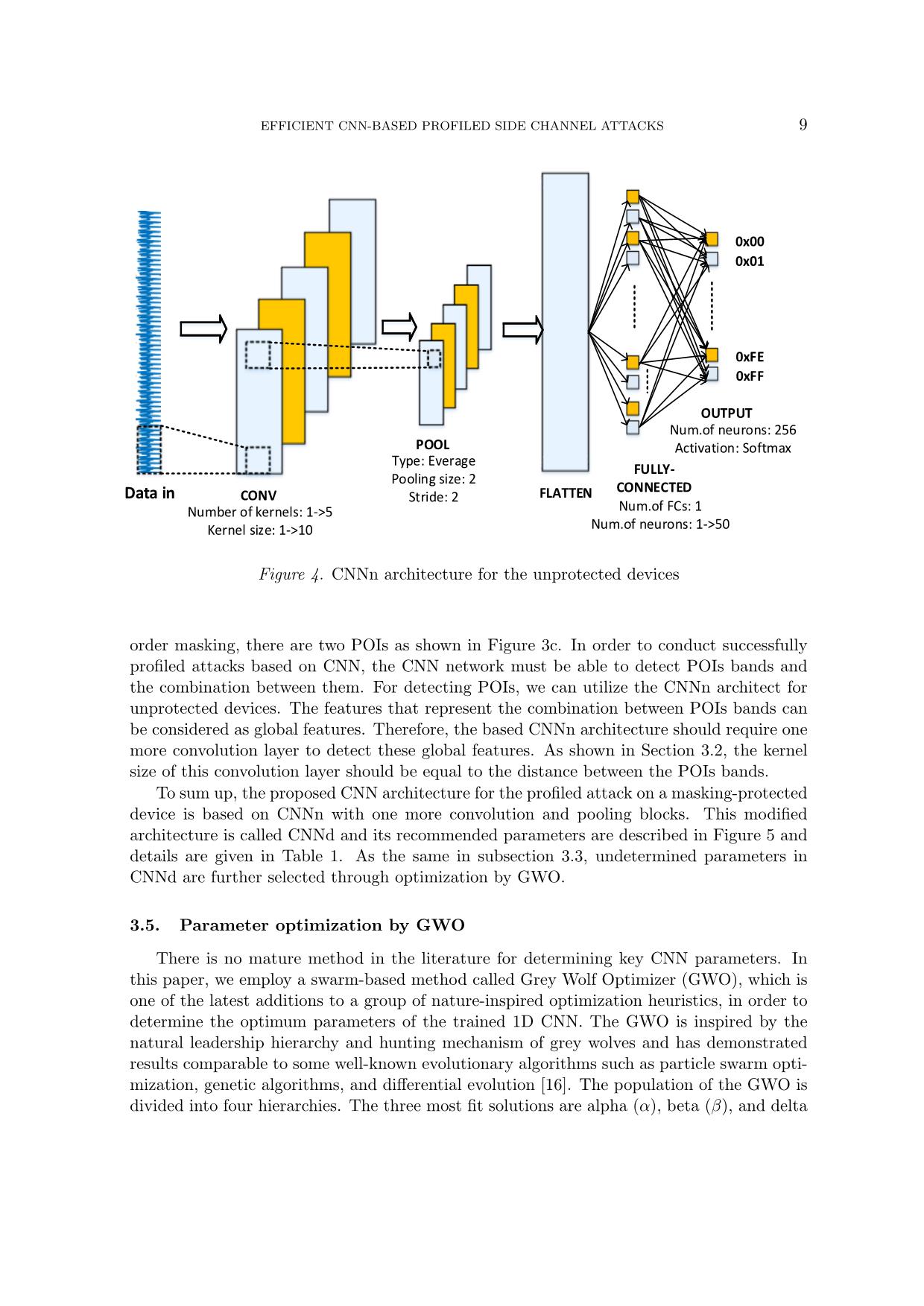
Trang 9
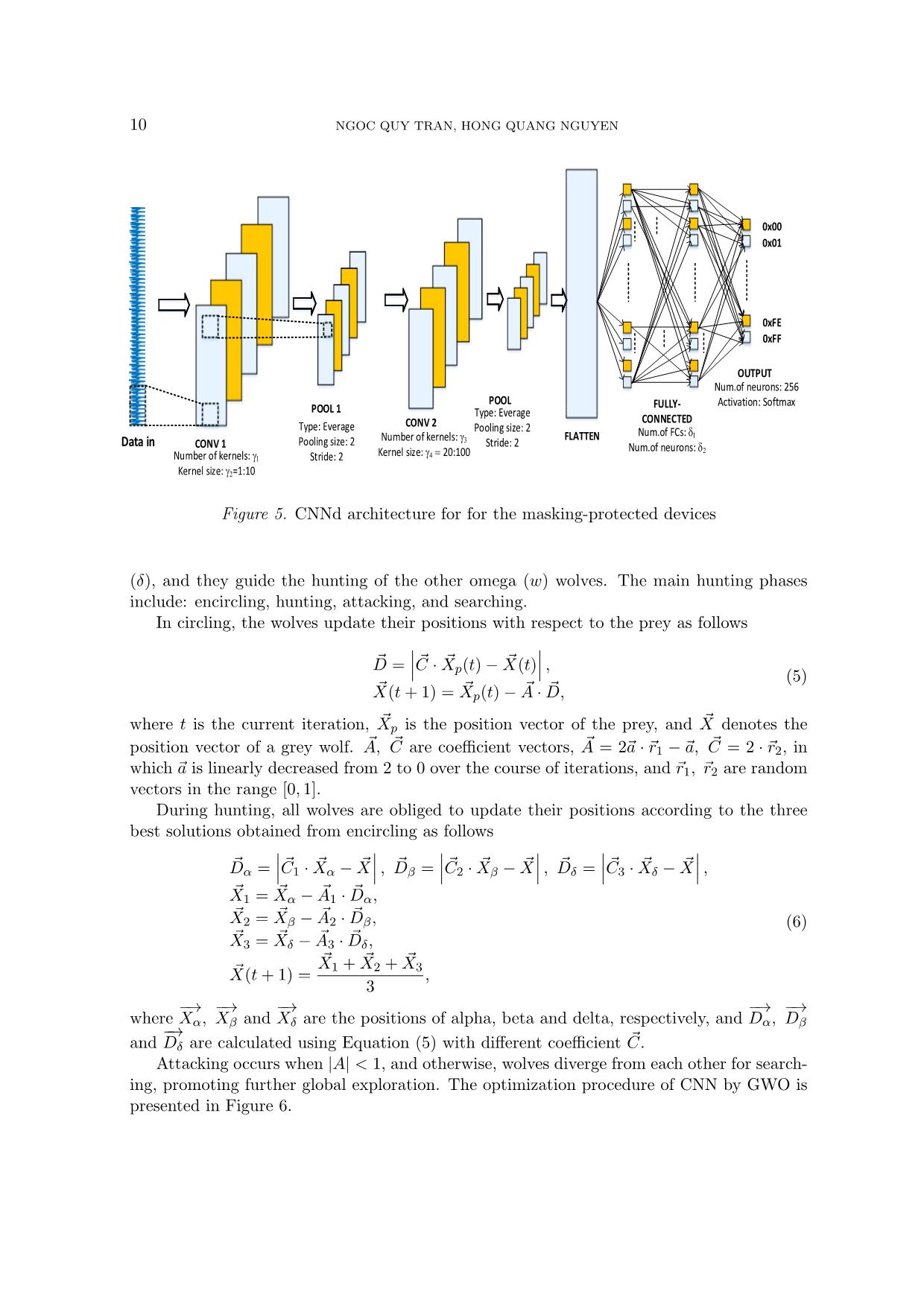
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Efficient CNN - Based profiled side channel attacks

currently considered state-of-the-art results described by Zaid et al. The results of using 4000 traces in the optimization phase to find the parameters for CNNn are shown in Table 4. The CNNn with the parameters given in Table 3 is trained with the 4,000-trace dataset above and then used in the attack phase to find the correct key. The estimated probability of the keys given by Figure 12 shows that the correct key value is 130 with the first byte of the key used in AES-128 having the highest estimated probability. The large distinction between the estimated probability of the correct key and the estimated probability of the other keys reflects this dataset being easy to attack. This result is consistent with the claims made in [22]. Table 4 compares the effectiveness of the proposed method with that of Zaid. The GE values obtained by attacks using both methods are shown in Figure 13. Our CNNn architecture is more effective in terms of the number of traces required for GE to reach 0. Our method requires only 2 traces to reach 0 while Zaid’s method requires 7 traces. This result demonstrates that our CNNn architecture can learn POIs from power traces more precisely than the CNN architecture proposed by Zaid. However, the number of trainable parameters and the training time is more for CNNn than the proposed method of Zaid. Neither of these CNN architectures is too complicated, but they do have good offensive results. Therefore, for unprotected devices, the CNN architecture does not need to be very complicated; only one convolution layer with a small number of kernels and a small kernel size and one FC layer containing relatively few neurons is needed. In this section, we present two experiments of profiled attacks on unprotected devices using our dataset and the DPAContestV4 dataset. Both of them use the same CNN ar- chitecture. Although, according to the theorem “No Free Lunch” [21], there is no optimal architecture for all problems, according to the analysis as well as the experimental results with the two datasets, the CNNn architecture with the parameters given in Table 5 should be used for profiling with unprotected devices. 16 NGOC QUY TRAN, HONG QUANG NGUYEN Correct key:130 1000 Our proposed CNNn 2000 20 Zaid proposed CNN 3000 15 4000 GE 5000 10 6000 5 Probability (Log) 7000 8000 0 0 50 100 150 200 250 0 5 10 15 20 25 30 All hypothetical keys Number of traces Figure 12. Estimation probability of all Figure 13. Guessing entropy results hypothetical keys with Dataset2 for Dataset2 Table 3. CNNn parameters selected by GWO with Dataset2 Parameter Input values of GWO Value after GWO Number of kernels:γ1 1:10 4 Kernel size:γ2 1:10 3 Number of neurons in FC (n) 1:50 10 Table 4. Comparison of performance on Dataset2 Template Attack [22] Zaid et al. method [13] Our proposal Trainable parameters \ 8.782 8.858 Number of traces for GE=0 3 7 2 Training time (s) \ 103 158 Table 5. Optimal parameters of CNNn for unprotected devices Layer Parameter One layer, Activation function SeLU CONV Number of kernels γ1 = 4 Kernel size γ2 = 3 Batch Normalization \ Pooling size = 2; POOL Stride = 2 Flatten \ Number of layers =1 Fully Connected Number of neurons δ1 = 10 Output 256 neurons, softmax activation EFFICIENT CNN-BASED PROFILED SIDE CHANNEL ATTACKS 17 4.5. Results on masking - protected device The experiment in this section uses the DataSet3 dataset, which is divided into 3 parts: 45000 traces for training, 5000 traces for validation, and 10000 traces for the attack. The training and validation data are used by the GWO optimization algorithm to find optimal parameters for the CNNd architecture. The basic CNN architecture used in the experiments in this section is the CNNd proposed in Section 3.4. The parameters optimized for CNNd given in Table 6 are generated by the GWO algo- rithm. Next, CNNd is trained to create a model for data traces. The probabilities of the 256 hypothetical keys estimated in the attack phase are presented in Figure 14, and it is apparent that the maximum probability value corresponds to that of key 224, which is the actual AES-128 key used. Although the probability difference between the right and wrong keys is not substantial, as Figure 15 shows, when the number of attack traces is increased, the probabilities of the wrong keys remain the same, while that of the correct key signifi- cantly increases. Table 7 compares the efficiency of the proposed method to that of Zaid [13] and Prouff [12]. The GE value obtained by attacking using both methods is shown in Figure 16. The CNNd method proposed by us is more effective in terms of the number of traces required to achieve a GE of 0. Our method requires about 183 traces to reach GE = 0 while Zaid’s method requires 195 traces, which represents an approximately 5% reduction. This result demonstrates that our CNNn architecture can learn POIs from the power traces of masked devices more precisely than the CNN architectures proposed by either Zaid or Prouff. However, the number of trainable parameters and the training time of the proposed CNN are larger than those of the method proposed by Zaid yet much smaller than those of the method proposed by Prouff. This can be explained by the architecture of CNNd being more complex than that the architecture used by Zaid yet much simpler than that used by Prouff. Figure 14. Estimation probability of all hypothetical keys with Dataset3 18 NGOC QUY TRAN, HONG QUANG NGUYEN Table 6. CNNd parameters selected by GWO with Dataset3 Parameter Input values of GWO Value after GWO CONV 1 Number of kernels: γ1 1-10 4 Kernel size: γ2 1-10 3 Batch Normalization \ \ POOL 1 Pooling size 2 2 Stride 2 2 CONV 2 Number of kernels: γ3 1-20 8 Kernel size: γ4 20-100 51 Batch Normalization \ \ POOL 2 Pooling size 2 2 Stride 2 2 Flatten \ \ Fully Connected Number of FCs: δ1 1-3 2 Number of neurons/FC: δ2 1-50 10 256 neurons Output Activation function: Softmax Figure 15. Estimation probability of all hypothetical keys against number of traces with Dataset3 EFFICIENT CNN-BASED PROFILED SIDE CHANNEL ATTACKS 19 Figure 16. Guessing entropy results for Dataset3 Table 7. Comparison of performance on DataSet3 Template Attack CNN Profiled attack CNN proposed CNN proposed [12] [12] by Zaid [13] by us Trainable \ 66.652.444 16.960 26.334 parameters Number of traces 450 1.146 195 183 for GE=0 Training time \ 5417 253 790 (s) 5. CONCLUSION In this paper, we have demonstrated that deep learning can be successfully applied to profiled attacks on cryptographic devices. By analyzing the POIs characteristics of power traces and convolution operations, we have proposed two basic CNN architectures, CNNn and CNNd, used for unprotected and masking-protected devices, respectively. The param- eters of the proposed basic CNN architecture are optimized by the GWO algorithm. Our CNNn architecture has minimal complexity, and requires only 2 to 4 traces, to reveal the cor- rect key of unprotected devices. After experimenting successfully on both trace datasets, we claim that CNNn should be the first choice when conducting profiled attacks on unprotected devices. Regarding attacking masking-protected devices, although the architecture of CNNd has one more convolution layer than the CNN architecture of Zaid, it gives better results, specifically a 5% decrease in the number of traces required for GE to equal 0. Therefore, both CNN architectures should be used with the protected device. As a final note, CNN can be used to conduct profiled attacks efficiently assuming its architecture and parameters have been carefully selected. 20 NGOC QUY TRAN, HONG QUANG NGUYEN REFERENCES [1] P. Kocher, J. Jaffe, B. Jun, “Differential Power Analysis,” Advances in Cryptology — CRYPTO’ 99. CRYPTO 1999. Lecture Notes in Computer Science, vol 1666. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-48405-1 25 [2] P .Kocher, “Timing attacks on implementations of DiffieHellman, RSA, DSS, and other sys- tems,” in Proceedings of the 16th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara (USA), 1996. [3] K. Gandolfi, C. Mourtel, G. Oliver, “Electromagnetic analysis: Concrete results,” in Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Paris, 2001. [4] F. Standaert, C. Archambeau, “Using subspace-based template attacks to compare and combine power and electromagnetic information leakages,” in Proceedings of the International Work- shop on Cryptographic Hardware and Embedded Systems - CHES 2008, Washington, D.C (USA), 2008. [5] S. Chari, JR. Rao, P. Rohatgi, ”Template Attacks,” Cryptographic Hardware and Embedded Systems - CHES 2002. CHES 2002. Lecture Notes in Computer Science, vol 2523. Springer, Berlin, Heidelberg. https://doi.org/10.1007/3-540-36400-5 3 [6] E. Brier, C. Clavier,F. Olivier, “Correlation power analysis with a leakage model,” in Interna- tional Workshop on Cryptographic Hardware and Embedded Systems, Springer, 2004, pp. 16–29. https://doi.org/10.1007/978-3-540-28632-5 2 [7] B. Gierlichs, et al, “Mutual information analysis,” Cryptographic Hardware and Embedded Systems – CHES 2008. CHES 2008. Lecture Notes in Computer Science, vol 5154. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-85053-3 27 [8] W. Schindler, K. Lemke, C. Paar, “A stochastic model for differential side channel cryptanalysis,” Cryptographic Hardware and Embedded Systems – CHES 2005. CHES 2005. Lecture Notes in Computer Science, vol 3659. Springer, Berlin, Heidelberg. https://doi.org/10.1007/11545262 3 [9] B. Hettwer, S. Gehrer, T. G¨uneysu,“Applications of machine learning techniques in side-channel attacks: a survey,” J Cryptogr Eng, vol. 10, p. 135–162 , 2020. [10] H. Maghrebi, T. Portigliatti, E. Prouff, “Breaking cryptographic implementations us- ing deep learning techniques,” Security, Privacy, and Applied Cryptography Engineer- ing. SPACE 2016. Lecture Notes in Computer Science, vol 10076. Springer, Cham. https://doi.org/10.1007/978-3-319-49445-6 1 [11] E. Cagli, C. Dumas, E. Prouff, “Convolutional neural networks with data augmentation against jitter-based countermeasures, In Wieland Fischer and Naofumi Homma, edi- tors,Cryptographic Hardware and Embedded Systems – CHES 2017, Cham, Springer In- ternational Publishing, 2017, pp. 45–68. [12] E. Prouff, R. Strullu, R. Benadjila, E. Cagli, C. Dumas, “Study of deep learning techniques for side-channel analysis and introduction to ascad database,” Cryptology ePrint Archive, Report 2018/053, 2018, https://eprint.iacr.org/2018/053, 2018 [13] G. Zaid, L. Bossuet, A. Habrard, A. Venelli, “Methodology for efficient cnn architectures in profiling attacks,” IACR Transactions on Cryptographic Hardware and Embedded Systems, IACR, 2020, 2020 (1), pp.1-36. Doi: https://doi.org/10.13154/tches.v2020.i1.1-36 EFFICIENT CNN-BASED PROFILED SIDE CHANNEL ATTACKS 21 [14] J. Heaton, I. Goodfellow, Y. Bengio, A. Courville, Deep Learning, MIT Press, 2016. [15] S. Ioffe, C. Szegedy, “Batch normalization: Accelerating deep network training by reducing in- ternal covariate shift,” in Proceedings of the 32nd International Conference on International Conference on Machine Learning, 2015. [16] S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [17] F. Chollet et al, “Keras,” https://keras.io, 2015. [18] L.N. Smith, N. Topin, “Super-convergence: Very fast training of residual networks using large learning rates,” in ICLR 2018 Conference, CoRR, 2018. [19] G. Klambauer, T. Unterthiner, A. Mayr, S. Hochreiter, “Self-normalizing neural networks,” arXiv:1706.02515. [20] K. He, X. Zhang, S. Ren, J. Sun, “Delving deep into rectifiers: Surpassing human-level perfor- mance on imagenet classification,” in Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), ICCV ’15, Washington, DC, USA, 2015, pages 1026–1034. [21] D.H. Wolpert, W.G. Macready, “No free lunch theorems for optimization,” IEEE Trans. Evo- lut. Comput, vol. 1, no. 1, pp. 67–82, 1997. [22] J. Kim, S. Picek, A. Heuser, S. Bhasin, A. Hanjalic, “Make some noise. Unleashing the power of convolutional neural networks for profiled side-channel analysis”, IACR Transac- tions on Cryptographic Hardware and Embedded Systems, vol. 2019, no. 3, pp. 148–179. https://doi.org/10.13154/tches.v2019.i3.148-179 [23] S. Mangard, E. Oswald, T. Popp, Power Analysis Attacks Revealing the Secrets of Smart Cards, New York: USA: Springer, 2010. [24] A. Heuser and M. Zohner, “Intelligent machine homicide breaking cryptographic devices using support vector,” in COSADE 2012, Heidelberg, 2012. [25] G. Hospodar, B. Gierlichs, E. De Mulder, I. Verbauwhede, J. Vandewalle, “Machine learning in side-channel analysis: A first study,” J Cryptogr Eng, vol. 1, article number 293, 2011. https://doi.org/10.1007/s13389-011-0023-x [26] G. Hospodar, E. De Mulder, B. Gierlichs, J. Vandewalle, and I. Verbauwhede, “Least squares support vector machines for side-channel analysis,” in COSADE 2011, Darmstadt, 2011. [27] L. Lerman, S. F. Medeiros, G. Bontempi, and O. Markowitch, “A machine learn- ing approach against a masked AES,” J Cryptogr Eng, vol. 5, pp. 123–139, 2015. https://doi.org/10.1007/s13389-014-0089-3 [28] S. Picek, A. Heuser, A. Jovic, S.A. Ludwig, S.Guilley, D. Jakobovic, N. Mentens, “Side- channel analysis and machine learning: A practical perspective,” 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, 2017, pp. 4095-4102. Doi: 10.1109/IJCNN.2017.7966373. [29] S. Picek, A. Heuser, A. Jovic, L. Batina, and A. Legay, “The secrets of profiling for side-channel analysis: feature selection matters,” IACR Cryptology ePrint Archive, 2017. 22 NGOC QUY TRAN, HONG QUANG NGUYEN [30] Y. Zheng, Y. Zhou, Z. Yu, C. Hu, H. Zhang, “How to compare selections of points of inter- est for side-channel distinguishers in practice?,” in Information and Communications Secu- rity. ICICS 2014. Lecture Notes in Computer Science, vol 8958. Springer, Cham, 2014. https://doi.org/10.1007/978-3-319-21966-0 15 [31] Y. Kong, E. Saeedi, “The investigation of neural networks performance in side channel attacks,” Artif Intell Rev, vol. 52, pp. 607–623, 2019. https://doi.org/10.1007/s10462-018-9640-4 [32] F. Standaert, T. Malkin, M. Yung, “A unified framework for the analysis of side-channel key recovery attacks,” Advances in Cryptology - EUROCRYPT 2009. EUROCRYPT 2009. Lecture Notes in Computer Science, vol 5479. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-01001-9 26 Received 25 August 2020 Accepted 14 January 2021
File đính kèm:
 efficient_cnn_based_profiled_side_channel_attacks.pdf
efficient_cnn_based_profiled_side_channel_attacks.pdf

