Design and simulation of scanning probe micro - cantilever for the scanning probe lithography

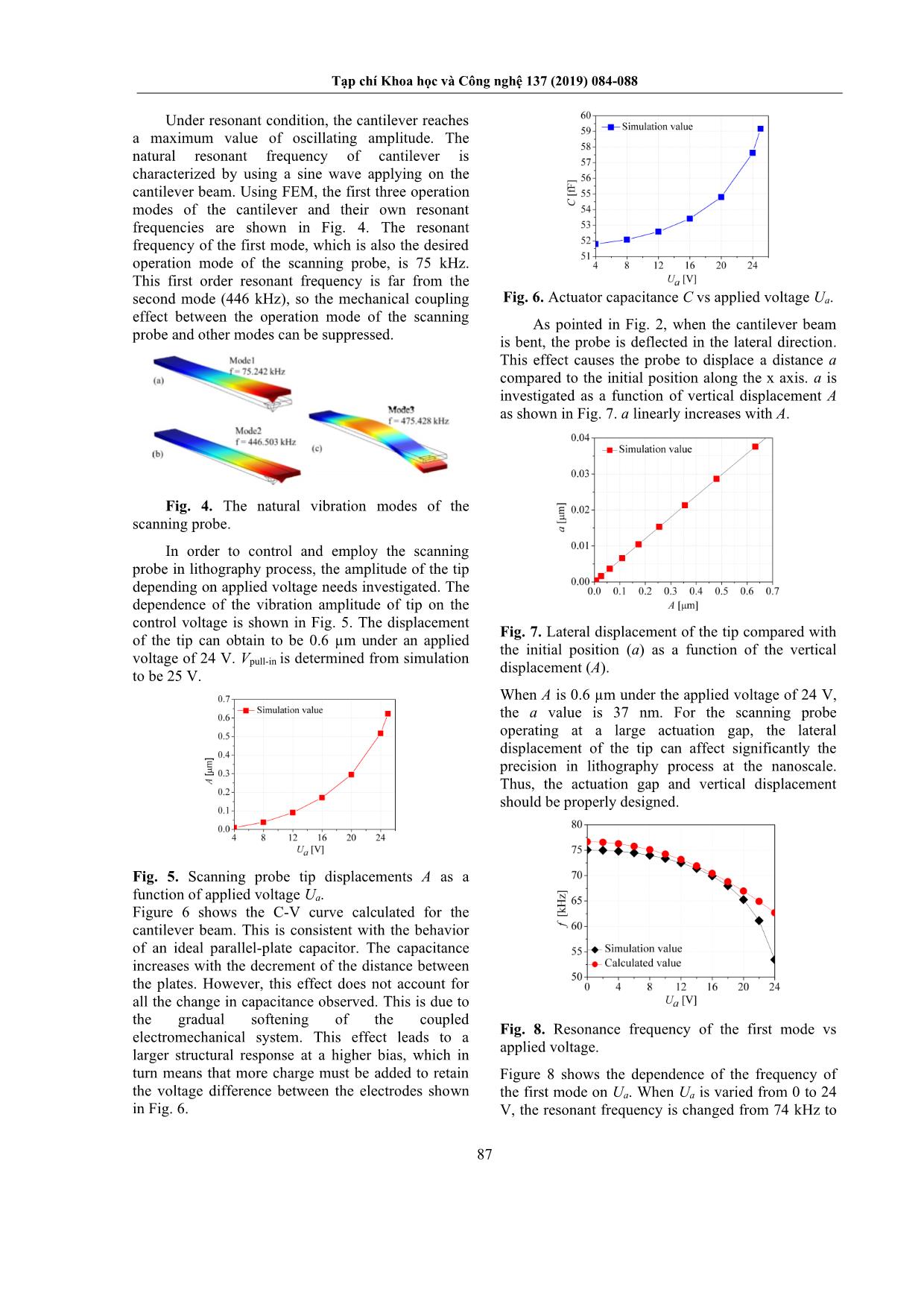
ation 
voltage are simulated by finite element method 
(FEM) and verified by analysis expressions. The pull-
Tạp chí Khoa học và Công nghệ 137 (2019) 084-088 
85 
in effect affecting the operation of the scanning probe 
is also studied. The deviation of the probe during the 
operation process is investigated in detail. This 
research is to improve the precision control and 
resolution of the lithography technology using 
scanning probe. 
2. Design of Scanning Probe Micro-cantilever 
The structure of scanning probe micro-
cantilever is designed with an actuation beam. The 
dimensions of the actuation beam, length (L), width 
(w), and height (h) are 300 μm, 30 μm, and 5 μm, 
respectively. One end of the beam is fixed, the other 
is free. A sharp probe tip is integrated at the free end 
of the actuation beam. The tip has the atom-sized 
pyramid shape, which is 14 μm bottom edge and 10 
μm height. 
Fig. 1. Structure of the cantilever beam and probe tip. 
Fig. 2. Boundary conditions of the scanning probe 
micro-cantilever. 
The entire microcantilever, which is made of 
single crystalline silicon, is operated in the air 
environment. In order to actuate the tip, a fixed 
conductive electrode is placed parallel to the back 
side of the cantilever beam to form a capacitive 
actuation. The gap of the capacitive actuation is 2 
µm. The tip is driven by placing a control voltage on 
the fixed electrode. The effect of electrostatic 
attractive force makes the cantilever beam carrying 
the scanning tip to vibrate. The structure of the 
scanning probe micro-cantilever and its structure 
parameters are shown in Fig. 1. 
In order to simulate the operation characteristics 
of the scanning probe, FEM is used. FEM is a 
numerical method to solve problems described by the 
partial differential equations with specific boundary 
conditions. The basis of this method is to discretize 
the continuous domain of the complex problem. The 
constant domain is divided into sub domains (called 
elements). These domains are linked together at the 
nodes. On this sub-domain, equivalent vibration 
problems are roughly based on approximate functions 
on each element, satisfying the conditions on the 
wings with balance and continuity between elements. 
Figure 2 illustrates an operation state and 
boundary conditions of the scanning probe micro-
cantilever used in simulation. Boundary conditions of 
the system are as follows: (1) one end of the 
cantilever is fixed at x = 0 and (2) the other is free, as 
shown in Fig. 2. The x axis is along cantilever length 
and A(x) is the vertical deflection of cantilever at a 
position x. The free vibration equation of the 
cantilever is given as [12]: 
4
2
4
( ) 0
w
EI A x
x


− =

, (1) 
where E is the elastic modulus, I is the second 
moment of area, ω is the natural angular frequency 
and  is the mass per unit length. The boundary 
conditions for the cantilever beam are: 
( ) 0A x = and ' ( ) 0A x = at 0x = ; 
'' ( ) 0A x = and ''' ( ) 0A x = at x L= . 
If we apply these conditions, non-trivial solutions of 
Eq. (1) are found to exist only if 
( ) ( )osh os 1 0c L c Ln n  + = , (2) 
where 
1/4
2
n
EI


= 
. (3) 
The nonlinear equation, Eq. (2), can be solved 
numerically for
nL and the corresponding natural 
frequencies of vibration are [12]: 
2
2 2
n n
n
EI
f = =
 
 
. (4) 
Table 1. The values of nL and nf for first three 
modes 
Mode 
nL nf [ kHz] 
1 1.875 76.651 
2 4.694 480.604 
3 7.855 1345.267 
The values of nL and nf for the first three modes 
are shown in Table 1. 
Tạp chí Khoa học và Công nghệ 137 (2019) 084-088 
86 
Fig. 3. Mode shapes for the first three modes of 
vibrating cantilever beam. 
General solution of Eq. (1) is given by: 
(cos osh )(sin sinh )
ˆ cosh os1 sin sinh
L c L x x
n n n nw A x c xn n n L L
n n
   
 
 
 + −
 = − +
 +
. (5) 
The mode shapes of the cantilever beam are 
illustrated in Fig. 3, each line shows the vibration of 
the cantilever with a different natural frequency. 
When control voltage is set on the fixed 
electrode of the cantilever actuation capacitor, 
electrostatic attraction makes the cantilever beam to 
bend. If the voltage increases to a certain value, the 
system nonlinearity appears that leads to the pull-in 
phenomena. This voltage is called to be pull-in 
voltage, Vpi [13]. Vpi is evaluated by 
1
4 2
0 2 3
4
25.41
1
PI
c B
V
g
L c c
w
= =
+ 

V. (6) 
Here c1 = 0.07, c2 = 1.00, c3 = 0.42 and B is 
 3 3 261.7 10B Eh g −= = . (7) 
E is evaluated by 
( )
( )
( )
0.056
0.98 /
1.37
2
1.37
/
1
0.5 /
L h
w LE
E w L
−
 = −
 + 
. (8) 
E is Young’s modulus and  is Poisson’s ratio. 
The capacitance of the cantilever actuator is 
calculated by expression: 
39.84o
S
C
g
= =

 fF, (9) 
where S is the effective back-side area (effective 
capacitor electrode area) of cantilever and 0 is the 
dielectric constant of air. 
When voltage applying on the micro-cantilever 
is varied, g will change. This means that the 
capacitance value depends on applied voltage on the 
cantilever beam. The gap is designed to be smaller 
than one-third of the width of the cantilever. When 
the actuator operates under atmospheric condition, 
squeeze air film damping dominates [14]. The cut-off 
frequency of the squeeze air film damping is [14]: 
2 2
2
2
12
a
c
g p
f
w
= =

MHz, (10) 
where, 
ap is the atmospheric pressure.  is the 
coefficient of viscosity of the air. 
The operation frequency of the actuator is 75 
kHz, smaller than the cut-off frequency. Therefore, 
the squeeze film damping relating to viscous flow of 
air is dominant. The quality factor of the micro-
cantilever ( )Q is given by [15]: 
2 3
2.66
w E h g
Q
L w

= = 
. (11) 
Thus, Q is proportional to h and g and inversely 
proportional to L and w. It is an effective way to 
increase Q by reducing L and w and/or increasing 
either g or h. However, if L and w are decreased, the 
effective capacitor electrode area S is consequently 
decreased. This leads to the reduction in the actuation 
capacitance. Moreover, the dependence of the 
response characteristic of the scanning probe on time 
shows that the Q value and resonant frequency affect 
the response and recovery time [16]. 
To achieve high performance, the actuator is 
required to operate in the resonance mode. It is 
excited by electrostatic force and there are two 
applied voltage components on the actuator, direct 
current (DC) voltage and alternating current (AC) 
voltage. When the DC voltage is increased, the 
resonance frequency of the actuator is decreased. This 
effect is called the spring softening effect. The 
actuator can be assumed to be a parallel-plate 
capacitor. The natural frequency of cantilever is given 
by [16]: 
2
3
oAVkf
m mg

= − , (12) 
3
8EI
k
L
= , (13) 
where k is the stiffness coefficient, I is the moment of 
inertia of the cross section, and m is effective mass. 
3. Results and discussion 
Tạp chí Khoa học và Công nghệ 137 (2019) 084-088 
87 
Under resonant condition, the cantilever reaches 
a maximum value of oscillating amplitude. The 
natural resonant frequency of cantilever is 
characterized by using a sine wave applying on the 
cantilever beam. Using FEM, the first three operation 
modes of the cantilever and their own resonant 
frequencies are shown in Fig. 4. The resonant 
frequency of the first mode, which is also the desired 
operation mode of the scanning probe, is 75 kHz. 
This first order resonant frequency is far from the 
second mode (446 kHz), so the mechanical coupling 
effect between the operation mode of the scanning 
probe and other modes can be suppressed. 
Fig. 4. The natural vibration modes of the 
scanning probe. 
In order to control and employ the scanning 
probe in lithography process, the amplitude of the tip 
depending on applied voltage needs investigated. The 
dependence of the vibration amplitude of tip on the 
control voltage is shown in Fig. 5. The displacement 
of the tip can obtain to be 0.6 µm under an applied 
voltage of 24 V. Vpull-in is determined from simulation 
to be 25 V. 
Fig. 5. Scanning probe tip displacements A as a 
function of applied voltage Ua. 
Figure 6 shows the C-V curve calculated for the 
cantilever beam. This is consistent with the behavior 
of an ideal parallel-plate capacitor. The capacitance 
increases with the decrement of the distance between 
the plates. However, this effect does not account for 
all the change in capacitance observed. This is due to 
the gradual softening of the coupled 
electromechanical system. This effect leads to a 
larger structural response at a higher bias, which in 
turn means that more charge must be added to retain 
the voltage difference between the electrodes shown 
in Fig. 6. 
Fig. 6. Actuator capacitance C vs applied voltage Ua. 
As pointed in Fig. 2, when the cantilever beam 
is bent, the probe is deflected in the lateral direction. 
This effect causes the probe to displace a distance a 
compared to the initial position along the x axis. a is 
investigated as a function of vertical displacement A 
as shown in Fig. 7. a linearly increases with A. 
Fig. 7. Lateral displacement of the tip compared with 
the initial position (a) as a function of the vertical 
displacement (A). 
When A is 0.6 µm under the applied voltage of 24 V, 
the a value is 37 nm. For the scanning probe 
operating at a large actuation gap, the lateral 
displacement of the tip can affect significantly the 
precision in lithography process at the nanoscale. 
Thus, the actuation gap and vertical displacement 
should be properly designed. 
Fig. 8. Resonance frequency of the first mode vs 
applied voltage. 
Figure 8 shows the dependence of the frequency of 
the first mode on Ua. When Ua is varied from 0 to 24 
V, the resonant frequency is changed from 74 kHz to 
Tạp chí Khoa học và Công nghệ 137 (2019) 084-088 
88 
54 kHz. This effect needs to be taken into considering 
the actuation of the scanning probe. When the 
actuator operates with a high quality factor (Q), the 
resonant frequency shift affects significantly the 
actuation amplitude of the scanning probe. In this 
case, the resonance peak of actuator is sharp and 
highly sensitive to frequency shift. 
Fig. 9. Schematic drawing of the improved scanning 
probe (a) and the first operation mode of the 
improved scanning probe (b). 
In the above analysis, the scanning probes using 
cantilever-type actuation structure in which the probe 
is integrated at the free end of a fixed-free beam. The 
operation mode of scanning probe is unsymmetrical, 
which limits the controllable precision of 
lithographed structures. So, we propose an 
electrostatic actuator for improving the limitation in 
lithography process causing by the unsymmetrical 
operation mode of cantilever-type actuator as shown 
in Fig. 9 (a). Fig. 9 (b) shows the first operation mode 
of the improved scanning probe. In general, the 
displacement of the tip quadratically varies with 
applied voltage. To obtain a displacement of 0.6 µm, 
the scanning probe with the proposed fixed-fixed 
beam type actuation needs an applied voltage of 40 V 
instead of 24 V as in the case of the conventional 
cantilever-type scanning probe. This applied voltage 
is noticeably low compared to the previously 
designed value. This is also preferred for the 
application control. 
4. Conclusion 
This paper presents the design and simulation of 
operational characteristics of a scanning probe micro-
cantilever. The operational characteristics of the 
scanning probe micro-cantilever are simulated by 
finite element method. The operation frequency of 
micro-cantilever is 75 kHz. The tip of probe can 
obtain a displacement of 0.6 µm at an actuation 
voltage of 24 V. The lateral displacement of the tip is 
also investigated as a function of the vertical 
displacement, which significantly affects the 
precision of lithography process at the nanoscale. An 
electrostatic actuator for improving the limitation in 
lithography process causing by the unsymmetrical 
operation mode of cantilever-type actuator is also 
proposed. 
References 
[1]. D. S. Ginger at.al., The evolution of dip-pen 
nanolithography, Angew.Chem. Int. Ed. 43 (2004) 
30-45. 
[2]. P. J. Thomas, G. U. Kulkarni and C. N. R. Rao, Dip-
pen lithography using aqueous metal nanocrystal 
dispersions, J. Mater. Chem., 1 4 (2004) 625 – 628. 
[3]. X. Liu, Y. Li and Z.Zheng, Programming 
nanostructures of polymer brushes by dip-pen 
nanodisplacement lithography (DNL), Nanoscale, 2 
(2010) 2614–2618. 
[4]. E. J. Irvine, A. H. Santana, K.Faulds and D. Graham, 
Fabricating protein immunoassay arrays on 
nitrocellulose using Dip-pen lithography techniques, 
Analyst, 136 (2011) 2925. 
[5]. J. Y. Son, Y. H. Shin, S. Ryu, H. Kim, and H. M. 
Jang, Dip-Pen Lithography of Ferroelectric PbTiO3 
Nanodots, J. Am. Chem. Soc. 131 (2009) 14676–
14678. 
[6]. L. V. Tam, D. V. Hieu, N. D. Vy, V. N. Hung, C. M. 
Hoang, Design and simulation analysis of an 
electrostatic actuator for improving the performance 
of scanning probe nanolithography, Vietnam Journal 
of Science and Technology 55 (4) (2017) 484-493. 
[7]. D. J. Resnick, S.V. Sreenivasan, and C.G. Willson, 
Step & flash imprint lithography, Mater. Today, 8(2) 
(2005) 34–42. 
[8]. Zheng Cui, Nanofabrication, Principles, Capabilities 
and Limits, 151, Springer Science+Business Media, 
(2008). 
[9]. D.Bullen, C. Liu, Electrostatically actuated dip pen 
nanolithography probe arrays, Sensors and Actuators 
A 125 (2006) 504–511. 
[10]. A.Gaitas, P. French, Piezoresistive Probe Array for 
High Throughput Applications, Procedia Engineering 
25 (2011) 1445 – 1448. 
[11]. X. Wang, D. A. Bullen, J.Zou, and C. Liu, Thermally 
actuated probe array for parallel dip-pen 
nanolithography, J. Vac. Sci. Technol. B 22(6) (2004) 
2563-2567. 
[12]. O. Brand, I. Dufour, S. Heinrich, F. Josse, Resonant 
MEMS: Fundamentals, Implementation, and 
Application (Advanced Micro and Nanosystems), 16-
18, Wiley-VCH, the 1st edition (2015) 
[13]. R.K. Gupta, Electrostatic Pull-In Structure Design for 
In-Situ Mechanical Property Measurements of 
Microelectromechanical Systems (MEMS), Ph.D. 
thesis, MIT, 1997. 
[14]. M. Bao, H. Yang, Squeeze film air damping in 
MEMS, Sensors and Actuators A 136 (2007) 3–27. 
[15]. M. I. Younis, MEMS Linear and Nonlinear Statics 
and Dynamics, 225, Springer Science+Business 
Media, (2011). 
[16]. S. Abe, M. H. Chu, T. Sasaki, and K. Hane, Time 
Response of a Microelectromechanical Silicon 
Photonic Waveguide Coupler Switch, IEEE Photon. 
Technol. Lett, 26(15), (2014),1553-1556.