Đáp ứng khí động học của một kết cấu cột theo phương vuông góc với hướng gió

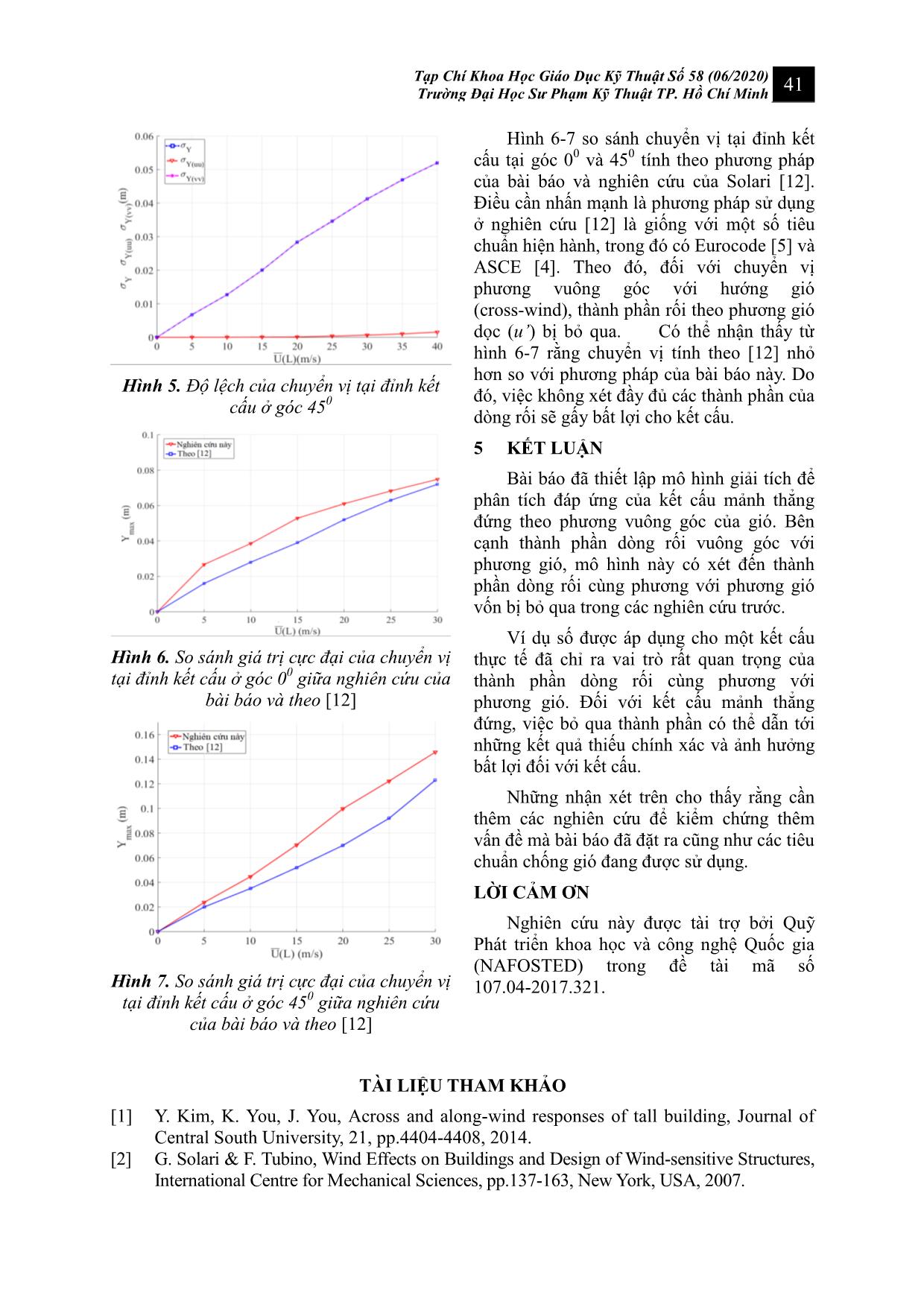
ó cũng thường 
được phân tích thành 3 thành phần cùng 
phương tương ứng. Với kết cấu thẳng đứng 
thì thành phần dòng rối theo phương thẳng 
đứng không gây ra chuyển vị. Do đó, hai 
thành phần chuyển vị được quan tâm là 
chuyển vị theo phương gió (along-wind) và 
phương vuông góc với phương gió 
(cross-wind). 
Hơn 60 năm qua, đáp ứng động của kết 
cấu mảnh chịu tác động của gió là một trong 
những chủ đề quan trọng trong lĩnh vực kỹ 
thuật gió. Nhiều nghiên cứu đã được đề xuất 
bằng các phương pháp khác nhau như: 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 58 (06/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
37 
phương pháp giải tích, phương pháp số, thí 
nghiệm bằng hầm gió cũng như các công cụ 
đo đạc thực tế [1]. Các nghiên cứu đầu tiên 
được thực hiện từ thập niên 1960 với sự đóng 
góp tiên phong của Davenport [2, 3]. Ông đã 
tính các dạng dao động cơ bản và chuyển vị 
trung bình theo phương tác động và vuông 
góc với phương gió. Nhiều mô hình sau này 
đã được đề xuất để cải tiến những nghiên cứu 
của Davenport. Tuy nhiên, các nghiên cứu 
này vẫn chưa hoàn thiện. Các mô hình này 
được tổng hợp ở tài liệu [2]. 
Các nghiên cứu trước và các tiêu chuẩn 
thiết kế hiện hành sử dụng nhiều mô hình 
khác nhau để tính toán các đáp ứng của kết 
cấu do gió theo phương vuông góc với 
phương gió [4, 5]. Trong đó, thành phần 
dòng rối cùng phương gió thường bị bỏ qua 
mà chỉ xét đến thành phần dòng rối vuông 
góc với phương gió [6, 7]. Điều này giúp cho 
các kỹ sư thiết kế có những công thức đơn 
giản hơn trong việc tính toán ứng xử của kết 
cấu do gió. Tuy nhiên, nó có thể dẫn tới kết 
quả thiếu chính xác vì các thành phần của 
dòng rối đều có thể tác động đến chuyển vị 
của kết cấu. 
Xuất phát từ những nhận xét trên, bài 
báo này nhằm xây dựng bài toán phân tích 
đáp ứng chuyển vị của kết cấu theo phương 
vuông góc với phương gió. Thành phần dòng 
rối cùng phương với phương gió, vốn thường 
bị bỏ qua, đều được xem xét trong nghiên 
cứu này. Lý thuyết phổ và dao động ngẫu 
nhiên sẽ được áp dụng trong việc thiết lập lý 
thuyết tính toán. Để minh họa và kiểm chứng 
lý thuyết, một áp dụng cho kết cấu thực tế và 
so sánh kết quả tính toán với các cách tính 
toán hiện có sẽ được tiến hành. Từ đó, vai trò 
của các thành phần khác nhau của dòng rối 
đến chuyển vị kết cấu sẽ được làm rõ. 
2. CƠ SỞ LÝ THUYẾT 
Xét một kết cấu mảnh thẳng đứng có 
chiều cao L, bề rộng đón gió B, có tiết diện 
bất kì như Hình 1 trong hệ trục tọa độ 
Decartes Oxyz. Trục z trùng với trục kết cấu. 
Kết cấu chịu tác động của gió có vận tốc 
trung bình U z cùng hướng với trục x. 
Đối với kết cấu thẳng đứng, vận tốc gió tức 
thời ,U z t có thể được biểu diễn bởi [2]: 
 , , ,U U u' v'z t z z t z t (1) 
Trong đó u là thành phần rối theo phương 
tác động (cùng phương với trục x – 
along-wind); v là thành phần rối theo 
phương vuông góc với gió (cùng phương với 
trục y cross-wind), t là thời gian. 
Hình 1. Tác động khí động lực học theo 
phương vuông góc lên một tiết diện bất kỳ tại 
độ cao z; α: góc tác động [2],[6] 
Phương trình chuyển động của hệ theo 
phương vuông góc (phương y) theo [8]: 
, , ,
,y
m z Y z t c z Y z t k z Y z t
F z t
 (2) 
 , ,y y yF z t F z F z t (3) 
Trong đó yF (N/m) là lực gió trung bình 
theo phương y, phân bố trên một đơn vị chiều 
dài; yF (N/m) là lực gió theo phương y, 
phân bố trên một đơn vị chiều dài, gây ra bởi 
dòng rối; Y (m) là chuyển vị theo phương y; 
Y (m/s) là vận tốc theo phương y; Y (m/s2) 
là gia tốc theo phương y; k (N/m2) là độ 
cứng; c (Kg/ms) là hệ số cản; m (Kg/m) là 
khối lượng phân bố trên một đơn vị chiều dài 
của hệ. 
Áp dụng giả thiết về tính dừng trong dao 
động (quasi-steady theory) và giả thiết 
'U u , 'U v , với U U , 'u' u
'v' v là các thành phần vận tốc (m/s), 
lực tác động của gió như sau [2]: 
 2
1
2
y LF z BU z C (4) 
38 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 58 (06/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
, '
1
' '
2
y L
D L
F z t U z BC u t
U z B C C v t
 (5) 
Trong đó CD và CL lần lượt là hệ số lực 
đẩy (drag) và nâng (lift); C '
L
 là đạo hàm 
của C
L
 theo góc tác động; ρ (Kg/m3) là 
khối lượng riêng của không khí. 
Đối với kết cấu vẫn còn làm việc trong 
giai đoạn đàn hồi tuyến tính thì chuyển vị có 
thể được phân tích thành: 
 , ' ,Y z t Y z Y z t (6) 
Trong đó Y (m) và 'Y (m) lần lượt là đáp 
ứng chuyển vị gây ra bởi 
yF và yF . 
Giả thiết rằng bề mặt nhám địa hình 
đồng nhất tại vị trí đang xét; phản ứng của 
kết cấu vẫn còn trong giai đoạn đàn hồi tuyến 
tính; dạng dao động riêng đầu tiên là ảnh 
hưởng đáng kể nhất; các dạng dao động riêng 
còn lại (bậc hai trở lên) xem như tác động 
không đáng kể [2, 8, 9]. Thành phần trung 
bình của chuyển vị Y được cho bởi [8]: 
1
0
2
1 12
L
yF z z dz
Y z
m f

 (7) 
Trong đó 1 z là dạng dao động riêng thứ 
1 của kết cấu; 1f (Hz) là tần số riêng của kết 
cấu ở dạng dao động riêng thứ 1; 1m (Kg) 
là khối lượng suy rộng (generalised mass) 
tương ứng dạng dao động thứ 1: 
 21 1
0
L
m m z z dz (8) 
Đáp ứng chuyển vị 'Y là hàm ngẫu 
nhiên theo thời gian. Nếu xem gió là một quá 
trình ngẫu nhiên có tính dừng, đồng nhất và 
ergodic thì các giá trị này có thể được xử lý 
theo lý thuyết dao động ngẫu nhiên được rút 
ra từ các giá trị phương sai [1, 8]: 
 2
0
Y Yz S f df
 (9) 
Trong đó YS (m
2
) là phổ đáp ứng của yF 
trong miền tần số; 2Y (m
2
) là phương sai 
của chuyển vị theo phương vuông góc 
(phương y). 
Áp dụng lý thuyết phân tích theo phổ, 
YS 
có thể được tính toán như sau [10]: 
2
1 2
1 2
0 0 1 1 1 2 1 2
2
1 2
1 2
0 0 1 1 1 2 1 2
2
1 2
1 2
0 0
1 1 1 2 1 2
, ,
'
, z ,
1
'
2
S , ,
L L
L
Y
uu
L L
D L L
uv
L L
D L
vv
BC U z U z
S f dz dz
z z S z z f
B C C C U z U z
dz dz
z z S z f
B C C U z U z
dz dz
z z z z f
 
 
 
 
 
 
 
  
 
 (10) 
Trong đó Sab là phổ của thành phần rối a,b. 
Đối với kết cấu thẳng đứng, thành phần 
dòng rối u’, v’ hầu như không tương quan 
(uncorrelated) với nhau [2]. Do đó, công thức 
(9) được viết lại thành: 
 2 2 2( ) ( )Y Y uu Y vvz z z   (11) 
Trong đó 2( )Y uu (m
2
) là phương sai của 
chuyển vị theo phương vuông góc do thành 
phần khí rối phương tác động gây ra; 2( )Y vv 
(m
2
) là phương sai của chuyển vị theo 
phương vuông góc do thành phần khí rối 
phương vuông góc gây ra. 
2
1 2
2
( ) 1 1 1 2 1 2
0 0 0
1 2, ,
L
L L
Y uu
uu
BC U z U z
z z z dz dz df
S z z f
  
 (12) 
2
2
1 2
( ) 1 2
0 0 0
1 1 1 2
1 2
1
'
2
S , ,
D L
L L
Y vv
vv
B C C
U z U zz dz dz df
z z
z z f

 
 (13) 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 58 (06/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
39 
Giá trị cực đại của chuyển vị tại độ cao z 
sẽ bằng tổng chuyển vị trung bình và chuyển 
vị lớn nhất ở độ cao đó [8]: 
 max Y YY z Y z g z (14) 
Trong đó g
y
 là hệ số đỉnh (Peak factor) 
theo phương vuông góc y, xác định bởi lý 
thuyết phân bố cực trị tiệm cận. 
3. HÀM PHỔ CỦA CÁC THÀNH 
PHẦN RỐI 
3.1 Hàm phổ S
uu
(z
1
,z
2
,f) 
Phổ gió uuS của thành phần rối u’ được 
cho bởi [2, 9, 11]: 
1 2 1 2
1 2
, , , ,
coh , ;
uu u u
uu
S z z f S z f S z f
z z f
 

 (15) 
Trong đó 
uS là phổ vận tốc gió của thành 
phần rối theo phương x tại độ cao z; 
 1 2coh , ;uu z z f là hàm gắn kết (coherence 
function) của 1,uS z f và 2 ,uS z f . 
22
*
4/3
2
4
,
1
u
u
S z f
f


 (16) 
 *1 0ln /
ak U z
u
z z
 (17) 
1200
10
f
U
 (18) 
 1 21 2 1 2coh , ; exp , ,uu xu
z z
z z f K z z f
L
 
 
 
 (19) 
 1 2 1 2
2
, , zuxu
f c L
K z z f
U z U z
  
 (20) 
Trong đó u* (m/s
2
) là vận tốc nhám bề mặt 
được điều chỉnh từ vận tốc nhám ứng với địa 
hình đồng cỏ u
*1
 với tỉ số u
*
/ u
*1
 được tra 
bảng theo [8] ; k
a
 là hằng số Karman; z
0
(m) là chiều cao nhám bề mặt địa hình; c
zu
là hệ số tác động phương đứng theo phương 
tác động của gió; 10U (m/s2) là vận tốc 
gió trung bình tại độ cao 10m. 
3.2 Hàm phổ S
vv
(z
1
,z
2
,f) 
Phổ gió S
vv
 của thành phần rối v’ được 
cho bởi [2, 9, 11]: 
1 2 1 2
1 2
, , , ,
coh , ;
vv v v
vv
S z z f S z f S z f
z z f
 

 (21) 
 
2
*
5/3
17
,
1 9.5
m
v
T u
S z f
fT
 
 (22) 
m
f z
T
U z

 (23) 
 1 2coh , ;vv z z f tính tương tự như 
 1 2coh , ;uu z z f trong công thức (19). 
4 VÍ DỤ SỐ 
Lý thuyết đề xuất nêu trên được áp dụng 
để tính toán đáp ứng khí động lực học của 
công trình nổi tiếng “Endless Column” hay 
còn gọi là cột Brancusi ở Romania chịu tác 
động của tải trọng gió theo [12] như Hình 2. 
Bảng 1 và Bảng 2 tóm tắt các thông số kết 
cấu kỹ thuật chính. Bảng 3 mô tả các thông 
số của gió tác động và địa hình. 
Hình 2. Cột “Endless Column” Nguồn 
40 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 58 (06/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
Bảng 1. Thông số kết cấu tháp Endless 
Column [12] 
Ký hiệu Giá trị 
L (m) 29 
B (m) 0.9 
m (Tấn) 31 
f
1
 (Hz) 0.513 
f
1
(z) 
1.75
/z L 
Bảng 2. Hệ số khí động học tương ứng góc 
tác động [12] 
Góc tác 
động α 
0
0
 5
0
 45
0
C
D
 1.093 1.087 1.503 
LC -0.0014 -0.159 0.020 
'DC 0 -0.060 0.062 
'LC -1.5360 -1.6904 -0.3966 
Bảng 3. Thông số gió và địa hình [12] 
Ký hiệu Giá trị 
r kg/m3( ) 1.225 
z
0
 (m) 0.05 
U (z) (m/s) 
0.15
( ) /U h z L 
U (h) (m/s) 0 ~ 40 
c
zu
 7 
g
Y
 3.5 
Dựa các công thức 11-13, số liệu từ 
Bảng 1, Bảng 2, Bảng 3, và dùng phương 
pháp số tính toán bằng Matlab, bài báo có 
được kết quả như sau. 
Hình 3 thể hiện chuyển vị tại đỉnh tháp 
theo phương vuông góc của gió (cross-wind) 
tại góc tác động 00, trong đó Y là độ lệch 
chuẩn của chuyển vị theo phương y do gió gây 
ra; ( )Y uu là độ lệch chuẩn của chuyển vị 
theo phương y do thành phần khí rối phương x 
gây ra; ( )Y vv là độ lệch chuẩn của chuyển vị 
theo phương y do thành phần khí rối phương x 
gây ra. Có thể nhận thấy rằng giá trị Y nằm 
gần trùng với giá trị s
Y(vv)
, giá trị s
Y(uu)
bằng 0. Do đó, thành phần khí rối u’ có thể bỏ 
qua khi tính toán chuyển vị s
Y
. 
Hình 4 thể hiện chuyển vị tại đỉnh tháp 
theo phương vuông góc của gió (cross-wind) 
tại góc tác động 50. Có thể nhận thấy rằng giá 
trị s
Y
 nằm gần trùng với giá trị s
Y(vv)
, khi 
U (L) < 25m/ s giá trị s
Y(vv)
 rất nhỏ không 
đáng kể (gần bằng 0) nhưng khi 
U (L) ³ 25m/ s thì giá trị ( )Y uu có giá trị 
lớn. Nhận xét này tương tự ở Hình 5 tại góc 
tác động bằng 450. Điều đó chứng tỏ rằng khi 
vận tốc gió tương đối lớn, thành phần khí rối 
u’ có đóng góp vào chuyển vị s
Y
. Do đó, 
việc bỏ qua phần này như các nghiên cứu 
trước cũng như ở một số tiểu chuẩn chống 
gió sẽ dẫn tới s
Y
 nhỏ hơn khi xét đầy đủ 
các thành phần của dòng rối. Khi đó, việc 
tính toán sẽ gây bất lợi cho kết cấu trong điều 
kiện gió mạnh. 
Hình 3. Độ lệch chuẩn của chuyển vị tại 
đỉnh kết cấu ở góc 00 
Hình 4. Độ lệch chuẩn của chuyển vị tại 
đỉnh kết cấu ở góc 50 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 58 (06/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
41 
Hình 5. Độ lệch của chuyển vị tại đỉnh kết 
cấu ở góc 450 
Hình 6. So sánh giá trị cực đại của chuyển vị 
tại đỉnh kết cấu ở góc 00 giữa nghiên cứu của 
bài báo và theo [12] 
Hình 7. So sánh giá trị cực đại của chuyển vị 
tại đỉnh kết cấu ở góc 450 giữa nghiên cứu 
của bài báo và theo [12] 
Hình 6-7 so sánh chuyển vị tại đỉnh kết 
cấu tại góc 00 và 450 tính theo phương pháp 
của bài báo và nghiên cứu của Solari [12]. 
Điều cần nhấn mạnh là phương pháp sử dụng 
ở nghiên cứu [12] là giống với một số tiêu 
chuẩn hiện hành, trong đó có Eurocode [5] và 
ASCE [4]. Theo đó, đối với chuyển vị 
phương vuông góc với hướng gió 
(cross-wind), thành phần rối theo phương gió 
dọc (u’) bị bỏ qua. Có thể nhận thấy từ 
hình 6-7 rằng chuyển vị tính theo [12] nhỏ 
hơn so với phương pháp của bài báo này. Do 
đó, việc không xét đầy đủ các thành phần của 
dòng rối sẽ gấy bất lợi cho kết cấu. 
5 KẾT LUẬN 
Bài báo đã thiết lập mô hình giải tích để 
phân tích đáp ứng của kết cấu mảnh thẳng 
đứng theo phương vuông góc của gió. Bên 
cạnh thành phần dòng rối vuông góc với 
phương gió, mô hình này có xét đến thành 
phần dòng rối cùng phương với phương gió 
vốn bị bỏ qua trong các nghiên cứu trước. 
Ví dụ số được áp dụng cho một kết cấu 
thực tế đã chỉ ra vai trò rất quan trọng của 
thành phần dòng rối cùng phương với 
phương gió. Đối với kết cấu mảnh thẳng 
đứng, việc bỏ qua thành phần có thể dẫn tới 
những kết quả thiếu chính xác và ảnh hưởng 
bất lợi đối với kết cấu. 
Những nhận xét trên cho thấy rằng cần 
thêm các nghiên cứu để kiểm chứng thêm 
vấn đề mà bài báo đã đặt ra cũng như các tiêu 
chuẩn chống gió đang được sử dụng. 
LỜI CẢM ƠN 
Nghiên cứu này được tài trợ bởi Quỹ 
Phát triển khoa học và công nghệ Quốc gia 
(NAFOSTED) trong đề tài mã số 
107.04-2017.321.
TÀI LIỆU THAM KHẢO 
[1] Y. Kim, K. You, J. You, Across and along-wind responses of tall building, Journal of 
Central South University, 21, pp.4404-4408, 2014. 
[2] G. Solari & F. Tubino, Wind Effects on Buildings and Design of Wind-sensitive Structures, 
International Centre for Mechanical Sciences, pp.137-163, New York, USA, 2007. 
42 
Tạp Chí Khoa Học Giáo Dục Kỹ Thuật Số 58 (06/2020) 
Trường Đại Học Sư Phạm Kỹ Thuật TP. Hồ Chí Minh 
[3] A.G. Davenport, The spectrum of horizontal gustiness near the ground in the high wind, 
Quart J Roy Meteorol Soc, 87, pp.194-211, 1961. 
[4] ASCE, Minimum Design Loads for Buildings and Other Structures, ASCE/SEI 7-10, 2010 
[5] Eurocode 1: Actions on structures - General Actions - Part 1-4: Wind Actions, 1992. 
[6] E. Simiu, Design of buildings for wind. A guide for ASCE 7-10 Standard users and 
designers of special structures, John Wiley & Sons, 2, 2011. 
[7] I. Calotescu & G. Solari, Alongwind load effects on free-standing lattice towers, Journal 
of Wind Engineering and Industrial Aerodynamics, 2016. 
[8] E. Simiu & R. Scanlan, Wind effects on structures - Fundamentals and Application to 
Design, New York: John Wiley & Sons, 3rd ed, 1996. 
[9] G. Solari & G. Picardo, Probabilistic 3-D turbulence modeling for gust buffeting of 
structures, Probabilistic Engineeering Mechanics, 16, pp.73-86, 2001. 
[10] K. D. Nguyen, Phân tích đáp ứng khí động lực học cho kết cấu mảnh thẳng đứng chịu 
tải trọng gió, Luận Văn Thạc Sĩ, trường Đại Học Bách Khoa, Đại học Quốc Gia 
TPHCM, 2020. 
[11] G. Picardo & G. Solari, 3D gust effect factor slender vertical structures, Probabilistic 
Engineeering Mechanics, 17, pp.143-155, 2002. 
[12] G. Solari, Brancusi Endless Column: A Masterpiece of Art and Engineering, Internal 
Journal of High-Rise Building, Vols. 2-3, pp. 193-212, 2013. 
Tác giả chịu trách nhiệm bài viết: 
Nguyễn Huy Cung 
Trường Đại học Công Nghiệp TP.HCM 
Email: nguyenhuycung@iuh.edu.vn