Đánh giá ổn định điện áp trong hệ thống điện truyền tải dùng phương pháp phân tích độ nhạy

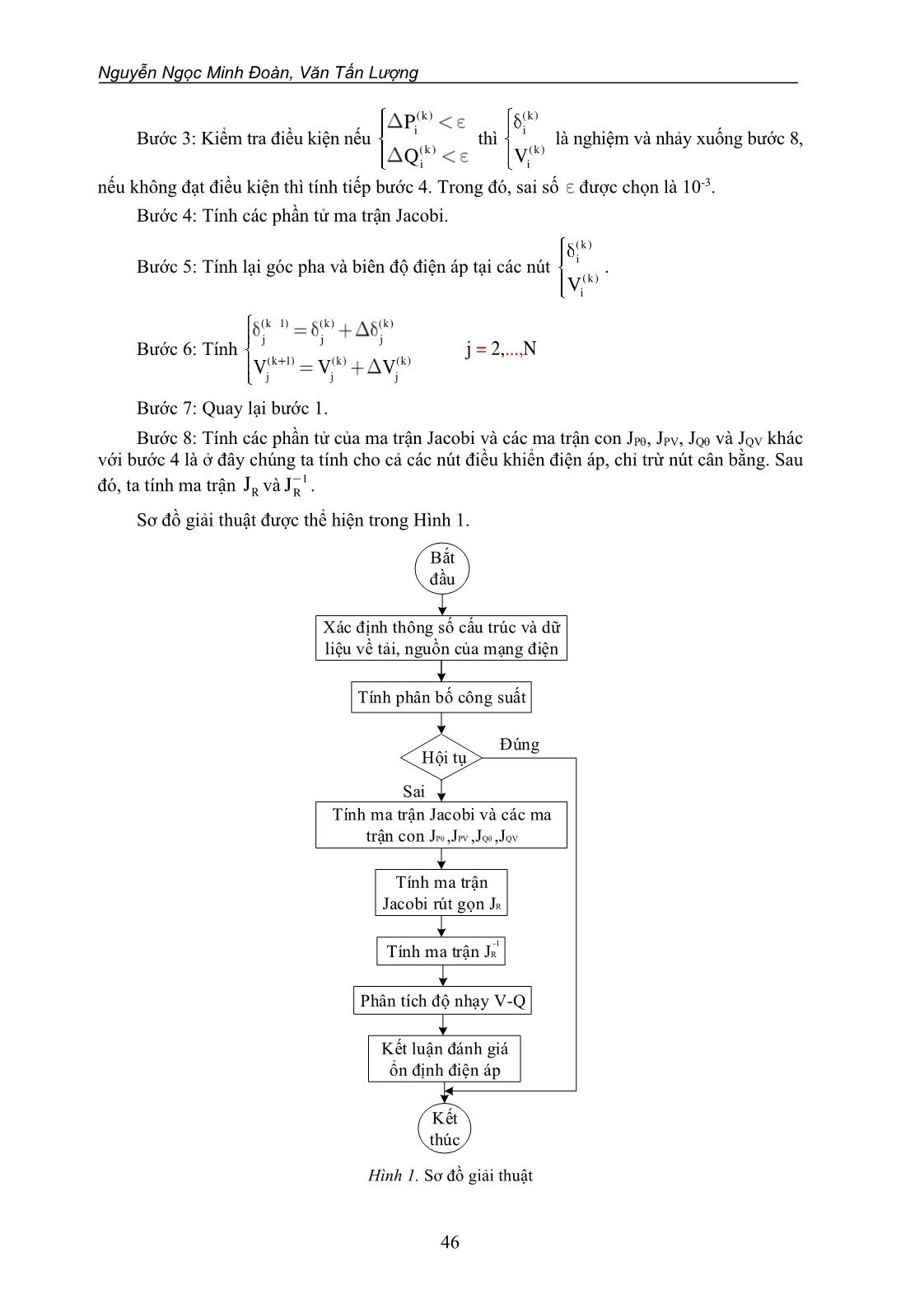
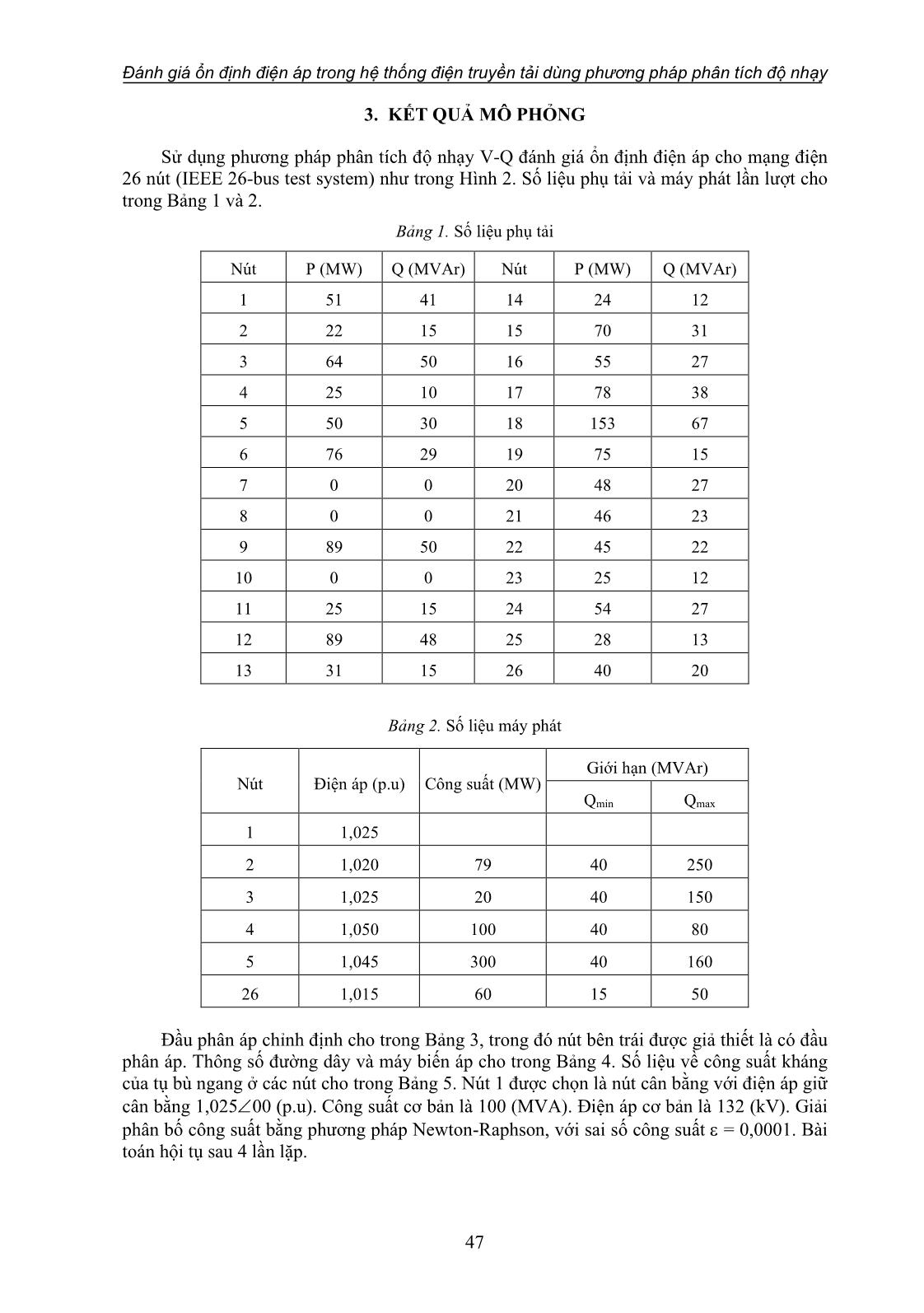
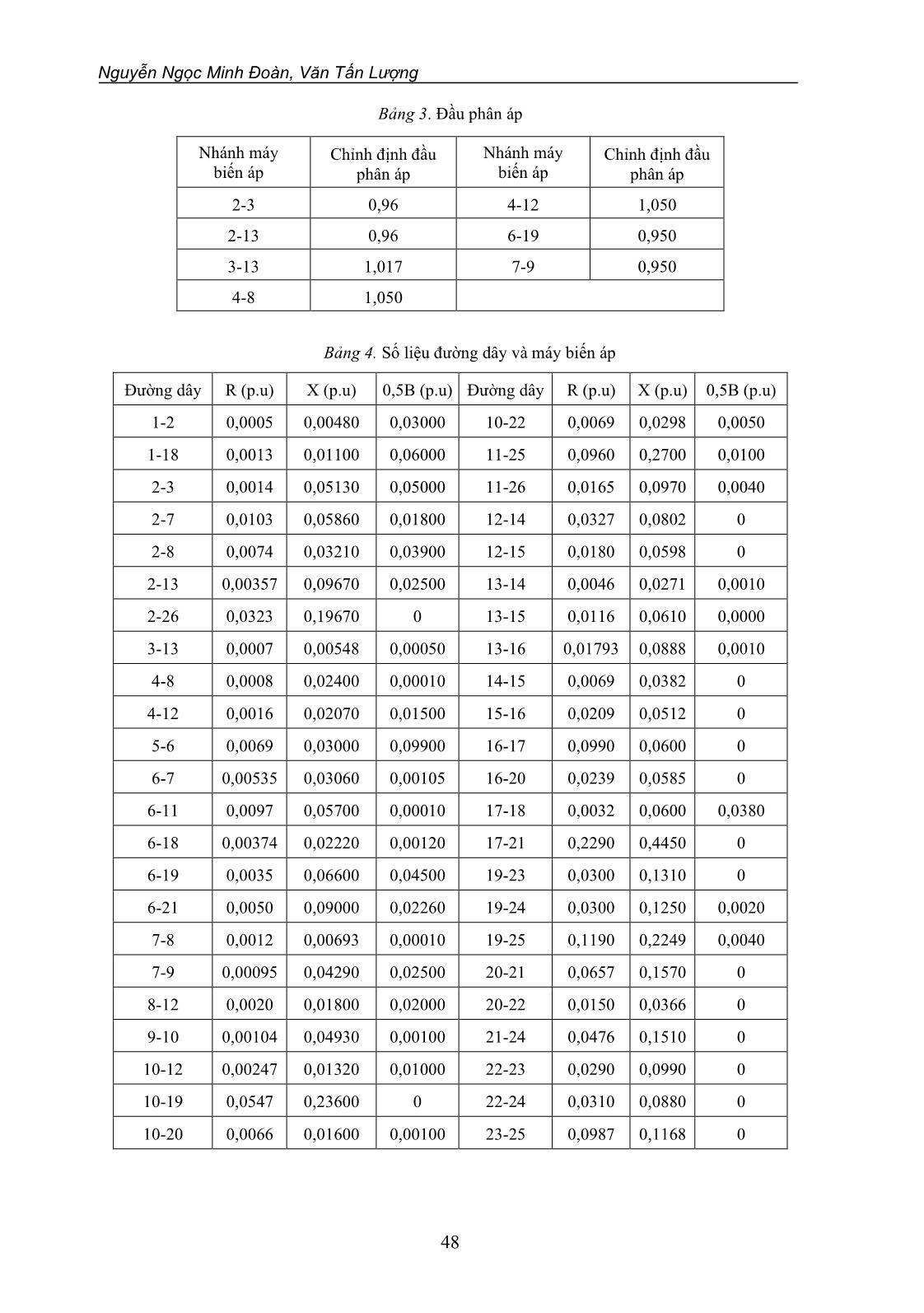
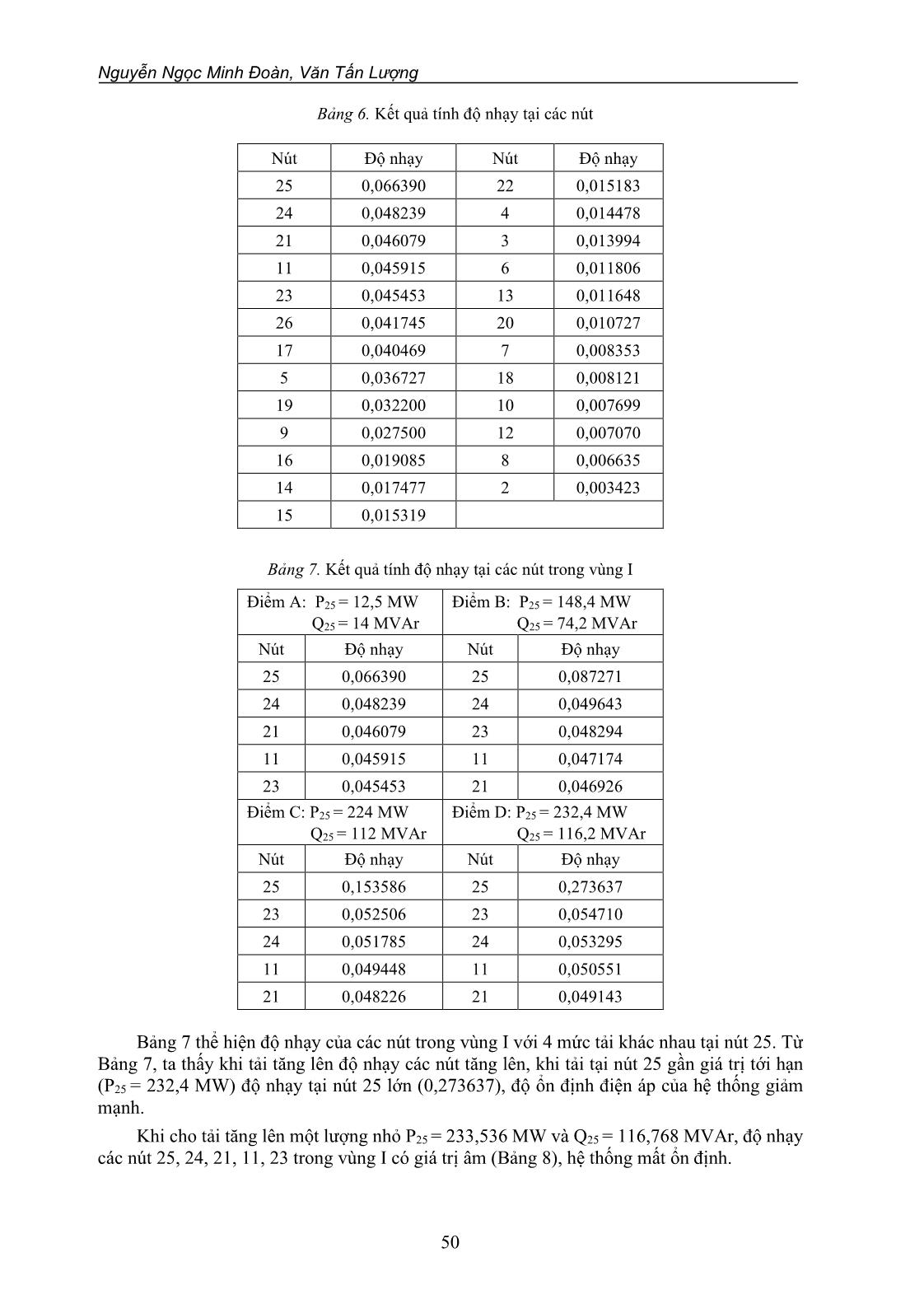
hống là dương thì hệ thống ổn định điện áp, và nếu độ nhạy V-Q của ít nhất một 
nút trong hệ thống là âm thì hệ thống mất ổn định điện áp. Do đó, trong phương pháp phân 
tích độ nhạy V-Q người ta dựa vào đặc điểm này để phân tích đánh giá ổn định điện áp cho hệ 
thống điện. 
Phương trình điện áp – công suất hệ thống trạng thái xác lập ở dạng tuyến tính hóa được 
cho như sau [5-7]: 


 
= 
P PV
Q QV
J JP
J JQ V
 (1) 
Trong đó: 
 P, Q,  và V: lần lượt là độ thay đổi công suất thực tại các nút, độ thay đổi công 
suất phản kháng bơm vào nút, độ thay đổi góc pha của điện áp nút và độ thay đổi biên độ điện 
áp nút; 


P
Q
J
J
PV
QV
J
J
 là ma trận Jacobi gồm 4 ma trận con: JP, JPV, JQ, JQV. 
Trong nghiên cứu này, mô hình phân bố công suất truyền thống được sử dụng để phân 
tích ổn định điện áp. Do đó, ma trận Jacobi trong phương trình (1) cũng giống như ma trận 
Jacobi được sử dụng trong phương pháp lập Newton-Raphson để giải phân bố công suất [5, 10]. 
Sự ổn định điện áp của hệ thống bị ảnh hưởng bởi cả 2 thành phần công suất (P, Q). Tuy 
nhiên, ở mỗi điểm làm việc, chúng ta có thể giữ công suất tác dụng P không đổi và đánh giá 
ổn định điện áp bằng cách xem xét sự thay đổi trong quan hệ giữa Q và V. Mặc dù không xét 
đến sự thay đổi của P, nhưng ảnh hưởng của sự thay đổi phụ tải hệ thống hoặc mức truyền 
công suất cũng được đưa vào tính toán bằng cách nghiên cứu quan hệ giữa Q và V trong các 
điều kiện vận hành với các mức tải công suất P khác nhau. 
Đánh giá ổn định điện áp trong hệ thống điện truyền tải dùng phương pháp phân tích độ nhạy 
45 
Từ (1), ta có hệ phương trình sau: 
P PV
Q QV
P J J V
Q J J V


 = + 
 = + 
 (2) 
Có 2 thông số ảnh hưởng đến độ ổn định điện áp. Đó là công suất tác dụng P và công 
suất phản kháng Q. Để phân tích xem P và Q ảnh hưởng như thế nào đến ổn định điện áp thì 
chúng ta cần giả sử công suất phản kháng hoặc công suất tác dụng bằng hằng số. Trong nghiên 
cứu này, ta cho sai số P = 0 [11, 12]. Do đó, hệ phương trình (2) được viết lại như sau: 
1
P PV
R
J J V
Q J V
−

  = − 
 = 
 (3) 
Trong đó: RJ là ma trận Jacobi rút gọn của hệ thống, được viết lại như sau : 
1
R QV Q P PVJ J J J J
−
 
 = − (4) 
Từ (3), ta có: 
1
RV J Q
− = (5) 
Ma trận 
−1
R
J là ma trận Jacobi V-Q rút gọn. Phần tử đường chéo thứ i của ma trận 
−1
R
J là 
độ nhạy V-Q ở nút thứ i [10]. 
Độ nhạy V-Q ở một nút chính là độ dốc của đường cong Q-V tại điểm làm việc đã cho [11]. 
Nếu độ nhạy V-Q dương cho thấy điểm làm việc là ổn định, độ nhạy càng nhỏ hệ thống càng 
ổn định. Khi độ ổn định giảm, giá trị của độ nhạy sẽ tăng lên và bằng vô cùng khi hệ thống ở 
giới hạn ổn định. Nếu độ nhạy có giá trị âm cho thấy điểm làm việc là không ổn định. 
Để xác định ma trận 
−1
R
J trong việc phân tích ổn định điện áp, trước tiên giải bài toán 
phân bố công suất theo phương pháp lập Newton-Raphson, khi bài toán hội tụ ta tìm được ma 
trận Jacobi tương ứng với các điều kiện vận hành đã cho. Sau đó tìm ma trận Jacobi rút gọn 
theo công thức (4) và cuối cùng tìm được ma trận 
−1
R
J . 
2.2. Sơ đồ thuật toán 
Thuật toán giải phân bố công suất theo phương pháp lập Newton-Raphson và xác định 
ma trận Jacobi rút gọn 
−1
R
J gồm các bước sau: 
Giả thiết (0)
j
 và 
(0)
j
V lần lượt là góc pha và biên độ điện áp ban đầu tại nút j. Xét vòng 
lặp thứ k gồm: 
Bước 1: Dùng các trị số (k)
j
 và 
(k)
j
V , tính công suất tác dụng 
(k )
i
P , và công suất phản 
kháng, 
(k)
i
Q , tại các nút i = 2,,N. 
Bước 2: Tính các sai số (k)
i
P và (k)
i
Q theo công thức sau: 
(k) (k)
i o i i
(k) (k)
i o i i
P P P
Q Q Q
−
−
 = −
 = − 
 (6) 
Nguyễn Ngọc Minh Đoàn, Văn Tấn Lượng 
46 
Bước 3: Kiểm tra điều kiện nếu 
(k)
i
(k)
i
P
Q
 thì 
(k)
i
(k)
i
V
 là nghiệm và nhảy xuống bước 8, 
nếu không đạt điều kiện thì tính tiếp bước 4. Trong đó, sai số được chọn là 10-3. 
Bước 4: Tính các phần tử ma trận Jacobi. 
Bước 5: Tính lại góc pha và biên độ điện áp tại các nút 
(k)
i
(k)
i
V
. 
Bước 6: Tính 
(k 1) (k) (k)
j j j
(k 1) (k) (k)
j j j
 j 2, N
V V V
= ..., 
Bước 7: Quay lại bước 1. 
Bước 8: Tính các phần tử của ma trận Jacobi và các ma trận con JP, JPV, JQ và JQV khác 
với bước 4 là ở đây chúng ta tính cho cả các nút điều khiển điện áp, chỉ trừ nút cân bằng. Sau 
đó, ta tính ma trận 
R
J và 1
R
J . 
Sơ đồ giải thuật được thể hiện trong Hình 1. 
Bắt 
đầu
Xác định thông số cấu trúc và dữ 
liệu về tải, nguồn của mạng điện 
Tính phân bố công suất
Tính ma trận Jacobi và các ma 
trận con JPθ ,JPV ,JQθ ,JQV
Tính ma trận 
Jacobi rút gọn JR
Tính ma trận JR
-1
Phân tích độ nhạy V-Q
Kết luận đánh giá 
ổn định điện áp
Kết 
thúc
Hội tụ
Đúng
Sai
Hình 1. Sơ đồ giải thuật 
Đánh giá ổn định điện áp trong hệ thống điện truyền tải dùng phương pháp phân tích độ nhạy 
47 
3. KẾT QUẢ MÔ PHỎNG 
Sử dụng phương pháp phân tích độ nhạy V-Q đánh giá ổn định điện áp cho mạng điện 
26 nút (IEEE 26-bus test system) như trong Hình 2. Số liệu phụ tải và máy phát lần lượt cho 
trong Bảng 1 và 2. 
Bảng 1. Số liệu phụ tải 
Nút P (MW) Q (MVAr) Nút P (MW) Q (MVAr) 
1 51 41 14 24 12 
2 22 15 15 70 31 
3 64 50 16 55 27 
4 25 10 17 78 38 
5 50 30 18 153 67 
6 76 29 19 75 15 
7 0 0 20 48 27 
8 0 0 21 46 23 
9 89 50 22 45 22 
10 0 0 23 25 12 
11 25 15 24 54 27 
12 89 48 25 28 13 
13 31 15 26 40 20 
Bảng 2. Số liệu máy phát 
Nút Điện áp (p.u) Công suất (MW) 
Giới hạn (MVAr) 
Qmin Qmax 
1 1,025 
2 1,020 79 40 250 
3 1,025 20 40 150 
4 1,050 100 40 80 
5 1,045 300 40 160 
26 1,015 60 15 50 
Đầu phân áp chỉnh định cho trong Bảng 3, trong đó nút bên trái được giả thiết là có đầu 
phân áp. Thông số đường dây và máy biến áp cho trong Bảng 4. Số liệu về công suất kháng 
của tụ bù ngang ở các nút cho trong Bảng 5. Nút 1 được chọn là nút cân bằng với điện áp giữ 
cân bằng 1,02500 (p.u). Công suất cơ bản là 100 (MVA). Điện áp cơ bản là 132 (kV). Giải 
phân bố công suất bằng phương pháp Newton-Raphson, với sai số công suất  = 0,0001. Bài 
toán hội tụ sau 4 lần lặp. 
Nguyễn Ngọc Minh Đoàn, Văn Tấn Lượng 
48 
Bảng 3. Đầu phân áp 
Nhánh máy 
biến áp 
Chỉnh định đầu 
phân áp 
Nhánh máy 
biến áp 
Chỉnh định đầu 
phân áp 
2-3 0,96 4-12 1,050 
2-13 0,96 6-19 0,950 
3-13 1,017 7-9 0,950 
4-8 1,050 
Bảng 4. Số liệu đường dây và máy biến áp 
Đường dây R (p.u) X (p.u) 0,5B (p.u) Đường dây R (p.u) X (p.u) 0,5B (p.u) 
1-2 0,0005 0,00480 0,03000 10-22 0,0069 0,0298 0,0050 
1-18 0,0013 0,01100 0,06000 11-25 0,0960 0,2700 0,0100 
2-3 0,0014 0,05130 0,05000 11-26 0,0165 0,0970 0,0040 
2-7 0,0103 0,05860 0,01800 12-14 0,0327 0,0802 0 
2-8 0,0074 0,03210 0,03900 12-15 0,0180 0,0598 0 
2-13 0,00357 0,09670 0,02500 13-14 0,0046 0,0271 0,0010 
2-26 0,0323 0,19670 0 13-15 0,0116 0,0610 0,0000 
3-13 0,0007 0,00548 0,00050 13-16 0,01793 0,0888 0,0010 
4-8 0,0008 0,02400 0,00010 14-15 0,0069 0,0382 0 
4-12 0,0016 0,02070 0,01500 15-16 0,0209 0,0512 0 
5-6 0,0069 0,03000 0,09900 16-17 0,0990 0,0600 0 
6-7 0,00535 0,03060 0,00105 16-20 0,0239 0,0585 0 
6-11 0,0097 0,05700 0,00010 17-18 0,0032 0,0600 0,0380 
6-18 0,00374 0,02220 0,00120 17-21 0,2290 0,4450 0 
6-19 0,0035 0,06600 0,04500 19-23 0,0300 0,1310 0 
6-21 0,0050 0,09000 0,02260 19-24 0,0300 0,1250 0,0020 
7-8 0,0012 0,00693 0,00010 19-25 0,1190 0,2249 0,0040 
7-9 0,00095 0,04290 0,02500 20-21 0,0657 0,1570 0 
8-12 0,0020 0,01800 0,02000 20-22 0,0150 0,0366 0 
9-10 0,00104 0,04930 0,00100 21-24 0,0476 0,1510 0 
10-12 0,00247 0,01320 0,01000 22-23 0,0290 0,0990 0 
10-19 0,0547 0,23600 0 22-24 0,0310 0,0880 0 
10-20 0,0066 0,01600 0,00100 23-25 0,0987 0,1168 0 
Đánh giá ổn định điện áp trong hệ thống điện truyền tải dùng phương pháp phân tích độ nhạy 
49 
Bảng 5. Số liệu công suất kháng của tụ bù ngang 
Nút MVAr Nút MVAr 
1 4 11 1,5 
4 2 12 2 
5 5 15 0,5 
6 2 19 5 
GG
G
G
G
17
21
23
2022
24
15
101925
11
9 12
18
26
5
6
7
1614
4
3
13
2
8
1
I
Hình 2. Sơ đồ mạng điện [7] 
Kết quả tính độ nhạy tại các nút thể hiện trong Bảng 6. Dựa vào kết quả tính toán ta thấy 
các giá trị của độ nhạy V-Q đều dương, do đó hệ thống điện ở trên là ổn định. Trong đó, nút 
số 25 có độ ổn định kém nhất. 
Khảo sát ổn định điện áp của hệ thống khi thay đổi tải trong vùng I, như trong Hình 2. Bằng 
cách tăng từ từ tải nút 25 từ 0 đến giá trị tới hạn (hệ số công suất không đổi, cos = 0,8944), ta 
được đường cong P-V tại nút 25 như Hình 3. 
Đ
iệ
n
 á
p
 (
p
.u
)
Công suất (MW)
A
B
C
D
Hình 3. Đường cong P-V tại nút 25, với cos = 0,8944 
Nguyễn Ngọc Minh Đoàn, Văn Tấn Lượng 
50 
 Bảng 6. Kết quả tính độ nhạy tại các nút 
Nút Độ nhạy Nút Độ nhạy 
25 0,066390 22 0,015183 
24 0,048239 4 0,014478 
21 0,046079 3 0,013994 
11 0,045915 6 0,011806 
23 0,045453 13 0,011648 
26 0,041745 20 0,010727 
17 0,040469 7 0,008353 
5 0,036727 18 0,008121 
19 0,032200 10 0,007699 
9 0,027500 12 0,007070 
16 0,019085 8 0,006635 
14 0,017477 2 0,003423 
15 0,015319 
Bảng 7. Kết quả tính độ nhạy tại các nút trong vùng I 
Điểm A: P25 = 12,5 MW 
 Q25 = 14 MVAr 
Điểm B: P25 = 148,4 MW 
 Q25 = 74,2 MVAr 
Nút Độ nhạy Nút Độ nhạy 
25 0,066390 25 0,087271 
24 0,048239 24 0,049643 
21 0,046079 23 0,048294 
11 0,045915 11 0,047174 
23 0,045453 21 0,046926 
Điểm C: P25 = 224 MW 
 Q25 = 112 MVAr 
Điểm D: P25 = 232,4 MW 
 Q25 = 116,2 MVAr 
Nút Độ nhạy Nút Độ nhạy 
25 0,153586 25 0,273637 
23 0,052506 23 0,054710 
24 0,051785 24 0,053295 
11 0,049448 11 0,050551 
21 0,048226 21 0,049143 
Bảng 7 thể hiện độ nhạy của các nút trong vùng I với 4 mức tải khác nhau tại nút 25. Từ 
Bảng 7, ta thấy khi tải tăng lên độ nhạy các nút tăng lên, khi tải tại nút 25 gần giá trị tới hạn 
(P25 = 232,4 MW) độ nhạy tại nút 25 lớn (0,273637), độ ổn định điện áp của hệ thống giảm 
mạnh. 
Khi cho tải tăng lên một lượng nhỏ P25 = 233,536 MW và Q25 = 116,768 MVAr, độ nhạy 
các nút 25, 24, 21, 11, 23 trong vùng I có giá trị âm (Bảng 8), hệ thống mất ổn định. 
Đánh giá ổn định điện áp trong hệ thống điện truyền tải dùng phương pháp phân tích độ nhạy 
51 
Bảng 8. Kết quả tính độ nhạy tại các nút trong vùng I (hệ thống mất ổn định) 
Nút Độ nhạy Nút Độ nhạy 
25 -0,045842 11 -0,001925 
23 -0,028734 21 -0,000542 
24 -0,007316 
4. KẾT LUẬN VÀ THẢO LUẬN 
Trong bài báo, phương pháp phân tích ổn định điện áp dựa trên cơ sở phân tích độ nhạy 
V-Q của ma trận Jacobi được thành lập từ bài toán phân bố công suất Newton-Raphson đã 
được nghiên cứu. Với phương pháp này, đầu tiên bài toán phân bố công suất Newton-Raphson 
đã được áp dụng, từ đó các ma trận con của ma trận Jacobi được tính toán. Sau đó, phương 
pháp phân tích độ nhạy V-Q đã được thực hiện. Cuối cùng, mạng IEEE- 26 nút được áp dụng 
để kiểm chứng tính khả khi của phương pháp. 
Với phương pháp phân tích ổn định điện áp dựa trên cơ sở phân tích độ nhạy V-Q như 
trên, những ưu và khuyết điểm của phương pháp được liệt kê như sau: 
Việc giải bài toán phân bố công suất theo phương pháp Newton-Raphson thì ta nhận thấy 
rằng bài toán sẽ hội tụ với số vòng lặp ít (cụ thể trong mạng ta giải bài toán phân bố công suất 
với số vòng lặp là 4), do đó sai số công suất sẽ không đáng kể. Do vậy, kết quả sẽ có tính chính 
xác cao. 
Phương pháp phân tích độ nhạy có thể đưa ra được kết quả đánh giá sự ổn định điện áp 
một cách khái quát của các nút trong hệ thống. Từ đó, ta có thể biết được là hệ thống có ổn 
định hay không. Trong phương pháp này, độ nhạy của các nút càng cao thì hệ thống càng dễ 
mất ổn định. Hệ thống sẽ bị mất ổn định nếu một trong số các nút của hệ thống có độ nhạy âm. 
Tuy nhiên, nếu chỉ dựa vào độ nhạy của hệ thống thì ta không biết được là hệ thống đã 
tiến tới điểm làm việc tới hạn hay chưa. Do vậy mà ta vẫn không biết được chính xác hệ thống 
đang ở mức nào so với ranh giới mất ổn định để từ đó ta có những giải pháp thích hợp hơn. 
TÀI LIỆU THAM KHẢO 
1. Begovic M., Fulton D., Gonzalez M.R., Goossens J., Guro E.A., Haas R.W., 
Henville C.F., Manchur G., Michel G.L., Pastore R.C., Postforoosh J., Schmitt G.L., 
Williams J.B., Zimmerman K., Burzese A.A - Summary of “System protection and 
voltage stability”, IEEE Transactions on Power Delivery 10 (2) (1995) 631-663. 
2. Ben-Kilani K. and Elleuch M. - Structural analysis of voltage stability in power systems 
integrating wind power, IEEE Transactions on Power Systems 28 (4) (2013) 3785-3794. 
3. Vittal E., O’Malley M., and Keane K. - A steady-state voltage stability analysis of power 
systems with high penetrations of wind IEEE Transactions on Power Systems 25 (1) 
(2013) 433-442. 
4. Zabaiou T., Dessaint L.-A. and Kamwa I. - Preventive control approach for voltage 
stability improvement using voltage stability constrained optimal power flow based on 
static line voltage stability indices, IET Generation, Transmission & Distribution 8 (5) 
(2014) 924-934. 
5. Byung Ha Lee, Kwang Y. Lee - A study on voltage collapse mechanism in electric 
power systems, IEEE Transactions on Power System 6 (3) (1991) 966-974. 
Nguyễn Ngọc Minh Đoàn, Văn Tấn Lượng 
52 
6. Gao B., Morison G. K., Kundar P. - Voltage stability evaluation using modal analysis, 
IEEE Transactions on Power System 7 (4) (1992) 1529-1542. 
7. Hồ Văn Hiến - Hệ thống điện Truyền tải và Phân Phối, Nhà xuất bản Đại học Quốc gia 
Thành phố Hồ Chí Minh (2005). 
8. Aghatehrani R. and Kavasseri R. - Reactive power management of a DFIG wind system 
in microgrids based on voltage sensitivity analysis, IEEE Transactions on Sustainable 
Energy 2 (4) (2011) 451-458. 
9. Gao Yajing, Yang Wenhai, Zhu Jing, Ren Jiafeng, Li Peng - Evaluating the effect of 
distributed generation on power supply capacity in active distribution system based on 
sensitivity analysis, Energies 10 (10) (1473) (2017) 1-14. 
10. Hadi Saadat - Power System Analysis, McGraw-Hill International Editions (1999). 
11. Jia-Hui Wu, Hai-Yun Wang, Wei-Qing Wang & Qiang Zhang - A comprehensive 
evaluation approach for static voltage stability analysis in electric power grids, Electric 
Power Components and Systems 47 (6-7) (2019) 573-588. 
12. Prabha Kundur - Power system stability and control, McGraw-Hill International 
Editions (1994). 
ABSTRACT 
VOLTAGE STABILITY ASSESSMENT IN POWER TRANSMISSION SYSTEM 
USING SENSITIVITY ANALYSIS METHOD 
Nguyen Ngoc Minh Doan, Van Tan Luong* 
Ho Chi Minh City University of Food Industry 
*Email: luongvt@hufi.edu.vn 
In the paper, the V-Q sensitivity analysis based on Newton-Raphson method is applied 
for the voltage stability analysis. The proposed method gives the voltage stability-related 
information in the whole system and clearly identifies the areas that have the potential 
problems. The effectiveness of the proposed method is verified by Matlab-based simulation 
results for IEEE-26 node network. 
Keywords: Power system, voltage stability, sensitivity analysis, power flow.