Current controller design based on FPGA

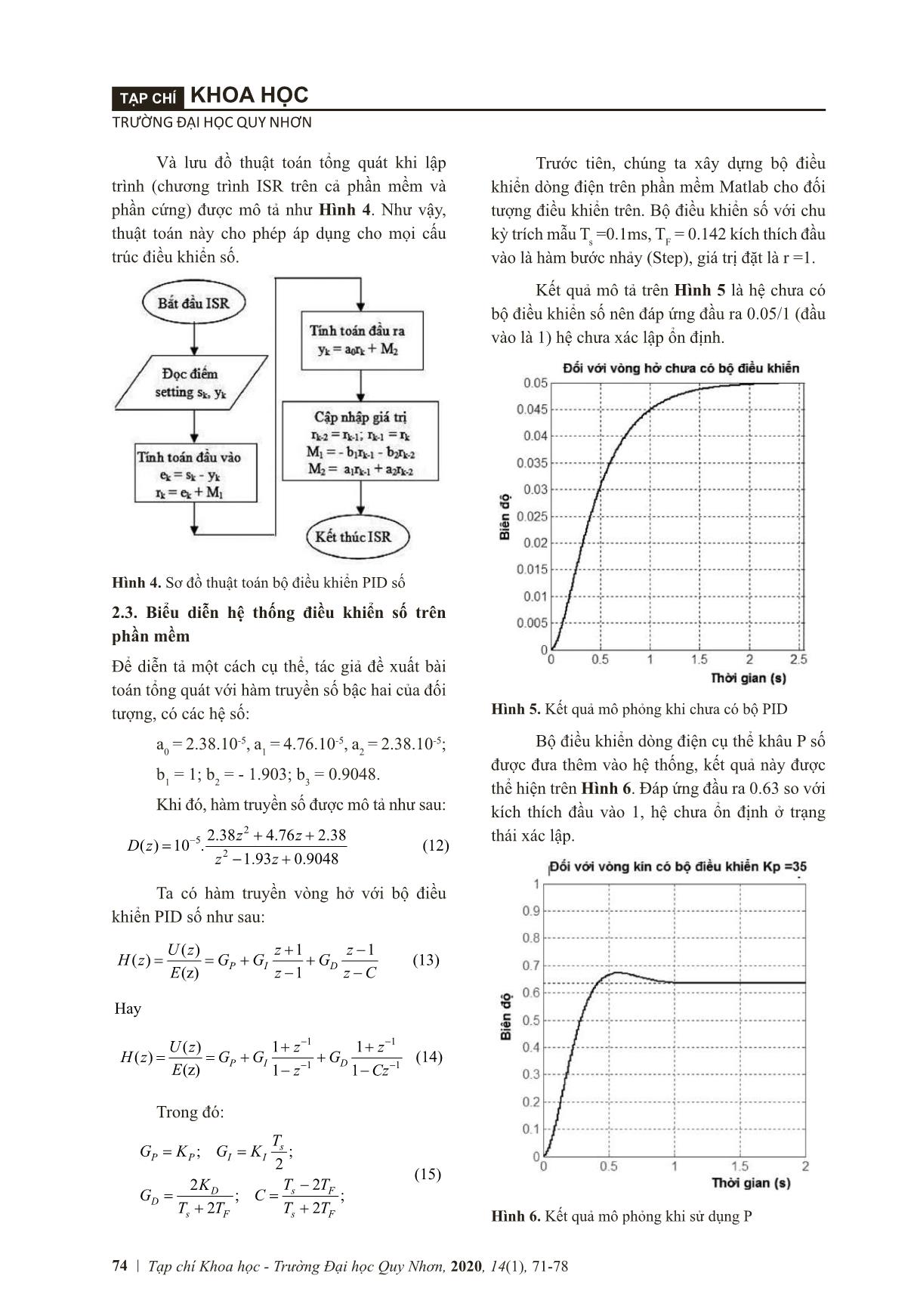
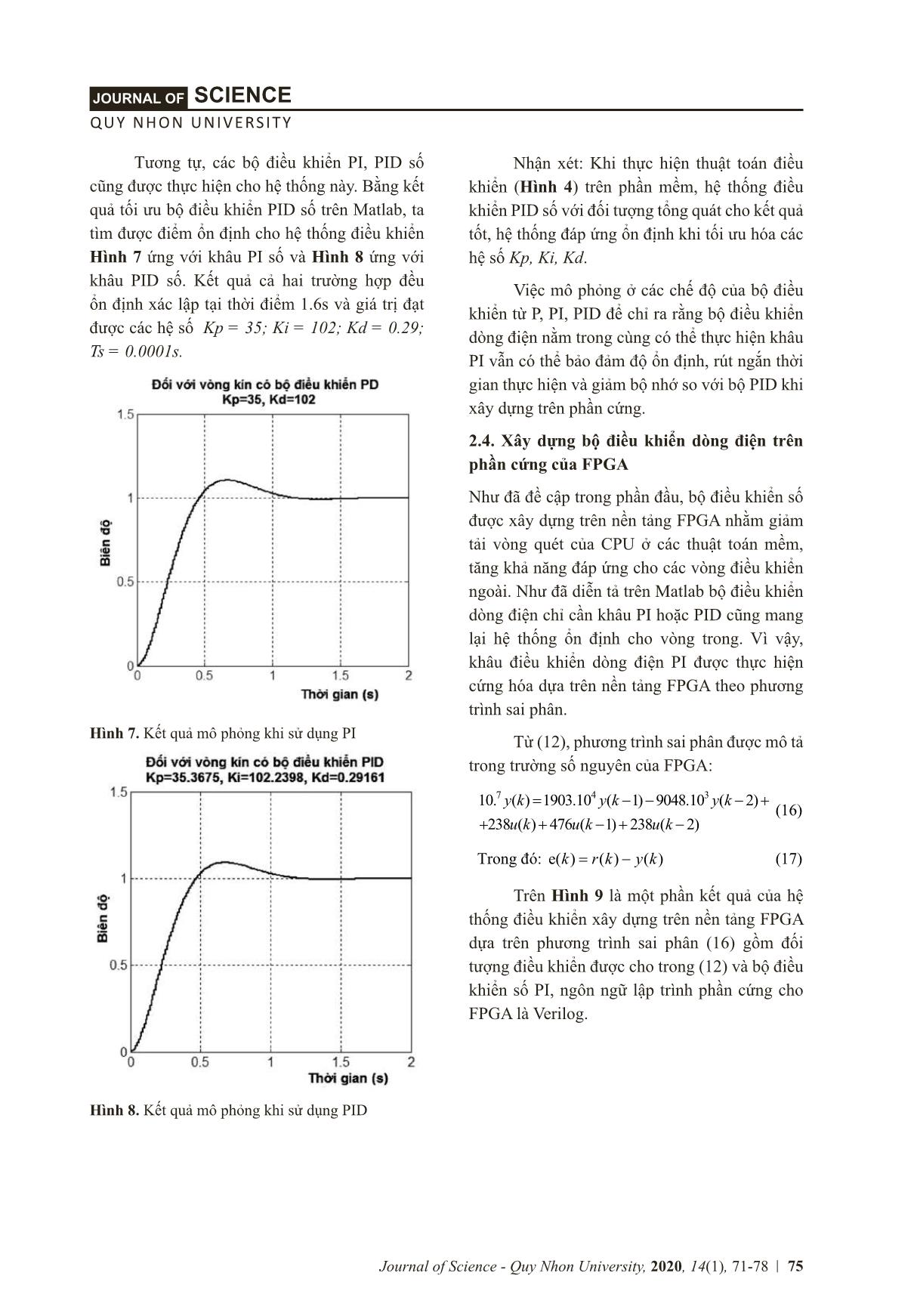
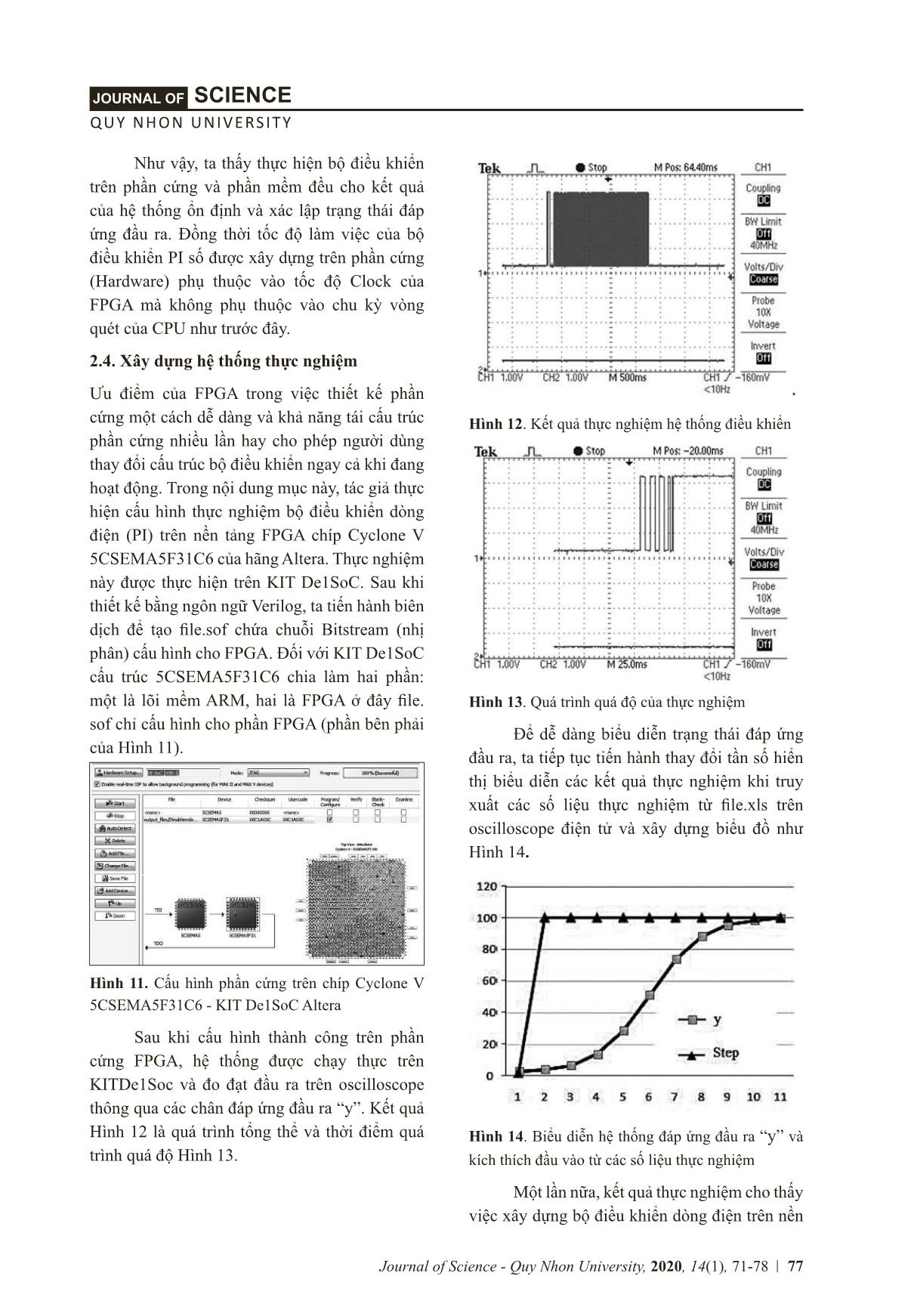
 trị đầu vào 
đặt r = 100. Nếu so sánh với việc mô phỏng trên 
Matlab thì số chu kỳ để đạt được giá trị xác lập 
ổn định thì ở đây đáp ứng nhanh hơn nhiều. Điều 
đó nhờ vào hoạt động độc lập của bộ điều khiển 
được thiết kế cứng, chúng không phụ thuộc vào 
các vòng quét của CPU. 
Trước tiên, chúng ta xây dựng bộ điều 
khiển dòng điện trên phần mềm Matlab cho đối 
tượng điều khiển trên. Bộ điều khiển số với chu 
kỳ trích mẫu T
s
 =0.1ms, T
F
 = 0.142 kích thích đầu 
vào là hàm bước nhảy (Step), giá trị đặt là r =1.
Kết quả mô tả trên Hình 5 là hệ chưa có 
bộ điều khiển số nên đáp ứng đầu ra 0.05/1 (đầu 
vào là 1) hệ chưa xác lập ổn định.
Hình 5. Kết quả mô phỏng khi chưa có bộ PID
Bộ điều khiển dòng điện cụ thể khâu P số 
được đưa thêm vào hệ thống, kết quả này được 
thể hiện trên Hình 6. Đáp ứng đầu ra 0.63 so với 
kích thích đầu vào 1, hệ chưa ổn định ở trạng 
thái xác lập.
Hình 6. Kết quả mô phỏng khi sử dụng P
1 1
1 1
( )( )
( )
− −
− −P I
z z zz
z z
 ( ) 
r : 
; ;
; ;
s
P P I I
s F
s F s F
 ( ) ( ) 
r ti , t i i 
 i tr tl i t 
i i tr . i i s i trí 
 s . s, F . í t í l 
 ( t ), i trị t l r . 
t t tr ì l i 
i s r . / ( l ) 
 l ị . 
ì . ết ả i c a c I 
 i i i t s 
 t t , t t i 
tr ì . r . s i í 
t í , ị tr t i 
l . 
ì . ết ả i s 
 t , i i I, I s 
 t i t . t 
t i i i I s tr tl , t tì 
 i ị t i i ì 
 i I s ì i 
I s . t i tr ị 
 l t i t i i . s i trị t 
 s ; i ; . ; s 
. s. 
ì . ết ả i s I 
ì . ết ả i s I 
 t: i t i t t t i i 
( ì ) tr , t i i 
I s i i t t t t t t, 
 t ị i t i s 
, i, . 
i i i t 
, I, I ỉ r r i i i 
 tr t t i I 
t ị , r t t i i t 
i i s i I i 
tr . 
. . i i i t 
 tr , i i s 
 tr t i 
t i t t t t , 
t i i 
i. i t tr tl i i 
 i ỉ I I 
l i t ị tr . ì , 
i i i I t i 
 tr t t trì s i 
. 
 ( ), trì s i t tr 
tr s : 
7 4 3. ( ) . ( ) . ( )
( ) ( ) ( )
 ( ) 
r : ( ) ( ) ( )r ( ) 
r ì l t t t 
i i tr t 
tr trì s i ( ) i t 
i i tr ( ) i i 
s I, l trì l 
ril . 
ì . t ầ cấ tr c ệ iề iể s I s â trê ề tả 
 i t i i i 
i i s I tr , t i ti 
 t tr 
l i lt r i l 
, s (tr t t t 
 l s), i trị t r (s 
i t i tr í ). t ỉ r tr 
ì ( -t t , l l ) t 
t ị l t i i s i i trị 
 r l t i trị 
t r . s s i i tr 
tl t ì s t i trị l 
 ị t ì i . i 
 t l i i 
 t i t , t 
 t . 
75
QUY NHON UNIVERSITY
SCIENCEJOURNAL OF
Journal of Science - Quy Nhon University, 2020, 14(1), 71-78
Tương tự, các bộ điều khiển PI, PID số 
cũng được thực hiện cho hệ thống này. Bằng kết 
quả tối ưu bộ điều khiển PID số trên Matlab, ta 
tìm được điểm ổn định cho hệ thống điều khiển 
Hình 7 ứng với khâu PI số và Hình 8 ứng với 
khâu PID số. Kết quả cả hai trường hợp đều 
ổn định xác lập tại thời điểm 1.6s và giá trị đạt 
được các hệ số Kp = 35; Ki = 102; Kd = 0.29; 
Ts = 0.0001s.
Hình 7. Kết quả mô phỏng khi sử dụng PI
Hình 8. Kết quả mô phỏng khi sử dụng PID
Nhận xét: Khi thực hiện thuật toán điều 
khiển (Hình 4) trên phần mềm, hệ thống điều 
khiển PID số với đối tượng tổng quát cho kết quả 
tốt, hệ thống đáp ứng ổn định khi tối ưu hóa các 
hệ số Kp, Ki, Kd.
Việc mô phỏng ở các chế độ của bộ điều 
khiển từ P, PI, PID để chỉ ra rằng bộ điều khiển 
dòng điện nằm trong cùng có thể thực hiện khâu 
PI vẫn có thể bảo đảm độ ổn định, rút ngắn thời 
gian thực hiện và giảm bộ nhớ so với bộ PID khi 
xây dựng trên phần cứng.
2.4. Xây dựng bộ điều khiển dòng điện trên 
phần cứng của FPGA
Như đã đề cập trong phần đầu, bộ điều khiển số 
được xây dựng trên nền tảng FPGA nhằm giảm 
tải vòng quét của CPU ở các thuật toán mềm, 
tăng khả năng đáp ứng cho các vòng điều khiển 
ngoài. Như đã diễn tả trên Matlab bộ điều khiển 
dòng điện chỉ cần khâu PI hoặc PID cũng mang 
lại hệ thống ổn định cho vòng trong. Vì vậy, 
khâu điều khiển dòng điện PI được thực hiện 
cứng hóa dựa trên nền tảng FPGA theo phương 
trình sai phân.
Từ (12), phương trình sai phân được mô tả 
trong trường số nguyên của FPGA: 
Trên Hình 9 là một phần kết quả của hệ 
thống điều khiển xây dựng trên nền tảng FPGA 
dựa trên phương trình sai phân (16) gồm đối 
tượng điều khiển được cho trong (12) và bộ điều 
khiển số PI, ngôn ngữ lập trình phần cứng cho 
FPGA là Verilog.
4 
1 1
1 1
( ) 1 1( )
(z) 1 1
− −
− −
+ +
= = + +
− −P I D
U z z zH z G G G
E z Cz
 (14) 
Trong đó: 
; ;
2
22 ; ;
2 2
= =
−
= =
+ +
s
P P I I
s FD
D
s F s F
TG K G K
T TKG C
T T T T
 (15) (15) 
Trước tiên, chúng ta xây dựng bộ điều khiển 
dòng điện trên phần mềm Matlab cho đối tượng 
điều khiển trên. Bộ điều khiển số với chu kỳ trích 
mẫu Ts =0.1ms, TF = 0.142 kích thích đầu vào là 
hàm bước nhảy (Step), giá trị đặt là r =1. 
Kết quả mô tả trên Hình 5 là hệ chưa có bộ điều 
khiển số nên đáp ứng đầu ra 0.05/1 (đầu vào là 1) 
hệ chưa xác lập ổn định. 
Hình 5. Kết quả mô phỏng khi chưa có bộ PID 
Bộ điều khiển dòng điện cụ thể khâu P số được 
đưa thêm vào hệ thống, kết quả này được thể hiện 
trên Hình 6. Đáp ứng đầu ra 0.63 so với kích 
thích đầu vào 1, hệ chưa ổn định ở trạng thái xác 
lập. 
Hình 6. Kết quả mô phỏng khi sử dụng P 
Tương tự, các bộ điều khiển PI, PID số cũng 
được thực hiện cho hệ thống này. Bằng kết quả 
tối ưu bộ điều khiển PID số trên Matlab, ta tìm 
được điểm ổn định cho hệ thống điều khiển Hình 
7 ứng với khâu PI số và Hình 8 ứng với khâu 
PID số. Kết quả cả hai trường hợp đều ổn định 
xác lập tại thời điểm 1.6s và giá trị đạt được các 
hệ số Kp = 35; Ki = 102; Kd = 0.29; Ts = 
0.0001s. 
Hình 7. Kết quả mô phỏng khi sử dụng PI 
Hình 8. Kết quả mô phỏng khi sử dụng PID 
Nhận xét: Khi thực hiện thuật toán điều khiển 
(Hình 4) trên phần mềm hệ, thống điều khiển 
PID số với đối tượng tổng quát cho kết quả tốt,
hệ thống đáp ứng ổn định khi tối ưu hoá các hệ số 
Kp, Ki, Kd. 
Việc mô phỏng ở các chế độ của bộ điều khiển từ 
P, PI, PID để chỉ ra rằng bộ điều khiển dòng điện 
nằm trong cùng có thể thực hiện khâu PI vẫn có 
thể bảo đảm độ ổn định, rút ngắn thời gian thực 
hiện và giảm bộ nhớ so với bộ PID khi xây dựng 
trên phần cứng. 
2.4. Xây dựng bộ điều khiển dòng điện trên 
phần cứng của FPGA 
Như đã đề cập trong phần đầu, bộ điều khiển số 
được xây dựng trên nền tảng FPGA nhằm giảm 
tải vòng quét của CPU ở các thuật toán mềm, 
tăng khả năng đáp ứng cho các vòng điều khiển 
ngoài. Như đã diễn tả trên Matlab bộ điều khiển 
dòng điện chỉ cần k âu PI hoặc PID cũng mang
lại hệ thống ổn định cho vòng trong. Vì vậy, khâu 
điều khiển dòng điện PI được thực hiện cứng hoá 
dựa trên nền tảng FPGA theo phương trình sai 
phân. 
Từ (12), phương trình sai phân được mô tả trong
trường số nguyên của FPGA: 
7 4 310. ( ) 1903.10 ( 1) 9048.10 ( 2)
238 ( ) 476 ( 1) 238 ( 2)
= − − − +
+ + − + −
y k y k y k
u k u k u k
 (16) 
Trong đó: e( ) ( ) ( )= −k r k y k (17) 
Trên Hình 9 là một phần kết quả của hệ thống 
điều khiển xây dựng trên nền tảng FPGA dựa 
trên phương trình sai phân (16) gồm đối tượng 
điều khiển được cho trong (12) và bộ điều khiển 
số PI, ngôn ngữ lập trình phần cứng cho FPGA là 
Verilog. 
Hình 9. Một phần cấu trúc hệ điều khiển sử dụng bộ PI số xây dựng trên nền tảng FPGA 
Sau khi xây dựng hệ thống điều khiển với khâu 
điều khiển số PI cứng hoá trên FPGA, tác giả tiến 
hành mô phỏng kết quả trên phần mềm 
ModelSim của Altera với chu kỳ CLOCK là 
0,1ms (trong thực tế hệ thống này cho phép mô 
phỏng lên đến 1ps), giá trị đặt r = 100 (số nguyên 
khi thực hiện trên chíp). Kết quả được chỉ ra trên 
Hình 10 (a-tổng thể, b là phóng lớn) cho thấy hệ 
thống ổn định xác lập ở thời gian 41ms với giá trị 
đầu ra xác lập y = 100 tương ứng giá trị đầu vào 
đặt r = 100. Nếu so sánh với việc mô phỏng trên 
Matlab thì số chu kỳ để đạt được giá trị xác lập 
ổn định thì ở đây đáp ứng nhanh hơn nhiều. Điều 
đó nhờ vào hoạt động độc lập của bộ điều khiển 
được thiết kế cứng, chúng không phụ thuộc vào 
các vòng quét của CPU. 
76
TRƯỜNG ĐẠI HỌC QUY NHƠN
KHOA HỌCTẠP CHÍ
Tạp chí Khoa học - Trường Đại học Quy Nhơn, 2020, 14(1), 71-78
Sau khi xây dựng hệ thống điều khiển với 
khâu điều khiển số PI cứng hóa trên FPGA, tác 
giả tiến hành mô phỏng kết quả trên phần mềm 
ModelSim của Altera với chu kỳ CLOCK là 
0,1ms (trong thực tế hệ thống này cho phép mô 
phỏng lên đến 1ps), giá trị đặt r = 100 (số nguyên 
khi thực hiện trên chíp). Kết quả được chỉ ra trên 
Hình 10 (a-tổng thể, b là phóng lớn) cho thấy hệ 
Hình 9. Một phần cấu trúc hệ điều khiển sử dụng bộ PI số xây dựng trên nền tảng FPGA
thống ổn định xác lập ở thời gian 41ms với giá trị 
đầu ra xác lập y = 100 tương ứng giá trị đầu vào 
đặt r = 100. Nếu so sánh với việc mô phỏng trên 
Matlab thì số chu kỳ để đạt được giá trị xác lập 
ổn định thì ở đây đáp ứng nhanh hơn nhiều. Điều 
đó nhờ vào hoạt động độc lập của bộ điều khiển 
được thiết kế cứng, chúng không phụ thuộc vào 
các vòng quét của CPU.
Hình 10. Kết quả mô phỏng hệ thống khi xây dựng bộ điều khiển số trên FPGA
77
QUY NHON UNIVERSITY
SCIENCEJOURNAL OF
Journal of Science - Quy Nhon University, 2020, 14(1), 71-78
Như vậy, ta thấy thực hiện bộ điều khiển 
trên phần cứng và phần mềm đều cho kết quả 
của hệ thống ổn định và xác lập trạng thái đáp 
ứng đầu ra. Đồng thời tốc độ làm việc của bộ 
điều khiển PI số được xây dựng trên phần cứng 
(Hardware) phụ thuộc vào tốc độ Clock của 
FPGA mà không phụ thuộc vào chu kỳ vòng 
quét của CPU như trước đây. 
2.4. Xây dựng hệ thống thực nghiệm
Ưu điểm của FPGA trong việc thiết kế phần 
cứng một cách dễ dàng và khả năng tái cấu trúc 
phần cứng nhiều lần hay cho phép người dùng 
thay đổi cấu trúc bộ điều khiển ngay cả khi đang 
hoạt động. Trong nội dung mục này, tác giả thực 
hiện cấu hình thực nghiệm bộ điều khiển dòng 
điện (PI) trên nền tảng FPGA chíp Cyclone V 
5CSEMA5F31C6 của hãng Altera. Thực nghiệm 
này được thực hiện trên KIT De1SoC. Sau khi 
thiết kế bằng ngôn ngữ Verilog, ta tiến hành biên 
dịch để tạo file.sof chứa chuỗi Bitstream (nhị 
phân) cấu hình cho FPGA. Đối với KIT De1SoC 
cấu trúc 5CSEMA5F31C6 chia làm hai phần: 
một là lõi mềm ARM, hai là FPGA ở đây file.
sof chỉ cấu hình cho phần FPGA (phần bên phải 
của Hình 11).
Hình 11. Cấu hình phần cứng trên chíp Cyclone V 
5CSEMA5F31C6 - KIT De1SoC Altera
Sau khi cấu hình thành công trên phần 
cứng FPGA, hệ thống được chạy thực trên 
KITDe1Soc và đo đạt đầu ra trên oscilloscope 
thông qua các chân đáp ứng đầu ra “y”. Kết quả 
Hình 12 là quá trình tổng thể và thời điểm quá 
trình quá độ Hình 13. 
Hình 12. Kết quả thực nghiệm hệ thống điều khiển
Hình 13. Quá trình quá độ của thực nghiệm
Để dễ dàng biểu diễn trạng thái đáp ứng 
đầu ra, ta tiếp tục tiến hành thay đổi tần số hiển 
thị biểu diễn các kết quả thực nghiệm khi truy 
xuất các số liệu thực nghiệm từ file.xls trên 
oscilloscope điện tử và xây dựng biểu đồ như 
Hình 14.
Hình 14. Biểu diễn hệ thống đáp ứng đầu ra “y” và 
kích thích đầu vào từ các số liệu thực nghiệm
Một lần nữa, kết quả thực nghiệm cho thấy 
việc xây dựng bộ điều khiển dòng điện trên nền 
78
TRƯỜNG ĐẠI HỌC QUY NHƠN
KHOA HỌCTẠP CHÍ
Tạp chí Khoa học - Trường Đại học Quy Nhơn, 2020, 14(1), 71-78
tảng FPGA là hoàn toàn phù hợp hướng nghiên 
cứu trong tương lai và tiến đến ứng dụng trên các 
thiết bị điều khiển thương mại. 
3. KẾT LUẬN
Với nội dung thực hiện ở trên, bài báo đã đưa ra 
được các vấn đề sau đây: Đề xuất xây dựng bộ 
điều khiển dòng điện (cụ thể PI, hoặc PID) trên 
nền FPGA là hoàn toàn hợp lý. Việc xây dựng bộ 
điều khiển dòng điện trên phần cứng giúp giảm 
tải cho CPU và tăng khả năng đáp ứng, rút ngắn 
thời gian thực hiện điều khiển. 
Bằng kết quả mô phỏng trên phần mềm 
ModelSim và thực nghiệm trên KITDe1SoC cho 
kết quả đáp ứng tốt, thời gian xác lập nhanh, 
không phụ thuộc vào chu trình phần mềm.
TÀI LIỆU THAM KHẢO
1. W. Wang and P. Zhao. Application of kalman 
filter in the CNC servo control system, Symp. 
Secur. Detect. Inf. Process., 2010, 7, 442-446.
2. Y. C. Xiaohong Wang, Zhiffeng Pan, Thi Thu 
Giang Hoang, Liafang Tian. New Repetitive 
curent controller for PWM Rectifier, IFAC 
International Fed. Autom. Control., 2018, 154-
159.
3. E. R. Alphonsus and M. O. Abdullah. A review 
on the applications of programmable logic 
controllers (PLCs), Renew. Sustain. Energy Rev., 
2016, 60, 1185-1205.
4. P. Ponce, A. Molina, G. Tello, L. Ibarra, B. 
MacCleery, and M. Ramirez. Experimental 
study for FPGA pid position controller in CNC 
Micro-machines, IFAC Proc. Vol., 2015, 48(3), 
2203-2207.
5. M. Aboelaze and M. G. Shehata. Implementation 
of Multiple PID Controllers on, 978-1-5090-
0246-7/15/2015 IEEE, 2015, 446-449.
6. L. Kong, L. Zhu, L. Zhang, H. Bao, and C. 
Rao. Real-Time Controller Based on FPGA and 
DSP for Solar Ground Layer Adaptive Optics 
Prototype System at 1-m NVST, IEEE Photonics 
J., 2017, 9(2), 1-11.
7. B. D. Reddy, N. K. Anish, M. P. Selvan, and 
S. Moorthi. Embedded control of n-level DC-
DC-AC inverter, IEEE Trans. Power Electron., 
2015, 30(7), 3703-3711.
8. J. Karttunen, S. Kallio, J. Honkanen, P. 
Peltoniemi, and P. Silventoinen. Stability and 
performance of current harmonic controllers for 
multiphase PMSMs, Control Eng. Pract., 2017, 
65, 59-69.
9. M. R. Stanković, S. M. Manojlović, S. M. Simić, 
S. T. Mitrović, and M. B. Naumović. FPGA 
system-level based design of multi-axis ADRC 
controller, Mechatronics, 2016, 40, 146-155.
10. Q. Tang, L. Jiang, X. X. Liu, and Q. Dai. A real-
time updatable FPGA-based architecture for fast 
regular expression matching, Procedia Comput. 
Sci., 2014, 31(2014), 852-859. 
11. J. V. Frances-Villora, A. Rosado-Muñoz, J. 
M. Martínez-Villena, M. Bataller-Mompean, 
J. F. Guerrero, and M. Wegrzyn. Hardware 
implementation of real-time Extreme Learning 
Machine in FPGA: Analysis of precision, 
resource occupation and performance, Comput. 
Electr. Eng., 2016, 51, 139-156.
12. Y. Chen, B. Xie, and E. Mao. Electric Tractor 
Motor Drive Control Based on FPGA, IFAC-
PapersOnLine, 2016, 49(16), 271-276.
13. M. Curkovic, K. Jezernik, and R. Horvat. FPGA-
based predictive sliding mode controller of a 
three-phase inverter, IEEE Trans. Ind. Electron., 
2013, 60(2), 637-644.
14. J. Cigánek, M. Kocúr, and Š. Kozák. Hardware 
Realization of Advanced Controller Design 
Methods using FPGA, IFAC-PapersOnLine, 
2016, 49(5), 163-168.
15. M. Hanifzadegan and R. Nagamune. Contouring 
Control of CNC Machine Tools Based on Linear 
Parameter-Varying Controllers, IEEE/ASME 
Trans. Mechatronics, 2016, 21(5), 2522-2530.
16. Nguyen Phung Quang. Điều khiển tự động 
truyền động điện xoay chiều 3 pha, Nxb Giáo 
Dục, 1998.
17. V. B. Patel and R. H. Acharya. Design of FPGA-
based All Digital PID Controller for Dynamic 
Systems, Int. J. Adv. Res. Electr. Electron. 
Instrum. Eng. Vol. 1, Issue 2, 2012, 1(2), 64-72.
18. G. Zhao, Y. Zhao, A. Dong, and L. Zhang. 
Research on Nonlinear PID Position Controller 
of CNC System, 2007 IEEE Int. Conf. Autom. 
Logist., 2007, 2446-2450.