Control of two - wheeled inverted pendulum robot using robust pi and lqr controllers
In this paper, a robust PI controller in combination with a linear
quadratic regulator (LQR) is proposed to control a two-wheeled inverted pendulum
robot (TWIPR) such that it is kept balanced while moving. The proposed TWIPR
control system consists of two control loops. The inner loop has two PI controllers
for two DC motors’ currents, which are separately designed based on a robust PI
controller structure. The outer loop contains a LQR controller for the tilt angle,
heading angle and position of the TWIPR. The proposed PI controller is compared
to the existing method such as the magnitude optimum (MO) and genetic algorithm
(GA) methods. The proposed control scheme is verified through simulations and
practical tests, and it is also compared to the MO-LQR and GA-LQR strategies.

Trang 1

Trang 2

Trang 3

Trang 4
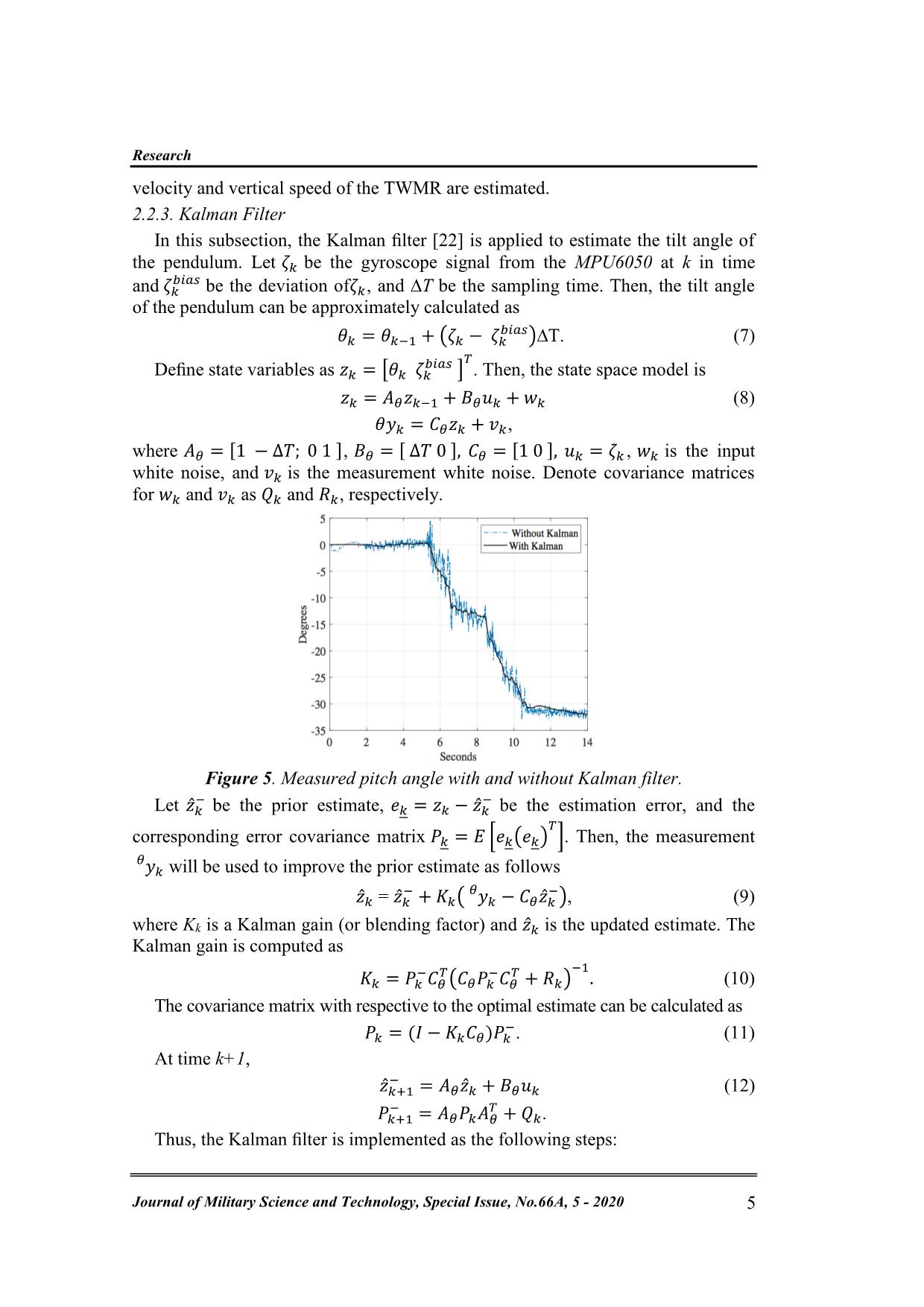
Trang 5

Trang 6
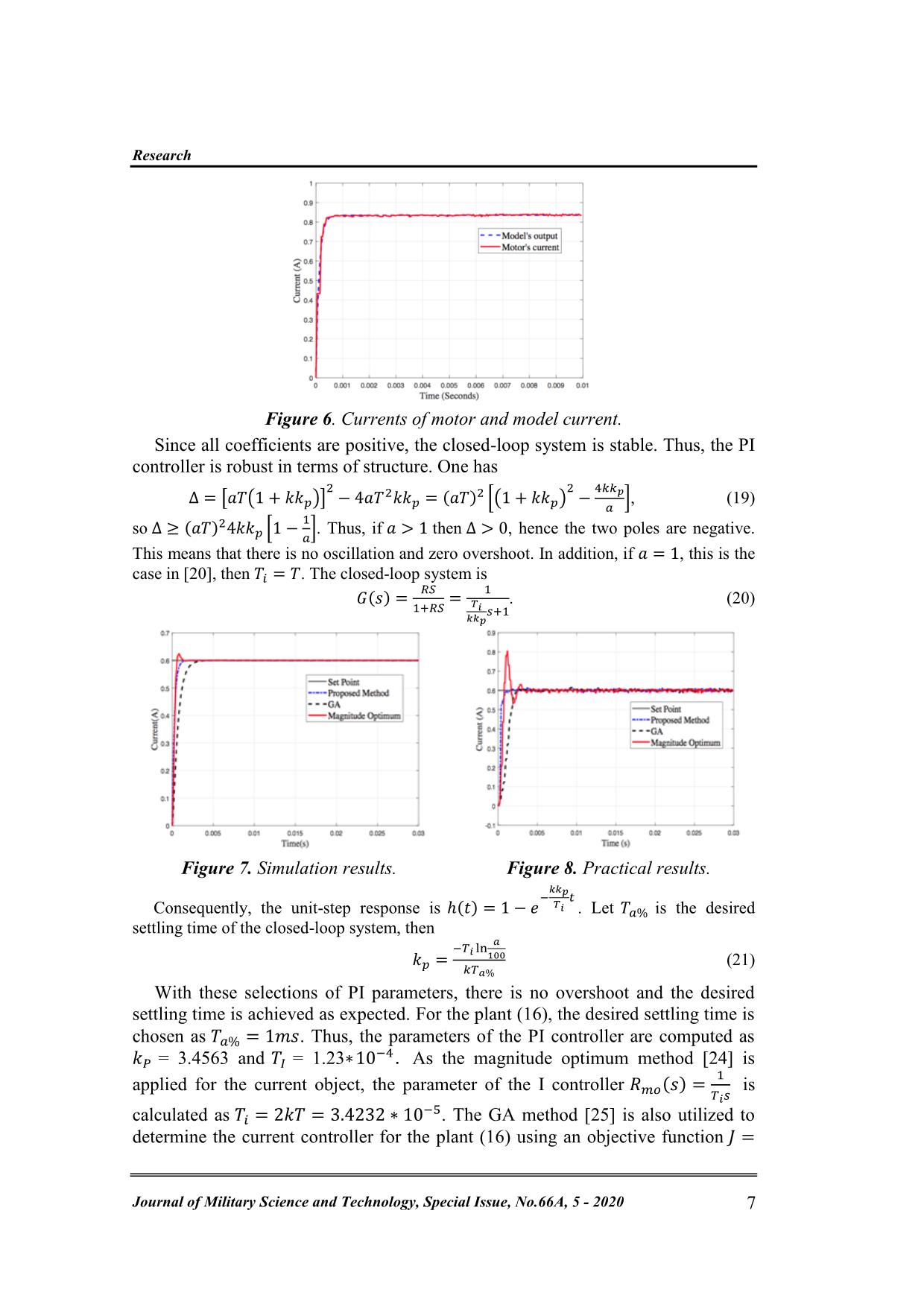
Trang 7
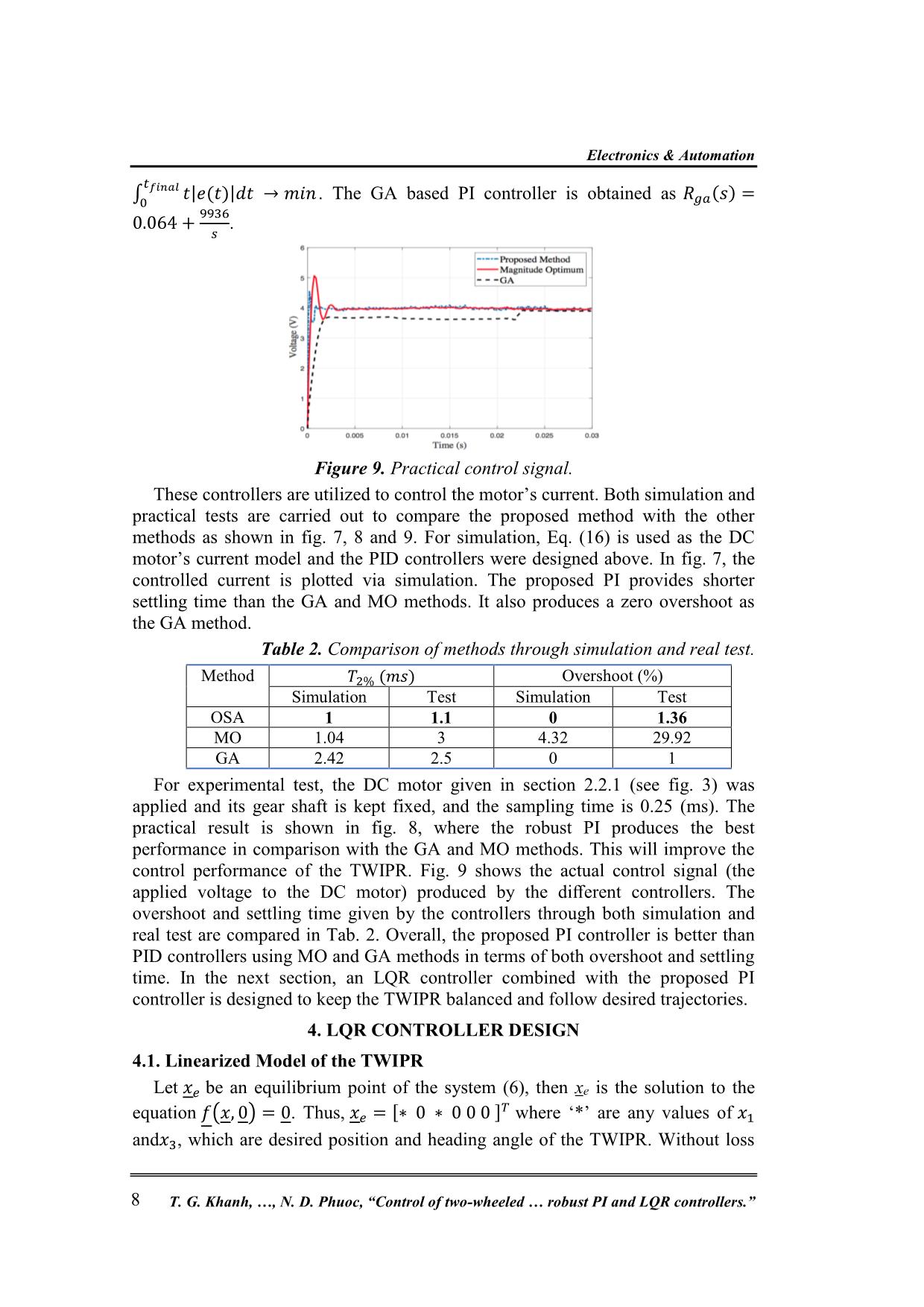
Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Control of two - wheeled inverted pendulum robot using robust pi and lqr controllers

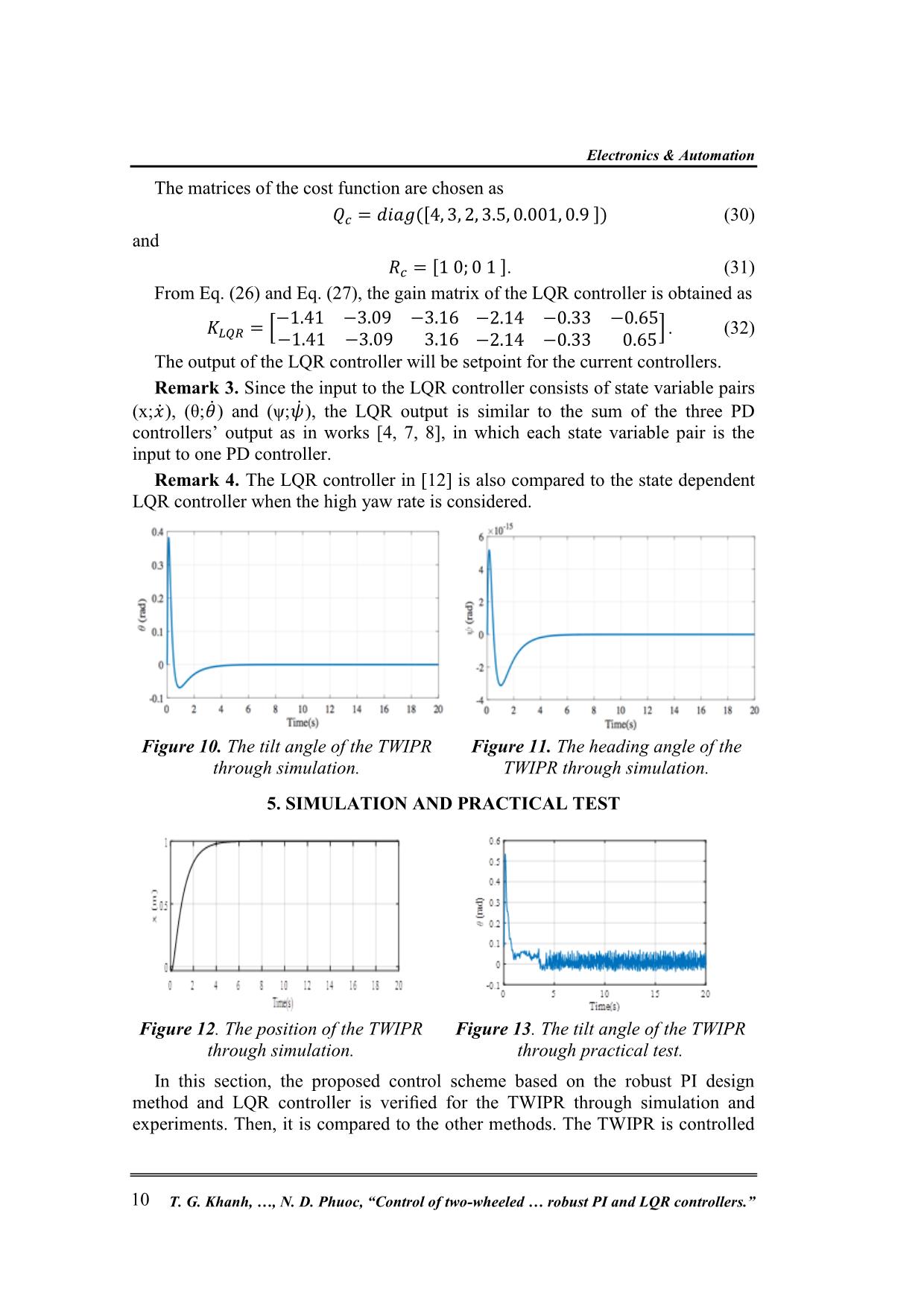
𝑏62], (24) with 𝑎42 = −(𝑀𝑔𝑙)2𝑔 𝛬 , 𝑎44 = −2𝐶((𝑀𝑙2+𝐼2)+𝑀𝑙𝑟) 𝛬 , 𝑎45 = 2𝐶𝑟(𝑀𝑙2+𝐼2)+2𝐶𝑀𝑙 2 𝛬 , 𝑎52 = 𝑀𝑔𝑙(2𝐽+𝑀𝑟2+2𝑚𝑟2) 𝛬 , 𝑎54 = 2𝐶𝑀𝑙+2𝐶(2𝐽+𝑀𝑟2+2𝑚𝑟2)/𝑟 𝛬 , 𝑎55 = 2𝐶(2𝐽+𝑀𝑟2+2𝑚𝑟3)+2𝐶𝑀𝑙𝑟 −𝛬 , 𝑎66 = −𝐶𝑑2 2𝐽𝑑2+(2𝐼3+4𝐾+𝑚𝑑2)𝑟2 , 𝑏41 = 𝑏42 = 𝐾𝑚𝑟[(𝑀𝑙 2+𝐼2)+𝑀𝑙𝑟] 𝛬 , 𝑏51 = 𝑏52 = −𝐾𝑚(2𝐽+𝑀𝑟 2+2𝑚𝑟2+𝑀𝑙𝑟) 𝛬 , 𝑏61 = −𝑏62 = −𝐾𝑚𝑑𝑟 𝐽𝑑2+(2𝐼3+4𝐾+𝑑2𝑚)𝑟2 , and 𝛬 = 2𝐼2𝐽 + 2𝐽𝑀𝑙2 + 𝐼2𝑀𝑟 2 + 2𝐼2𝑚𝑟 2 + 2𝑀𝑙2𝑚𝑟2. 4.2. LQR Controller From the linearized model (22), a LQR controller [26] is designed such that the following cost function is minimized. 𝐹 = ∫ (𝑥𝑇𝑄𝑐𝑥 + 𝑢 𝑇𝑅𝑐𝑢)𝑑𝑡 ∞ 0 → 𝑚𝑖𝑛, (25) in which 𝑄𝑐 is a symmetric positive definite matrix, and 𝑅𝑐 is a symmetric nonnegative definite matrix. The controller, which satisfies the cost function (25), is 𝑢 = −𝐾𝐿𝑄𝑅𝑥, where 𝐾𝐿𝑄𝑅 = 𝑅𝑐 −1𝐵𝑇𝑃𝑐, (26) and 𝑃𝑐 is the solution to the Riccati equation 𝑃𝑐𝐵𝑅𝑐 −1𝐵𝑇𝑃𝑐 − 𝑃𝑐𝐴 − 𝐴 𝑇𝑃𝑐 = 𝑄𝑐. (27) In this paper, the values of the TWIPR’s parameters are determined from a real TWIPR as follows M = 0.5kg, m = 0.04kg, l = 0.08m, d = 0.16m, r = 0.033m, g = 9.81m/s2, C = 0.005, Km = 0.41202Nm/A. Thus, the matrix B is 𝐵 = [0 0; 0 0; 0 0; 55.5 55.5; −548.6 − 548.6; −138.9 138.9 ], (28) and the matrix A has the form as in Eq. (29) with 𝑎42 = −11.4, 𝑎44 = −40.8, 𝑎45 = 1.35, 𝑎52 = 176.8, 𝑎54 = 403.4, 𝑎55 = −13.31, 𝑎66 = −8.1. 𝐴 = [ 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 𝑎42 0 𝑎44 𝑎45 0 0 𝑎52 0 𝑎54 𝑎55 0 0 0 0 0 0 𝑎66 ] (29) Electronics & Automation T. G. Khanh, , N. D. Phuoc, “Control of two-wheeled robust PI and LQR controllers.” 10 The matrices of the cost function are chosen as 𝑄𝑐 = 𝑑𝑖𝑎𝑔([4, 3, 2, 3.5, 0.001, 0.9 ]) (30) and 𝑅𝑐 = [1 0; 0 1 ]. (31) From Eq. (26) and Eq. (27), the gain matrix of the LQR controller is obtained as 𝐾𝐿𝑄𝑅 = [ −1.41 −3.09 −3.16 −2.14 −0.33 −0.65 −1.41 −3.09 3.16 −2.14 −0.33 0.65 ] . (32) The output of the LQR controller will be setpoint for the current controllers. Remark 3. Since the input to the LQR controller consists of state variable pairs (x;�̇�), (θ;�̇�) and (ψ;�̇�), the LQR output is similar to the sum of the three PD controllers’ output as in works [4, 7, 8], in which each state variable pair is the input to one PD controller. Remark 4. The LQR controller in [12] is also compared to the state dependent LQR controller when the high yaw rate is considered. Figure 10. The tilt angle of the TWIPR through simulation. Figure 11. The heading angle of the TWIPR through simulation. 5. SIMULATION AND PRACTICAL TEST Figure 12. The position of the TWIPR through simulation. Figure 13. The tilt angle of the TWIPR through practical test. In this section, the proposed control scheme based on the robust PI design method and LQR controller is verified for the TWIPR through simulation and experiments. Then, it is compared to the other methods. The TWIPR is controlled Research Journal of Military Science and Technology, Special Issue, No.66A, 5 - 2020 11 to move from the initial point to the end point along a line, where the distance between these two points is 1 meter. 5.1. The proposed control strategy The simulation results are shown in fig. 10, 11 and 12 whereas the experimental results are shown in fig. 13, 14 and 15. The left motor’s measured current and right motor’s measured current are shown in fig. 16 and 17. For simulation, the origin model as Eq. (6) and its parameters given in section 4.2 are applied for the TWIPR, in which the current control loops are modeled as saturation blocks since their settling time is very short 1 (ms). Figure 14. The real heading angle of the TWIPR. Figure 15. The real position of the TWIPR. For experimental test, the sampling time for PID and LQR controllers is chosen as 0.25 (ms) and 2.5 (ms), respectively. From fig. 10 to fig. 15, it can be implies that the real-time results are similar to the simulation results. This implies that a good model of the TWIPR was built and the controllers work well. The proposed control strategy produces good performance such as the pitch angle lies within the interval [−3 3] (degrees), the TWIPR reaches the destination at 1 (m) after 3.5 (seconds) following a straight line because the yaw angle is approximately within the range [−0.3 0.3] (degrees). 5.2. Comparisons The proposed control scheme based on the robust PI-LQR method is compared to the MO-LQR and GA-LQR methods through practical tests. The desired trajectory is a straight line with a length of 1 meter. Fig. 18 shows the positions of the TWIPR with different methods, where the blue curve, the black curve and the red curve are positions of the TWIPR provided by the proposed method, the MO- LQR method and the GA-LQR method, respectively. The comparison of the pitch and yaw angles of the TWIPR with different methods are shown in fig. 19 and fig. 20, respectively. Since the yaw angles are very small for all methods, the TWIPR moves nearly along the straight line with distance of 1 meter. The robust PI-LQR based TWIPR moves more smoothly from the start point 0 to the end point with smaller pitch angle and less oscillation than the other methods. Hence, the proposed controller provides better performance than the others. Electronics & Automation T. G. Khanh, , N. D. Phuoc, “Control of two-wheeled robust PI and LQR controllers.” 12 Figure 16. Left motor’s real current. Figure 17. Right motor’s real current. Figure 18. The position of the TWIPR with different methods. Figure 19. The pitch angle of the TWIPR with different methods. Figure 20. The yaw angle of the TWIPR with different methods. Remark 5: The proposed control scheme is also tested with different loads and inclined surfaces. The practical results prove that the TWIPR is kept balanced and movable. However, they are skipped to show here. 6. CONCLUSIONS In this work, the TWIPR control system based on the robust PI controller design method is proposed. First, the proposed method is compared to the MO and GA Research Journal of Military Science and Technology, Special Issue, No.66A, 5 - 2020 13 methods through the DC motor’s current. It produces better performance than the others. Then, the proposed control system is verified and compared to the other methods through simulations and practical tests. The obtained results show that the TWIPR with the proposed method is kept balanced and able to reach the desired position and direction, and it produces better performance than the others. Future works will focus on the combination of the proposed method with other advanced control methods for the TWIPR. ACKNOWLEDGEMENT This research is funded by the Hanoi University of Science and Technology (HUST) under project number T2018-PC-052. REFERENCES [1]. A. L. Cullen, "A new free-wave method for ferrite measurements at millimeter wavelengths," Radio Science, Vol. 22, pp. 1168-1170, (1987). [2]. L. Zhijun, Y. Chenguang, and F. Liping, “Advanced Control of Wheeled Inverted Pendulum Systems,” Springer, 280, (2013). [3]. P. M. C. Ronald, A. S. Karl, and H. Roger, “Review of modeling and control of two-wheeled robots,” Annual Reviews in Control, Vol. 37, pp. 89-103, (2013). [4]. T. G. Khanh, N. D. Phuoc, and N. H. Nam, “Advanced control methods for two-wheeled mobile robots,” The proceedings of the International Conference on System Science and Engineering. Ho Chi Minh, Vietnam, (2017). [5]. N. N. Son and P. H. H. Anh, “Adaptive Back-stepping Self-balancing Control of a Two-wheel Electric Scooter,” Int. Jour. Advan. Robo. Syst., Vol. 11, pp. 1–11, (2014). [6]. D. Fuquan, G. Xueshan, J. Shigong, G. Wenzeng, and L. Yubai, “A two- wheeled inverted pendulum robot with friction compensation,” Mechatronics Vol. 30, pp. 116–125. (2015). [7]. R. M. Brisilla and V. Sankaranarayanan, “Nonlinear control of mobile inverted pendulum,” Robotics and Autonomous Systems, Vol. 70, pp. 145– 155, (2015). [8]. T. C. Sung and J. Seul, “Combining Two Control Techniques for the Fast Movement of a Two-Wheel Mobile Robot,” Int. J. Human. Robot, Vol. 12, pp. 1–14, (2015). [9]. H. W. Kim and S. Jung, “Control of a two-wheel robotic 300 vehicle for personal transportation,” Robotica, Vol. 34, pp. 1186– 1208, (2016). [10]. O. Akos, B. Ervin, K. Istvan, F. Janos and O. A. Peter, Fuzzy Control of a Two-Wheeled Mobile Pendulum System,” Proceedings of the 11th IEEE Int. Symp. Appl. Comp. Intel. and Infor., Romania, (2016). [11]. Y. Ming, A. Cong, D. Yu and S. Jianzhong, “Indirect adaptive fuzzy control for a nonholonomic/underactuated wheeled inverted pendulum vehicle based on a data-driven trajectory planner,” Fuzzy Sets and Systems, Vol. 290, pp. 158–177, (2016). [12]. Y. Ming, W. Shuang and S. Jian-Zhong, “Simultaneous balancing and trajectory tracking control for two-wheeled inverted pendulum vehicles: A Electronics & Automation T. G. Khanh, , N. D. Phuoc, “Control of two-wheeled robust PI and LQR controllers.” 14 composite control approach,” Neurocomputing Vol. 191, pp.44–54, (2016). [13]. K. Sangtae and K. SangJoo, “Nonlinear Optimal Con315 trol Design for Underactuated Two-Wheeled Inverted Pendulum Mobile Platform,” IEEE/ASME Transactions on Mechatronics, Vol. 22, pp. 2803 – 2808, (2017). [14]. N. Esmaeili, A. Alireza and K. Hossein, “Balancing and Trajectory Tracking of Two-Wheeled Mobile Robot Using Backstepping Sliding Mode Control: Design and Experiments,” Journal of Intelligent and Robotic Systems, Vol. 83, pp. 601–613, (2017). [15]. H. Jian, H. R. Myong, W. Dongrui and R. Songhyok, “Interval Type-2 Fuzzy Logic Modeling and Control of a Mobile Two-Wheeled Inverted Pendulum,” IEEE Transactions on Fuzzy Systems, Vol. 26, pp. 2030–2038, (2018). [16]. L. Rongjun, W. Junfeng, W. Dan, “Sampled-data Fuzzy Control of Two- wheel Inverted Pendulums Based on Passivity Theory,” International Journal of Control, Automation and Systems, Vol. 16, pp. 2538-2548, (2018). [17]. J. Seonghee and H. Taisei, “Development of a wheeled inverted pendulum mobile platform with a four-bar parallel mechanism,” Advanced Robotics, Vol. 32, pp. 1–11, (2018). [18]. Y. Ming, A. Cong and S. Jian-Zhong, “An Efficient Model Predictive Control for Trajectory Tracking of Wheeled Inverted Pendulum Vehicles with Various Physical Constraints,” International Journal of Control, Automation and Systems, Vol. 16, pp. 265–274, (2018). [19]. N. Yigao, Y. Ming, Y. Lu and H. Xiaoqiang, “A trajectory planning and tracking control approach for obstacle avoidance 340 of wheeled inverted pendulum vehicles,” International Journal of Control, https://doi.org/10.1080/00207179.2018.1530455 (2018). [20]. H. Chunsheng, H. Kang, C. Xiaolong, Z. Yiran and Z. Han “Transportation control of cooperative double-wheel inverted pendulum robots adopting Udwadia- control approach,” Nonlinear Dynamics, Vol. 91, pp. 2789–2802, (2018). [21]. N. H. Nam and N. D. Phuoc, “Overshoot and settling time assignment with pid for first order and second-order systems,” IET Control Theory and Applications, Vol. 12, pp. 2407– 2416, (2018). [22]. K. Sangtae and K. SangJoo, “Dynamic Modeling of a Two-wheeled Inverted Pendulum Balancing Mobile Robot,” International Journal of Control, Automation, and Systems, Vol. 13, pp. 926–933, (2015). [23]. G. B. Robert and Y. C. H. Patrick, “Introduction to Random Signals and Applied Kalman Filtering with Matlab Exercises,” Fourth Edition, John Wiley and Sons, Inc, (2012). [24]. P. Jinzhu and D. Rickey, “Identification and adaptive neural network control of a DC motor system with dead-zone characteristics,” ISA Transactions, Vol. 50, pp. 588–598, (2011). [25]. W. U. Jeffrey and S. Mohammed, “Magnitude and symmetric optimum criterion for the design of linear control systems: What is it and how does it compare with the others?,” IEEE Trans. Indus. Appl., Vol. 26, pp. 489–497, (1990). [26]. T. Neenu and P. Poongodi, “Position Control of DC Motor Using Genetic Algorithm Based PID Controller,” Proc. Worl. Cong. Engineering, London Research Journal of Military Science and Technology, Special Issue, No.66A, 5 - 2020 15 UK, pp. 1–5, (2009). [27]. D. O. A. Brian and B. M. John, “Optimal Control: Linear Quadratic Methods,” Prentice-Hall International, Inc, (1989). [28]. T. G. Khánh, L. V. Anh, P. A. Tuấn, P. X. Minh, N. H. Nam, “Điều khiển xe hai bánh tự cân bằng mô hình bất định dựa trên phương pháp quy hoạch động thích nghi,” The 1st National Conference on Dynamics and Control, Danang, Vietnam, (2019). [29]. N. V. Khanh, T. T. Hùng, “Điều khiển thời gian thực robot hai bánh tự cân bằng sử dụng bộ điều khiển PID mờ tự chỉnh,” Hội nghị toàn quốc lần thứ 3 về Điều khiển và Tự động hoá, (2015). [30]. N. M. Tâm, N. V. Đ. Hải, N. P. Lưu, L. V. Tuấn, “Mô hình hóa và điều khiển tối ưu cho hệ xe hai bánh tự cân bằng,” Đại học Sư phạm Kỹ thuật Hồ Chí Minh, (2017). [31]. A. N. K. Nasir, M. A. Ahmad, R. M. T. Raja Ismail, "The Control of a Highly Nonlinear Two-wheels Balancing Robot: A Comparative Assessment between LQR and PID-PID Control Schemes," WASET International Journal of Mechanical and Mechatronics Engineering, Vol. 4, (2010). [32]. A. Y. Zimit, H. J. Yap, M. F. Hamza, I. Siradjuddin, B. Hendrik, T. Herawan, "Modeling and Experimental Analysis Two-Wheeled Self Balance Robot Using PID Controller," Lecture Notes in Computer Science, Vol. 10961, Springer, Cham, (2018). TÓM TẮT ĐIỀU KHIỂN XE HAI BÁNH CÂN BẰNG SỬ DỤNG BỘ ĐIỀU KHIỂN PI BỀN VỮNG VÀ LQR Trong bài báo này, một bộ điều khiển PI bền vững kết hợp với bộ điều khiển LQR được đề xuất được đề xuất để điều khiển xe hai bánh sao cho xe thằng bằng khi di chuyển. Hệ thống điều khiển gồm hai vòng. Vòng trong có hai bộ điều khiển dòng PI để điều khiển dòng động cơ một chiều, được thiết kế riêng sử dụng cấu trúc PI bền vững. Vòng ngoài có bộ điều khiển LQR cho góc nghiêng, góc hướng và vị trí xe. Phương pháp thiết kế bộ điều khiển PI đề xuất được so sánh với phương pháp tối ưu độ lớn và giải thuật di truyền. Cấu trúc điều khiển đề xuất được kiểm chứng thông qua mô phỏng và thực nghiệm, và nó được so sánh với các phương pháp MO-LQR và GC-LQR. Từ khóa: Chỉnh định PID; Xe hai bánh; Điều khiển động cơ; Thời gian xác lập. Received date, 02nd March 2020 Revised date, 14th April 2020 Published 06th May, 2020 Author affiliations: 1Hanoi University of Science and Technology, No. 1, Dai Co Viet Street, Hanoi, Vietnam; 2Viện Hàng không Vũ trụ Viettel; 3Công ty Ô tô Toyota Việt Nam. *Corresponding author: nam.nguyenhoai@hust.edu.vn.
File đính kèm:
 control_of_two_wheeled_inverted_pendulum_robot_using_robust.pdf
control_of_two_wheeled_inverted_pendulum_robot_using_robust.pdf

