Chinh phục kỳ thi THPT Quốc gia - Ứng dụng tích phân
Câu 10: (Mã đề 101 - BGD - 2019) Cho hàm số f x liên tục trên . Gọi S là diện tích hình
phẳng giới hạn bởi các đường y f x y x , 0, 1 và x 4 (như hình vẽ bên). Mệnh đề
nào dưới đây đúng?
Câu 11: (Mã đề 104 - BGD - 2019) Cho hàm số f x liên tục trên . Gọi S là diện tích hình phẳng
giới hạn bởi cá đường y f x , y x 0, 2 và x 3 (như hình vẽ). Mệnh đề nào dưới
đây đúng?

Trang 1

Trang 2

Trang 3
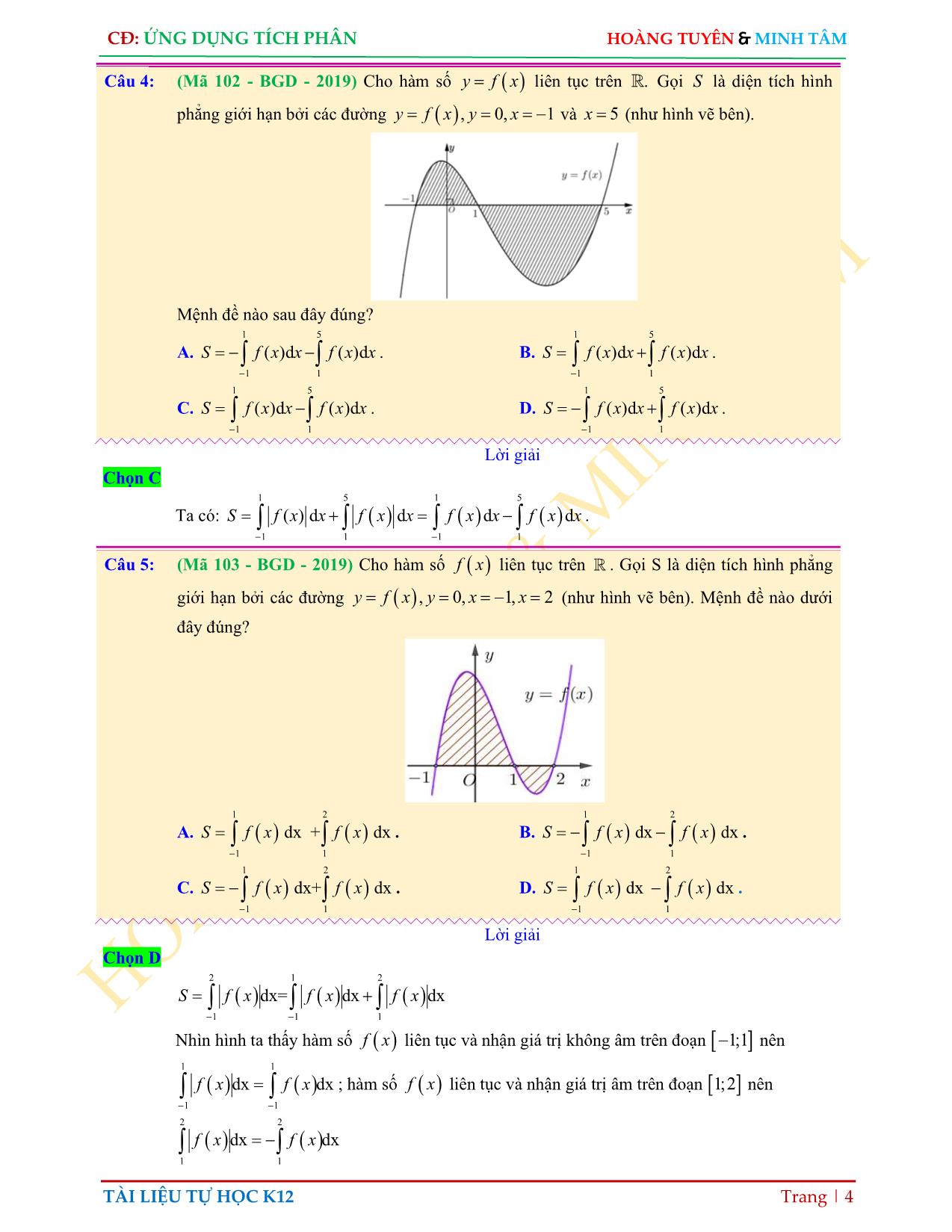
Trang 4
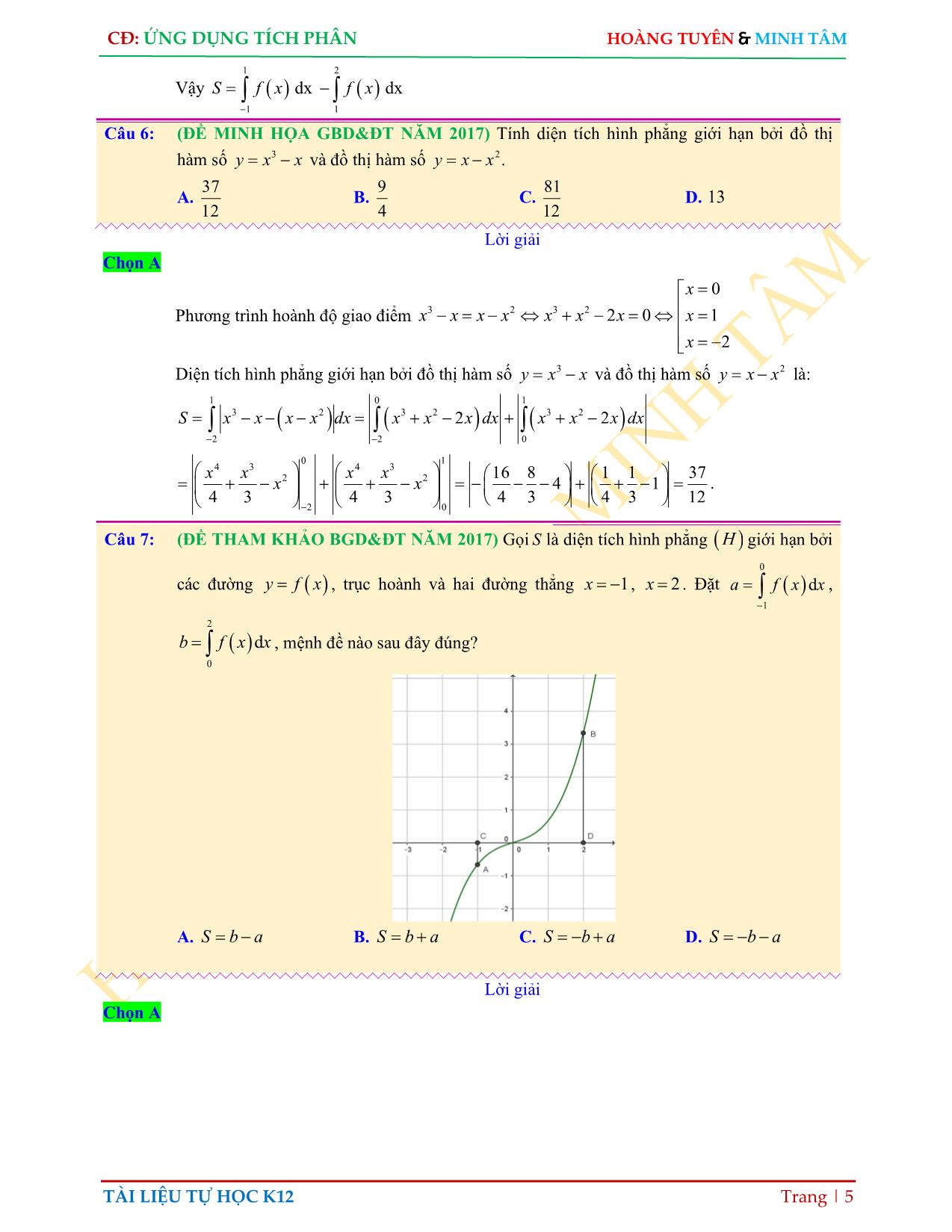
Trang 5
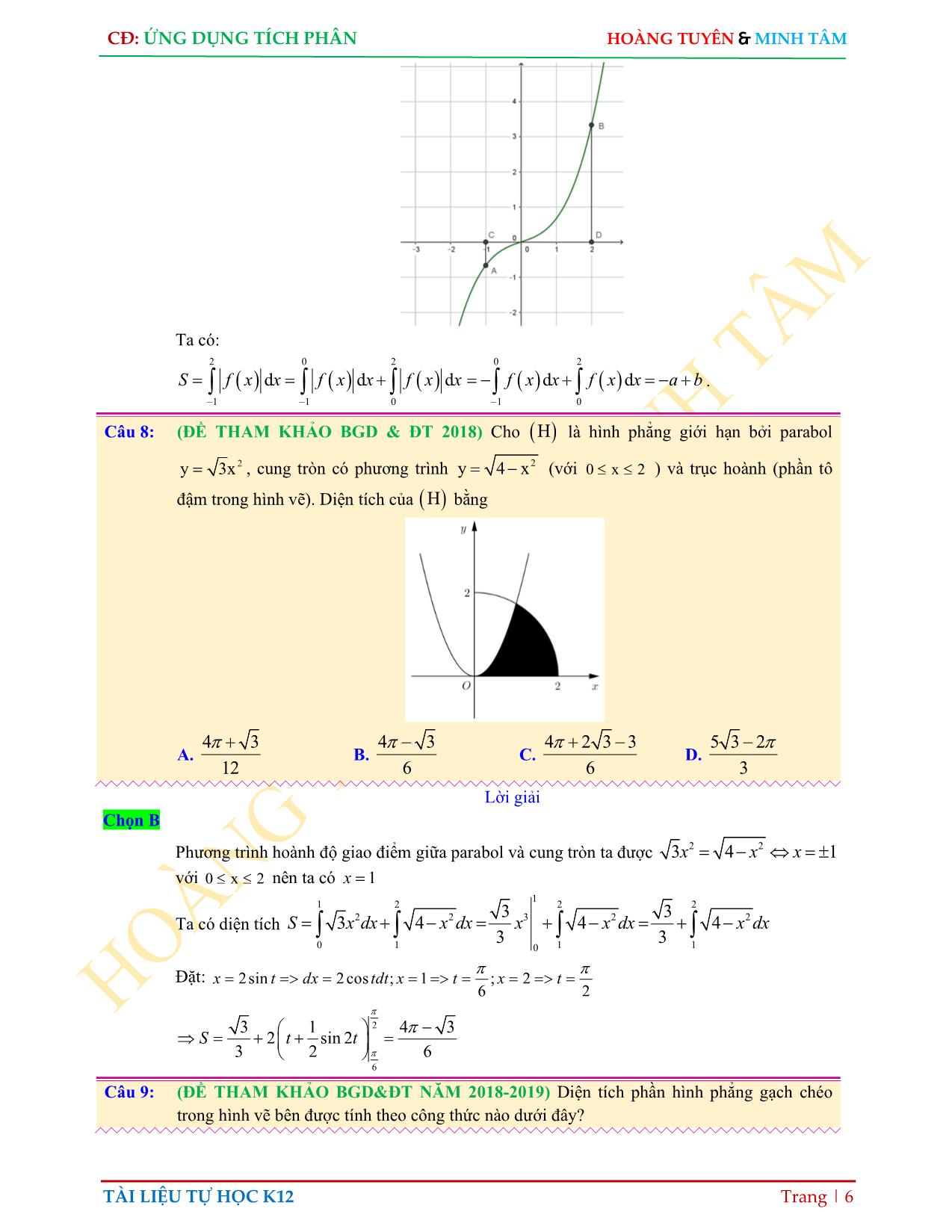
Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Chinh phục kỳ thi THPT Quốc gia - Ứng dụng tích phân", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Chinh phục kỳ thi THPT Quốc gia - Ứng dụng tích phân

MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 108 Ta có 2 2 2 2 0. tan 30 3 R xNM y R x NP MN . MNP có diện tích 2 21 1. . 2 2 3 R xS x NM NP . Thể tích hình nêm là 2 2 1 1d d 2 3 R R R R R xV S x x x 3 2 31 1 2 3 3 92 3 R R RR x x . * Chú ý: Có thể ghi nhớ công thức tính thể tích hình nêm: 2 3 1 2 2 tan 3 3 V R h R , trong đó 2 ABR , PMN . Câu 183: (THPT LÊ QUÝ ĐÔN ĐÀ NẴNG NĂM 2018-2019) Cho một mô hình 3 D mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài 5 cm ; khi cắt hình này bởi mặt phẳng vuông góc với đấy của nó, ta được thiết diện là một hình parabol có độ dài đáy gấp đôi chiều cao parabol. Chiều cao của mỗi thiết diện parobol cho bởi công thức 23 5 y x cm , với x cm là khoảng cách tính từ lối vào lớn hơn của đường hầm mô hình. Tính thể tích (theo đơn vị 3cm ) không gian bên trong đường hầm mô hình ( làm tròn kết quả đến hàng đơn vị ) A. 29 . B. 27 . C. 31. D. 33 . Lời giải Chọn A Xét một thiết diện parabol có chiều cao là h và độ dài đáy 2h và chọn hệ trục Oxy như hình vẽ trên. Parabol P có phương trình 2: , 0P y ax h a Có ;0B h P 20 ah h 1 0a dohh Diện tích S của thiết diện: 2 21 4dx 3 h h hS x h h , 23 5 h x 2 4 23 3 5 S x x Suy ra thể tích không gian bên trong của đường hầm mô hình: CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 109 25 5 0 0 4 2dx 3 dx 28,888 3 5 V S x x 329 cmV Câu 184: (TT THANH TƯỜNG NGHỆ AN NĂM 2018-2019 LẦN 02) Một chi tiết máy được thiết kế như hình vẽ bên. Các tứ giác ,ABCD CDPQ là các hình vuông cạnh 2,5cm . Tứ giác ABEF là hình chữ nhật có 3,5BE cm . Mặt bên PQEF được mài nhẵn theo đường parabol P có đỉnh parabol nằm trên cạnh EF . Thể tích của chi tiết máy bằng A. 3395 24 cm . B. 350 3 cm . C. 3125 8 cm . D. 3425 24 cm . Lời giải Chọn D Gọi hình chiếu của ,P Q trên AF và BE là R và S . Vật thể được chia thành hình lập phương .ABCD PQRS có cạnh 2,5cm , thể tích 31 125 8 V cm và phần còn lại có thể tích 2V . Khi đó thể tích vật thể 1 2 2 125 8 V V V V . Đặt hệ trục Oxyz sao cho O trùng với F , Ox trùng với FA , Oy trùng với tia Fy song song với AD . Khi đó Parabol P có phương trình dạng 2y ax , đi qua điểm 51; 2 P do đó 25 5 2 2 a y x . Cắt vật thể bởi mặt phẳng vuông góc với Ox và đi qua điểm ,0 1;0;0M x x ta được thiết diện là hình chữ nhật MNHK có cạnh là 25 2 MN x và 5 2 MK do đó diện tích 225 4 S x x CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 110 Áp dụng công thức thể tích vật thể ta có 1 2 2 0 25 25 4 12 V x dx Từ đó 3125 25 425 8 12 24 V cm Câu 185: (THPT LỤC NGẠN - LẦN 1 - 2018) Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn 28cm , trục nhỏ 25cm . Biết cứ 31000cm dưa hấu sẽ làm được cốc sinh tố giá 20000 đồng. Hỏi từ quả dưa hấu trên có thể thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể. A. 183000 đồng. B. 180000 đồng. C. 185000 đồng. D. 190000 đồng. Lời giải Chọn A Đường elip có trục lớn 28cm , trục nhỏ 25cm có phương trình 2 2 125 2 y 2 2 2 2 25 1 2 14 xy 2 2 25 1 2 14 xy . Do đó thể tích quả dưa là 2 14 2 2 14 25 1 2 14 xV x d 22 14 2 2 14 25 1 2 14 dx x 142 3 2 14 25 . 2 3.14 xx 225 56. 2 3 8750 3 3cm . Do đó tiền bán nước thu được là 8750 .20000 183259 3.1000 đồng. Câu 186: (THPT THỰC HÀNH - TPHCM - 2018) Một cốc rượu có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc (bổ dọc cốc thành 2 phần bằng nhau) là một đường Parabol. Tính thể tích tối đa mà cốc có thể chứa được (làm tròn 2 chữ số thập phân) A. 3320V cm . B. 31005,31V cm . C. 3251,33V cm . D. 3502,65V cm . Lời giải Chọn C CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 111 Parabol có phương trình 2 25 8 8 5 y x x y Thể tích tối đa cốc: 10 0 8 . 251,33 5 V y dy . Câu 187: (THPT CHUYÊN THOẠI NGỌC HẦU - LẦN 3 - 2018) Có một cốc nước thủy tinh hình trụ, bán kính trong lòng đáy cốc là 6cm , chiều cao lòng cốc là 10cm đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết khi nghiêng cốc nước vừa lúc khi nước chạm miệng cốc thì đáy mực nước trùng với đường kính đáy. A. 3240 cm . B. 3240 cm . C. 3120cm . D. 3120 cm . Lời giải Chọn A Cách 1. Xét thiết diện cắt cốc thủy tinh vuông góc với đường kính tại vị trí bất kỳ có: 2 2 2 21 . . tan 2 S x R x R x 2 21 tan2S x R x . CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 112 Thể tích hình cái nêm là: 2 2 31 2tan d tan2 3 R R V R x x R . Thể tích khối nước tạo thành khi nguyên cốc có hình dạng cái nêm nên 32 tan 3kn V R . 3 32 . 240cm 3kn hV R R . Cách 2. Dựng hệ trục tọa độ Oxyz Gọi S x là diện tích thiết diện do mặt phẳng có phương vuông góc với trục Ox với khối nước, mặt phẳng này cắt trục Ox tại điểm có hoành độ 0 h x . Gọi , , IOJ FHN OE x 6tan 10 IJ EF OJ OE 6 10 xEF 66 10 xHF . 66 10cos 1 6 10 x HF x HN ; arccos 1 10 x 2 1 1.2 . .sin 2 2 2 HMNhinhquatS x S S HN HM HN 2 2 16 arccos 1 .6.6.2 1 1 1 10 2 10 10 x x xS x 210 10 0 0 d 36arccos 1 36 1 1 1 d 240 10 10 10 x x xV S x x x . Câu 188: (THPT CHUYÊN THOẠI NGỌC HẦU - LẦN 3 - 2018) Cho vật thể đáy là hình tròn có bán kính bằng 1 (tham khảo hình vẽ). Khi cắt vật thể bằng mặt phẳng vuông góc với trục Ox tại điểm có hoành độ 1 1x x thì được thiết diện là một tam giác đều. Thể tích V của vật thể đó là O xE J H M N F I x S x 10cm 12cm CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 113 A. 3V . B. 3 3V . C. 4 3 3 V . D. V . Lời giải Chọn C Do vật thể có đáy là đường tròn và khi cắt bởi mặt phẳng vuông góc với trục Ox được thiết diện là tam giác đều do đó vật thể đối xứng qua mặt phẳng vuông góc với trục Oy tại điểm O . Cạnh của tam giác đều thiết diện là: 22 1a x . Diện tích tam giác thiết diện là: 2 23 1 3 4 aS x . Thể tích khối cần tìm là: 11 1 3 2 0 0 0 4 32 2 3 1 2 3 3 3 xV Sdx x x . Câu 189: (THPT BÌNH GIANG - HẢI DƯƠNG - 2018) Sân vận động Sport Hub (Singapore) là sân có mái vòm kỳ vĩ nhất thế giới. Đây là nơi diễn ra lễ khai mạc Đại hội thể thao Đông Nam Á được tổ chức tại Singapore năm 2015 . Nền sân là một elip E có trục lớn dài 150m , trục bé dài 90m (hình 3). Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của E và cắt elip ở ,M N (hình 3) thì ta được thiết diện luôn là một phần của hình tròn có tâm I (phần tô đậm trong hình 4) với MN là một dây cung và góc 090 .MIN Để lắp máy điều hòa không khí thì các kỹ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vật liệu là mái không đáng kể. Hỏi thể tích xấp xỉ bao nhiêu? 1-x2 O x CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 114 Hình 3 A. 357793m . B. 3115586m . C. 332162m . D. 3101793m . Lời giải Chọn B Chọn hệ trục như hình vẽ Ta cần tìm diện tích của S x thiết diện. Gọi ,d O MN x 2 2 2 2: 1.75 45 x yE Lúc đó 2 2 2 2 22 2 45 1 90 175 75 x xMN y 2 2 2 2 2 2 90 90. 1 . 1 75 2 752 2 MN x xR R CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 115 2 2 2 2 2 1 1 1 1 20252 . 1 . 4 2 4 2 2 75 xS x R R R Thể tích khoảng không cần tìm là 75 2 3 2 75 20252 . 1 115586 . 2 75 xV m Câu 190: (TRẦN PHÚ - HÀ TĨNH - LẦN 2 - 2018) Một cái thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có trục lớn bằng 1m , trục bé bằng 0,8m , chiều dài (mặt trong của thùng) bằng 3m . Đươc đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ đáy thùng đến mặt dầu) là 0,6m . Tính thể tích V của dầu có trong thùng (Kết quả làm tròn đến phần trăm). A. 31,52mV . B. 31,31mV . C. 31,27mV . D. 31,19mV . Lời giải Chọn A Chọn hệ trục tọa độ như hình vẽ. Theo đề bài ta có phương trình của Elip là 2 2 11 4 4 25 x y . Gọi M , N lần lượt là giao điểm của dầu với elip. Gọi 1S là diện tích của Elip ta có 1 1 2. 2 5 5 S ab . Gọi 2S là diện tích của hình phẳng giới hạn bởi Elip và đường thẳng MN . Theo đề bài chiều cao của dầu hiện có trong thùng (tính từ đáy thùng đến mặt dầu) là 0,6m nên ta có phương trình của đường thẳng MN là 1 5 y . Mặt khác từ phương trình 2 2 11 4 4 25 x y ta có 24 1 5 4 y x . Do đường thẳng 1 5 y cắt Elip tại hai điểm M , N có hoành độ lần lượt là 3 4 và 3 4 nên CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 116 3 3 4 4 2 2 2 3 3 4 4 4 1 1 4 1 3d d 5 4 5 5 4 10 S x x x x . Tính 3 4 2 3 4 1 d 4 I x x . Đặt 1 1sin d cos d 2 2 x t x t t . Đổi cận: Khi 3 4 x thì 3 t ; Khi 3 4 x thì 3 t . 3 3 2 3 3 1 1 1 1 2 3. cos d 1 cos 2 d 2 2 8 8 3 2 I t t t t . Vậy 2 4 1 2 3 3 3 5 8 3 2 10 15 20 S . Thể tích của dầu trong thùng là 3 .3 1,52 5 15 20 V . CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 117 DẠNG TOÁN 5: ỨNG DỤNG CỦA TÍCH PHÂN ĐỂ GIẢI MỘT SỐ BÀI TOÁN ĐẠI SỐ Câu 191: (PTNK CƠ SỞ 2 - TPHCM - LẦN 1 - 2018) Cho hàm số y f x có đạo hàm f x liên tục trên đoạn 0;5 và đồ thị hàm số y f x trên đoạn 0;5 được cho như hình bên. Tìm mệnh đề đúng A. 0 5 3f f f . B. 3 0 5f f f . C. 3 0 5f f f . D. 3 5 0f f f . Lời giải Chọn C Ta có 5 3 5 3 0f x x f f d , do đó 5 3f f . 3 0 3 0 0f x x f f d , do đó 3 0f f 5 0 5 0 0f x x f f d , do đó 5 0f f Câu 192: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số y f x . Đồ thị của hàm số y f x như hình bên. Đặt 22 1g x f x x . Mệnh đề nào dưới đây đúng? A. 1 3 3g g g B. 1 3 3g g g C. 3 3 1g g g D. 3 3 1g g g BÀI TẬP NỀN TẢNG & VẬN DỤNG CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 118 Lời giải Chọn B Ta có 2 2 1g x f x x 10 1 3 x g x f x x x . Bảng biến thiên Suy ra 3 1g g và 3 1g g . (1) Gọi 1S là diện tích hình phẳng giới hạn bởi các đường: '( ), 1, 3, 1y f x y x x x Gọi 2S là diện tích hình phẳng giới hạn bởi các đường: 1, '( ), 1, 3y x y f x x x Dựa vào hình vẽ, ta thấy: 1 2 0S S . Suy ra: 1 2 0S S 1 3 3 1 1 d 1 d 0f x x x x f x x 1 3 3 1 1 d 1 d 0f x x x f x x x 3 3 1 d 0f x x x . Khi đó: 3 3 3 3 3 3 d 2 1 d 0g g g x x f x x x (2) Từ (1) và (2) suy ra: 1 3 3g g g . Câu 193: (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số ( )y f x . Đồ thị ( )y f x của hàm số như hình bên. Đặt 22g x f x x . Mệnh đề nào dưới đây đúng? CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 119 A. 3 3 1g g g B. 1 3 3g g g C. 3 3 1g g g D. 1 3 3g g g Lời giải Chọn D Ta có 2 2 0 3;1; 3g x f x x g x x . Từ đồ thị của y f x ta có bảng biến thiên của hàm g x . Suy ra 3 1g g . Kết hợp với BBT ta có: 1 3 3 3 3 1 1 1 d d d dg x x g x x g x x g x x 3 1 3 1 3 3g g g g g g Vậy ta có 3 3 1g g g . Câu 194: (MÃ ĐỀ 123 BGD&DT NĂM 2017) Cho hàm số y f x . Đồ thị hàm số 'y f x như hình vẽ. Đặt 22 .h x f x x Mệnh đề nào dưới đây đúng? A. 4 2 2h h h B. 2 2 4h h h C. 4 2 2h h h D. 2 4 2h h h Lời giải Chọn D CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 120 Ta có ' 2 ' ; ' 0 2; 2; 4 .h x f x x h x x Bảng biến thiên Suy ra 2 4h h . Kết hợp với đồ thị hàm số y=x ta có 4 2 d 0 4 2 0 4 2 .h x x h h h h Vậy ta có 2 4 2h h h . Câu 195: Cho hàm số y f x liên tục trên và có đồ thị của hàm số f x như hình bên dưới. Mệnh đề nào sau đây đúng? A. 0 2 1f f f . B. 0 1 2f f f . C. 2 0 1f f f . D. 1 0 2f f f . Lời giải Chọn B Theo đồ thị, ta có: 0 1 0 1 d 0f f f x x 0 1f f 1 , 2 0 2 1 1 0 2 1 d d d 0f f f x x f x x f x x 1 2f f 2 . CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 121 Từ 1 và 2 0 1 2f f f . Câu 196: (SỞ GD&ĐT PHÚ THỌ NĂM 2018-2019 LẦN 01) Cho hàm số .f x Đồ thị của hàm số y f x trên 3;2 như hình vẽ (phần cong của đồ thị là một phần của parabol 2 . y ax bx c ) Biết 3 0, f giá trị của 1 1 f f bằng A. 23 6 B. 31 6 C. 35 3 D. 9 2 Lời giải Chọn B Parabol 2 y ax bx c có đỉnh 2;1 I và đi qua điểm 3;0 nên ta có 2 2 12 4 2 1 4 4 3. 9 3 0 3 b aa a b c b y x x a b c c Do 3 0 f nên 1 1 1 0 0 1 2 1 3 f f f f f f f f 1 0 1 2 0 1 3 ( )d ( )d 2 4 3 d f x x f x x x x x 1 2 1 2 3 3 8 312 4 3 d 1 . 2 3 6 S S x x x Với 1 2,S S lần lượt là diện tích hình phẳng giới hạn bởi đồ thị hàm số , y f x trục Ox và hai đường thẳng 1, 0 x x và 0, 1. x x Dễ thấy 1 2 31; . 2 S S Câu 197: (THPT LƯƠNG VĂN CAN - LẦN 1 - 2018) Cho hàm số y f x . Đồ thị của hàm số y f x như hình vẽ. Đặt 22 1g x f x x . CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 122 Mệnh đề nào dưới đây đúng? A. 1 3 5g g g . B. 1 5 3g g g . C. 5 1 3g g g . D. 3 5 1g g g . Lời giải Chọn B Ta có 2 1g x f x x ; 0g x 1f x x . Dựa vào đồ thị ta có các nghiệm sau: 1 3 5 x x x . Ta có bảng biến thiên Ngoài ra dựa vào đồ thị ta có 3 5 1 3 1 1d d 2 2 g x x g x x 3 51 3g x g x 3 1 3 5g g g g 5 1g g . Vậy 3 5 1g g g . Câu 198: (THPT HẬU LỘC 2 - TH - 2018) Cho hàm số 3 2( ) , , , , 0y f x ax bx cx d a b c d a có đồ thị là C . Biết rằng đồ thị C đi qua gốc tọa độ và đồ thị hàm số '( )y f x cho bởi hình vẽ bên. CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 123 Tính giá trị (4) (2)H f f ? A. 45H . B. 64H . C. 51H . D. 58H . Lời giải Chọn D Theo bài ra 3 2( ) , , , , 0y f x ax bx cx d a b c d a do đó y f x là hàm bậc hai có dạng 2y f x a x b x c . Dựa vào đồ thị ta có: 1 4 4 c a b c a b c 3 0 1 a b c 23 1y f x x . Gọi S là diện tích phần hình phẳng giới hạn bởi các đường y f x , trục Ox , 4,x 2x . Ta có 4 2 2 3 1 dx 58S x . Lại có: 44 2 2 dx 4 2S f x f x f f . Do đó: 4 2 58H f f . Câu 199: (SGD THANH HÓA - LẦN 1 - 2018) Cho hàm số y f x . Đồ thị của hàm số y f x như hình vẽ bên. Đặt 2;6 maxM f x , 2;6minm f x , T M m . Mệnh đề nào dưới đây đúng? A. 0 2T f f . B. 5 2T f f . C. 5 6T f f . D. 0 2T f f . Lời giải Chọn B CĐ: ỨNG DỤNG TÍCH PHÂN HOÀNG TUYÊN 🙲 MINH TÂM TÀI LIỆU TỰ HỌC K12 Trang | 124 Gọi 1S , 2S , 3S , 4S lần lượt là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x với và trục hoành. Quan sát hình vẽ, ta có 0 2 2 0 d df x x f x x 0 02 2f x f x 0 2 0 2f f f f 2 2f f 2 5 0 2 d df x x f x x 0 52 2f x f x 0 2 5 2f f f f 0 5f f 5 6 2 5 d df x x f x x 5 52 6f x f x 5 2 5 6f f f f 2 6f f Ta có bảng biến thiên Dựa vào bảng biến thiên ta có 2;6 max 5M f x f và 2;6 min 2m f x f Khi đó 5 2T f f .
File đính kèm:
 chinh_phuc_ky_thi_thpt_quoc_gia_ung_dung_tich_phan.pdf
chinh_phuc_ky_thi_thpt_quoc_gia_ung_dung_tich_phan.pdf

