Chinh phục kỳ thi THPT Quốc gia môn Toán - Chuyên đề: Vận dụng cao môn Toán (Hình học)
LÝ THUYẾT:
Công thức tính thể tích khối chóp: S Bh 1
. Trong đó: B là diện tích đa giác đáy
h là đường cao của hình chóp
Diện tích xung quanh: Sxq tổng diện tích các mặt bên.
Diện tích toàn phần: S S tp xq diện tích đáy.
Các khối chóp đặc biệt:
Khối tứ diện đều: tất cả các cạnh bên đều bằng nhau
Tất cả các mặt đều là các tam giác đều
Khối chóp tứ giác đều: tất cả các cạnh bên đều bằng nhau
Đáy là hình vuông tâm O, SO vuông góc với đáy

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

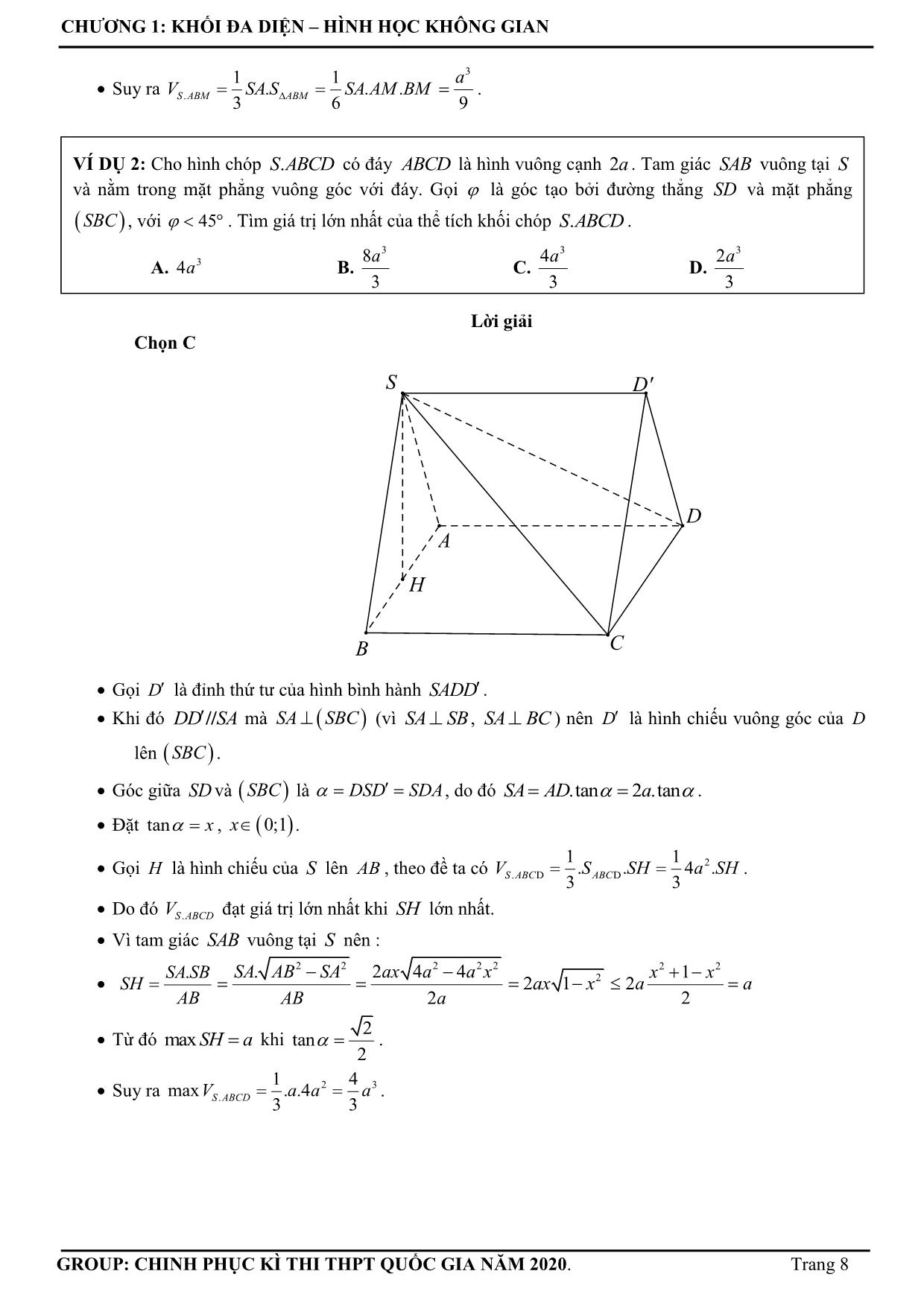
Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Chinh phục kỳ thi THPT Quốc gia môn Toán - Chuyên đề: Vận dụng cao môn Toán (Hình học)", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Chinh phục kỳ thi THPT Quốc gia môn Toán - Chuyên đề: Vận dụng cao môn Toán (Hình học)

3AB ku với 3 4; 1;6u . 3 4 3 2 4 0 1 2 0 6 2 6 1 v u k v AB ku v u k u v u k k . Đường thẳng 4d đi qua 3; 1;2A và có vtcp là 3 4; 1;6u nên 4 3 1 2 : 4 1 6 x y z d . CÂU 9: Chọn C * Gọi N d N nên 1 2 ; 1 ;N t t t . Khi đó ta có 2 1; 2;MN t t t . Đường thẳng có vectơ chỉ phương 2;1; 1a . * Vì . 0d MN a 2 2 1 2 2 0 3 t t t t 1 4 2 ; ; 3 3 3 MN . Chọn vectơ chỉ phương của d là 1; 4; 2da . * Vậy phương trình của 2 1 : 1 4 2 x y z d . CÂU 10: Chọn D Giả sử 2d d M 2 ; 1 ;1M t t t . 1 ; ; 2AM t t t . 1d có VTCP 1 1;4; 2u . 1 1. 0 1 4 2 2 0 5 5 0 1d d AM u t t t t t 2; 1; 1AM . Đường thẳng d đi qua 1; 1;3A có VTCP 2; 1; 1AM có phương trình là: 1 1 3 : . 2 1 1 x y z d . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 287 CHƯƠNG 3: HÌNH HỌC OXYZ CÂU 11: Chọn B Gọi đường thẳng cần tìm là , A là giao của và d . Khi đó: 2 3 ; 3 2 ;1A t t t , 3 3 ; 4 2 ; 1MA t t t . Do vuông góc với d nên: 2. 0MAu 7 7 0 1t t . Khi đó 6; 2;0MA , hay vectơ chỉ phương của là 3; 1;0 . Vậy phương trình : 1 3 1 2 x t y t z . CÂU 12: Chọn D Mặt phẳng có một véctơ pháp tuyến là 1;1; 1n . Gọi M là giao điểm của d và , ta có: 3 ;3 3 ;2M t t t suy ra 2;3 1;2 1AM t t t Do song song với mặt phẳng ( ) nên . 0n AM 2 3 1 2 1 0t t t 1t Khi đó 1; 2; 1AM là một véctơ chỉ phương của CÂU 13. Chọn C Gọi M d M d 3 ; 3 3 ; 2M t t t 2 ;1 3 ;1 2AM t t t . có VTPT là 1;1; 1n . // AM . 0AM n 2 1 3 1 2 0t t t 1t 1; 2; 1AM . Vậy 1 2 1 : 1 2 1 x y z . CÂU 14. Chọn B Gọi N d khi đó ta có MN là một véc tơ chỉ phương của đường thẳng . Do N d nên 2 2 ;2 ;3N t t t . Mà N nên 2 2 2 3 3 0t t t 1t 0;1;2N 1; 1;2MN . Vậy một vec tơ chỉ phương của là 1;1; 2u . CÂU 15: Chọn C Phương trình tham số của 1 : 2 x t d y t z t . Xét phương trình 2 1 2 2 1 0 1t t t t . Vậy đường thẳng d cắt mặt phẳng P tại 2; 1;3M . Gọi 1; 1;1da và 2; 1; 2n lần lượt là vectơ chỉ phương của d và vectơ pháp tuyến của mặt phẳng P . Khi đó một vectơ chỉ phương của đường thẳng cần tìm là , 3;4;1da a n . Vậy phương trình đường thẳng cần tìm là: 2 1 3 3 4 1 x y z . CÂU 16: Chọn B Gọi d là đường thẳng cần tìm Gọi 1 2,A d d B d d 1 22 ;1 ; 2 ; 1 2 ;1 ;3 2 2 1; ; 5A d A a a a B d B b b AB a b a b a GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 288 CHƯƠNG 3: HÌNH HỌC OXYZ P có vectơ pháp tuyến 7;1; 4Pn , pd P AB n cùng phương có một số k thỏa pAB kn 2 2 1 7 2 2 7 1 1 0 2 5 4 4 5 1 a b k a b k a a b k a b k b a k a k k d đi qua điểm 2;0; 1A và có vectơ chỉ phương 7;1 4d Pa n Vậy phương trình của d là 2 1 7 1 4 x y z . CÂU 17: Chọn D Với 2 1; 1; 1A t t t d và 3 ; 2 ; 1B t t t d , ta có A , B , M thẳng hàng khi. 2 1 2 2 2 0 2 1 2 2 2 2 22 2 t k t t k kt MA kMB t k t t k kt t k ktt k t hệ vô nghiệm. Vậy không có đường thẳng nào thỏa yêu cầu đề. CÂU 18: Chọn B Đường thẳng d có một VTCP là 1;1;2u Gọi 1 ; ; 1 2d M t t t ; ; 3 2AM t t t . Ta có d . 0AM u 2 3 2 0t t t 1t 1;1; 1AM Đường thẳng đi qua 1;0;2A , một VTCP là 1;1; 1AM có phương trình là 1 2 : 1 1 1 x y z . CÂU 19 : Đường thẳng d có một véc tơ chỉ phương là 1; 1; 2u . Gọi B d . Ta có B d nên 1 ; ; 1 2B t t t và ; ; 2 3AB t t t là một véc tơ chỉ phương của đường thẳng . Mặt khác d nên . 0AB u 6 6 0t 1t . Suy ra 1; 1; 1AB . Vậy phương trình chính tắc của đường thẳng là 1 2 1 1 1 x y z . CÂU 20: Chọn A Gọi A d A d P Tọa độ A thỏa mãn hệ 11 2 1 1;1;12 1 3 2 4 0 1 xx y z y A x y z z . Do P và d nên nhận ; 5; 1; 3P du n u là một véctơ chỉ phương. Đường thẳng đi qua 1;1;1A nên có dạng 1 1 1 5 1 3 x y z . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 289 CHƯƠNG 3: HÌNH HỌC OXYZ CÂU 21: Chọn A Giả sử P là mặt phẳng qua gốc tọa độ O và vuông góc với . Xét hình chiếu vuông góc của M trên P là điểm K ta có MK MH nên minMH khi và chỉ khi H K và khi đó đường thẳng d đi qua hai điểm ,O K sẽ là hình chiếu vuông góc của MO trên mặt phẳng P . Do vậy: , , , ,d P P du n n OM u u u OM . CÂU 22: Chọn A B thuộc tia Oz 0;0;B b , với 0b . 3OA , OB b . 6 2 6 6 b OB OA b b l . 0;0;6B , 1; 2; 4BA . Đường thẳng đi qua 0;0;6B và có VTCP 1; 2; 4BA có phương trình là: 6 : 1 2 4 x y z . CÂU 23: Chọn D Gọi là đường thẳng cần tìm, Pn là VTPT của mặt phẳng P . Gọi 1 ; ;2 2M t t t là giao điểm của và d ; 3 ;1 ;1 2M t t t là giao điểm của và d Ta có: 2 ; 1 ; 1 2 2MM t t t t t t //MM P P M P MM n 2t 4 ; 1 ; 3 2MM t t t Ta có cos30 cos , dMM u 2 3 6 9 2 36 108 156 t t t 4 1 t t Vậy, có 2 đường thẳng thoả mãn là 1 5 : 4 10 x y t z t ; 2 : 1 x t y z t GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 290 CHƯƠNG 3: HÌNH HỌC OXYZ Khi đó 1 2 1 cos , 2 . CÂU 24: Chọn D * Ta có: 3; 2;2PP n , 4;5; 1QQ n . * Do P Q AB P AB n AB Q AB n nên đường thẳng AB có véctơ chỉ phương là: ; 8; 11; 23Q Pu n n * Do AB cũng là một véc tơ chỉ phương của AB nên // 8; 11; 23AB u . CÂU 25: Chọn D Ta có véc – tơ chỉ phương của đường thẳng là 1;1;2u . Véc – tơ pháp tuyến của mặt phẳng : 2 1 0x y z là 1;1; 2n . Vì là mặt phẳng chứa đường thẳng có phương trình 2 1 1 1 2 x y z và vuông góc với mặt phẳng : 2 1 0x y z nên có một véc – tơ pháp tuyến là , 4;4;0 4 1; 1;0 4.n u n a . Gọi d , suy ra d có véc – tơ chỉ phương là , 2;2;2 2 1;1;1du a n . Giao điểm của đường thẳng có phương trình 2 1 1 1 2 x y z và mặt phẳng : 2 1 0x y z là 3;2;2I . Suy ra phương trình đường thẳng 3 : 2 2 x t d y t z t . Vậy 2;1;1A thuộc đường thẳng d . CÂU 26: Chọn B Đường thẳng d cần tìm là giao của P với Q là mặt phẳng trung trực của MN . Gọi I là trung điểm của MN 2;3;4I 2;2;2MN PTTQ của Q là – 2 – 3 – 4 0x y z hay : – 9 0Q x y z Phương trình đường thẳng d cần tìm là giao của P và Q PTTS của d là 9 0 2 3 14 0 x y z x y z hay 13 2 4 x t y t z t . CÂU 27: Chọn A Măt phẳng Oyz có phương trình 0x Gọi A là giao điểm của d và mặt phẳng Oyz suy ra 0; 7; 5A . Chọn 2; 3;1M d GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 291 CHƯƠNG 3: HÌNH HỌC OXYZ Gọi H là hình chiếu của M lên Oyz suy ra 0; 3;1H Hình chiếu vuông góc của d lên mặt phẳng Oyz là đường thẳng d đi qua H nhận 0; 4; 6 2 0; 2;3AH có phương trình: 0 : 3 2 1 3 x d y t z t . CÂU 28: Chọn B Giao điểm của d và mặt phẳng Oxz là: 0 (5;0;5)M . Trên 1 2 : 2 4 3 x t d y t z t chọn M bất kỳ không trùng với 0 (5;0;5)M ; ví dụ: (1; 2;3)M . Gọi A là hình chiếu song song của M lên mặt phẳng Oxz theo phương 1 6 2 : 1 1 1 x y z . +/ Lập phương trình d’ đi qua M và song song hoặc trùng với 1 6 2 : 1 1 1 x y z . +/ Điểm A chính là giao điểm của d’ và Oxz +/ Ta tìm được (3;0;1)A Hình chiếu song song của 1 2 : 2 4 3 x t d y t z t lên mặt phẳng Oxz theo phương 1 6 2 : 1 1 1 x y z là đường thẳng đi qua 0 (5;0;5)M và (3;0;1)A . Vậy phương trình là 3 0 1 2 x t y z t . CÂU 29. Chọn D Giả sử 22 2 2 2 22 2 2 22 2 1; ; 1 ; ; 1; 1; 1 1 1; ; 1 1 1 AM x y zAM x y z M x y z BM x y z BM x y z CM x y z CM x y z 2 2 22 2 2 2 2 23 2 3 1 2 1 1MA MB MC x y z x y z 2 221 1x y z 2 2 22 2 2 3 5 54 4 4 6 4 8 6 2 2 1 2 2 2 4 4 x y z x y z x y z . Dấu " " xảy ra 3 4 x , 1 2 y , 1z , khi đó 3 1 ; ; 1 4 2 M . CÂU 30: Chọn A Ta có ; ;d A d d B d OA OB . Dấu " " xảy ra OA d OB d d có VTCP là ; 7;7;7 7 1;1;1u OA OB . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 292 CHƯƠNG 3: HÌNH HỌC OXYZ Vậy : 1 1 1 x y z d . CÂU 31: Chọn D Gọi 1 ; 2 ;2M t t t 2 2MA MB 2 2 2 2 2 2 6 2 2 2 4 4 2t t t t t t 212 48 76t t Ta có: 2212 48 76 12 2 28 28t t t Vậy 2 2MA MB nhỏ nhất bằng 28 khi 2t hay 1;0;4M . CÂU 32 Chọn B Phương trình tham số của đường thẳng : 1 1 x t d y t z t . Do ;1 ;1M d M t t t . Khi đó 21 ; ; 1 3 2MA t t t MA t và 21 ; 1 ; 3 2MB t t t MB t . Do vậy 22 3 2 2 2T MA MB t . Suy ta min 2 2T khi 0 0;1;1t M . CÂU 33: Chọn A Mặt cầu S có tâm 0;1;1I và bán kính 3 R . Gọi H là hình chiếu của I trên P và A là giao điểm của IH với S . Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng P đến một điểm thuộc mặt cầu S là đoạn AH . 3 3 , 2 AH d I P R . CÂU 34: Chọn B Ta có: 3 2.0 2.1 5 . 1 2. 1 2.3 5 24 0 . A , B là hai điểm nằm khác phía so với mặt phẳng P . Gọi H là hình chiếu của B lên . Ta có: BH BA nên khoảng cách từ B đến lớn nhất khi và chỉ khi H trùng A . Khi đó: AB . Mặt phẳng P có vectơ pháp tuyến là 1; 2;2 n . 4; 1;2 AB . 1 , n n AB 2;6;7 . Đường thẳng đi qua điểm 3;0;1 A và nhận 1 2;6;7 n làm vectơ chỉ phương. GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 293 CHƯƠNG 3: HÌNH HỌC OXYZ Phương trình đường thẳng là: 1 12 13 2 6 7 x y z . CÂU 35: Chọn B Gọi 12 ;2 ; 1 2P t t t d và 2 4 ;2 3 ;2Q t t t . Ta có: 1;1; 2a , 4; 3; 1b và 4 ; 3 ; 2 3PQ t t t t t t . Khi đó: 4 3 2 2 3 0. 0 4 4 3 3 1 2 3 0. 0 t t t t t ta PQ t t t t t tb PQ . 3 6 6 0 26 3 3 1 t t t t t t . Suy ra 1;1;1P và 2;2;2Q 1;1;1PQ . Nên 1 : 1 1 x t d y t z t . Gọi 1 ;1 ;1M t t t nên 3; 3;NM t t t . Do đó: 2 2 22 23 3 3 12 18 3 2 6 6NM t t t t t t . Đoạn thẳng MN ngắn nhất bằng 6 khi 2t . Suy ra 3;3;3 9M a b c . CÂU 36: Chọn A 1S có tâm 1 3; 2; 2I , bán kính 1 2R . 2S có tâm 2 1; 0; 1I , bán kính 2 1R . Ta có: 1 2 1 23I I R R , do đó 1S và 2S tiếp xúc ngoài với nhau tại điểm 5 2 4 ; ; 3 3 3 A . Vì d tiếp xúc với hai mặt cầu, đồng thời cắt đoạn thẳng nối hai tâm 1 2I I nên d phải tiếp xúc với hai mặt cầu tại A 1 2d I I . Mặt khác ;d d O d OA maxd OA khi d OA . Khi đó, d có một vectơ chỉ phương là 1 2 , 6; 3; 6I I OA 2; 1; 2u . Suy ra 2a , 2b . Vậy 2S . CÂU 37: Chọn B GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 294 CHƯƠNG 3: HÌNH HỌC OXYZ Ta có 3 6AB ; 2 6AC ; 6BC . Ta có 1 2 3 1 2 2 3 32 3 2T d d d d d d d d . Gọi M là trung điểm AB , và N là trung điểm của BC ta có 1 22 ;d M d d và 2 32 ;d N d d . Gọi G là trọng tâm tam giác MNC . Khi đó ta có 32 ; 2 ; 2 6 ;T d M d N d d G . Do đó 6 ; 6 ;T d G d G d . Ta có 5 3 1; ; 2 2 M ; 7 5 3; ; 2 2 N suy ra 2;3; 2G . Gọi 1 ;1 2 ;1H t t t là hình chiếu của G lên đường thẳng d , ta có 1; 2 2;3GH t t t . . 0 1 2 2 2 3 0 0dGH u t t t t . Vậy 2 2 2 max 6 6 1 2 3 6 14T GH . CÂU 38: Chọn A Gọi 1 1 2 ;2 ; 2M d M t t t d có vectơ chỉ phương 2 2; 2; 1da AM t t t 2 có vectơ chỉ phương 2 1;2;2a 2 2 2 2 cos ; 3 6 14 9 t d t t Xét hàm số 2 26 14 9 t f t t t , ta suy ra được min 0 0 0f t f t Do đó min cos , 0 0 2;2 1d t AM Vậy phương trình đường thẳng d là 1 1 2 2 1 x y z . CÂU 39: Chọn B 1 2 1 2 ; ; 2 1 ; 2 3 ;2 2 A d A a a a B d B b b b có vectơ chỉ phương 2 ;3 2; 2 4AB b a b a b a P có vectơ pháp tuyến 1;1;1Pn Vì / / P nên . 0 1P PAB n AB n b a .Khi đó 1;2 5;6AB a a a GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 295 CHƯƠNG 3: HÌNH HỌC OXYZ 2 2 2 2 2 1 2 5 6 6 30 62 5 49 7 2 6 ; 2 2 2 AB a a a a a a a Dấu " " xảy ra khi 5 5 9 7 7 6; ; , ;0; 2 2 2 2 2 a A AB Đường thẳng đi qua điểm 5 9 6; ; 2 2 A và vec tơ chỉ phương 1;0;1du Vậy phương trình của là 6 5 2 9 2 x t y z t . CÂU 40: Chọn A Mặt cầu S có tâm 2;3;5I , bán kính 10R . Do (I, ( )) Rd nên luôn cắt S tại A , B . Khi đó 22 (I, )AB R d . Do đó, AB lớn nhất thì ,d I nhỏ nhất nên qua H , với H là hình chiếu vuông góc của I lên . Phương trình x 2 2t y 3 5 : 2 z t B tH ( ) 2 2 2 2 3 – 2 5 15 0H t t t 2; 7;t 2 3H . Do vậy AH (1;4;6) là véc tơ chỉ phương của . Phương trình của 3 3 3 1 4 6 x y z . CÂU 41: Chọn A d d (Q) (P) A I A K H Đường thẳng d đi qua 1; 1; 3M và có véc tơ chỉ phương 1 2; 1; 1u . Nhận xét rằng, A d và 7; 3; 1d P I . Gọi Q là mặt phẳng chứa d và song song với . Khi đó , , ,d d d Q d A Q . Gọi H , K lần lượt là hình chiếu vuông góc của A lên Q và d . Ta có AH AK . Do đó, ,d d lớn nhất ,d A Q lớn nhất maxAH H K . Suy ra AH chính là đoạn vuông góc chung của d và . Mặt phẳng R chứa A và d có véc tơ pháp tuyến là 1,Rn AM u 2; 4; 8 . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 296 CHƯƠNG 3: HÌNH HỌC OXYZ Mặt phẳng Q chứa d và vuông góc với R nên có véc tơ pháp tuyến là 1,Q Rn n u 12; 18; 6 . Đường thẳng chứa trong mặt phẳng P và song song với mặt phẳng Q nên có véc tơ chỉ phương là ,P Ru n n 66; 42; 6 6 11; 7; 1 . Suy ra, 11; 7a b . Vậy 2 3a b . CÂU 42: Chọn A Phương trình tham số của : 1 2 2 3 x t d y t z t . ; 1 2 ; 2 3M d M t t t . 22 2 2 1 2 2 2 3 3 , 2 2 1 2 2 t t t d M P 5 2 3 t 5 6 5 6 t t 11 1 t t . Vì M có hoành độ âm nên chọn 1t . Khi đó tung độ của M bằng 3 . CÂU 43: Chọn C Gọi mặt phẳng đi qua M nhận 1; 2; 1AM làm vectơ pháp tuyến nên: : 1 1 2 2 1 3 0R x y z 2 8 0x y z . Gọi d là giao tuyến của mặt phẳng R và P . Vectơ pháp tuyến của mp P là: 1; 1; 2n Ta có , 5; 3; 1u AM n Gọi M là điểm thuộc giao tuyến của R và P nên tọa độ M là nghiệm của hệ 2 8 0 2 1 0 0 x y z x y z x 0 3 2 x y z nên 0; 3; 2M Phương trình đường thẳng d : 0 5 3 3 2 x t y t z t Ta có B d nên 5 ; 3 3 ; 2B t t t Mặt khác M là trung điểm của đoạn BC nên 2.1 5 2.2 3 3t z 2.3 2 C C C x t y t 2 5 1 3t z 4 C C C x t y t Mặt khác C Q nên 2 5 2 1 3 4 4 0t t t 10 0t 0t . Nên 2;1;4C nên 7T a b c . CÂU 44 : Chọn D Ta có 1 . ; . 2 MABS d M AB AB nên MAB có diện tích nhỏ nhất khi ;d M AB nhỏ nhất. Gọi là đường vuông góc chung của ,d AB . Khi đó M d . Gọi N AB . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 297 CHƯƠNG 3: HÌNH HỌC OXYZ Ta có: 1;2;0AB , phương trình đường thẳng : 1 2 2 x s AB y s z Do N AB ; 1 2 ;2N s s , M d 1 ; ;1M t t t . 1; 2 1; 1NM t s t s t . Mà ,MN d MN nên 4 1 2 4 2 0 3 5 1 3 1 2 1 1 0 3 3 1 1 t s t s t s t t s t s t t s s . Do đó 1 4 7 ; ; 3 3 3 M hay 2 3 10T a b c . CÂU 45: Chọn A Cách 1 : Ta có 2;1;2AB ; 2;2;1AC Do , 3; 6;6AB AC nên 1 9 , 2 2 ABCS AB AC . Gọi n là một véc tơ pháp tuyến của mặt phẳng ABC thì 1;2; 2n phương trình mặt phẳng ABC là 2 2 2 0x y z . Gọi 1 2 ; 2 ;3 2M t t t d 4 11 , 3 t d M ABC . Do thể tích V của tứ diện MABC bằng 3 nên 4 111 9 . . 3 3 2 3 t 4 11 6t 5 4 17 4 t t . Với 5 4 t thì 3 3 1 ; ; 2 4 2 M .Với 17 4 t thì 15 9 11 ; ; 2 4 2 M . Cách 2: Ta có 2;1;2AB ; 2;2;1AC , 3; 6;6AB AC Gọi 1 2 ; 2 ;3 2M t t t d 1 2 ; 3 ;3 2AM t t t . Vì 1 , . 6 MABCV AB AC AM nên 12 33 18t 5 4 17 4 t t Với 5 4 t thì 3 3 1 ; ; 2 4 2 M .Với 17 4 t thì 15 9 11 ; ; 2 4 2 M . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 298
File đính kèm:
 chinh_phuc_ky_thi_thpt_quoc_gia_mon_toan_chuyen_de_van_dung.pdf
chinh_phuc_ky_thi_thpt_quoc_gia_mon_toan_chuyen_de_van_dung.pdf

