Chinh phục kỳ thi THPT Quốc gia môn Toán - Chuyên đề: Vận dụng cao môn Toán
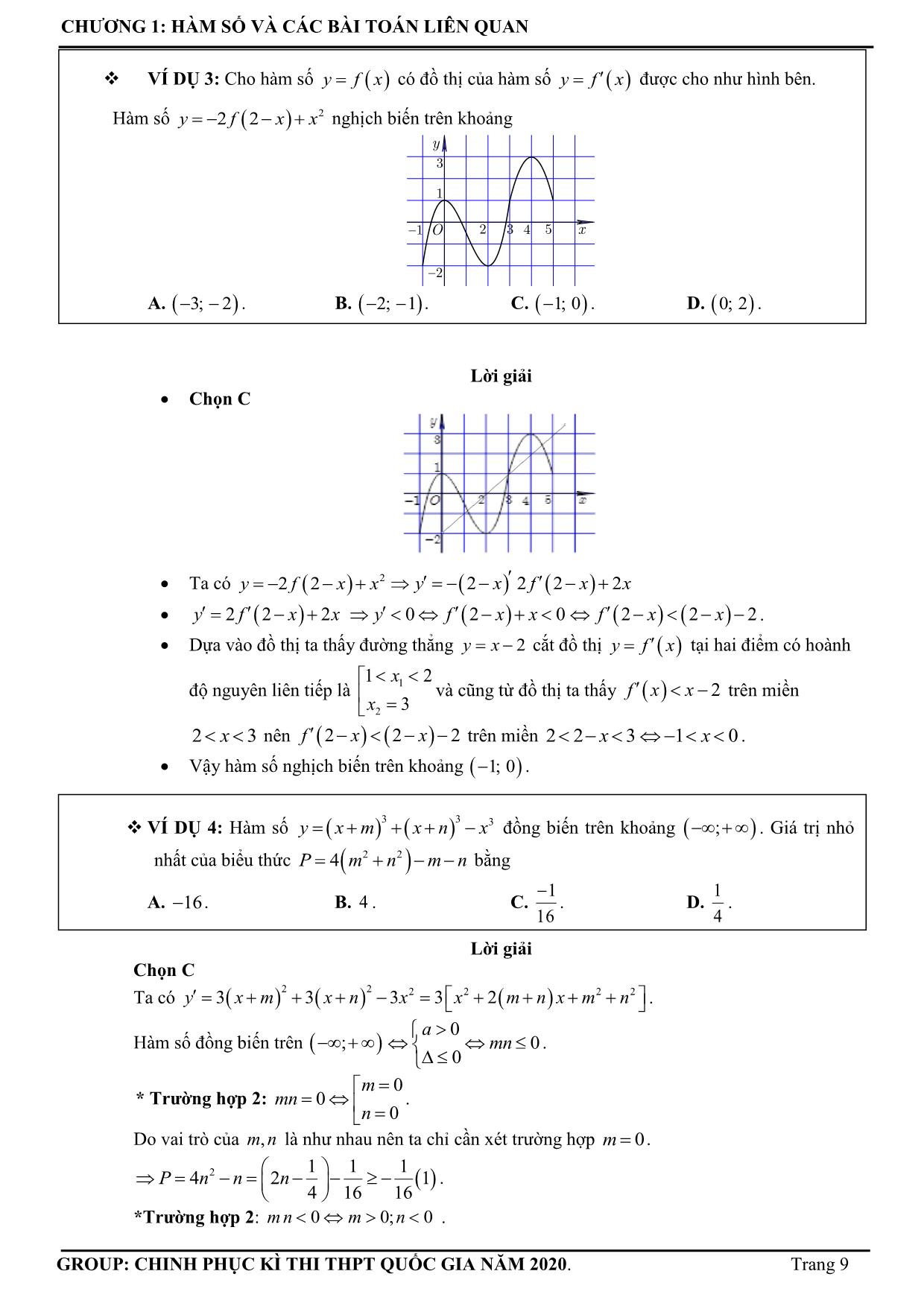
Có bao nhiêu mệnh đề đúng trong số các mệnh đề sau đối với hàm số g x f x 2 2 ?
I. Hàm số g x đồng biến trên khoảng 4; 2 .
II. Hàm số g x nghịch biến trên khoảng 0;2 .
III. Hàm số g x đạt cực tiểu tại điểm 2 .
IV. Hàm số g x có giá trị cực đại bằng 3.
A. 3. B. 2 . C. 1. D. 4 .
Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Chinh phục kỳ thi THPT Quốc gia môn Toán - Chuyên đề: Vận dụng cao môn Toán", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Chinh phục kỳ thi THPT Quốc gia môn Toán - Chuyên đề: Vận dụng cao môn Toán
12R . I2I1 BA Ta có 2 2 1 2 1 2 1 22 3 12 13 4 12 313 16T iz z AB I I R R . Vậy max 313 16T . Lời giải Chọn A Ta có 2 1 1 2 1iz i z i . Gọi 0 1 2z i có điểm biểu diễn là 1; 2I . Gọi A , B lần lượt là các điểm biểu diễn của 1z , 2z . Vì 1 2 2z z nên I là trung điểm của AB . Ta có 2 2 2 21 2 2 4 16 4z z OA OB OA OB OI AB . Dấu bằng khi OA OB . Lời giải Chọn B VÍ DỤ 1: Cho hai số phức 1z , 2z thỏa mãn 1 3 5 2z i và 2 1 2 4iz i . Tìm giá trị lớn nhất của biểu thức 1 22 3T iz z . A. 313 16 . B. 313 . C. 313 8 . D. 313 2 5 . VÍ DỤ 2: Giả sử 1z , 2z là hai trong số các số phức z thỏa mãn 2 1iz i và 1 2 2z z . Giá trị lớn nhất của 1 2z z bằng A. 4 . B. 2 3 . C. 3 2 . D. 3 . VÍ DỤ 3: Cho hai số phức u , v thỏa mãn 3 6 3 1 3 5 10u i u i , 1 2v i v i . Giá trị nhỏ nhất của u v là: A. 10 3 B. 2 10 3 C. 10 D. 5 10 3 GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 237 CHƯƠNG 3: SỐ PHỨC Ta có: 3 6 3 1 3 5 10u i u i 5 10 6 1 3 3 u i u i 1 2 5 10 3 MF MF . u có điểm biểu diễn M thuộc elip với hai tiêu điểm 1 20;6 , 1;3F F , tâm 1 9 ; 2 2 I và độ dài trục lớn là 5 10 2 3 a 5 10 6 a . 1 2 1 21; 3 : 3 6 0F F F F x y . Ta có: 1 2v i v i v i NA NB v có điểm biểu diễn N thuộc đường thẳng d là trung trực của đoạn AB với 1; 2 , 0;1A B . 1;3AB , 1 1 ; 2 2 K là trung điểm của AB : 3 2 0d x y . 22 1 27 2 3 102 2 , 21 3 d I d Dễ thấy 1 2F F d 2 10 min min , 3 u v MN d I d a . VÍ DỤ 4: Xét các số phức z a bi ( ,a b ) thỏa mãn 3 2 2z i . Tính a b khi 1 2 2 2 5z i z i đạt giá trị nhỏ nhất. A. 4 3 . B. 2 3 . C. 3 . D. 4 3 . Lời giải Chọn D Cách 1: Đặt 3 2z i w với w x yi ,x y . Theo bài ra ta có 2 22 4w x y . Ta có 2 2 221 2 2 2 5 4 2 1 3 4 2 1 3P z i z i w w i x y x y 2 2 2 2 20 8 2 1 3 2 5 2 2 1 3x x y x x y 2 2 2 2 22 2 22 2 1 1 3 2 1 1 3x y x x y x y x y 2 3 2 3 6y y y y . 2 2 1 1 6 3 0 3 4 x x P y y y x y . Vậy GTNN của P là bằng 6 đạt được khi 2 2 3z i . Cách 2: V ũ V ă n B ắ c GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 238 CHƯƠNG 3: SỐ PHỨC 3 2 2z i 2MI ;2M I với 3;2I . 1 2 2 2 5 2P z i z i MA MB với 1;2A , 2;5B . Ta có 2IM ; 4IA . Chọn 2;2K thì 1IK . Do đó ta có 2.IA IK IM IA IM IM IK IAM và IMK đồng dạng với nhau 2 AM IM MK IK 2AM MK . Từ đó 2P MA MB 2 MK MB 2BK . Dấu bằng xảy ra khi và chỉ khi M , K , B thẳng hàng và M thuộc đoạn thẳng BK . Từ đó tìm được 2;2 3M . Cách 3: Gọi ;M a b là điểm biểu diễn số phức .z a bi Đặt 3;2I , 1;2A và 2;5B . Ta xét bài toán: Tìm điểm M thuộc đường tròn C có tâm I , bán kính 2R sao cho biểu thức 2P MA MB đạt giá trị nhỏ nhất. Trước tiên, ta tìm điểm ;K x y sao cho 2MA MK M C . Ta có 2 2 2 22 4 4MA MK MA MK MI IA MI IK 2 2 2 2 2 2 22 . 4 2 . 2 4 3 4MI IA MI IA MI IK MI IK MI IA IK R IK IA * . * luôn đúng 2 2 2 4 0 3 4 0 IA IK M C R IK IA . 4 3 4 2 4 0 24 2 0 x x IA IK yy . Thử trực tiếp ta thấy 2;2K thỏa mãn 2 2 23 4 0R IK IA . Vì 2 2 2 21 3 10 4BI R nên B nằm ngoài C . Vì 2 21 4KI R nên K nằm trong C . Ta có 2 2 2 2 2MA MB MK MB MK MB KB . Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi M thuộc đoạn thẳng BK . Do đó 2MA MB nhỏ nhất khi và chỉ khi M là giao điểm của C và đoạn thẳng .BK Phương trình đường thẳng : 2BK x . Phương trình đường tròn 2 2 : 3 2 4C x y . Tọa độ điểm M là nghiệm của hệ 2 2 2 2 3 2 4 2 3 x x x y y hoặc 2 2 3 x y . Thử lại thấy 2;2 3M thuộc đoạn BK . Vậy 2a , 2 3b 4 3a b . VÍ DỤ 5: Gọi n là số các số phức z đồng thời thỏa mãn i 1 2i 3z và biểu thức 2 5 2i 3 3iT z z đạt giá trị lớn nhất. Gọi M là giá trị lớn nhất của T . Giá trị tích của .M n là A. 10 21 B. 6 13 C. 5 21 D. 2 13 GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 239 CHƯƠNG 3: SỐ PHỨC Lời giải Chọn A Gọi iz x y , với ,x y . Khi đó ;M x y là điểm biểu diễn cho số phức z . Theo giả thiết, i 1 2i 3z 2 i 3z 2 2 2 1 9x y . Ta có 2 5 2i 3 3iT z z 2 3MA MB , với 5; 2A và 0;3B . Nhận xét rằng A , B , I thẳng hàng và 2 3IA IB . Cách 1: Gọi là đường trung trực của AB , ta có : 5 0x y . 2 3T MA MB PA PB . Dấu “ ” xảy ra khi M P hoặc M Q . Giải hệ 2 2 5 0 2 1 9 x y x y 8 2 2 2 ; 2 2 P và 8 2 2 2 ; 2 2 Q . Khi đó max 5 21M T . Vậy . 10 21M n . Cách 2: Ta có A , B , I thẳng hàng và 2 3IA IB nên 2 3 0IA IB . 2 22 3MA MB 2 2 2 3MI IA MI IB 2 2 25 2 3MI IA IB 105 . Do đó 2 2 2. 2 3. 3T MA MB 2 25 2 3MA MB 525 hay 5 21T . Khi đó max 5 21M T . Dấu “ ” xảy ra khi M P hoặc M Q . Vậy . 10 21M n . BÀI TẬP RÈN LUYỆN CÂU 1: Trong các số phức z thỏa mãn 2 1 2z z gọi 1z và 2z lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Khi đó môđun của số phức 1 2w z z là A. 2 2w . B. 2w . C. 2w . D. 1 2w . CÂU 2. Cho số phức z và w thỏa mãn 3 4z w i và 9z w . Tìm giá trị lớn nhất của biểu thức T z w . A. max 176T . B. max 14T . C. max 4T . D. max 106T . CÂU 3: số phức z thỏa mãn 1 2 1 2 4 2i z i z . Gọi maxm z , minn z và số phức w m ni . Tính 2018 w A. 10094 . B. 10095 . C. 10096 . D. 10092 . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 240 CHƯƠNG 3: SỐ PHỨC CÂU 4: Cho số phức z thỏa mãn 5 1 3 3 1z i z i z i . Tìm giá trị lớn nhất M của 2 3z i ? A. 10 3 M B. 1 13M C. 4 5M D. 9M Chọn C CÂU 5: Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của z i P z , với z là số phức khác 0 và thỏa mãn 2z . Tính tỷ số M m . A. 5 M m B. 3 M m C. 3 4 M m D. 1 3 M m CÂU 6: Cho số phức z thỏa mãn 1 1z i , số phức w thỏa mãn 2 3 2w i . Tìm giá trị nhỏ nhất của z w . A. 13 3 B. 17 3 C. 17 3 D. 13 3 CÂU 7: Cho số phức z thỏa 1z . Gọi m , M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức 5 3 46 2 1P z z z z . Tính M m . A. 4m , 3n . B. 4m , 3n C. 4m , 4n . D. 4m , 4n . CÂU 8: Cho hai số phức 1 2,z z thỏa mãn 1 1 2z i và 2 1z iz . Tìm giá trị nhỏ nhất m của biểu thức 1 2z z ? A. 2 1m . B. 2 2m . C. 2m . D. 2 2 2m . CÂU 9: Xét các số phức z a bi , ,a b thỏa mãn 2 4 15 1z z i i z z . Tính 4F a b khi 1 3 2 z i đạt giá trị nhỏ nhất A. 7F . B. 6F . C. 5F . D. 4F . CÂU 10: Cho số phức z thỏa mãn 1z . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 21 1P z z z . Giá trị của .M m bằng A. 13 3 4 . B. 13 3 8 . C. 3 3 . D. 3 3 8 . CÂU 11: Cho hai số phức 1z , 2z thỏa mãn 1 3 5 2z i và 2 1 2 4iz i . Tìm giá trị lớn nhất của biểu thức 1 22 3T iz z . A. 313 16 . B. 313 . C. 313 8 . D. 313 2 5 . CÂU 12: Cho số phức 1z , 2z thỏa mãn 1 12z và 2 3 4i 5z . Giá trị nhỏ nhất của 1 2z z là: A. 0 . B. 2 C. 7 D. 17 CÂU 13: các số phức z thỏa mãn 4 3 2 z i . Giả sử biểu thức P z đạt giá trị lớn nhất, giá trị nhỏ nhất khi z lần lượt bằng 1 1 1 z a b i 1 1, a b và 2 2 2 z a b i 2 2, a b . Tính 1 2 S a a A. 4 S . B. 6 S . C. 8 S . D. 10 S . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 241 CHƯƠNG 3: SỐ PHỨC CÂU 14: Cho các số phức z thỏa mãn 2 4 2 1 2 z z i z i . Tìm giá trị nhỏ nhất của 3 2 P z i . A. min 4 P . B. min 2 P . C. min 7 2 P . D. min 3 P . CÂU 15: Cho các số phức z thỏa mãn 1 8 3 53 z i z i . Tìm giá trị lớn nhất của 1 2 P z i . A. max 53 P . B. max 185 2 P . C. max 106 P . D. max 53 P . CÂU 16: Cho số phức z thỏa mãn 2z . Giá trị nhỏ nhất của biểu thức 2 1 2 1 4P z z z z i bằng: A. 4 2 3 . B. 2 3 . C. 14 4 15 . D. 7 2 15 . GIẢI CHI TIẾT CÂU 1: Chọn B Đặt z a bi ,a b thì 2 1 2z z 2 1 2a bi a bi 2 2 1 2 2a b abi a bi 2 2 2 2 2 2 21 4 4a b a b a b 4 4 2 2 2 21 2 6 2 0a b a b a b 2 2 2 21 4 0a b b 2 2 2 21 2 1 2 0a b b a b b 2 2 2 2 1 2 0 1 2 0 a b b a b b TH1: 2 2 1 2 0a b b 22 1 2a b . Khi đó tập hợp điểm ;M a b biểu diễn số phức z là đường tròn có tâm 1 0;1I , bán kính 2R , giao điểm của OI (trục tung) với đường tròn là 1 0; 2 1M và 2 0;1 2M 2 1 1 2w i i 2w i 2w TH2: 2 2 1 2 0a b b 22 1 2a b . Khi đó tập hợp điểm ;M a b biểu diễn số phức z là đường tròn có tâm 2 0; 1I , bán kính 2R , giao điểm của OI (trục tung) với đường tròn là 3 0; 2 1M và 4 0; 2 1M 2 1 1 2w i i 2w i 2w . CÂU 2. Chọn D Đặt ,z x yi x y . Do 3 4z w i nên 3 4w x y i . Mặt khác 9z w nên 2 2 2 22 3 2 4 4 4 12 16 25 9z w x y x y x y 2 22 2 6 8 28x y x y 1 . Suy ra 2 22 2 3 4T z w x y x y . Áp dụng bất đẳng thức Bunyakovsky ta có 2 2 22 2 2 6 8 25T x y x y 2 . Dấu " " xảy ra khi 2 22 2 3 4x y x y . Từ 1 và 2 ta có 2 2. 28 25 106 106T T . Vậy 106MaxT . CÂU 3: Chọn C GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 242 CHƯƠNG 3: SỐ PHỨC Ta có 1 2 1 2 4 2i z i z 1 1 4z i z i . Gọi M là điểm biểu diễn của số phức z , 1 1;1F là điểm biểu diễn của số phức 1 1z i và 2 1; 1F là điểm biểu diễn của số phức 2 1z i . Khi đó ta có 1 2 4MF MF . Vậy tập hợp điểm M biểu diễn số phức z là Elip nhận 1F và 2F làm hai tiêu điểm. Ta có 1 2 2 2 2 2 2F F c c c . Mặt khác 2 4 2a a suy ra 2 2 4 2 2b a c . Do đó Elip có độ dài trục lớn là 1 2 2 4A A a , độ dài trục bé là 1 2 2 2 2B B b . Mặt khác O là trung điểm của AB nên m max z maxOM 1OA 2a và n min z minOM 1 2OB b . Do đó 2 2w i suy ra 6w 2018 10096w . CÂU 4: Gọi 0;1A , 1;3 , 1; 1B C . Ta thấy A là trung điểm của BC 2 2 2 2 2 4 MB MC BC MA 2 2 2 2 22 2 10 2 BC MB MC MA MA . Ta lại có : 5 1 3 3 1z i z i z i 2 25 3 10.MA MB MC MB MC 2 225 10 2 10MA MA 2 5MC Mà 2 3 2 4z i z i i 2 4z i i 2 5 4 5z i . Dấu " " xảy ra khi 2 5 1 2 4 z i a b , với z a bi ; , a b . 2 3 2 5 z i loai z i . CÂU 5: Chọn B Gọi 1 z i T T z i z . Nếu 1T Không có số phức nào thoả mãn yêu cầu bài toán. Nếu 1 1 2 1 1 1 2 i i T z z T T T . Vậy tập hợp điểm biểu diễn số phức T là hình tròn tâm 1;0I có bán kính 1 2 R . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 243 CHƯƠNG 3: SỐ PHỨC 3 2 1 2 M OB OI R m OA OI R 3 M m . CÂU 6: Chọn B Gọi ;M x y biểu diễn số phức z x iy thì M thuộc đường tròn 1C có tâm 1 1;1I , bán kính 1 1R . ;N x y biểu diễn số phức w x iy thì N thuộc đường tròn 2C có tâm 2 2; 3I , bán kính 2 2R . Giá trị nhỏ nhất của z w chính là giá trị nhỏ nhất của đoạn MN . Ta có 1 2 1; 4I I 1 2 17I I 1 2R R 1C và 2C ở ngoài nhau. minMN 1 2 1 2I I R R 17 3 CÂU 7: Chọn A Vì 1z và 2 .z z z nên ta có 1 z z . Từ đó, 5 3 46 2 1P z z z z 4 4 46 2 1z z z z 4 4 46 2 1z z z . Đặt 4z x iy , với ,x y . Do 1z nên 4 2 2 1z x y và 1 , 1x y . Khi đó 6 2 1P x iy x iy x iy 2 22 6 2 1x x y 2 6 2 2 2x x 2 2 2 1 3x . Do đó 3P . Lại có 1 1x 0 2 2 2x 1 2 2 1 1x 4P . Vậy 4M khi 4 1z và 3m khi 4 1 3 i 2 2 z . Suy ra 1M m . CÂU 8: Chọn D Đặt 1 ; ,z a bi a b 2z b ai 1 2z z a b b a i . Nên 2 2 1 2 12.z z a b b a z Ta lại có 1 1 12 1 1 2z i z i z 1 2 2z . Suy ra 1 2 12. 2 2 2z z z . Dấu " " xảy ra khi 0 1 1 a b . Vậy 1 2min 2 2 2m z z . CÂU 9: Chọn A Ta có 2 4 15 1z z i i z z 2 4 15 1a bi a bi i i a bi a bi 2 8 15 2 1b a suy ra 15 8 b . 2 2 2 21 1 1 13 2 1 2 6 8 15 4 24 36 4 32 21 2 2 2 2 z i a b b b b b b GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 244 CHƯƠNG 3: SỐ PHỨC Xét hàm số 24 32 21f x x x với 15 8 x 15 8 32 0, 8 f x x x suy ra f x là hàm số đồng biến trên 15 ; 8 nên 15 4353 8 16 f x f . Do đó 1 3 2 z i đạt giá trị nhỏ nhất bằng 1 4353 2 16 khi 15 1 ; 8 2 b a . Khi đó 4 7F a b . CÂU 10: Chọn A Đặt 1 1 2t z z nên 0;2t . Do 1z nên . 1z z 21 . 1 1P z z z z z z z z . Ta có 22 1 1 1 . 1 2t z z z z z z z z z nên 2 2z z t . Vậy 2 3P f t t t , với 0;2t . Khi đó, 2 2 3 khi 3 2 3 khi0 3 t t t f t t t t nên 2 1 khi 3 2 2 1 khi0 3 t t f t t t . 0f t 1 2 t . 0 3f ; 1 13 2 4 f ; 3 3f ; 2 3f . Vậy 13 4 M ; 3m nên 13 3 . 4 M m . CÂU 11: Chọn A Ta có 1 13 5 2 2 6 10 4z i iz i 1 ; 2 21 2 4 3 6 3 12iz i z i 2 . Gọi A là điểm biểu diễn số phức 12iz , B là điểm biểu diễn số phức 23z . Từ 1 và 2 suy ra điểm A nằm trên đường tròn tâm 1 6; 10I và bán kính 1 4R ; điểm B nằm trên đường tròn tâm 2 6;3I và bán kính 2 12R . I2I1 BA Ta có 2 2 1 2 1 2 1 22 3 12 13 4 12 313 16T iz z AB I I R R . Vậy max 313 16T . CÂU 12: Chọn B Gọi 1 1 1iz x y và 2 2 2iz x y , trong đó 1x , 1y , 2x , 2y ; đồng thời 1 1 1;M x y và 2 2 2;M x y lần lượt là điểm biểu diễn các số phức 1z , 2z . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 245 CHƯƠNG 3: SỐ PHỨC Theo giả thiết, ta có: 2 2 1 1 2 2 2 2 144 3 4 25 x y x y . Do đó 1M thuộc đường tròn 1C có tâm 0;0O và bán kính 1 12R , 2M thuộc đường tròn 2C có tâm 3;4I và bán kính 2 5R . Mặt khác, ta có 2 1 25 7 O C OI R R nên 2C chứa trong 1C . (C2) (C1) M2 O M1 I Khi đó 1 2z z 1 2M M . Suy ra 1 2 1 2 minminz z M M 1 2 1 22 2M M R R . CÂU 13: Chọn C Gọi z a bi , , a b 4 3 2 4 3 2 4 3 2 z i a ib i a b i 2 2 4 3 4 a b Khi đó tập hợp các điểm ;M a b biểu diễn số phức z a bi thuộc vào đường tròn C có tâm 4; 3 I , 2 R . Ta có 2 23 4 5 OI . Suy ra max 5 2 7 z OI R , min 5 2 3 z OI R . Gọi là đường thẳng qua hai điểm OI ta có phương trình của :3 4 0 x y . Gọi M và N lần lượt là hai giao điểm của và C sao cho 3 OM và 7 ON khi đó 3 12 9 ; 5 5 5 7 28 21 ; 5 5 5 OM OI M ON OI N 1 2 28 21 5 5 12 9 5 5 z i z i 28 12 8 5 5 S . CÂU 14: Chọn D Ta có 2 4 2 1 2 z z i z i 2 2 1 2 0 z i z i z i 2 0 2 1 2 z i z i z i . Do đó tập hợp các điểm N biểu diễn số phức z trên mặt phẳng tọa độ Oxy là điểm 0;2A và đường trung trực của đoạn thẳng BC với 0; 2 B , 1; 2 C . Ta có 1;0 BC , 1 ;0 2 M là trung điểm BC nên phương trình đường trung trực của BC là : 2 1 0 x .Đặt 3;2 D , 3 DA , 7 , 2 d D . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 246 CHƯƠNG 3: SỐ PHỨC Khi đó 3 2 P z i DN , với N là điểm biểu diễn cho z . Suy ra min min , , 3 P DA d D . CÂU 15: Chọn C Xét 1;1 , 8;3A B ta có 53 AB các điểm biểu diễn z là đoạn thẳng AB 1 2 P z i MM với M là điểm biểu diễn số phức z , M là điểm biểu diễn số phức 1 2 z i Phương trình đường thẳng : 2 7 5 0 AB x y Hình chiếu vuông góc của M lên AB là 1 87 13 ; 53 53 M Ta có A nằm giữa 1M và B nên P MM lớn nhất 1 MM lớn nhất 8 3 M B z i max 106 P . CÂU 16: Chọn A Gọi i, ,z x y x y . Theo giả thiết, ta có 2 22 4z x y . Suy ra 2 , 2x y . Khi đó, 2 1 2 1 4P z z z z i 2 22 22 1 1 2x y x y y 2 22 22 1 1 2P x y x y y 22 2 1 2y y . Dấu “ ” xảy ra khi 0x . Xét hàm số 22 1 2f y y y trên đoạn 2; 2 , ta có: 2 2 1 1 y f y y 2 2 2 1 1 y y y ; 1 0 3 f y y . Ta có 1 2 3 3 f ; 2 4 2 5f ; 2 2 5f . Suy ra 2; 2 min 2 3f y khi 1 3 y . Do đó 2 2 3 4 2 3P . Vậy min 4 2 3P khi 1 i 3 z . GROUP: CHINH PHỤC KÌ THI THPT QUỐC GIA NĂM 2020. Trang 247
File đính kèm:
 chinh_phuc_ky_thi_thpt_quoc_gia_mon_toan_chuyen_de_van_dung.pdf
chinh_phuc_ky_thi_thpt_quoc_gia_mon_toan_chuyen_de_van_dung.pdf

