Chẩn đoán lỗi máy biến áp sử dụng GeNIe Modeler

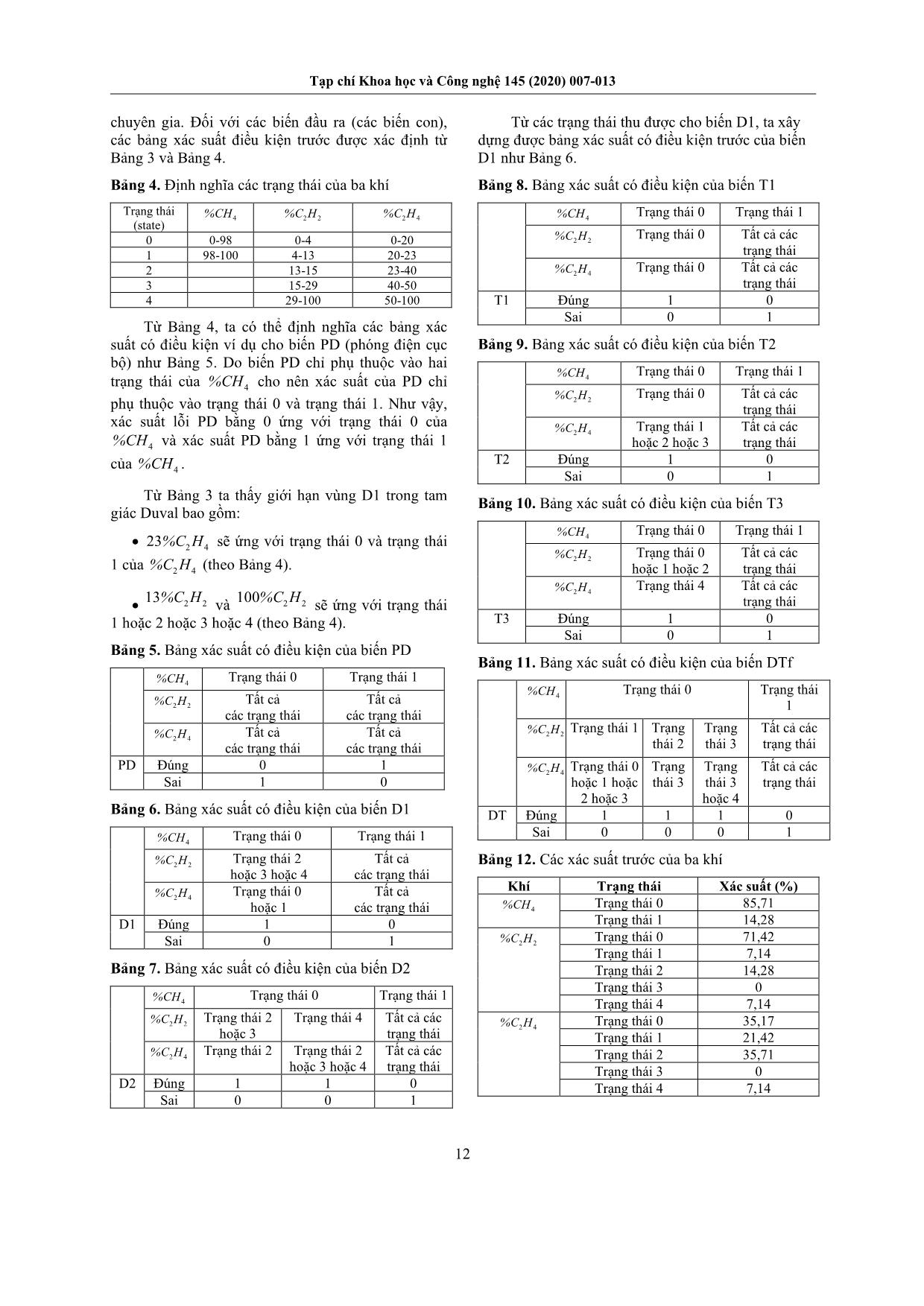
tượng không khởi động được của laptop. Câu hỏi này 
được trả lới bằng cách tính các xác suất bằng các 
phương trình toán học sau đây. 
Tính toán xác suất: Giả thiết ta cần tính các xác 
suất có điều kiện P B loaded | S True và 
 P M deg raded | S True . Quan hệ giữa các xác 
suất có điều kiện và xác suất liên kết được xác định 
theo phương trình sau: 
 , | |P a b P a b P b P b a P a (2) 
Phương trình (2) dẫn đến công thức Bayes nổi 
tiếng như sau: 
|
|
P b a P a
P a b
P b
 (3) 
Phương trình (2) có thể được biểu diễn dưới 
dạng tổng quát như sau: 
| , |
| ,
|
P b a c P a c
P a b c
P b c
 (4) 
Theo phương trình (1) ta có: 
P B loaded | S True
P B loaded,S True
P S True
M ok ,deg raded
M ok ,deg raded S true, fault
P S True,M ,B loaded
P S True,M ,B

 
 (5) 
Tử số của phân số (5) là tổng của hai xác suất 
kết hợp như sau: 
M ok ,deg raded
P S True,M ,B loaded
P S True,M ok ,B loaded
P S True,M deg raded ,B loaded

Trong đó: 
0 05 0 95 0 9 0 0428
P S True,M ok ,B loaded
P S True | M ok ,B loaded
P M ok | B loaded
P B loaded
, , , ,
0 9 0 05 0 9 0 0405
P S True,M deg raded ,B loaded
P S True | M deg raded ,B loaded
P M deg raded | B loaded
P B loaded
, , , ,
Mẫu số của phân số (5) là tổng của bốn xác suất 
kết hợp như sau: 
M ok ,deg raded S true, fault
P S True,M ,B
P S True,M ok ,B loaded
P S True,M deg raded ,B loaded
P S True,M ok ,B not _ loaded
P S True,M deg raded ,B not _ loaded
 
Trong đó: 
 0 0428P S True,M ok ,B loaded , 
 0 0405P S True,M deg raded ,B loaded , 
1 0 95 0 1 0 095
P S True,M ok ,B not _ loaded
P S True | M ok ,B not _ loaded
P M ok | B not _ loaded
P B not _ loaded
, , ,
Tạp chí Khoa học và Công nghệ 145 (2020) 007-013 
10 
1 0 05 0 1 0 005
P S True,M deg raded ,B not _ loaded
P S True | M deg raded ,B not _ loaded
P M deg raded | B not _ loaded
P B not _ loaded
, , ,
Cuối cùng ta có: 
0 0428 0 0405
0 0428 0 0405 0 095 0 005
0 4543
P B loaded | S True
, ,
, , , ,
,
 1 0 4543 0 5457P B not _ loaded | S True , , 
Tương tự, ta tính được các xác suất điều kiện 
như sau: 
 0 7517P M ok | S True , 
 0 2483P M deg raded | S True , 
Từ các xác suất được tính toán ở trên, ta có nhận 
xét như sau: Khi quan sát thấy bằng chứng là laptop 
không khởi động được ( S True ), xác suất của pin 
được nạp là 0,4543 và xác suất của pin không được 
nạp là 0,5457. Do đó, nguyên nhân làm cho laptop 
không khởi động được có thể là do pin không được 
nạp (do xác suất của pin không được nạp cao hơn xác 
suất pin được nạp). Tương tự, khi quan sát thấy bằng 
chứng là laptop không khởi động được ( S True ), 
xác suất của bo mạch mẹ bình thường là 0,7517 và 
xác suất của bo mạch mẹ xuống cấp là 0,2483. Do đó, 
nhiều khả năng bo mạch mẹ vẫn bình thường (do xác 
suất của bo mạch mẹ bình thường cao hơn xác suất bo 
mạch mẹ bị xuống cấp). 
3. GeNIe Modeler 
GeNIe Modeler là một phần mềm phát triển bởi 
công ty BayesFusion, LLC (Hoa Kỳ). Phần mềm này 
có thể tải về miễn phí từ địa chỉ sau: 
https://www.bayesfusion.com/downloads/ 
Với một giao diện đồ họa, người sử dụng có thể 
phát triển các ứng dụng phức tạp của mạng Bayes 
trong GeNIe Modeler với các bước suy luận như đã 
đề cập trong phần 2 mà không mất nhiều thời gian 
phải làm quen với công cụ này. GiNIe Modeler có thể 
được xem như là một công cụ lý tưởng để triển khai 
các mô hình chẩn đoán lỗi của các hệ thống sử dụng 
mạng Bayes bao gồm chẩn đoán lỗi của thiết bị điện 
như máy biến áp dầu sẽ đề cập chi tiết trong phần sau. 
Tính năng của GeNIe Modeler bao gồm: 
 Trình soạn thảo đồ họa để tạo / tìm hiểu / tinh 
chỉnh các mô hình mạng. 
 Hoàn thành tích hợp với MS Excel, cắt và dán 
dữ liệu vào chế độ xem bảng tính nội bộ của GeNIe. 
 Mở nhiều mạng và cắt và dán các phần của mô 
hình giữa chúng. 
 Xử lý dữ liệu linh hoạt, bao gồm nhập từ cơ sở 
dữ liệu bên ngoài. 
 Bao gồm các thuật toán học cấu trúc và tham số. 
 Hỗ trợ các nút phương trình và phân phối xác 
suất liên tục trong các mô hình liên tục và lai. 
 Hỗ trợ quản lý trường hợp (lưu và truy xuất 
nhiều bộ bằng chứng). 
 Tương thích chéo với các phần mềm khác. Hỗ 
trợ tất cả các loại tệp mạng Bayes chính (ví dụ: 
Hugin, Netica, Ergo). 
Hình 2 là mạng Bayes trong GeNIe cho bài toán 
không khởi động được của một laptop. Sau khi quan 
sát được hiện tượng laptop không khởi động được 
( S True ), GeNIe Modeler cho phép tính được xác 
suất có điều kiện như Hình.2: 
 75P M ok | S True % 
 25P M deg raded | S True % 
 45P B loaded | S True % 
 55P B not _ loaded | S True % 
Hình 2. Mạng Bayes trong GeNIe Modeler. 
4. Ứng dụng của GeNIe Modeler trong chẩn đoán 
lỗi máy biến áp dầu 
Máy biến áp là một thiết bị điện quan trọng 
trong các hệ thống truyền tải và phân phối điện. Để 
cải thiện độ tin cậy của máy biến áp và giảm chi phí 
cho công tác bảo trì, các kỹ thuật chẩn đoán và theo 
dõi là rất cần thiết. Dây quấn của máy biến áp bao 
gồm cách điện bằng giấy được ngâm trong dầu cách 
điện, do đó các cách điện giấy và dầu cách điện được 
xem như là đối tượng chính dùng cho việc phát hiện 
các sự cố. 
Phân tích khí hòa tan của dầu cách điện máy 
biến áp được xem như là một kỹ thuật hiển thị tốt 
nhất về điều kiện tổng thể của một máy biến áp và 
được sử dụng rộng rãi nhất trong chẩn đoán lỗi của 
Tạp chí Khoa học và Công nghệ 145 (2020) 007-013 
11 
máy biến áp. Do các ứng xuất nhiệt và điện, sự phân 
ly của giấy và dầu dẫn tới các lỗi nghiêm trọng. Một 
số khí thoát ra do quá trình phân ly làm giảm cường 
độ cách điện và khả năng giảm nhiệt của dầu máy 
biến áp. Ethane (C2H6), methane (CH4), hydrogen 
(H2), acetylene (C2H2) và ethylene (C2H4) là các khí 
tạo ra do phân ly của dầu. Carbon dioxide (CO2) và 
carbon monoxide (CO) được tạo ra do phân ly của 
giấy. 
Các lỗi bên trong của máy biến áp có thể được 
chia thành hai nhóm: (1) nhóm các lỗi nhiệt và (2) 
nhóm các lỗi điện. 
 Nhóm các lỗi nhiệt: Lỗi dầu (C2H4, C2H6), 
giấy (CO, CO2). 
 Nhóm các lỗi điện: Phóng điện cục bộ (H2, 
CH4), hồ quang (C2H2). 
Ngoại trừ khí CO và CO2, các khí còn lại sinh ra 
do sự phân ly của dầu. Tỷ lệ CO/CO2 có thể được sử 
dụng để đánh giá sự xuống cấp của cách điện giấy. 
Phương pháp tam giác Duval là một công cụ 
phân tích khí hòa tan được xây dựng bằng kinh 
nghiệm từ đầu những năm 1970 và được sử dụng bởi 
IEC. Phương pháp này đã chứng tỏ được hiệu quả và 
do đó được sử dụng rộng rãi. 
Bảng 2. Các kiểu lỗi và các mã kết hợp 
Kiểu lỗi Mã 
Phóng điện cục bộ PD 
Phóng điện năng lượng thấp D1 
Phóng điện năng lượng cao D2 
Các lỗi nhiệt T<300oC T1 
Các lỗi nhiệt 300oC<T<700oC T2 
Các lỗi nhiệt T>700oC T3 
Hỗn hợp của các lỗi điện và nhiệt DT 
Hình 3. Tam giác Duval. 
Phương pháp tam giác Duval sử dụng các giá trị 
của ba khí: CH4, C2H2 và C2H4 và vị trí của chúng 
trong một tam giác như Hình.3. Bên trong tam giác 
có bảy vùng lỗi bao gồm lỗi phóng điện cục bộ, các 
lỗi nhiệt với các dải nhiệt độ khác nhau và hồ quang 
điện. Các kiểu lỗi và các mã kết hợp được trình bày 
trong Bảng 2. 
Các công thức sau đây xác định ba tọa độ của 
tam giác Duval dựa trên kết quả phân tích khí: 
 2 2 100
a
C H %
a b c
 (6) 
 2 4 100
b
C H %
a b c
 (7) 
 4 100
c
CH %
a b c
 (8) 
Trong đó: 
 2 2a C H ppm , 2 4b C H ppm , 4c CH ppm 
Bảng 3 là các giới hạn các vùng trong tam giác 
Duval. Để tìm các lỗi dùng tam giác Duval, trước tiên 
chúng ta tính phần trăm của các khí theo (6), (7) và 
(8). Tiếp đó, vẽ đường thẳng của đại lượng 4%CH 
song song với cạnh 2 2C H , vẽ đường thẳng của đại 
lượng 2 4%C H song song với cạnh 4CH và vẽ đường 
thẳng 2 2%C H song song với cạnh 2 4C H . Giao của 
ba đường sẽ xác định lỗi cho các kết quả phân tích 
khí hòa tan trong máy biến áp. 
Bảng 3. Giới hạn các vùng lỗi trong tam giác Duval 
PD 498%CH 4100%CH 
D1 2 423%C H 2 213%C H 2 2100%C H 
D2 2 423%C H 2 440%C H 2 213%C H 2 229%C H 
T1 2 24%C H 2 420%C H 
T2 2 24%C H 2 420%C H 2 450%C H 
T3 2 215%C H 2 450%C H 2 4100%C H 
DT 2 24%C H 2 213%C H 2 215%C H 2 229%C H 
 2 440%C H 2 450%C H 
Theo các giá trị tính theo phần trăm của giới hạn 
của các vùng lỗi (từ Bảng 3), ta có thể định nghĩa các 
trạng thái của ba khí như Bảng 4. 
Cấu trúc của một mạng Bayes dùng để chẩn 
đoán lỗi sẽ có dạng như Hình 4. Mạng có 3 biến đầu 
vào ứng với các phần trăm của ba khí và có 7 biến 
đầu ra ứng với 7 loại sự cố khác nhau. Các trạng thái 
khác nhau của 3 biến đầu vào có thể quan sát được 
hay nói cách khác các bằng chứng của các đầu vào có 
thể thu được qua tam giác Duval. Đối với các biến 
đầu vào (các biến cha mẹ), các xác suất cận biên 
trước có thể thu được từ kinh nghiệm hoặc kiến thức 
Tạp chí Khoa học và Công nghệ 145 (2020) 007-013 
12 
chuyên gia. Đối với các biến đầu ra (các biến con), 
các bảng xác suất điều kiện trước được xác định từ 
Bảng 3 và Bảng 4. 
Bảng 4. Định nghĩa các trạng thái của ba khí 
Trạng thái 
(state) 
4%CH 2 2%C H 2 4%C H 
0 0-98 0-4 0-20 
1 98-100 4-13 20-23 
2 13-15 23-40 
3 15-29 40-50 
4 29-100 50-100 
Từ Bảng 4, ta có thể định nghĩa các bảng xác 
suất có điều kiện ví dụ cho biến PD (phóng điện cục 
bộ) như Bảng 5. Do biến PD chỉ phụ thuộc vào hai 
trạng thái của 4%CH cho nên xác suất của PD chỉ 
phụ thuộc vào trạng thái 0 và trạng thái 1. Như vậy, 
xác suất lỗi PD bằng 0 ứng với trạng thái 0 của 
4%CH và xác suất PD bằng 1 ứng với trạng thái 1 
của 4%CH . 
Từ Bảng 3 ta thấy giới hạn vùng D1 trong tam 
giác Duval bao gồm: 
 2 423%C H sẽ ứng với trạng thái 0 và trạng thái 
1 của 2 4%C H (theo Bảng 4). 
 2 2
13%C H
 và 2 2
100%C H
 sẽ ứng với trạng thái 
1 hoặc 2 hoặc 3 hoặc 4 (theo Bảng 4). 
Bảng 5. Bảng xác suất có điều kiện của biến PD 
4%CH Trạng thái 0 Trạng thái 1 
2 2%C H Tất cả 
các trạng thái 
Tất cả 
các trạng thái 
2 4%C H Tất cả 
các trạng thái 
Tất cả 
các trạng thái 
PD Đúng 0 1 
Sai 1 0 
Bảng 6. Bảng xác suất có điều kiện của biến D1 
4%CH Trạng thái 0 Trạng thái 1 
2 2%C H Trạng thái 2 
 hoặc 3 hoặc 4 
Tất cả 
các trạng thái 
2 4%C H Trạng thái 0 
 hoặc 1 
Tất cả 
các trạng thái 
D1 Đúng 1 0 
Sai 0 1 
Bảng 7. Bảng xác suất có điều kiện của biến D2 
4%CH Trạng thái 0 Trạng thái 1 
2 2%C H Trạng thái 2 
hoặc 3 
Trạng thái 4 Tất cả các 
trạng thái 
2 4%C H Trạng thái 2 Trạng thái 2 
hoặc 3 hoặc 4 
Tất cả các 
trạng thái 
D2 Đúng 1 1 0 
Sai 0 0 1 
Từ các trạng thái thu được cho biến D1, ta xây 
dựng được bảng xác suất có điều kiện trước của biến 
D1 như Bảng 6. 
Bảng 8. Bảng xác suất có điều kiện của biến T1 
4%CH Trạng thái 0 Trạng thái 1 
2 2%C H Trạng thái 0 Tất cả các 
trạng thái 
2 4%C H Trạng thái 0 Tất cả các 
trạng thái 
T1 Đúng 1 0 
Sai 0 1 
Bảng 9. Bảng xác suất có điều kiện của biến T2 
4%CH Trạng thái 0 Trạng thái 1 
2 2%C H Trạng thái 0 Tất cả các 
trạng thái 
2 4%C H Trạng thái 1 
hoặc 2 hoặc 3 
Tất cả các 
trạng thái 
T2 Đúng 1 0 
Sai 0 1 
Bảng 10. Bảng xác suất có điều kiện của biến T3 
4%CH Trạng thái 0 Trạng thái 1 
2 2%C H Trạng thái 0 
hoặc 1 hoặc 2 
Tất cả các 
trạng thái 
2 4%C H Trạng thái 4 Tất cả các 
trạng thái 
T3 Đúng 1 0 
Sai 0 1 
Bảng 11. Bảng xác suất có điều kiện của biến DTf 
4%CH
Trạng thái 0 Trạng thái 
1 
2 2%C H
Trạng thái 1 Trạng 
thái 2 
Trạng 
thái 3 
Tất cả các 
trạng thái 
2 4%C H
Trạng thái 0 
hoặc 1 hoặc 
2 hoặc 3 
Trạng 
thái 3 
Trạng 
thái 3 
hoặc 4 
Tất cả các 
trạng thái 
DT Đúng 1 1 1 0 
Sai 0 0 0 1 
Bảng 12. Các xác suất trước của ba khí 
Khí Trạng thái Xác suất (%) 
4%CH Trạng thái 0 85,71 
Trạng thái 1 14,28 
2 2%C H Trạng thái 0 71,42 
Trạng thái 1 7,14 
Trạng thái 2 14,28 
Trạng thái 3 0 
Trạng thái 4 7,14 
2 4%C H Trạng thái 0 35,17 
Trạng thái 1 21,42 
Trạng thái 2 35,71 
Trạng thái 3 0 
Trạng thái 4 7,14 
Tạp chí Khoa học và Công nghệ 145 (2020) 007-013 
13 
Bằng cách lập luận tượng tự, ta thu được các 
Bảng 7, 8, 9, 10 và 11 là các bảng xác suất có điều 
kiện trước của 5 biến còn lại bao gồm D2, T1, T2, T3 
và DT. Ví dụ nếu %C2H2 bao gồm tất cả các trạng 
thái (từ trạng thái 0 đến trạng thái 4), %C2H4 bao gồm 
tất cả các trạng thái (từ trạng thái 0 đến trạng thái 4) 
và %CH4 chỉ bao gồm trạng thái 0 thì lỗi không phải 
là PD (phóng điện cục bộ). 
Chúng ta giả thiết các xác suất cận biên của ba 
biến đầu vào có dạng như Bảng 12 [5]. 
Hình.5 là một mạng Bayes với giao diện cột xác 
suất trong GeNIe Modeler dùng để chẩn đoán lỗi của 
máy biến áp. Thông số xác suất của 7 nút con ứng với 
7 lỗi của máy được xác định theo Bảng 5, 6, 7, 8, 9, 
10 và 11. Xác suất trước của 3 nút mẹ được xác định 
theo thực nghiệm [5]. Từ kết quả suy luận của mạng 
Bayes trong GeNIe Modeler ta thấy xác suất của biến 
T2 với trạng thái Đúng (True) là cao nhất với giá trị 
bằng 35%. Do đó, nhiều khả năng sự cố bắt nguồn từ 
các lỗi nhiệt nằm trong dải nhiệt độ từ 300oC đến 700 
oC. 
Hình 4. Mạng Bayes cho tam giác Duval trong GeNIe Modeler. 
Hình 5. Mạng Bayes cho tam giác Duval với giao diện của các cột xác suất trong GeNIe Modeler. 
5. Kết luận 
Tính mới về khoa học của bài báo là ứng dụng 
thành công một lý thuyết của trí tuệ nhân tạo (mạng 
Bayes) để chẩn đoán lỗi của máy biến áp dầu với kỹ 
thuật phân tích khí hòa tan. Mạng Bayes có thể sử 
dụng để dự báo khả năng của các lỗi của các hệ thống 
ở dưới dạng các xác suất của một cấu trúc mạng nhân 
quả. Hướng nghiên cứu tiếp theo của nghiên cứu này 
là ứng dụng phần mềm GeNIe Modeler với các 
phương pháp học cấu trúc và học tham số để từ đó có 
thể áp dụng cho chẩn đoán lỗi hiệu quả cho các đối 
tượng nghiên cứu khác. Thêm vào đó, kết quả của 
phương pháp đề cập trong bài báo này cần được so 
sánh với các kết quả của phương pháp khác bao gồm 
cả thực nghiệm. 
Lời cảm ơn 
Nghiên cứu này được tài trợ bởi Trường Đại học 
Bách khoa Hà Nội (HUST) trong đề tài mã số T2018-
PC-063. 
Tài liệu tham khảo 
[1] S.X.Ding, Model-based Fault Diagnosis Techniques-
Design Schemes, Algorithms, and Tools, 2008 
Springer-Verlag Berlin Heidenberg, ISBN 978-3-540-
76303-1. 
[2] Qi-Ping Yang, Meng-Qun Li, Xue-Yun Mu, Jun Wang, 
Application of Artificial Intelligence (AI) in Power 
Transformer Fault Diagnosis, 2009 International 
Conference on Artificial Intelligence and 
Computational Intelligence. 
[3] Xiaodong Yu, Hongzhi Zang, Transfomer fault 
diagnosis based on rough sets theory and artificial 
neural networks, 2008 International Conference on 
Condition Monitoring and Diagnosis. 
[4] Wang Yongqiang, Lu Fangcheng, Li Heming, The 
Fault Diagnosis Method for Electrical Equipment Using 
Bayesian Network, 2009 First International Workshop 
on Education Technology and Computer Science. 
[5] Abdelaziz Lakehal, Fouad Tachi, Hocine Cheghib, A 
new contribution for fault prediction of electrical power 
transformers, 2017 6th International Conference on 
Systems and Control (ICSC). 
[6] GeNIE: https://www.bayesfusion.com/genie/