Cải tiến thuật toán phân loại đa tín hiệu để ước lượng điện môi tương đối phức của vật liệu dựa trên phép đo phản xạ trong không gian tự do ở băng tần X

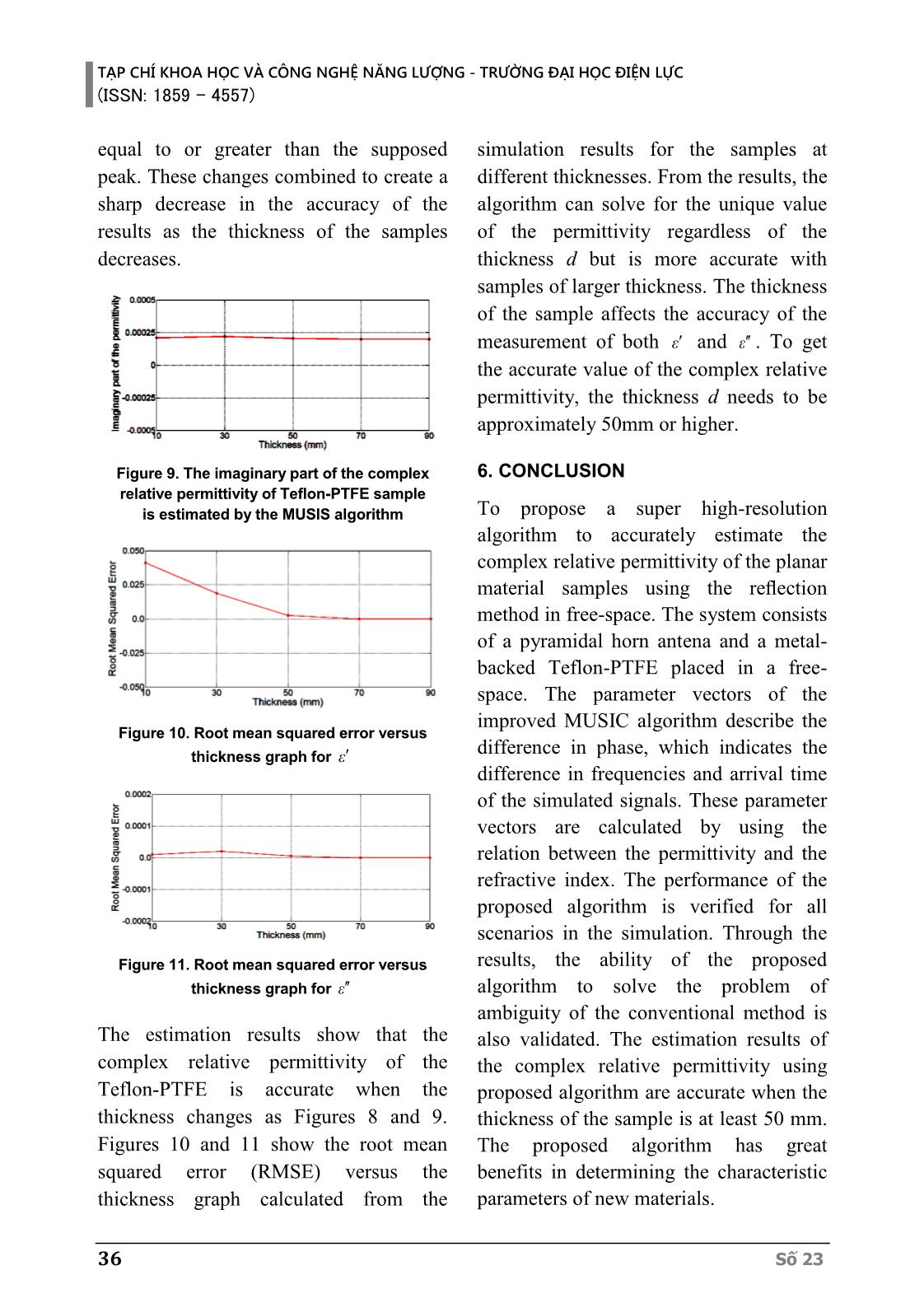
M
a
te
ri
a
l 
s
a
m
p
le
d
Free-space
d0
S11
Metal-backed
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 33 
space and material sample) at the first 
frequency and the thi frequency is: 
 i 0
4 ( 1)
Δ
π i - f
φ = d j d
c
 
 (6) 
Combine this with the phase difference, 
the equation (1) can be written using the 
vector notation as follows: 
X = AS +W (7) 
where: 
 1 2 M(t), (t), (t) 
T
X x x x , X is the M 1 
output vector measured at receiver, T 
denotes transpose. 
 1 2 D(t), (t), , (t) 
T
S s s s , S is the vector of 
the k arriving signals. 
 1 2 M(t), (t), , (t) 
T
W w w w , W is the noise 
vector: 
 1 1 2 2 D D( , ), ( , ), , (( , )      A a a a , A is 
an MxD “parameter” matrix with 
1 2 i
k k( , ) e ,e , ,e
   
T
j j j
a is a 
“parameter” vector of each signal. 
3. ESTIMATION PROCEDURE 
The multiple signal classification 
algorithm was proposed by R. Schmidt 
[15]. The basic approach of this algorithm 
is that from the received signal, the 
covariance matrix is calculated and then 
eigenvectors decomposition is carried out. 
The signal subspace and noise subspace 
are determined based on eigenvectors and 
eigenvalues. The results showed that the 
M – D dimensional subspace spanned by 
the M – D noise eigenvectors as the noise 
subspace and the D dimensional subspace 
spanned by the incident signal parameter 
vectors as the signal subspace; they are 
disjoint. The signal and the noise 
subspaces are calculated by matrix 
algebra and they are found to be 
orthogonal to each other. Therefore, the 
signal and noise subspaces are isolated by 
the orthogonal property of this algorithm. 
Thus, the complex relative permittivity 
of the material sample is estimated by 
combining the autocorrelation and 
MUSIC function of the received signal. 
The corresponding data covariance matrix 
in equation (7) is given by 
  XXX 2XH HR E XX AS A I (8) 
where XX HS E SS denotes the signal 
covariance matrix, I is the identity matrix, 
H denotes complex conjugate transpose. 
The eigenvalues of XXR are 1 2 D, , ,   
such that: 
 XX i 0det R - λ I = (9) 
Substituting (8) to (9): 
 2X iX ( ) 0Hdet =AS λ IA  (10) 
The eigenvalues i of XX
HAS A are: 
i i
2λ  (11) 
If the eigenvalues i of XX
HAS A are zero, 
XX
HAS A is singular. This means that the 
number of incident wave fronts D is less 
than the number of frequency elements M. 
Thus, The minimum eigenvalue of RXX is 
equivalent to 2 with multiplicity M - D. 
Therefore: 
2
1 2 D D 1 D 2 M       
 (12) 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
34 Số 23 
The eigenvector iu associated with the 
eigenvalue iλ satisfies the following 
equation: 
 XX i i 0R - λ I u = (13) 
For eigenvectors associated with the 
minimum eigenvalue, the (14) is 
suggested by substituting (8) and (12) into 
(13). 
XX i 0
HAS A u = (14) 
Since A has full rank and XXS is non-
singular, thus: 
i
HA u = 0 (15) 
This means that the eigenvectors 
corresponding to the minimum eigenvalue 
are orthogonal to the columns of the 
matrix A. Namely, they are orthogonal to 
the “parameter” vector of the signals: 
  1 1 D DD+1 M , ,a ε ,u ,.. ε a ε ,ε.,u  (16) 
It implies that the squared norm of 
i
HA u is 
zero 
 M Mi 0
H
2
H Ha ε ,ε" U U a ε , =A u = ε" (17)
where  M D 1 D 2 M, ,..., U u u u represents 
the eigenvectors associated with the noise 
subspace of the covariance matrix XXR . 
The pseudo-spectrum of the MUSIC 
function as (18) is given by combining the 
autocorrelation function of signal 
subspace: 
 M
MUSIC
M
, ,
,
, ,
H
H H
a a
P
a UU a
   
 
   
 (18) 
The values of  and  that make MUSICP 
reach a peak that are chosen from the 
result of the estimation. 
4. IMPLEMENTATION MODELING 
In order to make the modeling 
determining the reflection coefficients 
(S11) for the free-space reflection method 
presented in section 2. In this part, we 
have implemented modeling by CST 
software to determine parameter S11 as 
shown in Figure 2. 
Figure 2. Modeling determining the parameters 
(S11) of material sample using CST 
In Figure 2, one pyramidal horn antena is 
designed to operate well in the frequency 
range of 8.0 - 12.0 GHz [16]. The gain 
and voltage standing wave ratio of the 
pyramidal horn antena are 20 dBi and 
1.15 at the center frequency. In this 
model, the distance between the port of 
the antena and the material sample is 
1082.5 mm. Losses due to the spacing of 
the free-space are removed through 
calibration by calculating for an air 
material sample with the same condition. 
The selected material sample is a Teflon-
PTFE nonmagnetic material. The Teflon-
PTFE is widely used in communication 
devices, electronic devices, aerospace, 
and military equipment. In these devices 
and equipment, this material plays a vital 
role in many components, such as power 
divider, combiner, power amplifier, line 
amplifier, base station, RF antena, etc. 
The sample has parameters as follows: the 
Signal input port
Pyramidal horn antenna
Material sample
Metal-Backed
Start
Design of pyramidal horn 
antenna and material sample
S
e
le
c
t 
th
e
 p
a
ra
m
e
te
rs
 a
g
a
in
Stop?
yes
Set up meshes and 
boundaries
Provide signal to antenna 
port at X-band
Start simulation program
Export parameter S11
End
no
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 35 
width and length of the sample are similar 
in size of 150 mm, the complex relative 
permittivity of the sample at 10.0 GHz is 
= 2.1- j0.0002*ε . 
5. RESULTS 
The Teflon-PTFE samples are set up to 
measureat 801 different frequencies from 
8.0 to 12.0 GHz with the scale of 5 MHz. 
From Figure 3 to Figure 7 show the 
pseudo-spectrum for the permittivity of 
Teflon-PTFE samples with the thickness 
of 10 mm, 30 mm, 50 mm, 70 mm, and 
90 mm, respectively. 
Figure 3. Pseudo-spectrum of Teflon-PTFE 
sample at 801 frequencies, frequency range 
of 4.0 GHz and thickness of 10 mm 
Figure 4. Pseudo-spectrum of Teflon-PTFE 
sample at 801 frequencies, frequency range 
of 4.0 GHz and thickness of 30 mm 
Figure 5. Pseudo-spectrum of Teflon-PTFE 
sample at 801 frequencies, frequency range 
of 4.0 GHz and thickness of 50 mm 
Figure 6. Pseudo-spectrum of Teflon-PTFE 
sample at 801 frequencies, frequency range 
of 4.0 GHz and thickness of 70 mm 
Figure 7. Pseudo-spectrum of Teflon-PTFE 
sample at 801 frequencies, frequency range 
of 4.0 GHz and thickness of 90 mm 
Figure 8. The real part of the complex relative 
permittivity of Teflon-PTFE sample is estimated 
by the MUSIS algorithm 
It can be seen from Figures 3, 4, 5, 6, and 
7 that the change in the thickness of the 
sample affects both the sharpness and the 
position of the peak of pseudo-spectrum. 
The change in the position of the peak 
from the expected value means that the 
estimation is not accurate for samples 
with small thickness. Furthermore, the 
drop in the sharpness of the peak makes 
the determination of the point of the 
greatest spectrum more difficult because 
the points around the peak can become 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
36 Số 23 
equal to or greater than the supposed 
peak. These changes combined to create a 
sharp decrease in the accuracy of the 
results as the thickness of the samples 
decreases. 
Figure 9. The imaginary part of the complex 
relative permittivity of Teflon-PTFE sample 
is estimated by the MUSIS algorithm 
Figure 10. Root mean squared error versus 
thickness graph for ε 
Figure 11. Root mean squared error versus 
thickness graph for ε 
The estimation results show that the 
complex relative permittivity of the 
Teflon-PTFE is accurate when the 
thickness changes as Figures 8 and 9. 
Figures 10 and 11 show the root mean 
squared error (RMSE) versus the 
thickness graph calculated from the 
simulation results for the samples at 
different thicknesses. From the results, the 
algorithm can solve for the unique value 
of the permittivity regardless of the 
thickness d but is more accurate with 
samples of larger thickness. The thickness 
of the sample affects the accuracy of the 
measurement of both ε and ε . To get 
the accurate value of the complex relative 
permittivity, the thickness d needs to be 
approximately 50mm or higher. 
6. CONCLUSION 
To propose a super high-resolution 
algorithm to accurately estimate the 
complex relative permittivity of the planar 
material samples using the reflection 
method in free-space. The system consists 
of a pyramidal horn antena and a metal-
backed Teflon-PTFE placed in a free-
space. The parameter vectors of the 
improved MUSIC algorithm describe the 
difference in phase, which indicates the 
difference in frequencies and arrival time 
of the simulated signals. These parameter 
vectors are calculated by using the 
relation between the permittivity and the 
refractive index. The performance of the 
proposed algorithm is verified for all 
scenarios in the simulation. Through the 
results, the ability of the proposed 
algorithm to solve the problem of 
ambiguity of the conventional method is 
also validated. The estimation results of 
the complex relative permittivity using 
proposed algorithm are accurate when the 
thickness of the sample is at least 50 mm. 
The proposed algorithm has great 
benefits in determining the characteristic 
parameters of new materials. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 37 
REFERENCES 
[1] D.K. Ghodgaonkar, V.V. Varadan, and V.K. Varadan, "A free-space method for measurement of 
dielectric constants and loss tangents at microwave frequencies," IEEE Transactions on 
Instrumentation and Measurement, vol. 38, pp. 789-793, 1989. 
[2] Ghodgaonkar. D.K, Varadan. V.V, and Varadan. V.K, "Free-space measurement of complex 
permittivity and complex permeability of magnetic materials at microwave frequencies," 
Instrumentation and Measurement, IEEE Transactions on, vol. 39, pp. 387-394, 1990. 
[3] E. Håkansson, A. Amiet, and A. Kaynak, “Electromagnetic shielding properties of 
polypyrrole/polyester composites in the 1–18GHz frequency range,” Synthetic metals, vol. 156, 
pp. 917-925, 2006. 
[4] V.V. Varadan and R. Ro, “Unique Retrieval of Complex Permittivity and Permeability of Dispersive 
Materials From Reflection and Transmitted Fields by Enforcing Causality,” IEEE Transactions on 
Microwave Theory and Techniques, vol. 55, pp. 2224-2230, 2007. 
[5] V.N. Semenenko and V.A. Chistyaev, “Measurement methods of complex permittivity and 
permeability of sheet samples in free space in microwave range,” In 20th International Crimean 
Conference Microwave & Telecommunication Technology, pp. 1091-1092, 2010. 
[6] J. Roelvink and S. Trabelsi, “Measuring the complex permittivity of thin grain samples by the free-
space transmission technique,” In Instrumentation and Measurement Technology Conference 
(I2MTC), IEEE International, pp. 310-313, 2012. 
[7] R.A. Fenner and S. Keilson, “Free space material characterization using genetic algorithms,” In 
Antena Technology and Applied Electromagnetics (ANTEM), 2014 16th International Symposium 
on, pp. 1-2, 2014. 
[8] K. Haddadi and T. Lasri, “Geometrical Optics-Based Model for Dielectric Constant and Loss 
Tangent Free-Space Measurement,” IEEE Transactions on Instrumentation and Measurement, 
vol. 63, pp. 1818-1823, 2014. 
[9] N.A. Andrushchak, I.D. Karbovnyk, K. Godziszewski, Y. Yashchyshyn, M.V. Lobur, and A.S. 
Andrushchak, “New Interference Technique for Determination of Low Loss Material Permittivity in 
the Extremely High Frequency Range,” IEEE Transactions on Instrumentation and Measurement, 
vol. 64, pp. 3005-3012, 2015. 
[10] T. Tosaka, K. Fujii, K. Fukunaga, and A. Kasamatsu, “Development of Complex Relative 
Permittivity Measurement System Based on Free-Space in 220-330 GHz Range,” IEEE 
Transactions on Terahertz Science and Technology, vol. 5, pp. 102-109, 2015. 
[11] H. Altschuler, “Dielectric constant,” In Handbook of Microwave Measurements, M. Sucher and J. 
Fox, Eds. Brooklyn, NY: Polytechnic Press, Vol. 3, 1963. 
[12] A. Klein, “Microwave moisture determination of coal - A comparison of attenuation and phase 
measuremen,” In Proc. 10th Euro. Microwave Conf., vol. 1, pp. 526–530, 1980. 
[13] P.J. Joseph, J.C. Joseph, D.P. Glynn, III, and T.D. Perkins, III, “A portable vector reflectometer 
and its application for thickness and permittivity measurements,” Microwave J., vol. 2, no. 12, pp. 
84–90, 1994. 
[14] S. Trabelsi, A.W. Kraszewski, and S.O. Nelson, “Phase-shift ambiguity in microwave dielectric 
properties measurements,” IEEE Transactions on Instrumentation and Measurement, vol. 49, pp. 
56–60, 2000. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
38 Số 23 
[15] R. Schmidt, “Multiple emitter location and signal parameter estimation,” IEEE Transactions on 
Antenas and Propagation, vol. 34, pp. 276-280, 1986. 
[16] I.P. Arvind Roy, "Design and Analysis of X band Pyramidal Horn Antena Using HFSS," 
International Journal of Advanced Research in Electronics and Communication Engineering, vol. 
4, pp. 488-493, 2015. 
Biography: 
Ho Manh Cuong was born in Ha Noi, Vietnam, in 1977. He received the Bachelor 
degree in Radio Physics and Electronics at VNU University of Science in 1999 and 
the Master degree in Electronic Engineering at Le Quy Don University in 2006. In 
2019 he received a Ph.D. degree in Electronics Engineering at Le Quy Don 
University. Now, he is a lecturer in Electric Power University, Vietnam. He has 
published many national as well as international papers. His current research 
interests are microwave engineering, antena, electromagnetic theory. 
Le Trong Hieu was born in Hanoi, Vietnam in 1986. He graduated at Le Quy Don 
Technical University in Electronics and Telecommunications, in June 2009. He 
received the M.Sc. and Ph.D. degrees in Electromagnetic Field and Microwave 
Technology from the State Key Laboratory of Millimeter Waves, School of 
Information Science and Engineering, Southeast University, Nanjing, China, in 
2013 and 2018, respectively. Now, he is a lecturer in the Faculty of Electronics 
and Telecommunications, Electric Power University, Hanoi, Vietnam. His fields of 
research are RF/Microwave and Millimeter-waves circuits such as filters, 
amplifiers, antenas for wireless communication applications. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 39