Các bài toán liên quan đến đồ thị hàm số (Có lời giải)
Câu 1: Cho hàm số y=x^3-mx^2+(2m-3)x-1. Tìm m để mọi tiếp tuyến của đồ thị đều có hệ số dương?
Giải
TXĐ: x∈R
Có: y^'=3x^2-2mx+2m-3
Để hàm số có tất cả các hệ số tiếp tuyến dương y^'>0 ,∀m ↔∆^'=m^2-3(2m-3)<0,m (do 3>0)
m^2-6m+9<0 (m-3)^2<0 (vô nghiệm)
Vậy không tồn tại m thoả mãn bài toán

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
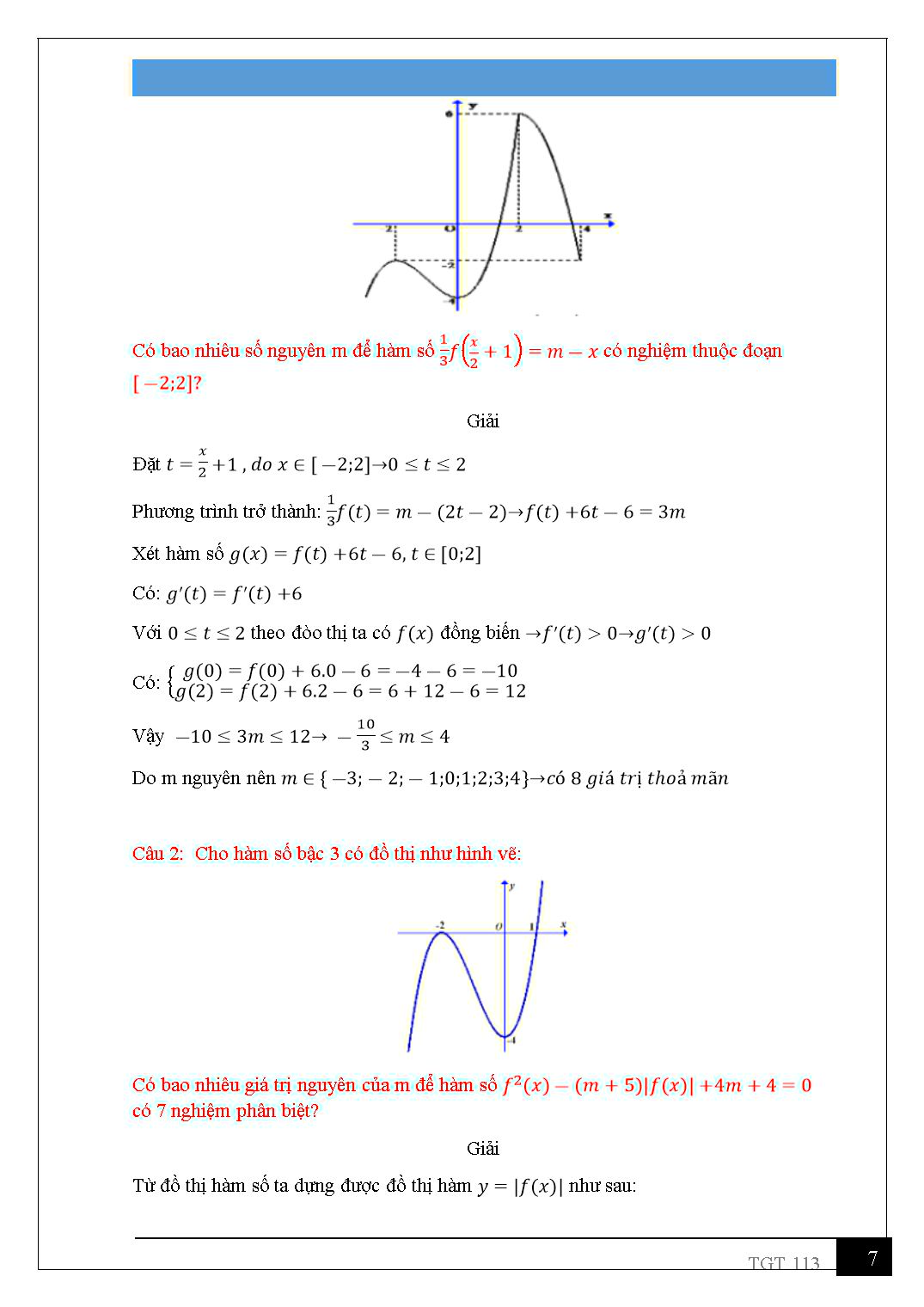
Trang 7

Trang 8
Bạn đang xem tài liệu "Các bài toán liên quan đến đồ thị hàm số (Có lời giải)", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Các bài toán liên quan đến đồ thị hàm số (Có lời giải)

BÀI TOÁN LIÊN QUAN TỚI TIẾP TUYẾN Câu 1: Cho hàm số y=x3-mx2+2m-3x-1. Tìm m để mọi tiếp tuyến của đồ thị đều có hệ số dương? Giải TXĐ: x∈R Có: y'=3x2-2mx+2m-3 Để hàm số có tất cả các hệ số tiếp tuyến dương ó y'>0 , ∀m ↔∆'=m2-32m-30 ó m2-6m+9<0 ó m-32<0 (vô nghiệm) Vậy không tồn tại m thoả mãn bài toán Câu 2: Tìm điểm M có hoành độ âm sao cho tiếp tuyến của hàm số y=13x3-x+23 tại M vuông góc với đường thẳng y=-13x+34? Giải TXĐ: x∈R Có: y'=x2-1 Do tiếp tuyến tại M vuông góc với đường thẳng y=-13x+34 nên y'xM.-13=-1 ó xM2-1=3 ó xM=±2 Do xM Vậy M(-2;0) Câu 3: Tiếp tuyến của hàm số y=-x33+x2+3x-1 có hệ số góc lớn nhất là? Giải TXĐ: x∈R Ta có: y'=-x2+2x+3 Gọi M là điểm có hệ số góc của tiếp tuyến lớn nhất, đặt xM=a Nên, y'M=-a2+2a+3=-a2-2a+1+4=4-a-12≤4 Dấu = xảy ra ó a=2 Vậy hệ số góc lớn nhất là: 4 Câu 4: Tiếp tuyến của đồ thị hàm số y=4x-32x+1 cùng với hai tiệm cận tạo thành tam giác có diện tích là? Thi thử ĐH Chuyên Hùng Vương – Phú Thọ 2019 Giải TXĐ: x∈R/-12 Ta có: y'=102x+12 Gọi Ma,4a-32a+1 là điểm thuộc đồ thị a≠-12 Phương trình tiếp tuyến tại M là: y=10x-a2a+12+4a-32a+1 Tiệm cận TCĐ:x=-12TCN:y=2 Gọi A, B lần lượt là giao điểm của tiếp tuyến tại M với TCĐ và TCN A-12;4a-82a+1B4a+12;2 Giao điểm 2 tiệm cận I-12;2 IA0;-102a+1IB2a+1;0↔IA=102a+1IB=2a+1→S∆IAB=IA.IB2=5 Câu 5: Cho hàm số y=fx có đạo hàm liên tục trên R thoả mãn 2f2x+f1-2x=12x2. Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 là? Thi thử ĐH Chuyên Hà Tĩnh 2019 Giải Tại x=12 có: 2f1+f0=3 Tại x=0: 2f0+f1=0 Nên f0=-1, f1=2 Lại có: 4f'2x-2f'1-2x=24x ó 2f'2x-f'1-2x=12x Tại x=12: 2f'1-f0=6 Tại x=0: 2f'0-f'1=0 Nên f'1=4 Do vậy phương trình tiếp tuyến thoả mãn bài toán là: y=f'1x-1+f1 hay y=4x-2 Chú ý: mấu chốt của phương trình tiếp tuyến là f'x0 và f(x0) do đó ta cần tìm cách để tính được các giá trị đó Câu 6: Cho hàm số y=x3-2021x có đồ thị (C). Gọi M1 là điểm trên (C) có x1=2. Tiếp tuyến của (C) tại M1 cắt đồ thị tại điểm M2 ≠M1. Tiếp tuyến của (C) tại M2 cắt đồ thị tại điểm M3,, tiếp tuyến của (C) tại Mn-1 cắt đồ thị tại điểm Mn (n=4,5). Gọi xn;yn là toạ độ của điểm Mn. Tìm n để 2021xn-yn=22022 Giải Ta có: y'=3x2-2021 Do Mk∈C, nên Mkxk;xk3-2021xk Tiếp tuyến của C tại Mk:(dk) y=3xk2-2021x-xk+xk3-2021xk Phương trình hoành độ giao điểm của dk và (C): x3-2021x=3xk2-2021x-xk+xk3-2021xk ó x-x-k2x+2xk=0 ↔x=xkx=-2xk Vậy Mk+1-2xk; -8xk3+2021.2xk xn+1=-2xn→ xn=2.-2n-1yn=8.-23n-3-2021-2n-1 Vậy 2020xn-yn=22022 ó -13n-3.23n=22022ó n=674 Câu 7: BÀI TOÁN TƯƠNG GIAO ĐỒ THỊ Câu 1: Cho hàm số f(x)=ax3+bx2+cx+d (a,b,c,d ∈R,a≠0) có đồ thị như hình vẽ: Tập nghiệm của phương trình fxfx-4=0 là? Giải Ta có: fxfx-4=0 ó fx=0fx=4 Với fx=0, xét tương giao đồ thị fx với đường thẳng y=0 ta thấy có 2 giao điểm tại x=-1x=2 Với fx=4, xét tương giao đồ thị hàm số f(x) với đường thẳng y=4 ta thấy có 2 giao điểm tại x=0x=3 Vậy phương trình có tập nghiệm S=-1;0;2;4 Câu 2: Cho hàm số bạc 3 có đồ thị như hình vẽ: Số nghiệm thực của phương trình: fx3-3x=1? Giải Ta có: fx3-3x=1 ↔fx3-3x=1fx3-3x=-1 Xét hàm số: gx=x3-3x→g'x=3(x2-1) ó g'x=0 ó x=±1 Bảng biến thiên: x -∞ -1 1 +∞ g'(x) + 0 - 0 + g(x) -∞ 2 -2 +∞ TH1: fx3-3x=1 ó x3-3x=k1 -22→xét tương giao gx có 1 nghiệm TH2: fx3-3x=-1 ó x3-3x=k4 k42→xét tương giao gx có 4 nghiệm Vậy phương trình có tổng 14 nghiệm Câu 3: Cho hàm số y=fx có bảng biến thiên như hình vẽ: Số nghiệm của phương trình fsinx+1=2 trên [-π ; 2π] ? Giải Xét tương giao đồ thị hàm số y=fsinx+1 và đường thẳng y=2 ta được sinx=k1-1 , k12 Do –π≤x≤2π→ -1≤sinx≤1→k4-1>1→sinx=k4-1 vô nghiệmk1-1<-1→sinx=k1-1 vô nghiệm Xét tương giao đò thị hàm số: y=sinx và đường thẳng y=k2-1 và y=k3-1 tại x∈[-π;2π] có 6 giao điểm Vậy phương trình có 6 nghiệm Câu 4: Cho hàm số bậc 4 có đồ thị là đường cong như hình bên. Số nghiệm thực phân biệt của phương trình fx2fx+2=0 là? Câu 49 mã 121 – Thi tốt nghiệp THPT Quốc gia năm 2020 đợt 1 Giải Ta có: fx2fx+2=0 ↔x2fx=0x2fx=k1x2fx=k2x2fx=k3 k1,k2, k3>0 TH1: x2fx=0 ó x2=0→x=0fx=0→có 2 nghiệm TH2: x2fx=k k>0→fx=kx2 Xét hàm số y=kx2, k>0→y'=-2kx3 Bảng biến thiên: x -∞ 0 +∞ y' + || - y 0+∞ || +∞ Vậy đồ thị hàm số y=kx2 cắt đồ thị y=fx tại 2 điểm Vậy tổng 3+2+2+2=9 giao điểm => có 9 nghiệm DẠNG TOÁN BIỆN LUẬN CÓ THAM SỐ Câu 1: Cho hàm số y=fx có đồ thị như hình vẽ: Có bao nhiêu số nguyên m để hàm số 13fx2+1=m-x có nghiệm thuộc đoạn -2;2? Giải Đặt t=x2+1 , do x∈-2;2→0≤t≤2 Phương trình trở thành: 13ft=m-2t-2→ft+6t-6=3m Xét hàm số gx=ft+6t-6, t∈0;2 Có: g't=f't+6 Với 0≤t≤2 theo đòo thị ta có fx đồng biến →f't>0→g't>0 Có: g0=f0+6.0-6=-4-6=-10g2=f2+6.2-6=6+12-6=12 Vậy -10≤3m≤12→ -103≤m≤4 Do m nguyên nên m∈-3;-2;-1;0;1;2;3;4→có 8 giá trị thoả mãn Câu 2: Cho hàm số bậc 3 có đồ thị như hình vẽ: Có bao nhiêu giá trị nguyên của m để hàm số f2x-m+5fx+4m+4=0 có 7 nghiệm phân biệt? Giải Từ đồ thị hàm số ta dựng được đồ thị hàm y=fx như sau: Có: ∆=m+52-44m+4=m2+10m+25-16m-16=m2-6m+9=m-32→ ∆=m-3 Vậy fx=4→có 3 nghiệmfx=m+1 Để phương trình có 7 nghiệm thì phương trình fx=m+1 có 4 nghiệm Từ đồ thị ta được: 0<m+1<4 ó -1<m<3 Do đó có 3 giá trị nguyên của m Câu 3: Tìm giá trị thực của tham số m để đường thẳng d:y=x-m+2 cắt đồ thị hàm số y=2xx-1 C tại hai điểm A, B sao cho AB ngắn nhất? Giải TXĐ: x∈R/1 Phương trình hoành độ giao điểm: 2xx-1=x-m+2 ó fx=x2-m+1x+m-2 1 Để (d) và (C) cắt nhau tại 2 điểm phân biệt ó ∆=m+12-4m-2=m2-2m+9>0f1=1-m+1+m-2≠0 luôn đúng với ∀m∈TXĐ Đặt Ax1;x1-m+2Bx2;x2-m+2→với ∀m ta luôn có:x1+x2=m+1x1x2=m-2 AB2=x2-x12+x2-m+2-x1+m-22=2x2-x12=2x1+x22-2x1x22=2m+12-2m-22=2m-12+8≥16 Vậy ABmin=4 ó m=1 Câu 4: Cho hai ha
File đính kèm:
 cac_bai_toan_lien_quan_den_do_thi_ham_so_co_loi_giai.docx
cac_bai_toan_lien_quan_den_do_thi_ham_so_co_loi_giai.docx

