Bài giảng Xử lý tín hiệu số - Chương 6: Transfer functions and digital filter realization - Hà Hoàng Kha
Content
1 T . Transf f er functions
Impulse response
Difference equation
Impulse response
Frequency response
2 Digital filter realization
Block diagram of realization
.
Direct form
Canonical form
Cascade form
3 Transfer functions
and Digital Filter Realizations
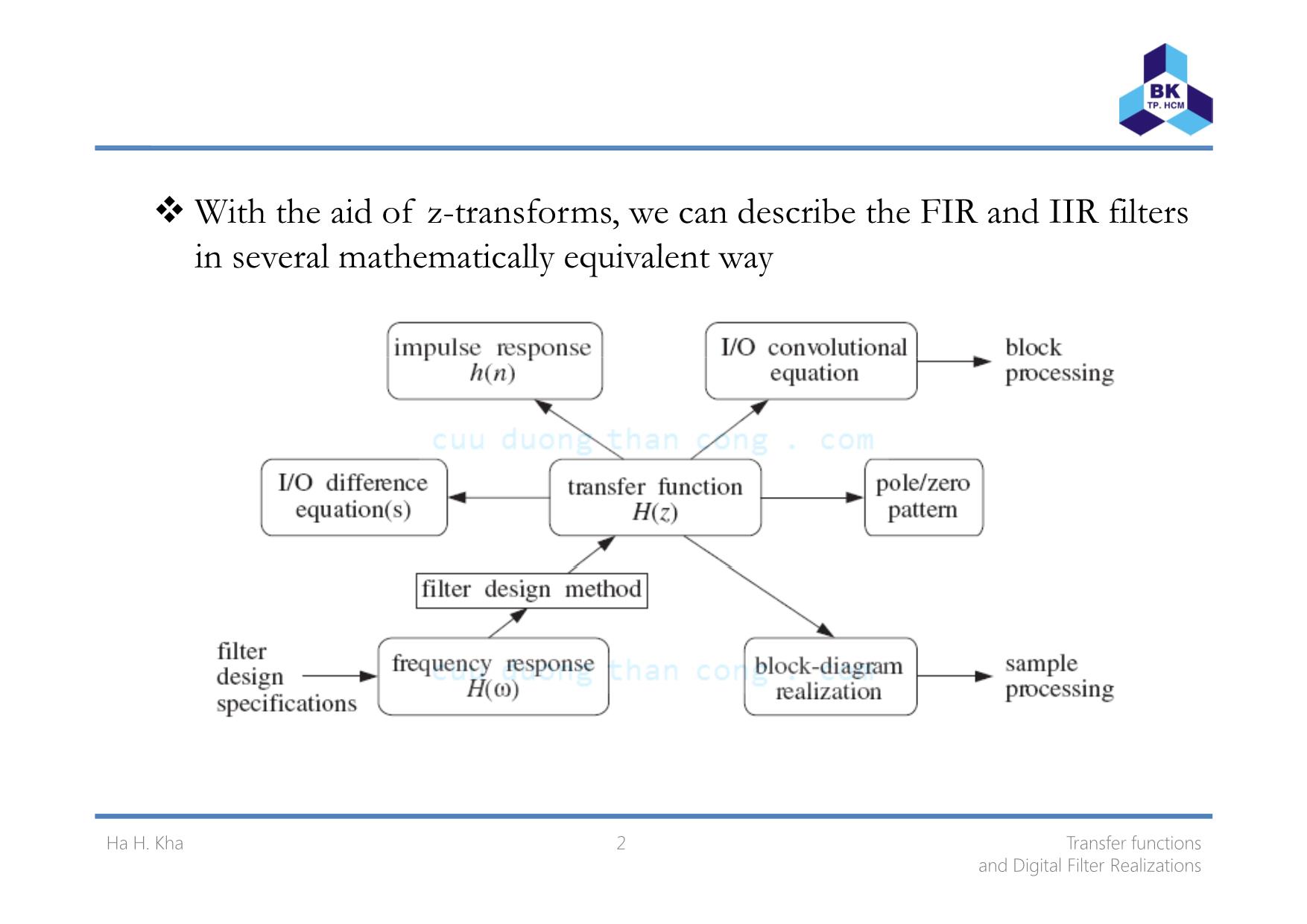
Given a transfer functions H(z) one can obtain:
( ) th i a) the impulse response h( ) n)
(b) the difference equation satisfied the impulse response
( ) h c) the I/O difference equation rel i ating the output y( ) n) to th i e input
x(n).
(d) the block diagram realization of the filter
( ) e) the sample-by-samp p le processing g algorithm
(f) the pole/zero pattern
(g) the frequency response H( )

Trang 1
Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Xử lý tín hiệu số - Chương 6: Transfer functions and digital filter realization - Hà Hoàng Kha

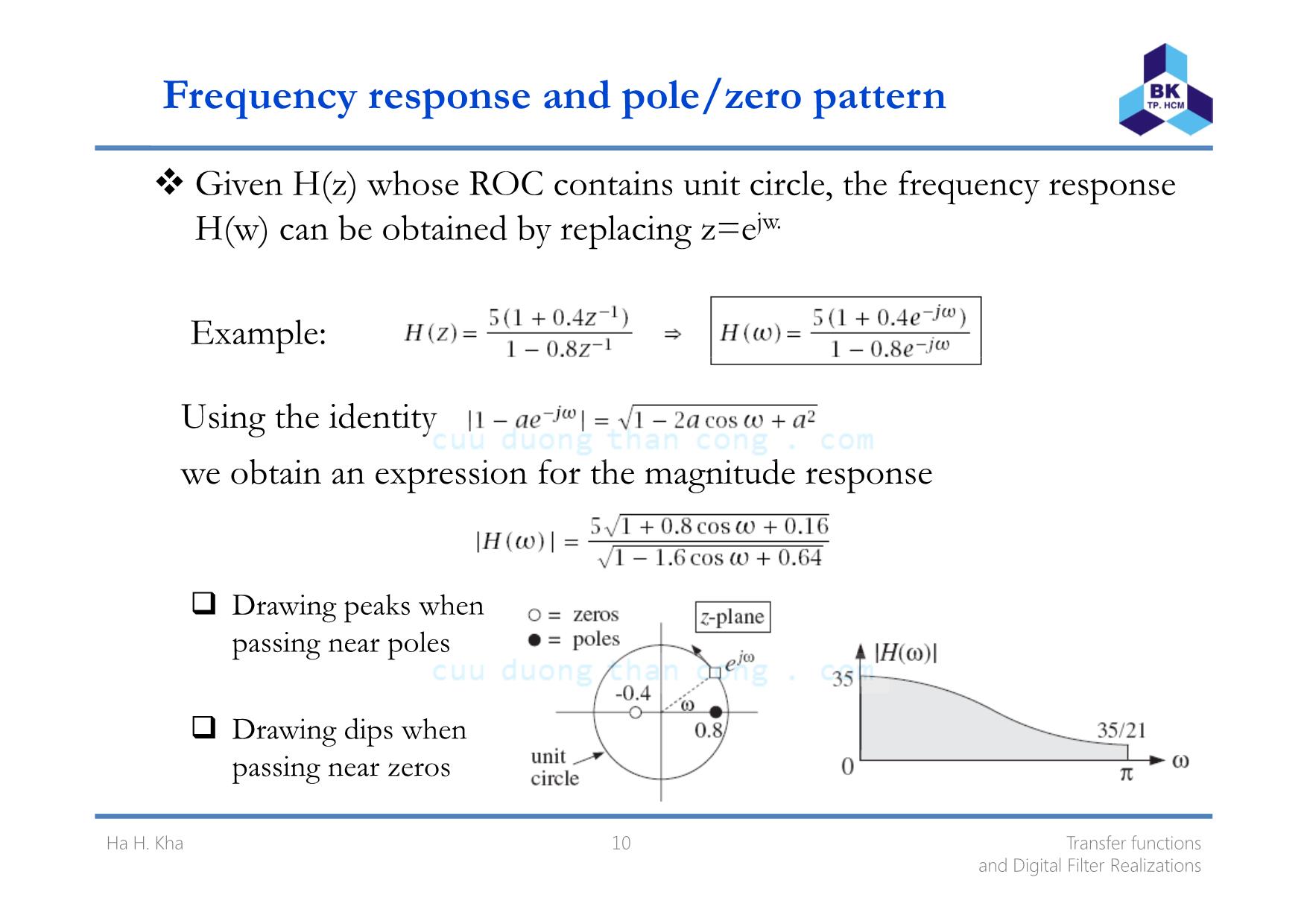
Chapter 6 Transfer functions and Digital Filter Realization Click to edit Master subtitle styleHa Hoang Kha, Ph.D. Ho Chi Minh City University of Technology Email: hhkha@hcmut.edu.vn cn tt With the aid of z-transforms, we can describe the FIR and IIR filters in se eral mathematicall eq i alent a v y u v w y Ha H. Kha 2 Transfer functions and Digital Filter Realizations cn tt Content 1 T f f ti. rans er unc ons Impulse response Difference equation Impulse response Frequency response 2 Digital filter realization Block diagram of realization . Direct form Canonical form Cascade form 3 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt 1. Transfer functions Given a transfer functions H(z) one can obtain: ( ) th i l h( )a e mpu se response n (b) the difference equation satisfied the impulse response ( ) h / diff i l i h ( ) h ic t e I O erence equat on re at ng t e output y n to t e nput x(n). (d) the block diagram realization of the filter (e) the sample-by-sample processing algorithm (f) the pole/zero pattern (g) the frequency response H(w) 4 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Impulse response Taking the inverse z-transform of H(z) yields the impulse response h(n) Example: consider the transfer function To obtain the impulse response, we use partial fraction expansion to write Assuming the filter is causal, we find 5 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Difference equation for impulse response The standard approach is to eliminate the denominator polynomial of H(z) and then transfer back to the time domain. Example: consider the transfer function Multiplying both sides by denominator, we find Taking inverse z transform of both sides and using the linearity and - delay properties, we obtain the difference equation for h(n): 6 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt I/O difference equation Write then eliminate the denominators and go back to the time domain. Example: consider the transfer function We have which can write Taking the inverse z-transforms of both sides, we have Thus, the I/O difference equation is 7 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Block diagram One the I/O difference equation is determined, one can mechanize it by block diagram Example: consider the transfer function We have the I/O difference equation The direct form realization is given by 8 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Sample processing algorithm From the block diagram, we assign internal state variables to all the delays: We define v1(n) to be the content of the x-delay at time n: Similarly, w1(n) is the content of the y-delay at time n: 9 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Frequency response and pole/zero pattern Given H(z) whose ROC contains unit circle, the frequency response H(w) can be obtained by replacing z=ejw. Example: Using the identity b i i f h i dwe o ta n an express on or t e magn tu e response Drawing peaks when passing near poles Drawing dips when passing near zeros 10 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Example Consider the system which has the I/O equation: a) Determine the transfer function b) Determine the casual impulse response c) Determine the frequency response and plot the magnitude response of the filter. d) Plot the block diagram of the system and write the sample processing algorithm 11 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt 2. Digital filter realizations Construction of block diagram of the filter is called a realization of the filter . Realization of a filter at a block diagram level is essentially a flow graph of the signals in the filter. It includes operations: delays, additions and multiplications of signals by a constant coefficients. The block diagram realization of a transfer function is not unique. Note that for implementation of filter we must concerns the accuracy of signal values, accuracy of coefficients and accuracy of arithmetic operations. We must analyze the effect of such imperfections on the performance of the filter. 12 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Direct form realization Use the I/O difference equation The b-multipliers are feeding forward The a-multipliers are feeding backward 13 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Example Consider IIR filter with h(n)=0.5nu(n) ) D th di t f li ti f thi di it l filt ?a raw e rec orm rea za on o s g a er b) Given x=[2, 8, 4], find the first 6 samples of the output by using the sample processing algorithm ? 14 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Canonical form realization Note that )( )( 1)()()()( zX zD zNzXzHzY == The maximum number of common delays: K=max(L,M) 15 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Cascade form The cascade realization form of a general functions assumes that the transfer functions is the product of such second-order sections (SOS): Each of SOS may be realized in direct or canonical form. 16 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Cascade form 17 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt Homework Problems: 6.1, 6.2, 6.5, 6.16, 6.18, 6.19 Problems: 7.1, 7.3, 7.5, 7.10 18 Transfer functions and Digital Filter Realizations Ha H. Kha cn tt
File đính kèm:
 bai_giang_xu_ly_tin_hieu_so_chuong_6_transfer_functions_and.pdf
bai_giang_xu_ly_tin_hieu_so_chuong_6_transfer_functions_and.pdf

