Bài giảng Xử lý tín hiệu số - Chương 5: z-Transform - Hà Hoàng Kha

Chapter 5
z-Transform
Click to edit Master subtitle styleHa Hoang Kha, Ph.D.
Ho Chi Minh City University of Technology
Email: hhkha@hcmut.edu.vn
™ The z-transform is a tool for analysis, design and implementation of 
discrete time signals and LTI systems- .
™ Convolution in time-domain ⇔ multiplication in the z-domain
Ha H. Kha 2 z-Transforms
Content
1 t f. z- rans orm
2. Properties of the z-transform
3. Causality and Stability
4. Inverse z-transform
3 Discrete-Time SystemsHa H. Kha
1. The z-transform
™ The z-transform of a discrete-time signal x(n) is defined as the power 
series:
"" ++++−+−== −−−
∞
−∞=
−∑ 212 )2()1()0()1()2()()( zxzxxzxzxznxzX
n
n
™ The region of convergence (ROC) of X(z) is the set of all values of 
f hi h X( ) i fi i lz or w c z atta ns a n te va ue.
})()(|C{ ∑∞ − ∞≠=∈= nznxzXzROC
−∞=n
™ The z-transform of impulse response h(n) is called the transform 
function of the filter: 
∑∞
∞
−=
n
nznhzH )()(
4 z-Transforms
−=
Ha H. Kha
Example
™ Determine the z-transform of the following finite-duration signals
a) x1(n)=[1, 2, 5, 7, 0, 1]
b) x2(n)=x1(n-2)
c) x3(n)=x1(n+2)
d) x4(n)=δ(n)
e) x (n)=δ(n k) k>0 5 - , 
f) x6(n)=δ(n+k), k>0
5 z-TransformsHa H. Kha
Example
™ Determine the z-transform of the signal
) ( )=(0 5)n ( )a x n . u n
b) x(n)=-(0.5)nu(-n-1)
6 z-TransformsHa H. Kha
z-transform and ROC
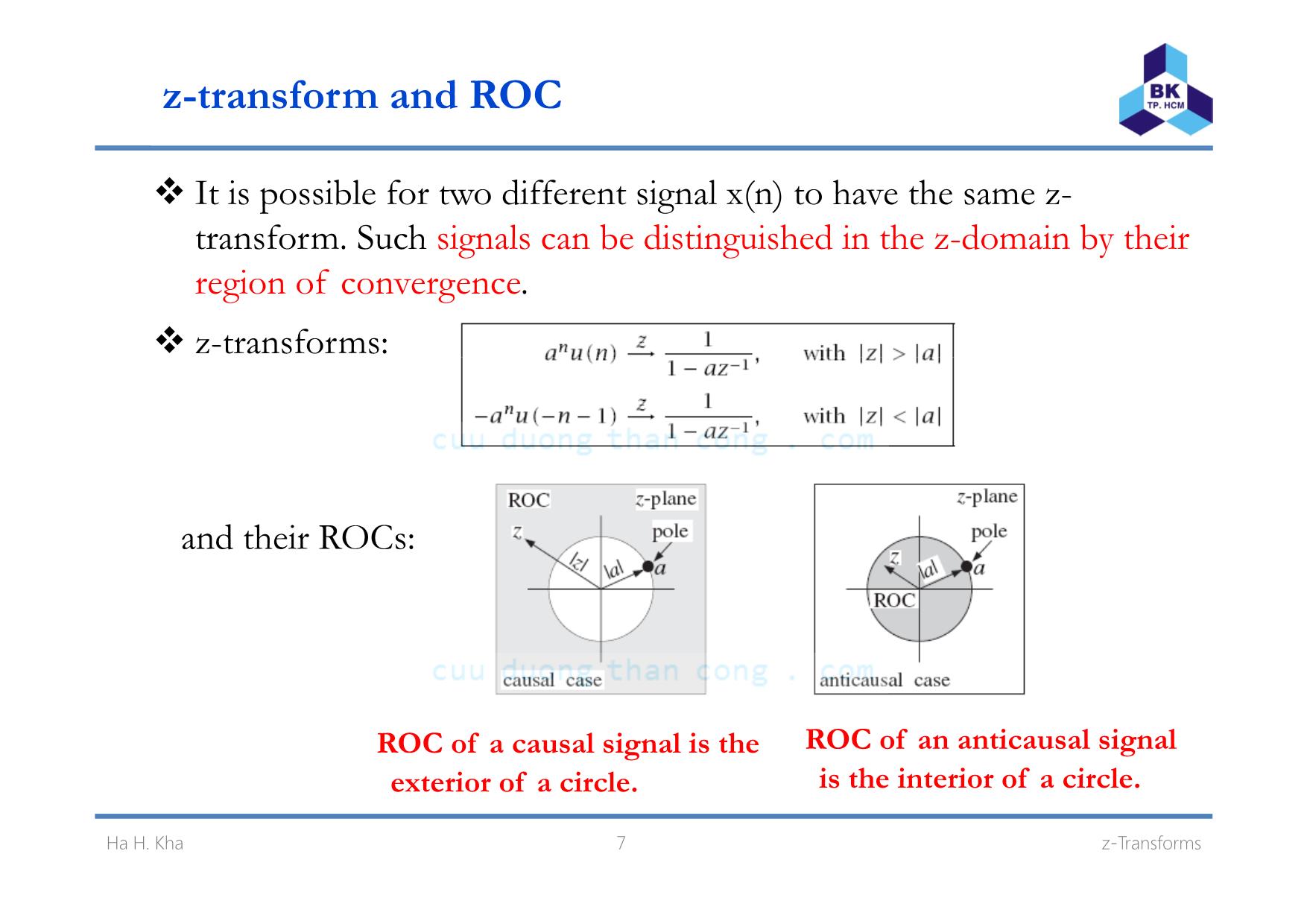
™ It is possible for two different signal x(n) to have the same z-
transform. Such signals can be distinguished in the z-domain by their 
region of convergence.
™ z-transforms:
and their ROCs:
ROC of a causal signal is the 
t i f i l
ROC of an anticausal signal 
is the interior of a circle
7 z-Transforms
ex er or o a c rc e. .
Ha H. Kha
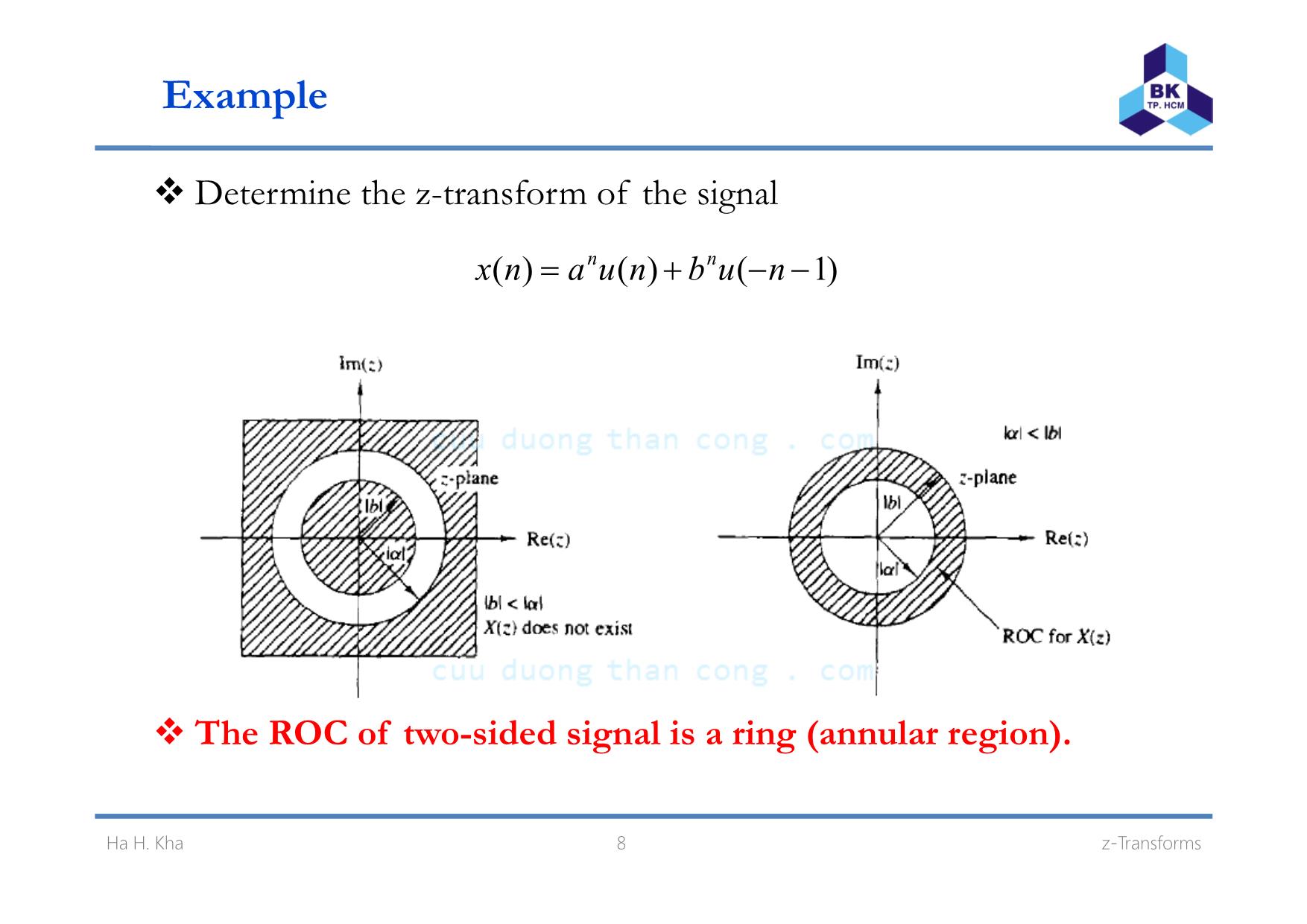
Example
™ Determine the z-transform of the signal
)1()()( −−+= nubnuanx nn
™ The ROC of two-sided signal is a ring (annular region).
8 z-TransformsHa H. Kha
2. Properties of the z-transform
™ Linearity:
111 ROCwith)()( zXnx
z⎯→←if
222 ROCwith)()( zXnx
z⎯→←and
then 
212121 ROCROCROCwith)()()()()()( ∩=+=⎯→←+= zXzXzXnxnxnx z
™ Example: Determine the z-transform and ROC of the signals
a) x(n)=[3(2)n-4(3)n]u(n)
b) x(n)=cos(w0 t)u(n)
c) x(n)=sin(w0 t)u(n)
9 z-TransformsHa H. Kha
2. Properties of the z-transform
™ Time shifting:
)()( zXnx z⎯→←if
)()( zXzDnx Dz −⎯→←−then 
™ The ROC of is the same as that of X(z) except for z=0 if)(zXz D− 
D>0 and z=∞ if D<0.
Example: Determine the z transform of the signal x(n)=2nu(n 1) - - .
™ Scaling in the z-domain:
21 || :ROC)()( rzrzXnx
z ≤≤⎯→←if
21
1 ||||||:ROC)()( razrazaXnxa zn ≤≤⎯→← −then 
for any constant a, real or complex
Example: Determine the z-transform of the signal x(n)=ancos(w0n)u(n)
10 z-Transforms
 .
Ha H. Kha
2. Properties of the z-transform
™ Time reversal:
if 21 || :ROC)()( rzrzXnx z ≤≤⎯→←
then 
12
1 1||
r
1 :ROC)()(
r
zzXnx z ≤≤⎯→←− −
Example: Determine the z-transform of the signal x(n)=u(-n).
™ Convolution of two sequence:
if and )()( 11 zXnx z⎯→← )()( 22 zXnx z⎯→←
)()()()()()( 2121 zXzXzXnxnxnx
z =⎯→←∗=then 
the ROC is, at least, the intersection of that for X1(z) and X2(z).
Example: Compute the convolution of x=[1 1 3 0 2 1] and h=[1, -2, 1] ?
11 z-TransformsHa H. Kha
2. Properties of the z-transform
™Differentiation in the z-domain
if )()( zXnx z⎯→←
then 
dz
zdXznnx z )()( −⎯→←
Example: Determine the z transform of the signal x(n)=nanu(n)
the ROCs of both are the same.
 - .
12 z-TransformsHa H. Kha
3. Causality and stability
™ A causal signal of the form
"++= )()()( nupAnupAnx nn
will have z-transform
2211
||max||ROC)( 21 AAX >++
11 12
1
1
ii
pz
zpzp
z −−= −− "
the ROC of causal signals are outside of the circle.
™ A anticausal signal of the form
"+−−−−−−= )1()1()( 2211 nupAnupAnx nn
||min||ROC)( 21 ipz
AAzX <++= "
11 12
1
1
izpzp −− −−
the ROC of causal signals are inside of the circle.
13 z-TransformsHa H. Kha
3. Causality and stability
™Mixed signals have ROCs that are the annular region between two 
circles.
™ It can be shown that a necessary and sufficient condition for the 
stability of a signal x(n) is that its ROC contains the unit circle. 
14 z-TransformsHa H. Kha
4. Inverse z-transform
ROC ),()( transformz zXnx ⎯⎯⎯ →⎯ −
)(ROC ),( transform-zinverse nxzX ⎯⎯⎯⎯⎯ →⎯
ROC),()( zXnx z⎯→←
™ In inverting a z-transform, it is convenient to break it into its partial 
fraction (PF) expression form, i.e., into a sum of individual pole 
terms whose inverse z transforms are known.
1™ Note that with we have 
⎧ > i l )( l||||ROCif)(n
1-az-1
)( =zX
⎩⎨ <−−−
=
signals) l(anticausa |a||z| ROC if )1(
s gna scausa az
)(
nua
nua
nx n
15 z-TransformsHa H. Kha
Partial fraction expression method
™ In general, the z-transform is of the form
N
N zbzbbzNzX
−− +++== "
1
10)()(
™ The poles are defined as the solutions of D(z)=0. There will be M 
poles say at p p p Then we can write
M
M zazazD
−− ++ "101)(
, 1, 2,, M . , 
)1()1)(1()( 112
1
1
−−− −−−= zpzpzpzD M"
™ If N < M and all M poles are single poles.
where
16 z-TransformsHa H. Kha
Exampleod
™ Compute all possible inverse z-transform of 
Solution:
- Find the poles: 1-0.25z-2 =0 Æ p1=0.5, p2=-0.5
- We have N=1 and M=2, i.e., N < M. Thus, we can write 
where
17 z-TransformsHa H. Kha
Exampleod
18 z-TransformsHa H. Kha
Partial fraction expression method
™ If N=M
Wh d f i 1 Mere an or = ,,
™ If N> M
19 z-TransformsHa H. Kha
Exampleod
™ Compute all possible inverse z-transform of 
Solution:
- Find the poles: 1-0.25z-2 =0 Æ p1=0.5, p2=-0.5
- We have N=2 and M=2, i.e., N = M. Thus, we can write 
where
20 z-TransformsHa H. Kha
Exampleod
21 z-TransformsHa H. Kha
Exampleod
™ Determine the causal inverse z-transform of
Solution:
h 5 d 2 i Th h di id h- We ave N= an M= , .e., N > M. us, we ave to v e t e 
denominator into the numerator, giving
22 z-TransformsHa H. Kha
Partial fraction expression method
™ Complex-valued poles: since D(z) have real-valued coefficients, the 
complex-valued poles of X(z) must come in complex-conjugate pairs 
C id i h l hons er ng t e causa case, we ave 
Writing A1 and p1 in their polar form, say, 
with B1 and R1 > 0, and thus, we have 
A lt th i l i ti d i is a resu , e s gna n me- oma n s 
23 z-TransformsHa H. Kha
Exampleod
™ Determine the causal inverse z-transform of
Solution:
24 z-TransformsHa H. Kha
Exampleod
25 z-TransformsHa H. Kha
Homework
™ Problems: 5.2, 5.3, 5.4, 5.6, 5.6, 5.8, 5.16
26 z-TransformsHa H. Kha