Bài giảng Xử lý tín hiệu số - Chương 4: Thiết kế bộ lọc số - Đặng Quang Hiếu

ET4020 - Xử lý tín hiệu số
Chương 4: Thiết kế bộ lọc số
TS. Đặng Quang Hiếu
Trường Đại học Bách Khoa Hà Nội
Viện Điện tử - Viễn thông
Năm học 2012 - 2013
Outline
Tổng quan
Thiết kế bộ lọc FIR
Thiết kế bộ lọc IIR
Thiết kế bộ lọc chọn lọc tần số
|H(ejω)|
ω
1 + δ1
1− δ1
δ2
ωp ωs0 pi
Các chỉ tiêu kỹ thuật:
◮ Tần số cắt (ωc), và dải chuyển tiếp (ωp, ωs)
◮ Độ gợn sóng dải thông δ1
◮ Độ gợn sóng dải chắn δ2
Qui trình
(1) Specifications: Xác định các chỉ tiêu kỹ thuật dựa trên ứng
dụng thực tế.
(2) Approximation: Tổng hợp hệ thống LTI có chỉ tiêu xấp xỉ với
yêu cầu đặt ra.
(3) Realization: Thực hiện hệ thống dựa trên các công cụ phần
cứng / phần mềm hiện có.
Khóa học này chỉ nghiên cứu #2: Tìm các tham số ak , br ,M,N
sao cho đáp ứng tần số H(ejω) của hệ thống LTI dưới đây có các
thông số xấp xỉ với các chỉ tiêu kỹ thuật mong muốn ωs , ωp, δ1, δ2.
y(n) = −
N∑
k=1
aky(n − k) +
M−1∑
r=0
brx(n − r)
Phân loại bộ lọc số
Có thể thực hiện được trên thực tế:
◮ Hệ thống LTI
◮ Nhân quả
◮ Ổn định
Phân loại theo chiều dài đáp ứng xung:
◮ Bộ lọc FIR
◮ Bộ lọc IIR
Phân loại theo cách thiết kế:
◮ Sử dụng các công thức
◮ Mang tính giải thuật (vòng lặp)
Outline
Tổng quan
Thiết kế bộ lọc FIR
Thiết kế bộ lọc IIR
Bộ lọc có đáp ứng xung chiều dài hữu hạn
y(n) =
M∑
r=0
brx(n − r)
→ h(n) =
{
bn, 0 ≤ n ≤ (M − 1)
0, n còn lại
Ưu điểm của bộ lọc FIR:
◮ Luôn ổn định
◮ Có thể thực hiện với hiệu năng cao (sử dụng FFT)
◮ Dễ tổng hợp bộ lọc pha tuyến tính
Khái niệm pha tuyến tính
Tại sao pha tuyến tính?
◮ Trễ nhóm không đổi
◮ Độ phức tạp tính toán giảm
Khi nào pha tuyến tính?
(i) h(n) đối xứng: h(n) = h(M − 1− n)
(ii) h(n) phản đối xứng: h(n) = −h(M − 1− n) và h (M−12 ) = 0
với M lẻ.
Phân loại bộ lọc pha tuyến tính
M lẻ M chẵn
h(n) đối xứng loại 1 loại 2
h(n) phản đối xứng loại 3 loại 4
H1(e
jω) = e−jω
M−1
2
h(M − 1
2
)
+ 2
M−3
2∑
n=0
h(n) cosω
(
M − 1
2
− n
)
H2(e
jω) = e−jω
M−1
2 · 2
M
2
−1∑
n=0
h(n) cosω
(
M − 1
2
− n
)
H3(e
jω) = e−j [ω
M−1
2
+pi
2
] · 2
M−3
2∑
n=0
h(n) sinω
(
M − 1
2
− n
)
H4(e
jω) = e−j [ω
M−1
2
+pi
2
] · 2
M
2
−1∑
n=0
h(n) sinω
(
M − 1
2
− n
)
Vị trí các điểm không
◮ Khi h(n) đối xứng / phản đối xứng, dễ dàng chứng minh được:
H(z) = ±z−(M−1)H(z−1)
◮ Nếu H(z) có nghiệm z1 thì cũng có các nghiệm sau:
z∗1 , 1/z1, 1/z
∗
1
◮ Biểu diễn vị trí các điểm không trên mặt phẳng phức?
Phương pháp cửa sổ - Khái niệm
Giả sử cần thiết kế bộ lọc có đáp ứng tần số mong muốn Hd (e
jω)
thỏa mãn các chỉ tiêu kỹ thuật. Khi đó:
hd(n) =
1
2pi
∫ pi
−pi
Hd (e
jω)ejωndω
Tuy nhiên, trong trường hợp lý tưởng, hd(n) có chiều dài vô hạn
và không nhân quả → dịch đi (M − 1)/2 mẫu và nhân với hàm
cửa sổ w(n)
h(n) = hd(n − M − 1
2
) · w(n)
trong đó
w(n) = 0,∀n (M − 1)
Phương pháp cửa sổ - Các bước thiết kế
(1) Cho các chỉ tiêu kỹ thuật : δ1, δ2, ωp, ωs
(2) Chọn loại cửa sổ và tính w(n) với chiều dài M, tâm đối xứng
tại (M − 1)/2.
(3) Tính các hệ số hd(n) của bộ lọc lý tưởng, sau đó tính các hệ
số h(n) nhờ trễ và nhân với hàm cửa sổ w(n).
(4) So sánh H(ejω) với các chỉ tiêu kỹ thuật. Nếu không thỏa mãn
thì tăng M và quay lại bước (2).
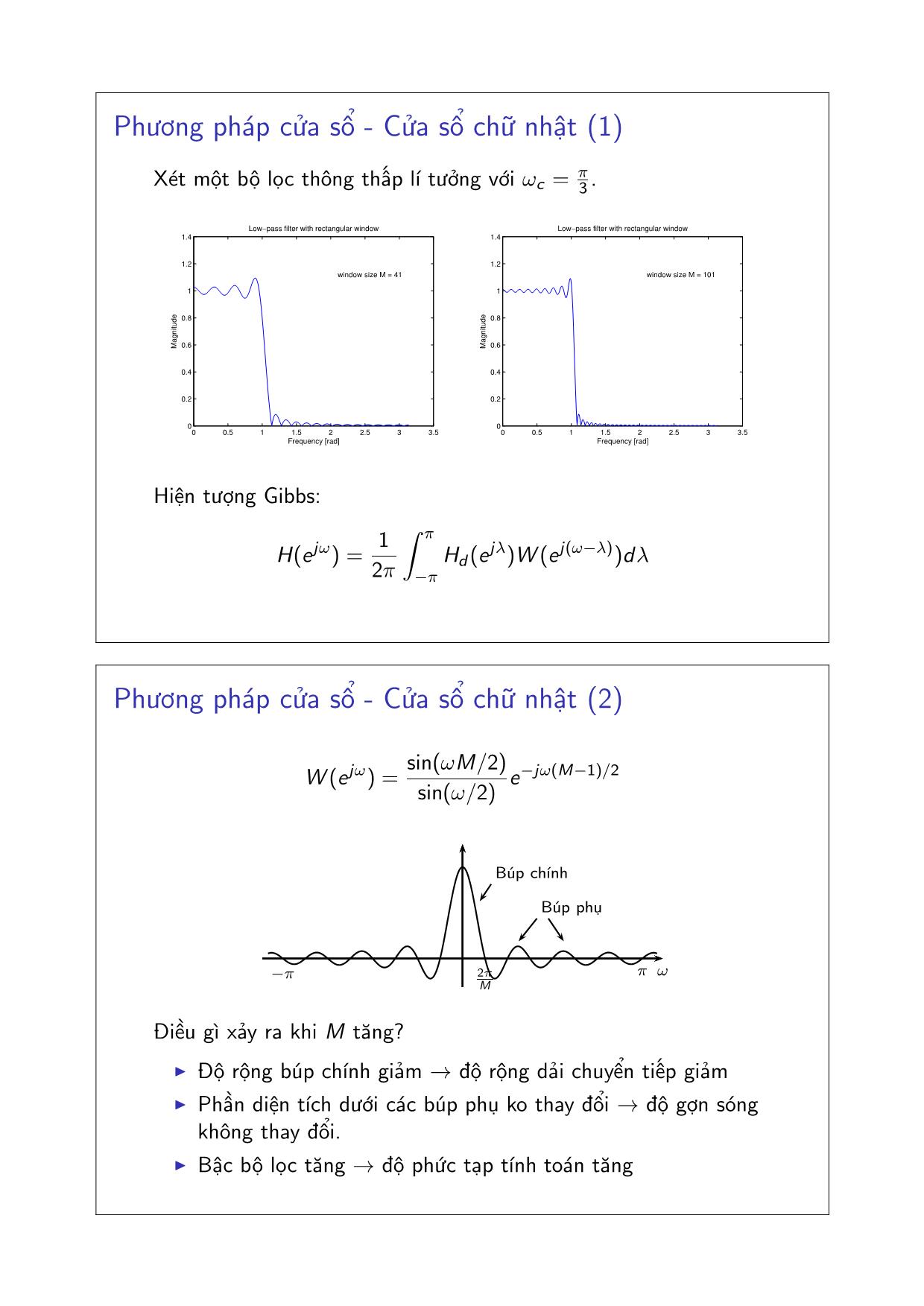
Phương pháp cửa sổ - Cửa sổ chữ nhật (1)
Xét một bộ lọc thông thấp lí tưởng với ωc =
pi
3 .
0 0.5 1 1.5 2 2.5 3 3.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Low−pass filter with rectangular window
window size M = 41
Frequency [rad]
M
ag
ni
tu
de
0 0.5 1 1.5 2 2.5 3 3.5
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Low−pass filter with rectangular window
window size M = 101
Frequency [rad]
M
ag
ni
tu
de
Hiện tượng Gibbs:
H(ejω) =
1
2pi
∫ pi
−pi
Hd (e
jλ)W (ej(ω−λ))dλ
Phương pháp cửa sổ - Cửa sổ chữ nhật (2)
W (ejω) =
sin(ωM/2)
sin(ω/2)
e−jω(M−1)/2
ω2pi
M
pi−pi
Búp chính
Búp phụ
Điều gì xảy ra khi M tăng?
◮ Độ rộng búp chính giảm → độ rộng dải chuyển tiếp giảm
◮ Phần diện tích dưới các búp phụ ko thay đổi → độ gợn sóng
không thay đổi.
◮ Bậc bộ lọc tăng → độ phức tạp tính toán tăng
Phương pháp cửa sổ - Giải pháp
◮ Chọn loại cửa sổ thay đổi mềm hơn trên miền thời gian → các
búp phụ thấp hơn.
◮ Khi đó, dải chuyển tiếp rộng hơn.
◮ Tăng bậc của bộ lọc nhằm giảm độ rộng dải chuyển tiếp.
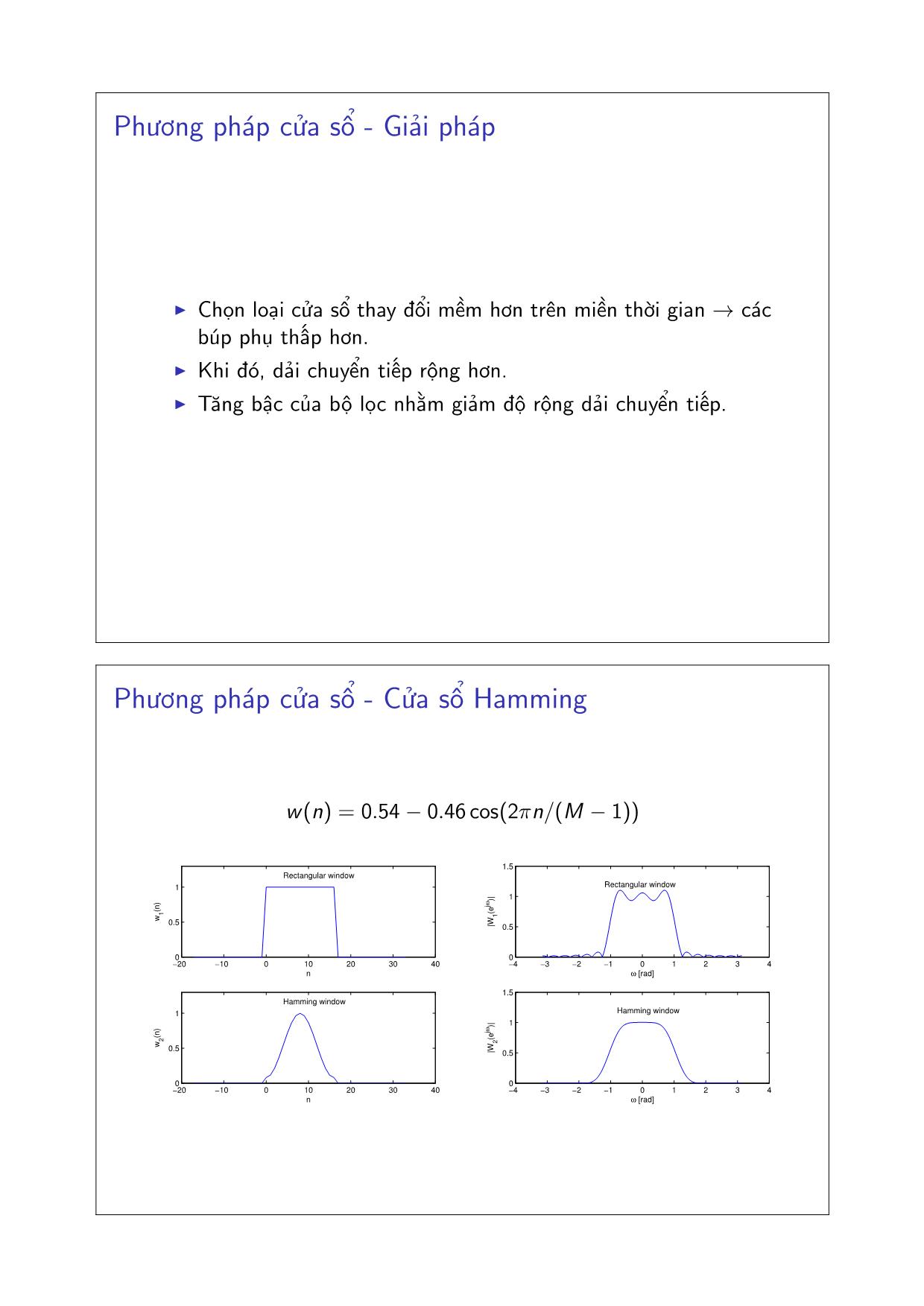
Phương pháp cửa sổ - Cửa sổ Hamming
w(n) = 0.54 − 0.46 cos(2pin/(M − 1))
−20 −10 0 10 20 30 40
0
0.5
1
Rectangular window
n
w
1(n
)
−4 −3 −2 −1 0 1 2 3 4
0
0.5
1
1.5
Rectangular window
ω [rad]
|W
1(e
jω )
|
−20 −10 0 10 20 30 40
0
0.5
1
Hamming window
n
w
2(n
)
−4 −3 −2 −1 0 1 2 3 4
0
0.5
1
1.5
Hamming window
ω [rad]
|W
2(e
jω )
|
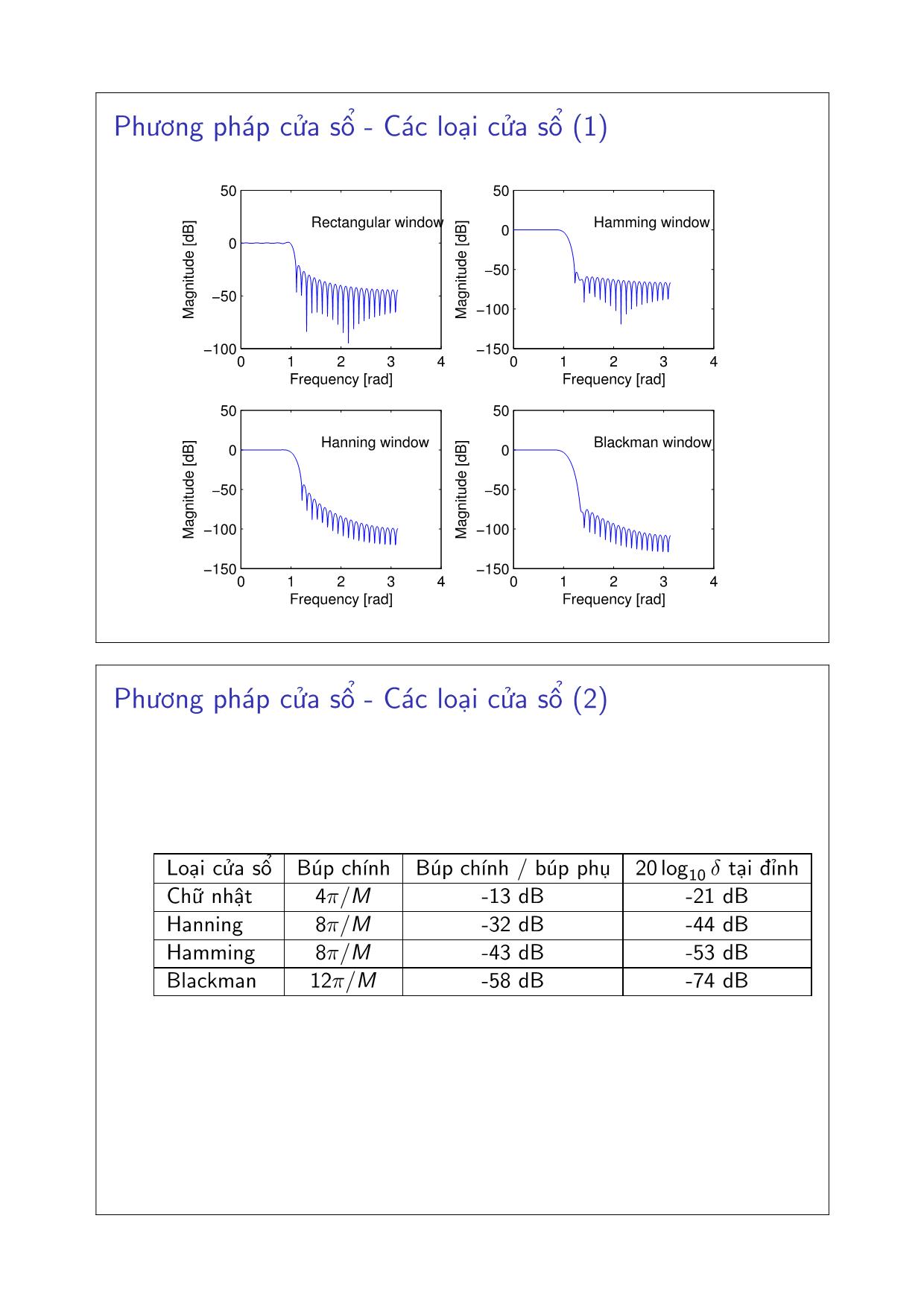
Phương pháp cửa sổ - Các loại cửa sổ (1)
0 1 2 3 4
−100
−50
0
50
Rectangular window
Frequency [rad]
M
ag
ni
tu
de
 [d
B]
0 1 2 3 4
−150
−100
−50
0
50
Hamming window
Frequency [rad]
M
ag
ni
tu
de
 [d
B]
0 1 2 3 4
−150
−100
−50
0
50
Hanning window
Frequency [rad]
M
ag
ni
tu
de
 [d
B]
0 1 2 3 4
−150
−100
−50
0
50
Blackman window
Frequency [rad]
M
ag
ni
tu
de
 [d
B]
Phương pháp cửa sổ - Các loại cửa sổ (2)
Loại cửa sổ Búp chính Búp chính / búp phụ 20 log10 δ tại đỉnh
Chữ nhật 4pi/M -13 dB -21 dB
Hanning 8pi/M -32 dB -44 dB
Hamming 8pi/M -43 dB -53 dB
Blackman 12pi/M -58 dB -74 dB
Phương pháp cửa sổ - Thiết kế
Một số điểm cần lưu ý khi thiết kế
◮ Tần số cắt nằm giữa dải chuyển tiếp
◮ Độ gợn sóng dải thông và dải chắn xấp xỉ bằng nhau. Thường
được tính đơn vị dB (20 log10(δ)).
◮ Độ rộng dải chuyển tiếp nhỏ hơn độ rộng búp chính.
◮ Khoảng cách giữa 2 đỉnh ở hai đầu dải chuyển tiếp xấp xỉ
bằng độ rộng búp chính.
Các phương pháp khác
◮ Lấy mẫu tần số
◮ Các phương pháp lặp
Tự học!
Bài về nhà
(1) Vẽ phổ bộ lọc pha tuyến các loại (1,2,3,4) và nhận xét?
(2) Vẽ dạng cửa sổ (trên miền thời gian), và phổ bộ lọc thông
thấp lý tưởng sử dụng các loại cửa sổ trên? So sánh?
(3) Vẽ phổ bộ lọc được thiết kế sử dụng phương pháp lấy mẫu tần
số cho các loại?
(4) Viết chương trình thiết kế bộ lọc bằng phương pháp lặp?
Outline
Tổng quan
Thiết kế bộ lọc FIR
Thiết kế bộ lọc IIR
Bộ lọc IIR
y(n) = −
N∑
k=1
aky(n − k) +
M∑
r=0
brx(n − r)
Hàm truyền đạt:
H(z) =
∑M
r=0 brz
−r
1+
∑N
k=1 akz
−k
So sánh với bộ lọc FIR:
◮ Khi không cần có pha tuyến tính, bộ lọc IIR có độ phức tạp
tính toán thấp hơn (với cùng chỉ tiêu kỹ thuật).
◮ Khó thiết kế
◮ Phải đảm bảo tính ổn định của hệ thống
Tổng hợp bộ lọc IIR từ bộ lọc tương tự
◮ Khó tính trực tiếp các hệ số của bộ lọc từ các chỉ tiêu kỹ
thuật
◮ Kỹ thuật thiết kế bộ lọc tương tự đã được phát triển từ rất
lâu, có nhiều thành quả để tận dụng.
◮ Nhiều bộ lọc IIR tương tự có công thức đơn giản, do vậy, bộ
lọc số tương ứng dễ thực hiện.
Tổng hợp bộ lọc IIR từ bộ lọc tương tự: Nguyên lý
◮ Xấp xỉ hàm truyền đạt hoặc đáp ứng xung:
Ha(s), ha(t)→ H(z), h(n).
◮ Bảo toàn một số đặc tính cơ bản trên miền tần số:
(i) Ánh xạ trục ảo trên mặt phẳng s lên vòng tròn đơn vị trên
mặt phẳng z.
(ii) Tính ổn định: hệ tương tự có các điểm cực ở nửa bên trái mặt
phẳng s → hệ số có các điểm cực nằm trong vòng tròn đơn vị
ở mặt phẳng z.
Phương pháp bất biến xung
Lấy mẫu đáp ứng xung ha(t)→ h(n) = ha(nTs). Tương tự như
định lý lấy mẫu, H(ejω) có dạng như hình vẽ (khi |Ωmax | ≤ piTs ).
0
0
1
1
Ts
Ω
Ha(jΩ)
H(ejω)
pi/Ts−pi/Ts
pi 2pi−pi−2pi ω
Phương pháp bất biến xung - Hàm truyền đạt
Hàm truyền đạt của bộ lọc tương tự:
Ha(s) =
∑
k
Ak
s − spk
Biến đổi Laplace ngược, lấy mẫu chu kỳ Ts , có thể tính được hàm
truyền đạt của bộ lọc số:
H(z) =
∑
k
Ak
1− espkTs z−1
Ví dụ: Cho bộ lọc tương tự có hàm truyền đạt
Ha(s) =
4
(s + 3)(s + 5)
(a) Hãy tìm hàm truyền đạt H(z) của bộ lọc số bằng phương
pháp bất biến xung
(b) Vẽ sơ đồ thực hiện bộ lọc số
Phương pháp bất biến xung - Tính ổn định
Nếu điểm cực của bộ lọc tương tự nằm bên trái mặt phẳng phức:
spk = σ + jΩ, σ < 0
thì điểm cực của bộ lọc số nằm trong vòng tròn đơn vị:
zpk = e
spkTs → |zpk | = eσTs < 1
jΩ
σ
σ 0
pi/Ts
−pi/Ts
Im{z}
Re{z}1−1
Phương pháp bất biến xung - Tính chất
◮ Duy trì được bậc và tính ổn định của bộ lọc tương tự
◮ Không áp dụng được cho tất cả các loại bộ lọc (thông cao,
chắn dải)
◮ Có thể xảy ra méo dạng đáp ứng tần số do chồng phổ
Phương pháp biến đổi song tuyến
Tránh hiện tượng chồng phổ, ánh xạ toàn bộ trục ảo jΩ trên mặt
phẳng s thành vòng tròn đơn vị trên mặt phẳng z .
Ha(s)→ H(z), s = 2
T
· 1− z
−1
1+ z−1
với T bất kỳ.
◮ Trục ảo σ = 0 ↔ vòng tròn đơn vị |z | = 1.
◮ Nửa trái mặt phẳng phức σ < 0 ↔ phần mặt phẳng nằm
trong vòng tròn đơn vị |z | < 1.
So với bộ lọc tương tự:
◮ Đáp ứng tần số giống nhau
◮ Đáp ứng xung có thể rất khác nhau
Phương pháp biến đổi song tuyến: Tính chất
Nếu s = σ + jΩ và z = re jω, dễ dàng tính được
ω = 2 arctan(
T
2
Ω), Ω =
2
T
tan(ω/2)
Ω
ω
pi
Các bước thiết kế:
1. Xấp xỉ các chỉ tiêu kỹ thuật của bộ lọc số sang bộ lọc tương
tự
2. Thiết kế bộ lọc tương tự
3. Áp dụng biến đổi song tuyến
s =
2
T
· 1− z
−1
1+ z−1
Phương pháp tương đương vi phân
Xấp xỉ: phương trình vi phân → phương trình sai phân, ví dụ:
d
dt
ya(t)→ 1
Ts
[y(n)− y(n − 1)]
Hàm truyền đạt:
Ha(s)→ H(z), s = 1− z
−1
Ts
Phương pháp biến đổi z thích ứng
Ánh xạ các điểm cực và điểm không:
Ha(s) =
∏M
r=1(s − s0r )∏N
k=1(s − spk)
→ H(z) =
∏M
r=1(1− es0rTs z−1)∏N
k=1(1− espkTs z−1)