Bài giảng Xử lý tín hiệu số - Chương 3: Discrete. Time systems - Hà Hoàng Kha

Chapter 3
Discrete-Time Systems
Click to edit Master subtitle styleHa Hoang Kha, Ph.D.
Ho Chi Minh City University of Technology
Email: hhkha@hcmut.edu.vn
Content
™ I t/ t t l ti hi f th tnpu ou pu re a ons p o e sys ems
™ Linear time-invariant (LTI) systems 
™ FIR d IIR fil
‰ convolution
 an ters
™ C li d bili f hausa ty an sta ty o t e systems
Ha H. Kha 2 Discrete-Time Systems
1. Discrete-time signal
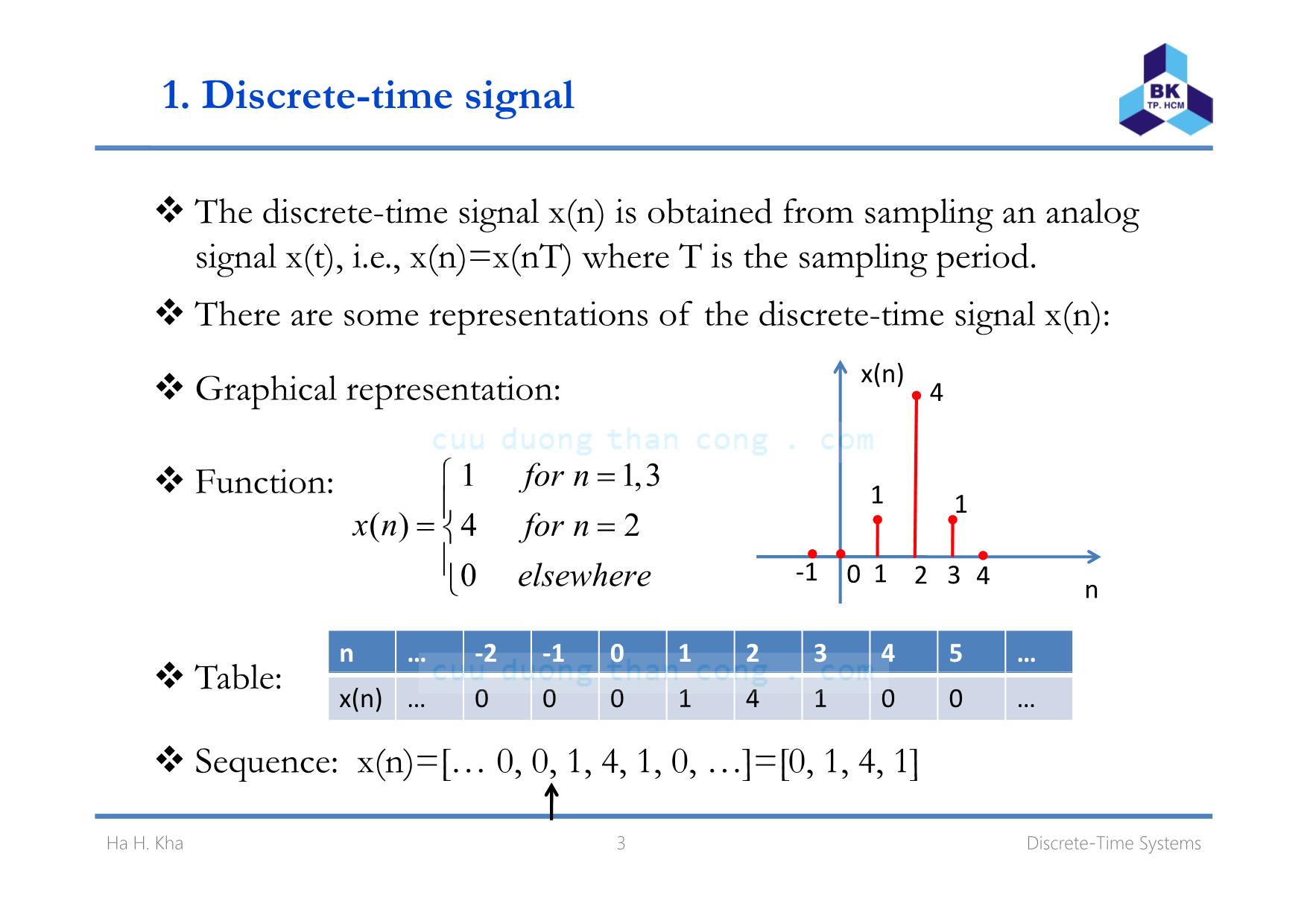
™ The discrete-time signal x(n) is obtained from sampling an analog 
signal (t) i e (n)= (nT) here T is the sampling period x , . ., x x w .
™ There are some representations of the discrete-time signal x(n):
™ Graphical representation:
⎧
x(n)
4
™ Function: 1 1,3
( ) 4 2
0
for n
x n for n
l h
=⎪= =⎨⎪⎩ 1 2 31 0 4
11
™ T bl
e sew ere
n  ‐2 ‐1 0 1 2 3 4 5 
n‐
a e: 
™ Sequence: x(n)=[ 0, 0, 1, 4, 1, 0, ]=[0, 1, 4, 1] 
x(n)  0 0 0 1 4 1 0 0 
3 Discrete-Time SystemsHa H. Kha
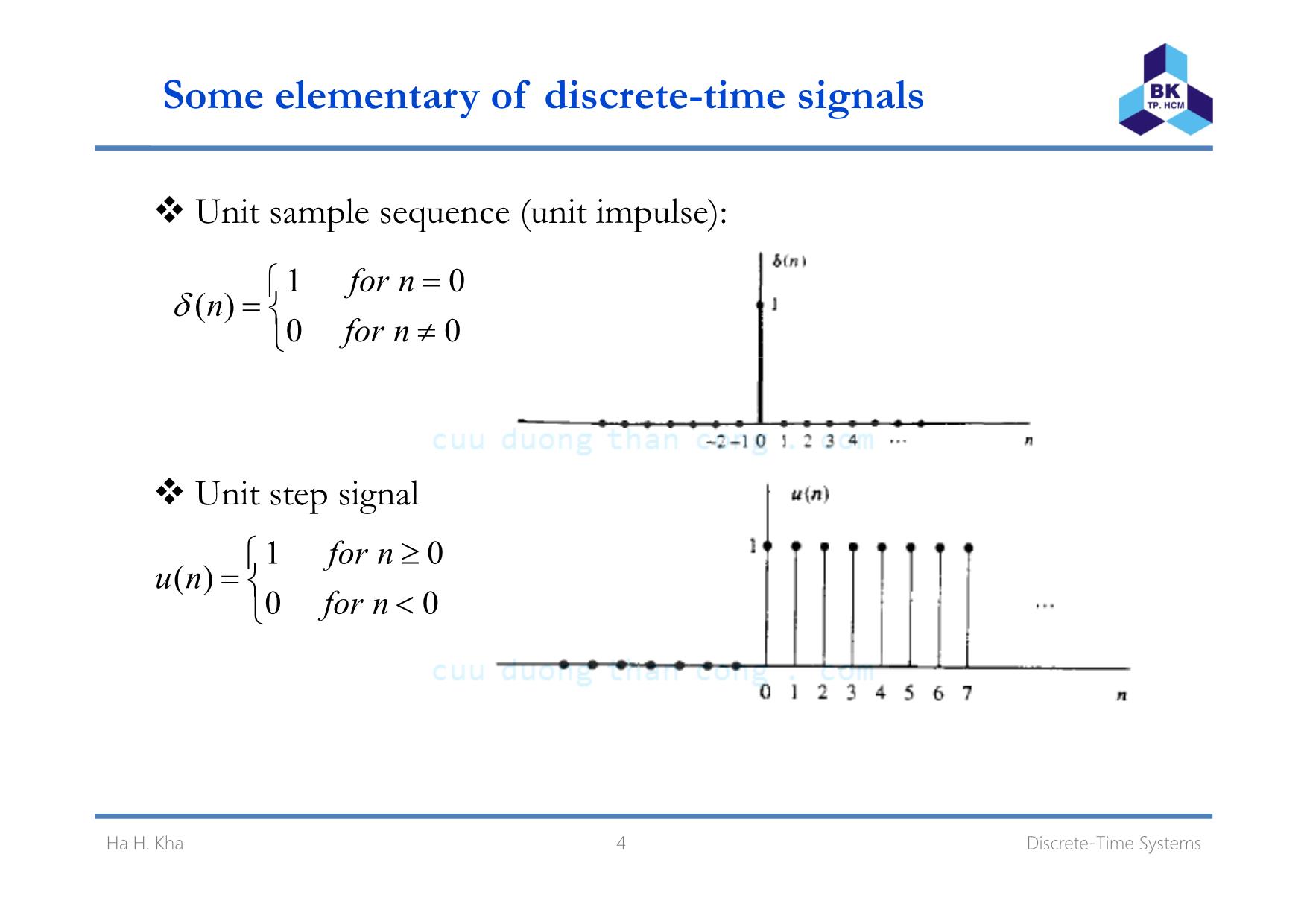
Some elementary of discrete-time signals
™ Unit sample sequence (unit impulse): 
1 0
( )
0 0
for n
n
for n
δ =⎧= ⎨ ≠⎩
™ Unit step signal
1 0
( )
for n ≥⎧⎨0 0u n for n= <⎩
4 Discrete-Time SystemsHa H. Kha
2. Input/output rules
™ A discrete-time system is a processor that transform an input 
seq ence (n) into an o tp t seq ence (n)u x u u u y .
™ Sample by sample processing:
Fig: Discrete-time system
- - 
that is, and so on. 
™ Block processing:
5 Discrete-Time SystemsHa H. Kha
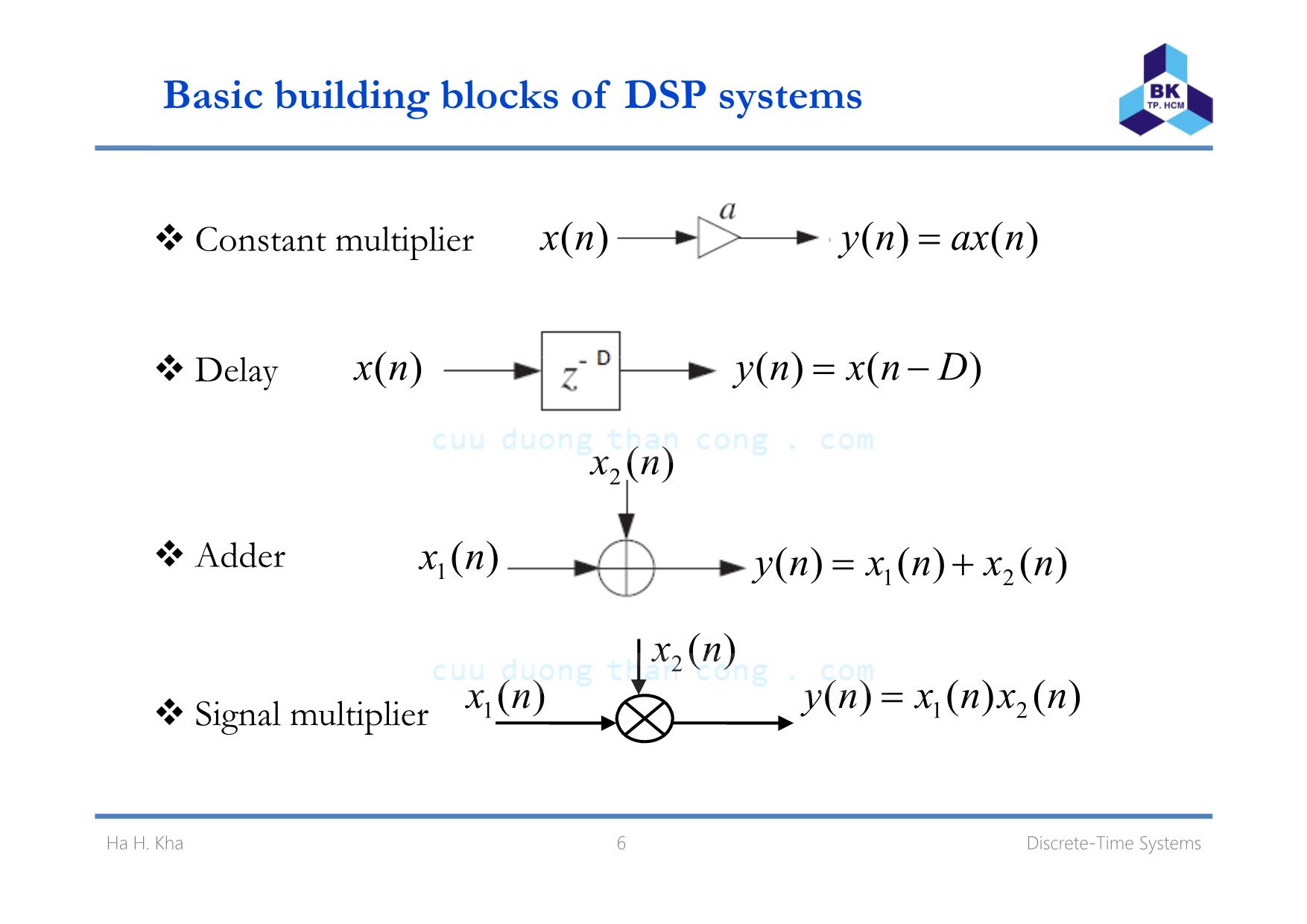
Basic building blocks of DSP systems
™ Constant multiplier )(nx )()( naxny =
)( )()( D™ D l
)(nx
nx nxny −=e ay
™ Adder )(1 nx
2
)()()( nxnxny += 21
)(2 nx
™ Signal multiplier )(1 nx )()()( 21 nxnxny =
6 Discrete-Time SystemsHa H. Kha
Example
™ Let x(n)={1, 3, 2, 5}. Find the output and plot the graph for the 
systems with input/out rules as follows: 
a) y(n)=2x(n)
b) y(n)=x(n-4)
c) y(n)=x(n)+x(n 1) -
7 Discrete-Time SystemsHa H. Kha
Example
™ A weighted average system y(n)=2x(n)+4x(n-1)+5x(n-2). Given the 
input signal x(n)=[x0,x1, x2, x4 ]
a) Find the output y(n) by sample-sample processing method?
b) Find the output y(n) by block processing method.
c) Plot the block diagram to implement this system from basic 
building blocks ?
8 Discrete-Time SystemsHa H. Kha
3. Linearity and time invariance
™ A linear system has the property that the output signal due to a 
linear combination of t o inp t signals can be obtained b forming w u y 
the same linear combination of the individual outputs.
Fig: Testing linearity 
™ If y(n)=a1y1(n)+a2y2(n) ∀ a1, a2Æ linear system. Otherwise, the 
system is nonlinear.
9 Discrete-Time SystemsHa H. Kha
Example
™ Test the linearity of the following discrete-time systems:
a) y(n)=nx(n)
b) y(n)=x(n2)
c) y(n)=x2(n)
d) y(n)=Ax(n)+B
10 Discrete-Time SystemsHa H. Kha
3. Linearity and time invariance
™ A time-invariant system is a system that its input-output 
characteristics do not change ith time w . 
Fig: Testing time invariance
™ If yD(n)=y(n-D) ∀ DÆ time-invariant system. Otherwise, the 
system is time-variant.
11 Discrete-Time SystemsHa H. Kha
Example
™ Test the time-invariance of the following discrete-time systems:
a) y(n)=x(n)-x(n-1)
b) y(n)=nx(n)
c) y(n)=x(-n)
d) y(n)=x(2n)
12 Discrete-Time SystemsHa H. Kha
4. Impulse response
™ Linear time-invariant (LTI) systems are characterized uniquely by 
their impulse response sequence h(n), which is defined as the 
response of the systems to a unit impulse δ(n).
Fig: Impulse response of an LTI system 
i D l d i l f T
13 Discrete-Time Systems
F g: e aye mpu se responses o an L I system
Ha H. Kha
5. Convolution of LTI systems
Fig: Response to linear combination of inputs 
™ Convolution:
(LTI form))()()()()( nhnxmnhmxny
m
∗=−=∑
)()()()()( nxnhmnxmhny
m
∗=−=∑ (direct form)
14 Discrete-Time SystemsHa H. Kha
5. FIR and IIR filters
™ A finite impulse response (FIR) filter has impulse response h(n) 
that extend only over a finite time interval say 0 ≤n ≤ M , .
Fi FIR i lg: mpu se response
™M: filter order; Lh=M+1: the length of impulse response 
™ h={h0, h1, , hM} is referred by various name such as filter 
coefficients, filter weights, or filter taps.
∑ −=∗= M mnxmhnxnhny )()()()()(™ FIR filtering equation:
15 Discrete-Time Systems
=m 0
Ha H. Kha
Example
™ The third-order FIR filter has the impulse response h=[1, 2, 1, -1] 
a) Find the I/O equation, i.e., the relationship of the input x(n) and the 
output y(n) ?
b) Given x=[1, 2, 3, 1], find the output y(n) ? 
16 Discrete-Time SystemsHa H. Kha
5. FIR and IIR filters
™ A infinite impulse response (IIR) filter has impulse response h(n) 
of infinite duration say 0 ≤n ≤ ∞ , .
Fi IIR i lg: mpu se response
∑∞ −=∗= )()()()()( mnxmhnxnhny™ IIR filtering equation:
=0m
™ The I/O equation of IIR filters are expressed as the recursive 
difference equation.
17 Discrete-Time SystemsHa H. Kha
Example
™ Determine the output of the LTI system which has the impulse 
r p n h(n)= n (n) | |≤ 1 h n th inp t i th nit t p i n les o se a u , a w e e u s e u s e s g a 
x(n)=u(n) ?
nmn +1™ Remark:
r
rrr
mk
k
−
−=
=
∑ 1
™When n= ∞ and|r|≤ 1 
r
rr
m
k
k
−=∑
∞
1
18 Discrete-Time Systems
m=
Ha H. Kha
Example
™ Assume the IIR filter has a casual h(n) defined by
⎨⎧ == 02)( 1
nfor
nh
) Fi d h I/O diff i ?
⎩ ≥− 1)5.0(4 nforn
a n t e erence equat on 
b) Find the difference equation for h(n)? 
19 Discrete-Time SystemsHa H. Kha
6. Causality and Stability
Fig: Causal, anticausal, and mixed signals
™ LTI systems can also classified in terms of causality depending on 
whether h(n) is casual, anticausal or mixed. 
™ A system is stable (BIBO) if bounded inputs (|x(n)| ≤A) always 
generate bounded outputs (|y(n)| ≤B).
™ A LTI system is stable ∞<⇔ ∑∞ nh |)(|
20 Discrete-Time Systems
−∞=n
Ha H. Kha
Example
™ Consider the causality and stability of the following systems:
a) h(n)=(0.5)nu(n)
b) h(n)=-(0.5)nu(-n-1)
21 Discrete-Time SystemsHa H. Kha
Homework
™ Problems: 3.1, 3.2, 3.3, 3.4, 3.5, 3.6
22 Discrete-Time SystemsHa H. Kha