Bài giảng Xử lý tín hiệu số - Chương 3: Các thuật toán FFT và ứng dụng - Đặng Quang Hiếu
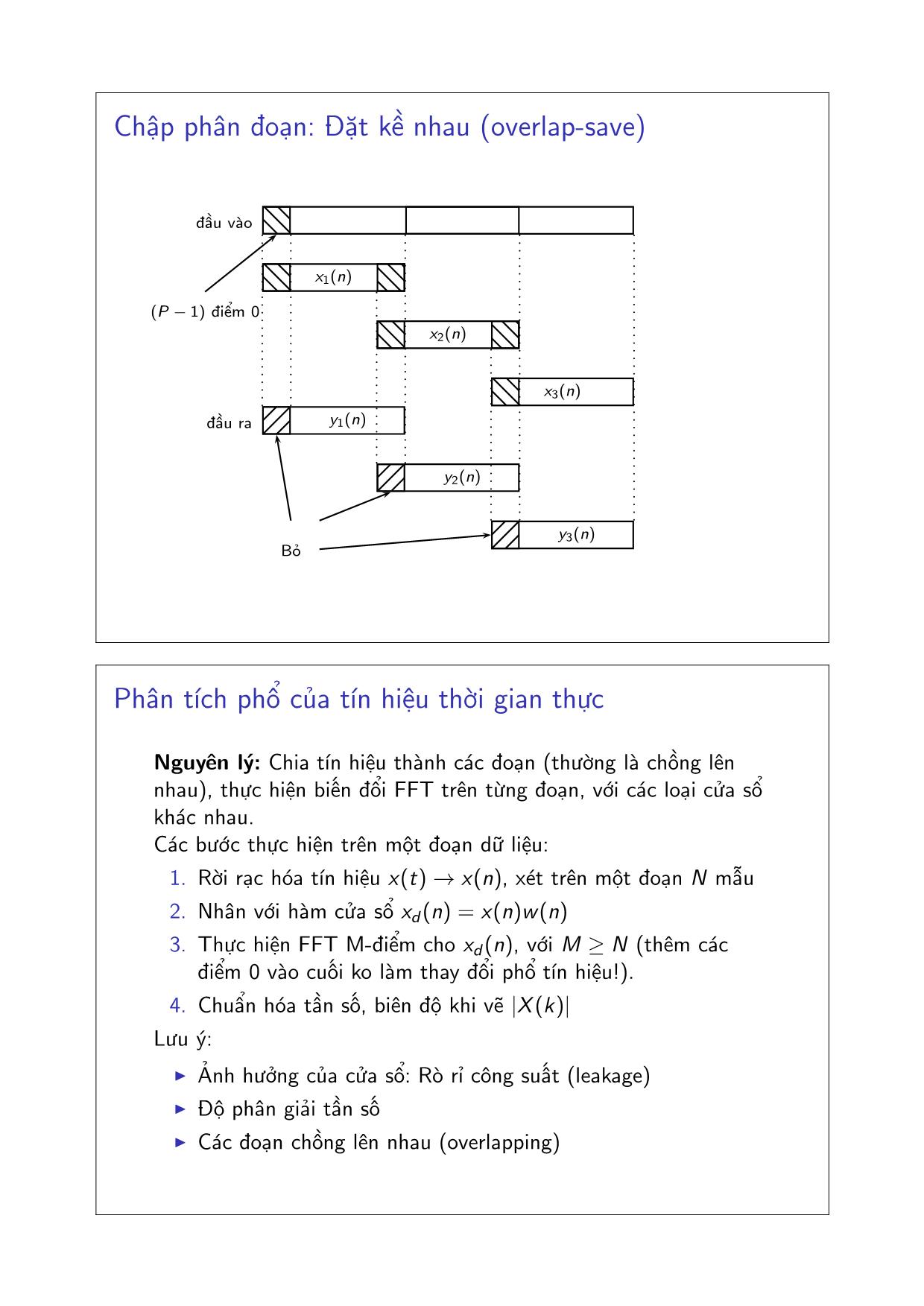
Nguyên lý: Chia tín hiệu thành các đoạn (thường là chồng lên
nhau), thực hiện biến đổi FFT trên từng đoạn, với các loại cửa sổ
khác nhau.
Các bước thực hiện trên một đoạn dữ liệu:
1. Rời rạc hóa tín hiệu x(t) → x(n), xét trên một đoạn N mẫu
2. Nhân với hàm cửa sổ xd(n) = x(n)w(n)
3. Thực hiện FFT M-điểm cho xd(n), với M ≥ N (thêm các
điểm 0 vào cuối ko làm thay đổi phổ tín hiệu!).
4. Chuẩn hóa tần số, biên độ khi vẽ |X (k)|
Lưu ý:
Ảnh hưởng của cửa sổ: Rò rỉ công suất (leakage)
Độ phân giải tần số
Các đoạn chồng lên nhau (overlapping)

Trang 1
Trang 2
Trang 3

Trang 4

Trang 5
Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Bạn đang xem tài liệu "Bài giảng Xử lý tín hiệu số - Chương 3: Các thuật toán FFT và ứng dụng - Đặng Quang Hiếu", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Xử lý tín hiệu số - Chương 3: Các thuật toán FFT và ứng dụng - Đặng Quang Hiếu

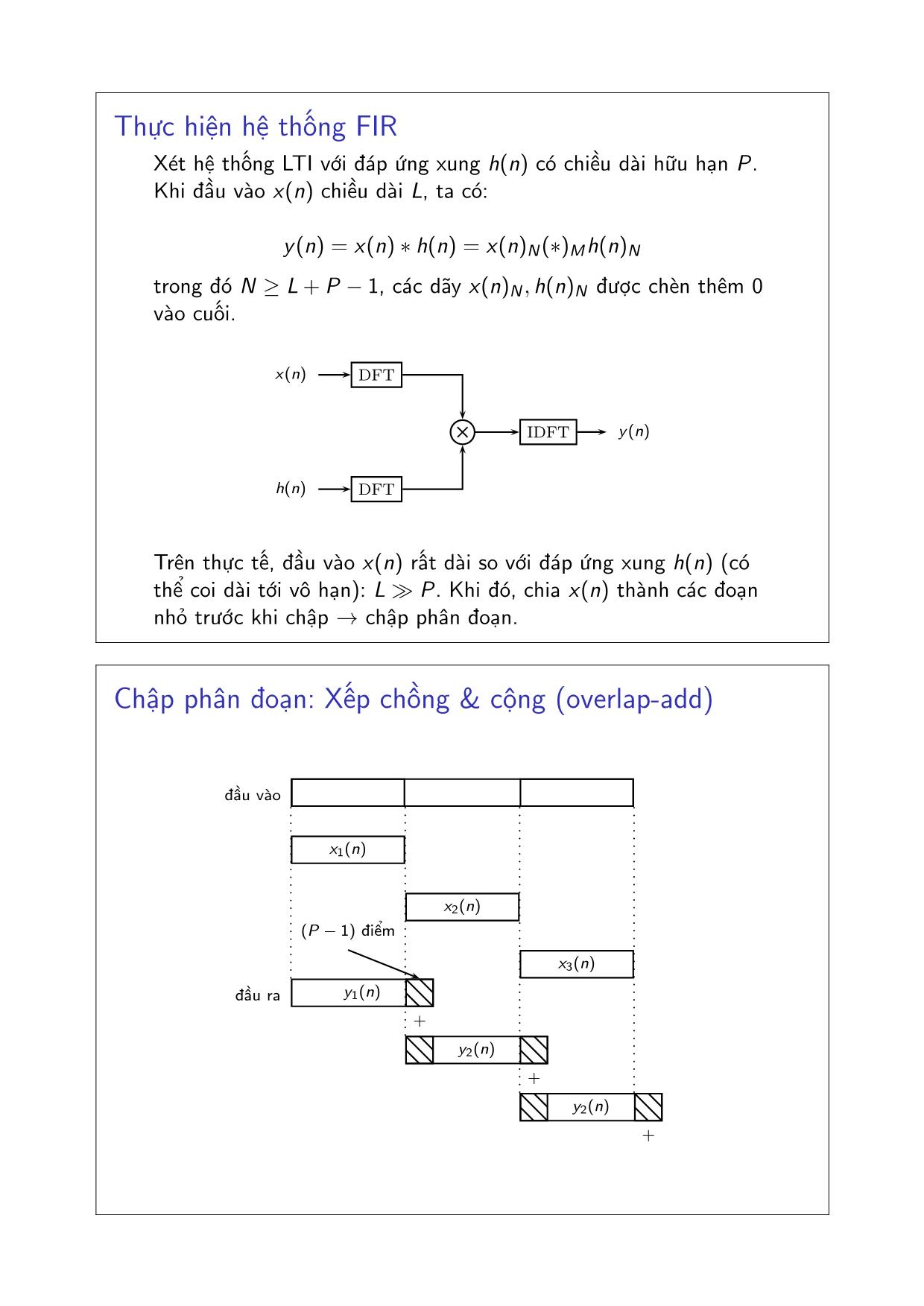
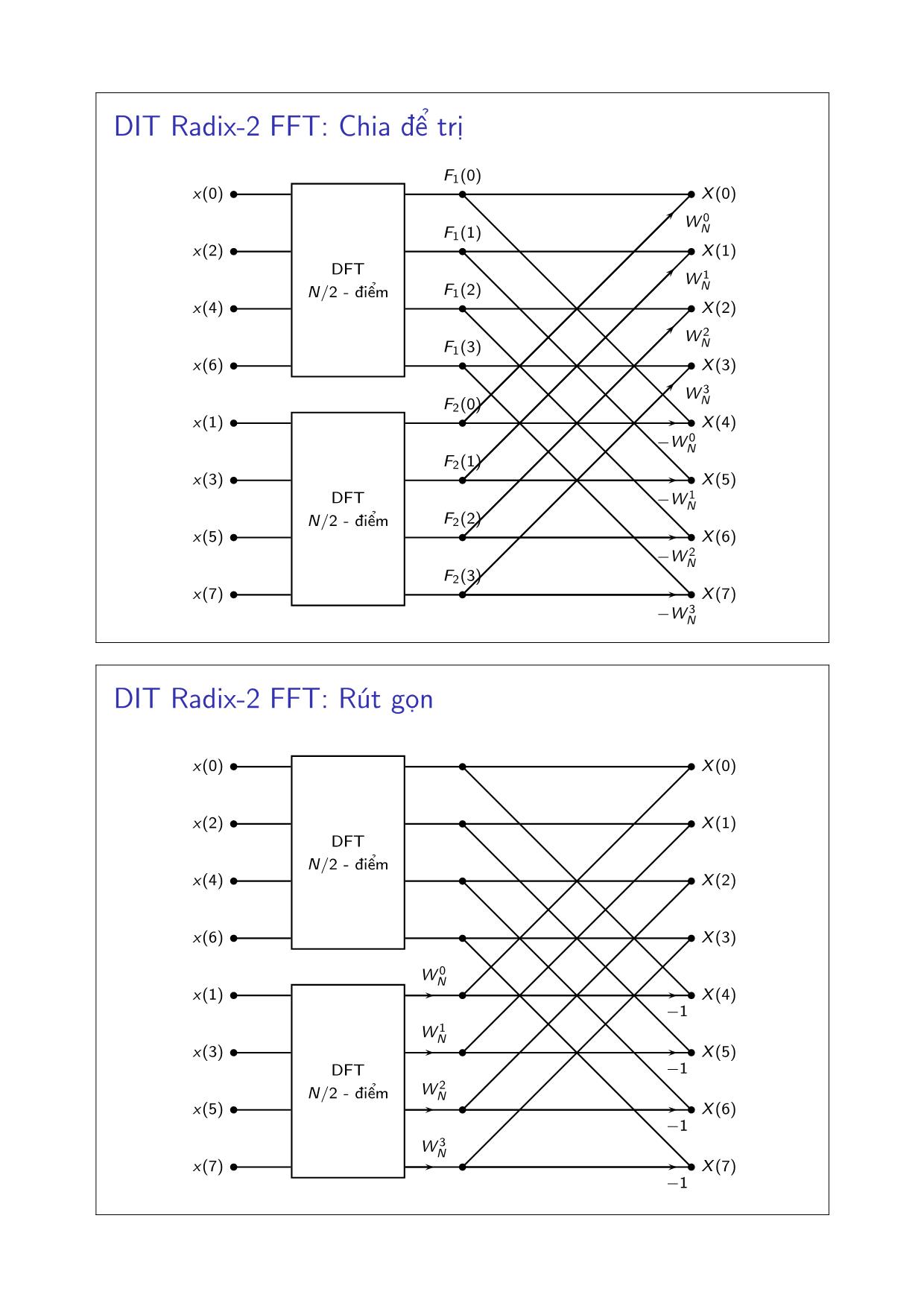
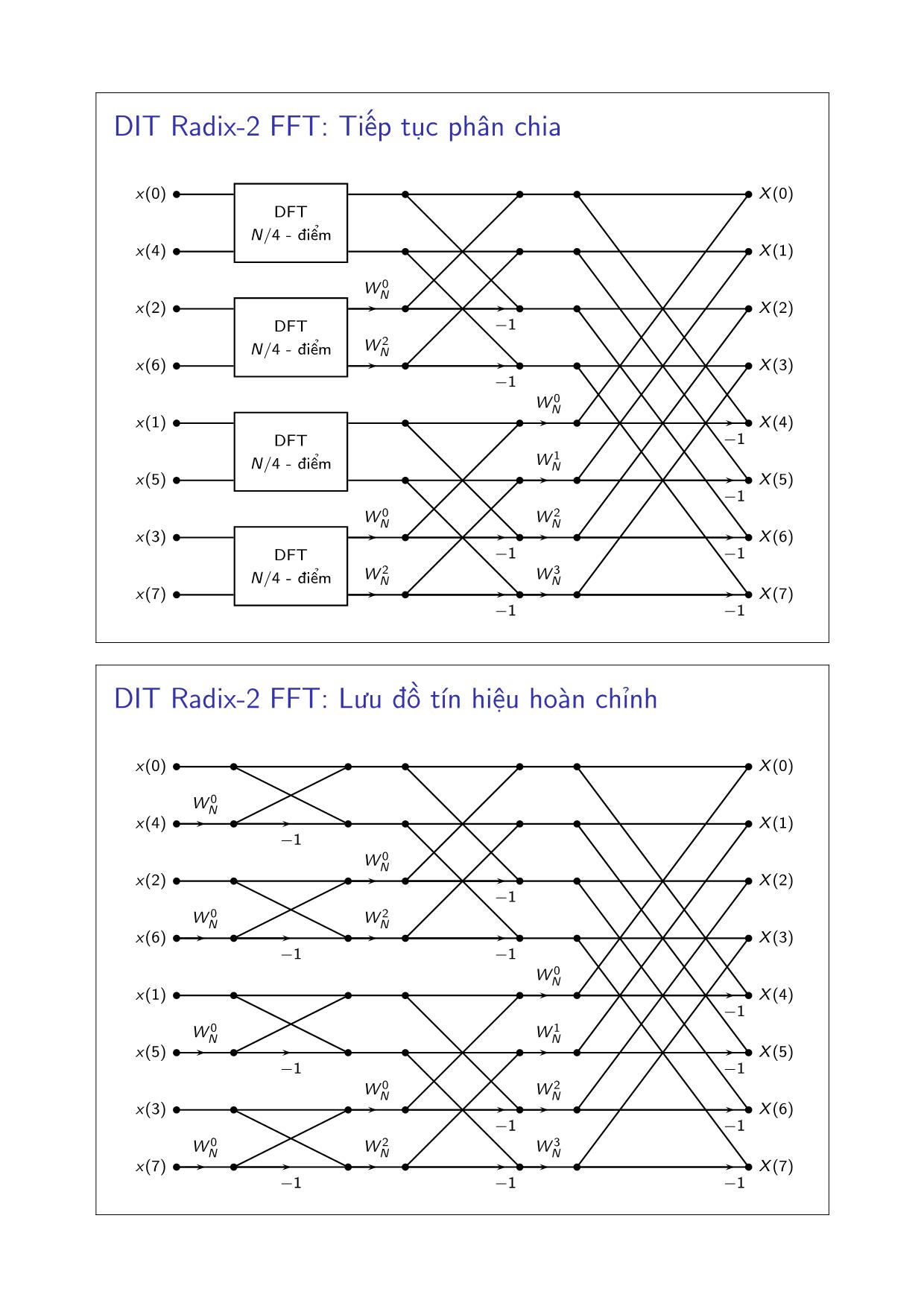
ET4020 - Xử lý tín hiệu số Chương 3: Các thuật toán FFT và ứng dụng TS. Đặng Quang Hiếu Trường Đại học Bách Khoa Hà Nội Viện Điện tử - Viễn thông Năm học 2012 - 2013 Outline Ứng dụng của DFT Các thuật toán FFT Thực hiện hệ thống FIR Xét hệ thống LTI với đáp ứng xung h(n) có chiều dài hữu hạn P . Khi đầu vào x(n) chiều dài L, ta có: y(n) = x(n) ∗ h(n) = x(n)N(∗)Mh(n)N trong đó N ≥ L+ P − 1, các dãy x(n)N , h(n)N được chèn thêm 0 vào cuối. x(n) h(n) y(n) DFT DFT IDFT Trên thực tế, đầu vào x(n) rất dài so với đáp ứng xung h(n) (có thể coi dài tới vô hạn): L≫ P . Khi đó, chia x(n) thành các đoạn nhỏ trước khi chập → chập phân đoạn. Chập phân đoạn: Xếp chồng & cộng (overlap-add) đầu vào x1(n) đầu ra y1(n) (P − 1) điểm x2(n) y2(n) x3(n) y2(n) + + + Chập phân đoạn: Đặt kề nhau (overlap-save) đầu vào (P − 1) điểm 0 x1(n) đầu ra y1(n) x2(n) y2(n) x3(n) y3(n) Bỏ Phân tích phổ của tín hiệu thời gian thực Nguyên lý: Chia tín hiệu thành các đoạn (thường là chồng lên nhau), thực hiện biến đổi FFT trên từng đoạn, với các loại cửa sổ khác nhau. Các bước thực hiện trên một đoạn dữ liệu: 1. Rời rạc hóa tín hiệu x(t)→ x(n), xét trên một đoạn N mẫu 2. Nhân với hàm cửa sổ xd(n) = x(n)w(n) 3. Thực hiện FFT M-điểm cho xd(n), với M ≥ N (thêm các điểm 0 vào cuối ko làm thay đổi phổ tín hiệu!). 4. Chuẩn hóa tần số, biên độ khi vẽ |X (k)| Lưu ý: ◮ Ảnh hưởng của cửa sổ: Rò rỉ công suất (leakage) ◮ Độ phân giải tần số ◮ Các đoạn chồng lên nhau (overlapping) Outline Ứng dụng của DFT Các thuật toán FFT Độ phức tạp tính toán của DFT X (k) = N−1∑ n=0 x(n)W knN , 0 ≤ k ≤ N − 1 trong đó, WN = e −j2pi/N . Để tính trực tiếp mỗi giá trị của X (k): ◮ N phép nhân phức (4N phép nhân thực và 2N phép cộng thực) ◮ N − 1 phép cộng phức (2N − 2 phép cộng thực) ◮ 2N phép tính giá trị các hàm sin, cos. Độ phức tạp tính toán của DFT - N điểm: O(N2). DIT Radix-2 FFT (phân chia theo thời gian, cơ số 2) Xét N = 2v , chia x(n) thành hai dãy chỉ số chẵn x(2m) và chỉ số lẻ x(2m + 1): X (k) = N−1∑ n=0 x(n)W knN , k = 0, 1, · · · , (N − 1) = N/2−1∑ m=0 x(2m)W k2mN + N/2−1∑ m=0 x(2m + 1)W k(2m+1) N Với k = 0, 1, . . . ,N/2, ta có: X (k) = N/2−1∑ m=0 x(2m)W kmN/2 +W k N N/2−1∑ m=0 x(2m + 1)W kmN/2 = F1(k) +W k NF2(k) DIT Radix-2 FFT: Độ phức tạp tính toán Nhận xét: F1(k + N/2) = F1(k) F2(k + N/2) = F2(k) W k+N/2 N = −W kN do vậy, X (k + N 2 ) = F1(k)−W kNF2(k) X (k) = F1(k) +W k NF2(k) Nếu tính toán trực tiếp F1(k) và F2(k), tổng số phép nhân phức là: 2(N/2)2 + N/2 DIT Radix-2 FFT: Chia để trị b b b X (0) b b b X (1) b b b X (2) b b b X (3) b b b X (4) b b b X (5) b b b X (6) b b b X (7) x(0) x(2) x(4) x(6) x(1) x(3) x(5) x(7) F1(0) F1(1) F1(2) F1(3) F2(0) F2(1) F2(2) F2(3) DFT N/2 - điểm DFT N/2 - điểm −W 0N W 0N −W 1N W 1N −W 2N W 2N −W 3N W 3N DIT Radix-2 FFT: Rút gọn b b b X (0) b b b X (1) b b b X (2) b b b X (3) b b b X (4) b b b X (5) b b b X (6) b b b X (7) x(0) x(2) x(4) x(6) x(1) x(3) x(5) x(7) DFT N/2 - điểm DFT N/2 - điểm −1 W 0N −1 W 1N −1 W 2N −1 W 3N DIT Radix-2 FFT: Tiếp tục phân chia b b b b b X (0) b b b b b X (1) b b b b b X (2) b b b b b X (3) b b b b b X (4) b b b b b X (5) b b b b b X (6) b b b b b X (7) x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7) DFT N/4 - điểm DFT N/4 - điểm DFT N/4 - điểm DFT N/4 - điểm −1 W 0N −1 W 1N −1 W 2N −1 W 3N −1 −1 W 0N W 2N −1 −1 W 0N W 2N DIT Radix-2 FFT: Lưu đồ tín hiệu hoàn chỉnh b b b b b b b X (0) b b b b b b b X (1) b b b b b b b X (2) b b b b b b b X (3) b b b b b b b X (4) b b b b b b b X (5) b b b b b b b X (6) b b b b b b b X (7) x(0) x(4) x(2) x(6) x(1) x(5) x(3) x(7) −1 W 0N −1 W 1N −1 W 2N −1 W 3N −1 −1 W 0N W 2N −1 −1 W 0N W 2N −1 W 0N −1 W 0N −1 W 0N −1 W 0N DIT Radix-2 FFT: Sơ đồ cánh bướm b b b b −W rN W rN Xm−1(p) Xm−1(q) Xm(p) Xm(q) Hình: Sơ đồ cánh bướm cơ bản b b b b b b −1W rN Xm−1(p) Xm−1(q) Xm(p) Xm(q) Hình: Sơ đồ cánh bướm rút gọn Tính toán tại chỗ và đảo bit Xm(p) = Xm−1(p) +W rNXm−1(q) Xm(q) = Xm−1(p) −W rNXm−1(q) Không cần có bộ nhớ trung gian! Khi đó, cần đảo thứ tự tại đầu vào (chặng 0): Thứ tự Nhị phân Đảo bit Giá trị X0(0) 000 000 x(0) X0(1) 001 100 x(4) X0(2) 010 010 x(2) X0(3) 011 110 x(6) X0(4) 100 001 x(1) X0(5) 101 101 x(5) X0(6) 110 011 x(3) X0(7) 111 111 x(7) DIF Radix-2 FFT (phân chia theo tần số, cơ số 2) X (k) = N−1∑ n=0 x(n)W knN , k = 0, 1, · · · , (N − 1) = N/2−1∑ m=0 x(n)W knN + N−1∑ n=N/2 x(n)W knN = N/2−1∑ m=0 x(n)W knN + N/2−1∑ n=0 x(n + N/2)W kN/2 N W kn N = N/2−1∑ m=0 [x(n) + (−1)kx(n + N/2)]W knN DIF Radix-2 FFT: Độ phức tạp tính toán Tách X (k) thành hai dãy có chỉ số chẵn, lẻ: X (2k) = N/2−1∑ m=0 [x(n) + x(n + N/2)]W knN/2 X (2k + 1) = N/2−1∑ m=0 [x(n)− x(n + N/2)]W nNW knN/2 Độ phức tạp tính toán: (N/2) log2N phép nhân phức và N log2N phép cộng phức. b b b b b b −1 W rN Xm−1(p) Xm−1(q) Xm(p) Xm(q) Hình: Sơ đồ cánh bướm DIF Radix-2 FFT: Lưu đồ tín hiệu hoàn chỉnh b b b b b b bx(0) b b b b b b bx(1) b b b b b b bx(2) b b b b b b bx(3) b b b b b b bx(4) b b b b b b bx(5) b b b b b b bx(6) b b b b b b bx(7) X (0) X (4) X (2) X (6) X (1) X (5) X (3) X (7) −1 W 0N −1 W 1N −1 W 2N −1 W 3N −1 −1 W 0N W 2N −1 −1 W 0N W 2N −1 W 0N −1 W 0N −1 W 0N −1 W 0N Bài về nhà 1. Vẽ lưu đồ tín hiệu cho thuật toán FFT trường hợp N = 16, phân chia theo tần số / thời gian, cơ số 2. 2. Tìm hiểu thuật toán FFT cơ số 4. 3. Triển khai các thuật toán FFT đã học bằng ngôn ngữ C, so sánh tốc độ. 4. Sử dụng bộ DFT N-điểm để tính DFT 2N-điểm của dãy số thực. 5. Tính toán tối ưu DFT N-điểm của hai dãy số thực (cùng chiều dài hữu hạn N).
File đính kèm:
 bai_giang_xu_ly_tin_hieu_so_chuong_3_cac_thuat_toan_fft_va_u.pdf
bai_giang_xu_ly_tin_hieu_so_chuong_3_cac_thuat_toan_fft_va_u.pdf

