Bài giảng Xử lý tín hiệu số - Chương 2: Quantization - Hà Hoàng Kha

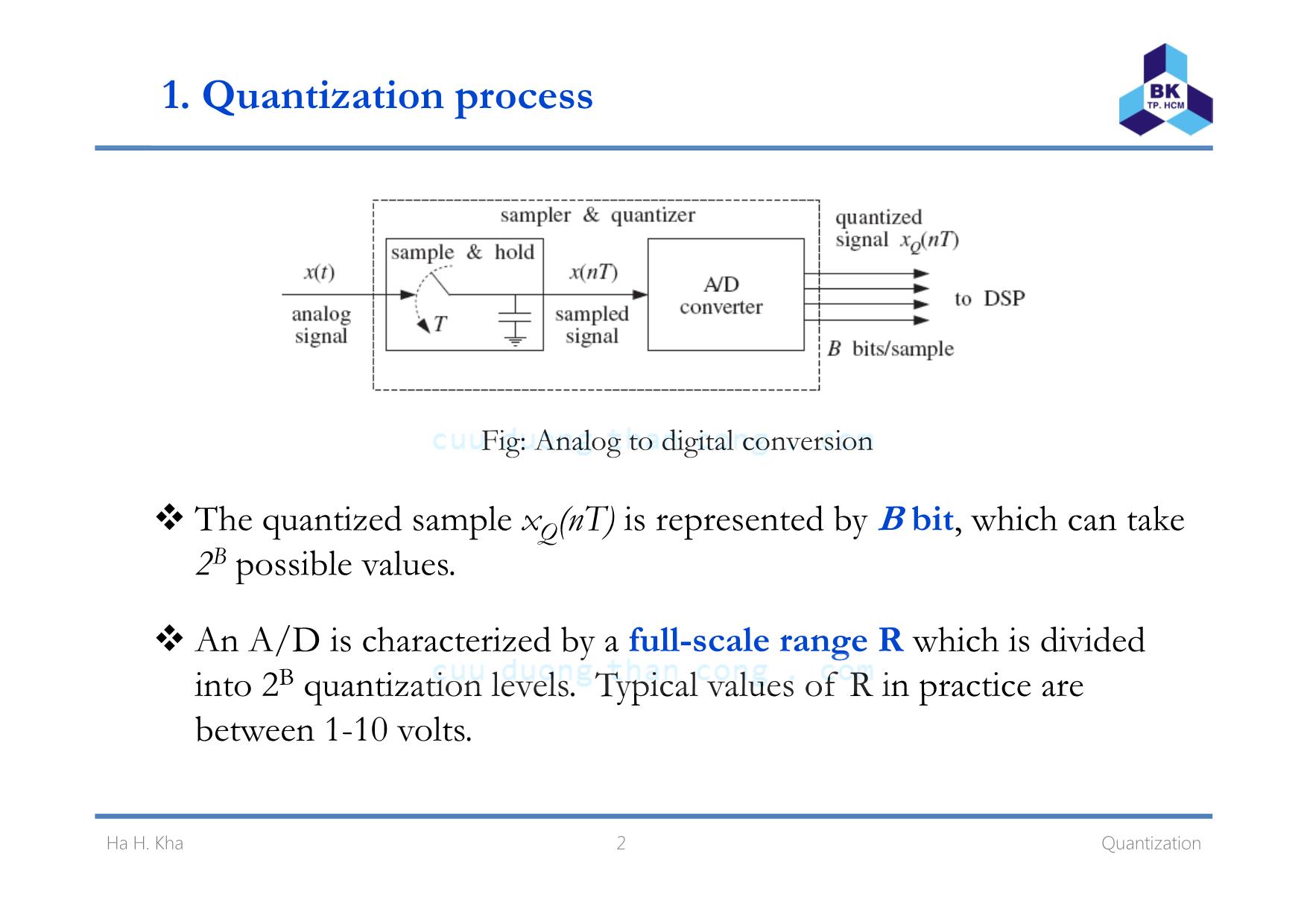
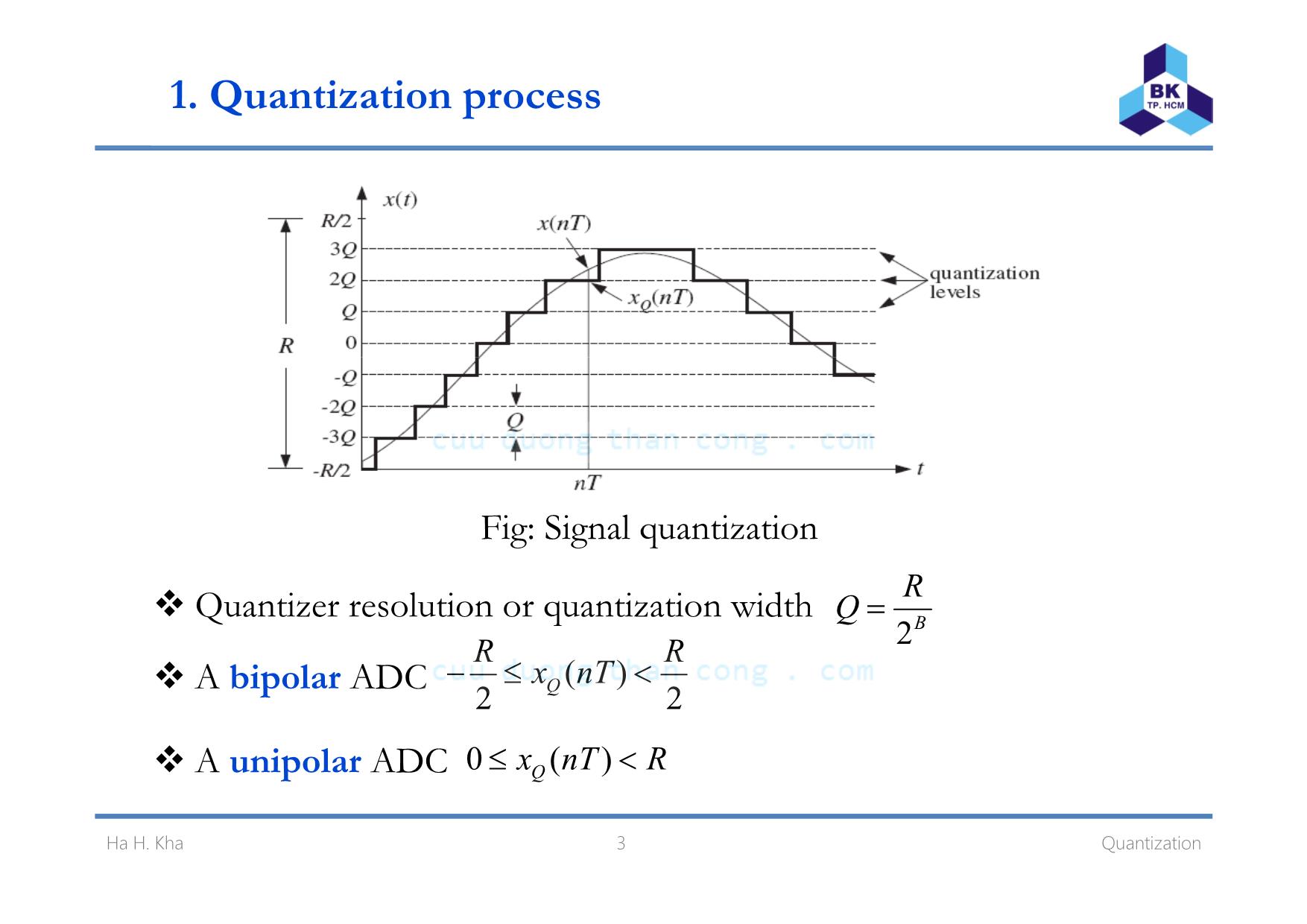
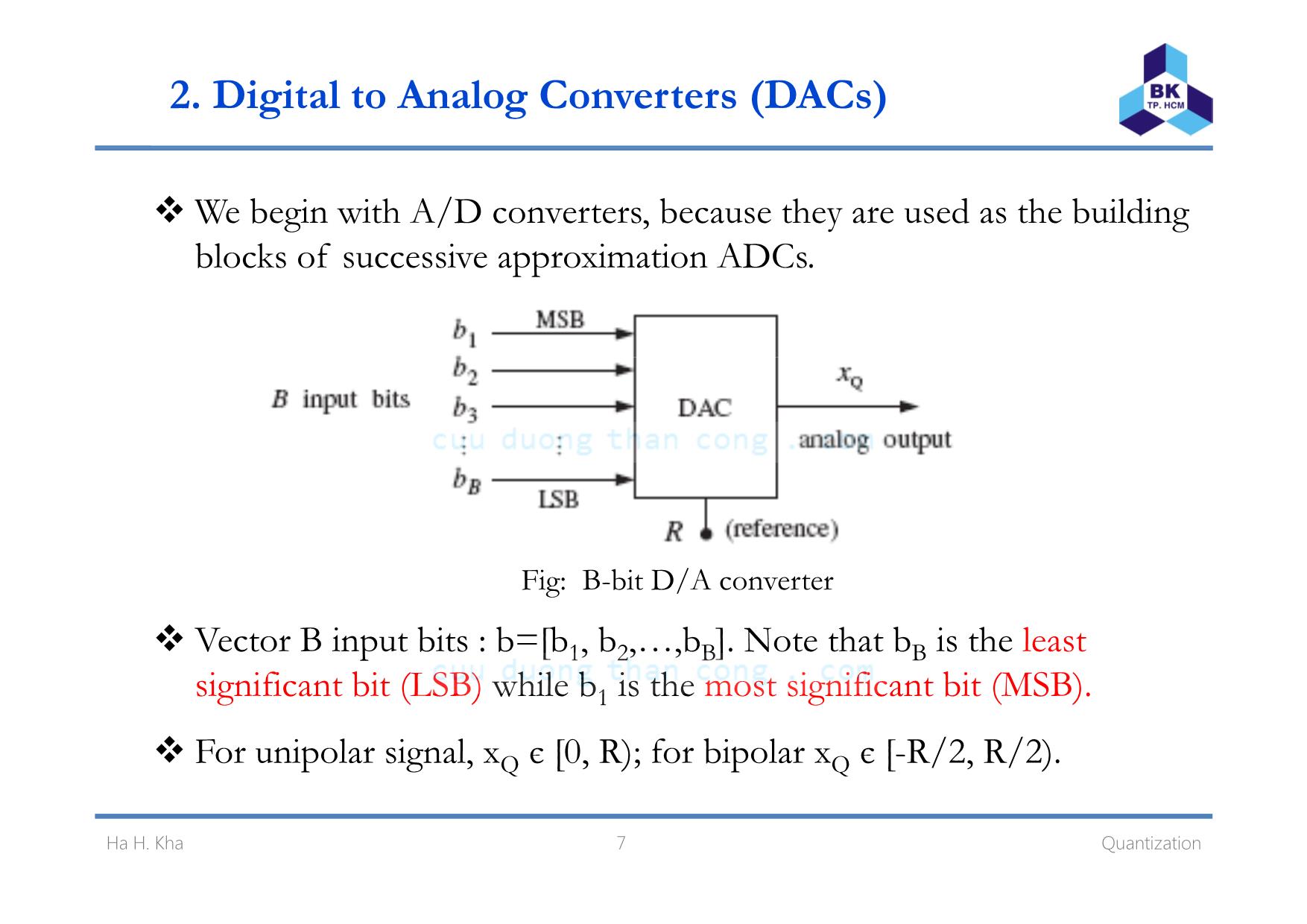
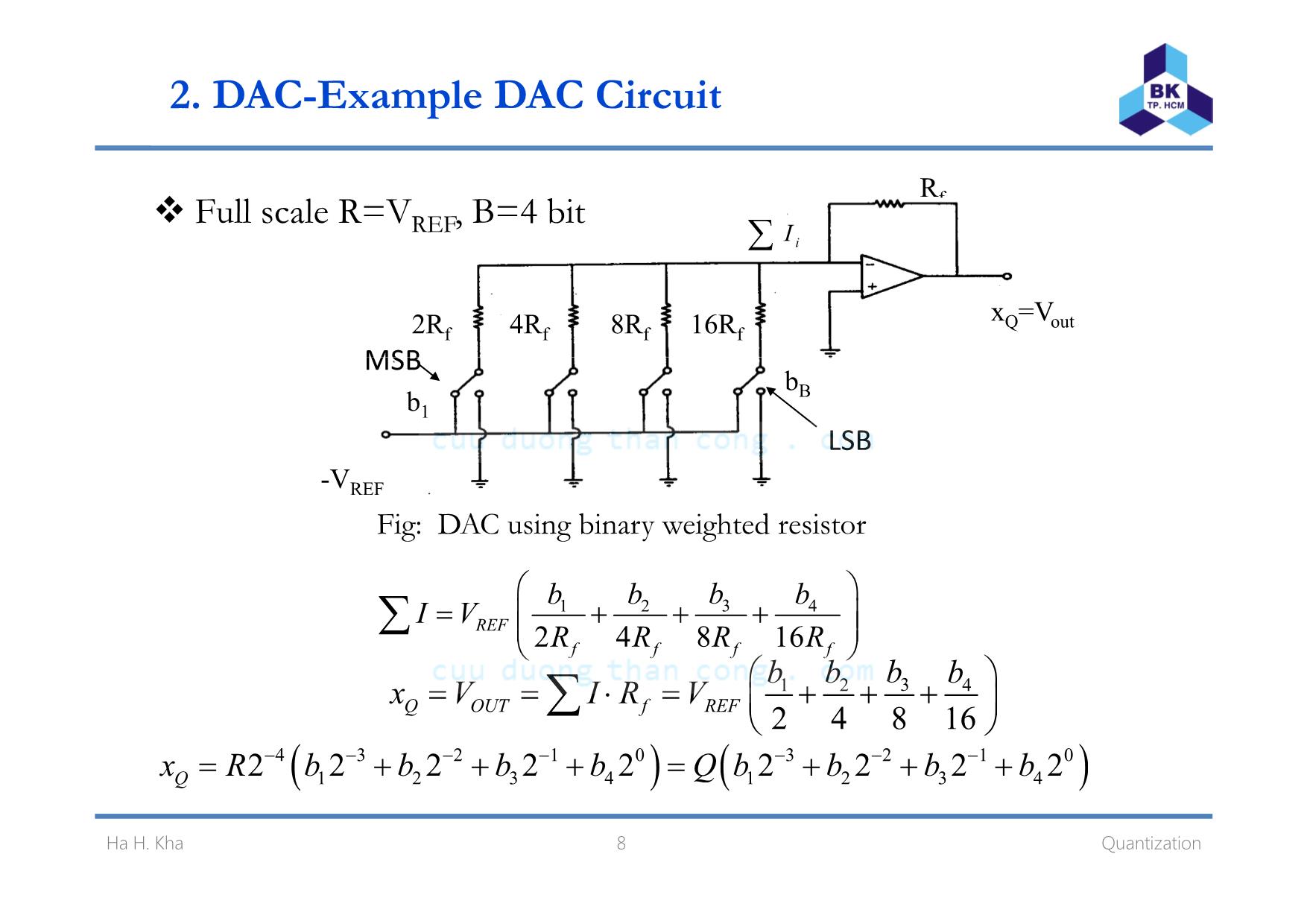
Chapter 2
Quantization
Click to edit Master subtitle styleHa Hoang Kha, Ph.D.
Ho Chi Minh City University of Technology
Email: hhkha@hcmut.edu.vn
1. Quantization process
Fig: Analog to digital conversion
™ The quantized sample xQ(nT) is represented by B bit, which can take 
2B possible values . 
™ An A/D is characterized by a full-scale range R which is divided 
B l l T l l finto 2 quantization eve s. ypica va ues o R in practice are 
between 1-10 volts.
Ha H. Kha 2 Quantization
1. Quantization process
Fig: Signal quantization
™ Quantizer resolution or quantization width 
2B
RQ =
™ A bip l ADC ( )R Rx nT≤ < o ar 2 2Q−
™ A unipolar ADC 0 ( )Qx nT R≤ <
3 QuantizationHa H. Kha
1. Quantization process –Quantization error 
™ Quantization by rounding: replace each value x(nT) by the nearest
q antization le elu v . 
™ Quantization by truncation: replace each value x(nT) by its below 
( ) ( ) ( )Qe nT x nT x nT= −
quantization level. 
™ Quantization error: 
™ Consider rounding quantization: 
2 2
Q Qe− ≤ ≤
i if b bili d i f i i
4 Quantization
F g: Un orm pro a ty ens ty o quant zat on error
Ha H. Kha
1. Quantization process –Quantization error 
™ The mean value of quantization error
/2 /2 1( ) 0
Q Q
e ep e de e de
Q
= = =∫ ∫
™ The mean-square error (power)
/2 /2Q Q− −
/2 /2 2
2 2 2 2 1( )
Q Q Qe e p e de e deσ = = = =∫ ∫ 
/2 /2 12Q Q Q− −
™ Root mean square (rms) error: 2 Qe eσ= = =- - 
12rms
™ R and Q are the ranges of the signal and quantization noise, then the 
signal to noise ratio (SNR) or dynamic range of the quantizer is 
defined as 
⎛ ⎞
10 10 1020 log 20log (2 ) log (2) 6
B
dB
RSNR B B dB
Q
= = = =⎜ ⎟⎝ ⎠
which is referred to as 6 dB bit rule
5 Quantization
 .
Ha H. Kha
1. Quantization process –Example
™ In a digital audio application, the signal is sampled at a rate of 44 
d h l d A/ hKHz an eac samp e quantize using an D converter aving a 
full-scale range of 10 volts. Determine the number of bits B if the 
rms quantinzation error mush be kept below 50 microvolts Then . , 
determine the actual rms error and the bit rate in bits per second. 
6 QuantizationHa H. Kha
2. Digital to Analog Converters (DACs)
™We begin with A/D converters, because they are used as the building 
blocks of s ccessi e appro imation ADCs u v x . 
Fig: B-bit D/A converter
™ Vector B input bits : b=[b1, b2,,bB]. Note that bB is the least 
f b h l b h f bsigni icant it (LSB) w i e 1 is t e most signi icant it (MSB). 
™ For unipolar signal, xQ є [0, R); for bipolar xQ є [-R/2, R/2). 
7 QuantizationHa H. Kha
2. DAC-Example DAC Circuit
Rf
∑ iI™ Full scale R=VREF, B=4 bit
16Rf8Rf4Rf2Rf
xQ=Vout
MSB
LSB
b1
bB
Fig: DAC using binary weighted resistor
-VREF 
31 2 4
2 4 8 16REF f f f f
bb b bI V
R R R R
⎛ ⎞= + + +⎜ ⎟⎜ ⎟⎝ ⎠∑
bb b b⎛ ⎞31 2 4
2 4 8 16Q OUT f REF
x V I R V= = ⋅ = + + +⎜ ⎟⎝ ⎠∑( ) ( )4 3 2 1 0 3 2 1 01 2 3 4 1 2 3 42 2 2 2 2 2 2 2 2Qx R b b b b Q b b b b− − − − − − −= + + + = + + +
8 QuantizationHa H. Kha
2. D/A Converters
™ Unipolar natural binary 1 21 2( 2 2 ... 2 )BQ Bx R b b b Qm− − −= + + + =
where m is the integer whose binary representation is b=[b1, b2,,bB]. 
1 2 02 2 2B Bm b b b− −= + + +1 2 ... B
™ Bipolar offset binary: obtained by shifting the xQ of unipolar natural 
binary converter by half-scale R/2: 
1 2
1 2( 2 2 ... 2 )
B
Q B
R Rx R b b b Qm− − −= + + + − = −
2 2
™ Two’s complement code: obtained from the offset binary code by 
l h f b l b bcomp ementing t e most signi icant it, i.e., rep acing 1 y .
1 2
1 2( 2 2 ... 2 ) 2
B
Q B
Rx R b b b− − −= + + + −
1 11b b= −
9 QuantizationHa H. Kha
2. D/A Converters-Example
™ A 4-bit D/A converter has a full-scale R=10 volts. Find the quantized 
l l f h f llana og va ues or t e o owing cases ?
a) Natural binary with the input bits b=[1001] ? 
b) Offset binary with the input bits b=[1011] ? 
) T ’ l bi i h h i bi b [1101] ?c wo s comp ement nary w t t e nput ts = 
10 QuantizationHa H. Kha
3. A/D converter
™ A/D converters quantize an analog value x so that is is represented 
b B bits b=[b b b ]y 1, 2,, B .
Fig: B-bit A/D converter
11 QuantizationHa H. Kha
3. A/D converter
™One of the most popular converters is the successive approximation 
A/D con erter v
Fig: Successive approximation A/D converter
™ After B tests, the successive approximation register (SAR) will hold 
the correct bit vector b.
12 QuantizationHa H. Kha
3. A/D converter
™ Successive approximation algorithm
where the unit-step function is defined by 1 0( )
0 0
if x
u x
if x
≥⎧= ⎨ <⎩
This algorithm is applied for the natural and offset binary with 
truncation quantization.
13 QuantizationHa H. Kha
3. A/D converter-Example
™ Consider a 4-bit ADC with the full-scale R=10 volts. Using the 
s ccessi e appro imation algorithm to find offset binar ofu v x y 
truncation quantization for the analog values x=3.5 volts and x=-1.5 
volts. 
14 QuantizationHa H. Kha
3. A/D converter
™ For rounding quantization, we 
shift b Q/2
™ For the two’s complement 
code the sign bit b is treated x y : , 1 
separately. 
15 QuantizationHa H. Kha
3. A/D converter-Example
™ Consider a 4-bit ADC with the full-scale R=10 volts. Using the 
s ccessi e appro imation algorithm to find offset and t o’su v x w 
complement of rounding quantization for the analog values x=3.5 
volts . 
16 QuantizationHa H. Kha
Homework
™ Problems 2.1, 2.2, 2.3, 2.5, 2.6
17 QuantizationHa H. Kha