Bài giảng Xử lý tín hiệu số - Chương 2: Các phép biến đổi Fourier - Đặng Quang Hiếu

ET4020 - Xử lý tín hiệu số
Chương 2: Các phép biến đổi Fourier
TS. Đặng Quang Hiếu
Trường Đại học Bách Khoa Hà Nội
Viện Điện tử - Viễn thông
Năm học 2012 - 2013
Outline
Biến đổi Fourier
Chuỗi Fourier rời rạc cho dãy tuần hoàn
Biến đổi Fourier rời rạc
Biến đổi Fourier
n ω
FT
IFT
x(n)
FT−−→ X (ejω) = FT{x(n)} =
∞∑
x=−∞
x(n)e−jωn
◮ Tuần hoàn với chu kỳ 2π
◮ Phổ biên độ: |X (ejω)|, và phổ pha: arg{X (ejω)}.
◮ Biến đổi ngược:
X (ejω)
IFT−−−→ x(n) = IFT{X (ejω)} = 1
2π
∫ pi
−pi
X (ejω)ejωndω
Các ví dụ về FT
1. Tìm X (ejω), |X (ejω)| và arg{X (ejω)} của các dãy sau đây:
(a) x(n) = δ(n)
(b) x(n) = δ(n − 2)
(c) x(n) = δ(n − 2)− δ(n)
(d) x(n) = rectN(n)
(e) x(n) = (0.5)nu(n)
(f) x(n) = u(n)
2. Xét bộ lọc thông thấp lý tưởng có đáp ứng tần số (trong một
chu kỳ) như sau:
Hlp(e
jω) =
{
1, |ω| ≤ ωc
0, ωc < |ω| ≤ π
(a) Hãy tìm đáp ứng xung hlp(n) của bộ lọc này.
(b) Giải bài toán cho trường hợp bộ lọc thông cao
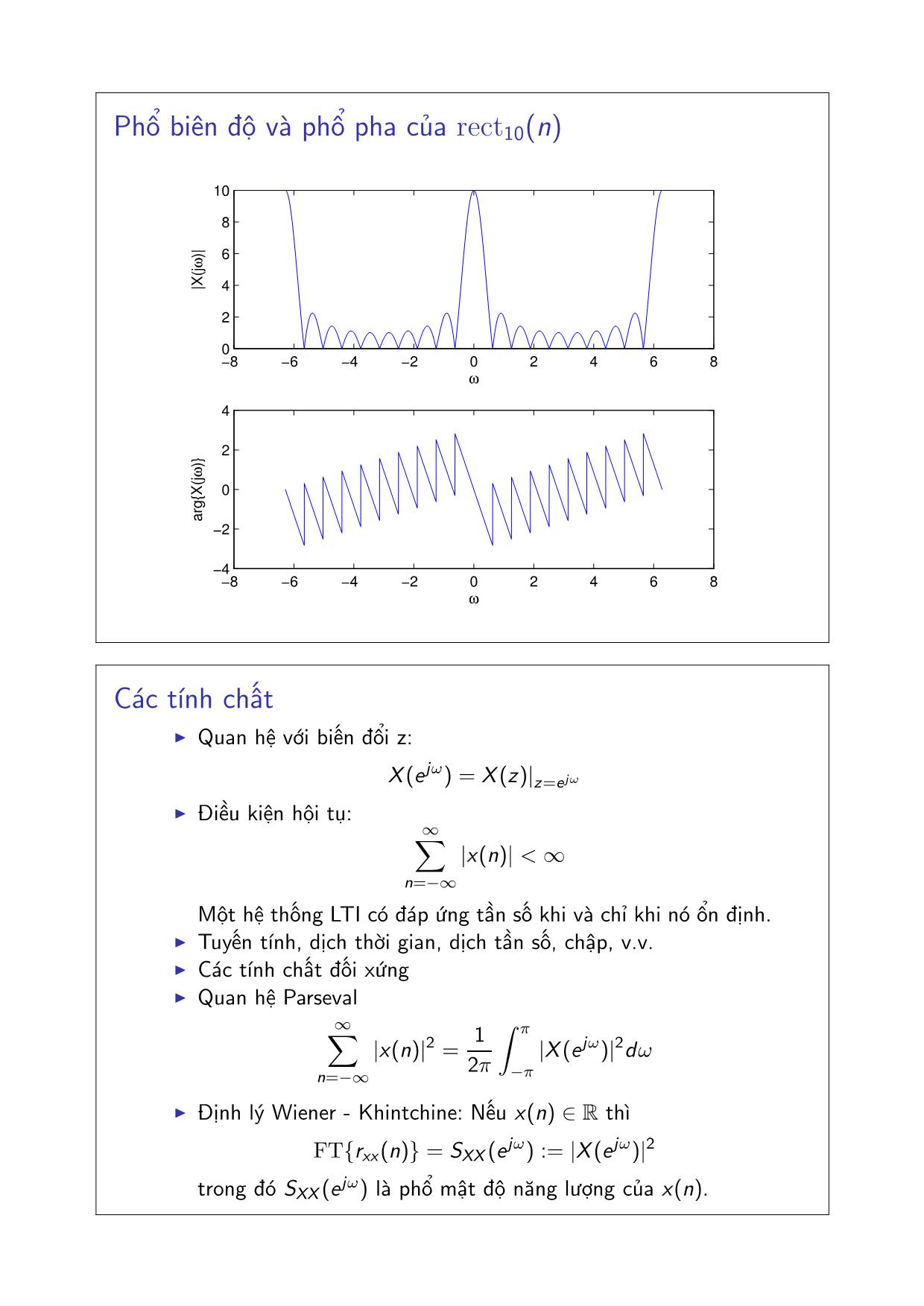
Phổ biên độ và phổ pha của rect10(n)
−8 −6 −4 −2 0 2 4 6 8
0
2
4
6
8
10
ω
|X(
jω)
|
−8 −6 −4 −2 0 2 4 6 8
−4
−2
0
2
4
ω
a
rg
{X
(jω
)}
Các tính chất
◮ Quan hệ với biến đổi z:
X (ejω) = X (z)|z=e jω
◮ Điều kiện hội tụ:
∞∑
n=−∞
|x(n)| <∞
Một hệ thống LTI có đáp ứng tần số khi và chỉ khi nó ổn định.
◮ Tuyến tính, dịch thời gian, dịch tần số, chập, v.v.
◮ Các tính chất đối xứng
◮ Quan hệ Parseval
∞∑
n=−∞
|x(n)|2 = 1
2π
∫ pi
−pi
|X (ejω)|2dω
◮ Định lý Wiener - Khintchine: Nếu x(n) ∈ R thì
FT{rxx(n)} = SXX (ejω) := |X (ejω)|2
trong đó SXX (e
jω) là phổ mật độ năng lượng của x(n).
Outline
Biến đổi Fourier
Chuỗi Fourier rời rạc cho dãy tuần hoàn
Biến đổi Fourier rời rạc
Khái niệm dãy tuần hoàn
x˜(n) = x˜(n − N), ∀n
◮ Chu kỳ N ∈ Z→ ký hiệu x˜(n)N .
◮ Tồn tại khai triển Fourier
◮ Khác hệ số N so với khái niệm chuỗi Fourier cho tín hiệu tuần
hoàn trong môn Tín hiệu và hệ thống!
Định nghĩa cặp chuỗi Fourier rời rạc cho dãy tuần hoàn
X˜ (k) =
N−1∑
n=0
x˜(n)e−j
2pi
N
kn
x˜(n) =
1
N
N−1∑
k=0
X˜ (k)ej
2pi
N
kn
◮ WN = e
−j 2pi
N .
◮ Biên độ và pha: |X˜ (k)|, arg{X˜ (k)}.
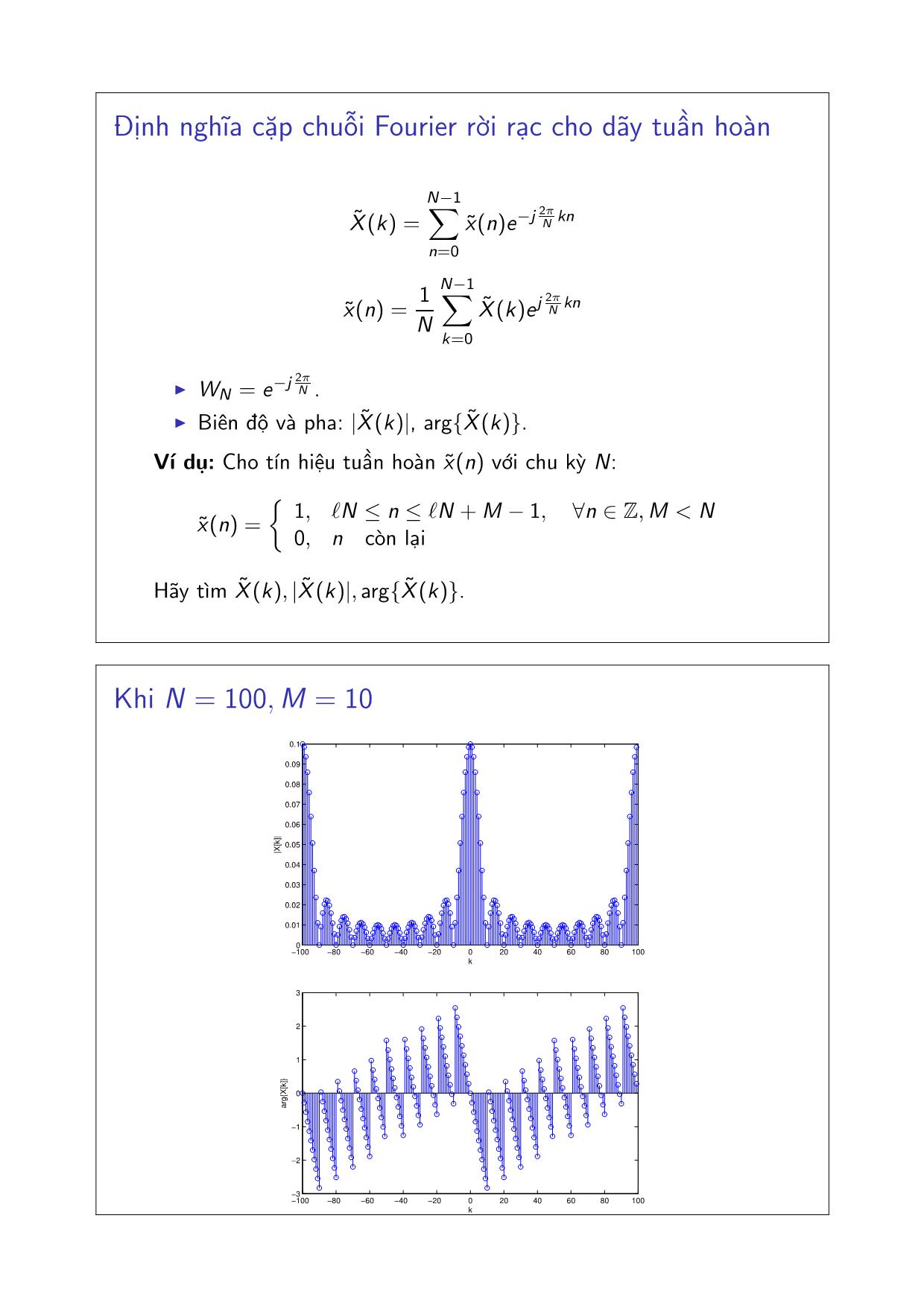
Ví dụ: Cho tín hiệu tuần hoàn x˜(n) với chu kỳ N:
x˜(n) =
{
1, ℓN ≤ n ≤ ℓN +M − 1, ∀n ∈ Z,M < N
0, n còn lại
Hãy tìm X˜ (k), |X˜ (k)|, arg{X˜ (k)}.
Khi N = 100,M = 10
−100 −80 −60 −40 −20 0 20 40 60 80 100
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
k
|X[
k]|
−100 −80 −60 −40 −20 0 20 40 60 80 100
−3
−2
−1
0
1
2
3
k
a
rg
{X
[k]
}
Các tính chất
◮ Tuyến tính, dịch thời gian, dịch tần số
◮ Đối ngẫu: Nếu
x˜(n)
DFS←−−→ X˜ (k)
thì
X˜ (n)
DFS←−−→ Nx˜(−k)
◮ Các tính chất đối xứng
Chập tuần hoàn
x˜1(n)
DFS←−−→ X˜1(k)
x˜2(n)
DFS←−−→ X˜2(k)
Nếu X˜3(k) = X˜1(k)X˜2(k)
−→ Chập tuần hoàn:
x˜3(n)N = x˜1(n)(∗˜)N x˜2(n) =
N−1∑
m=0
x˜1(m)x˜2(n −m)
Các bước tính chập tuần hoàn
Tìm x˜3(n0), ∀n0 ∈ [0, (N − 1)]
(1) Lấy đối xứng x˜2(m)→ x˜2(−m)
(2) Dịch theo trục thời gian đi n0 mẫu
(3) Nhân: v˜n0(m) = x˜1(m)x˜2(n0 −m) trong đoạn [0, (N − 1)]
(4) Tính tổng: Cộng tất cả thành phần khác không của v˜n0(m)
trong đoạn [0, (N − 1)] → x˜3(n0)
(5) Kết quả là một dãy tuần hoàn với chu kỳ N:
x˜3(n0) = x˜3(n0 + rn), ∀r ∈ Z.
Minh họa các bước tính phép chập tuần hoàn
0 1 2 3 4 5 6-1-2-3-4
b b b
b
b b b
b
b b b
m
x˜1(m)
0 1 2 3 4 5 6-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
m
x˜2(m)
0 1 2 3 4 5 6-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
m
x˜2(−m)
0 1 2 3 4 5 6-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
m
v˜0(m) x˜3(0) = 1.75
0 1 2 3 4 5 6-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
m
x˜2(1 −m)
0 1 2 3 4 5 6-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
m
v˜1(m) x˜3(1) = 2
0 1 2 3 4 5 6-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
m
x˜2(2 −m)
0 1 2 3 4 5 6-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
m
v˜2(m) x˜3(2) = 2.25
Kết quả phép chập tuần hoàn
0 1 2 3 4 5 6 7 8-1-2-3-4
b b b
b
b b b
b
b b b
b
b
n
x˜1(n)
0 1 2 3 4 5 6 7 8-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
b
b
n
x˜2(n)
0 1 2 3 4 5 6 7 8-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
b
b
n
x˜3(n)
Bài tập
1. Viết chương trình Matlab để vẽ phổ biên độ và phổ pha của
một dãy có chiều dài hữu hạn bất kỳ
2. Sử dụng hàm freqz trong Matlab để vẽ đáp ứng tần số của
một hệ thống LTI từ phương trình sai phân tuyến tính hệ số
hằng.
3. Lấy mẫu tần số. Cho dãy x(n) có chiều dài hữu hạn L với phổ
X (ejω) (chu kỳ 2π). Để biểu diễn phổ tín hiệu, người ta lấy
các mẫu tại tần số ω = k 2piN để thu được X (e
jk 2pi
N ) với chu kỳ
lấy mẫu 2piN . Với những giá trị nào của N thì ta có thể tái tạo
lại hoàn toàn x(n) từ các mẫu X (ejk
2pi
N )?
Outline
Biến đổi Fourier
Chuỗi Fourier rời rạc cho dãy tuần hoàn
Biến đổi Fourier rời rạc
Khái niệm
Xét tín hiệu x(n) có chiều dài hữu hạn N, nếu lấy đủ
mẫu (tối thiểu N / một chu kỳ) của phổ X (ejω), thì có
thể khôi phục lại được x(n).
−→ Biến đổi Fourier rời rạc DFT cho dãy có chiều dài
hữu hạn!
Cho x(n) với chiều dài hữu hạn N: x(n) = 0, ∀n N − 1,
ta có dãy tuần hoàn x˜(n):
x˜(n) = x(n mod N)
Lấy một chu kỳ từ DFS{X˜ (k)}:
X (k) =
{
X˜ (k), 0 ≤ k ≤ (N − 1)
0, k còn lại
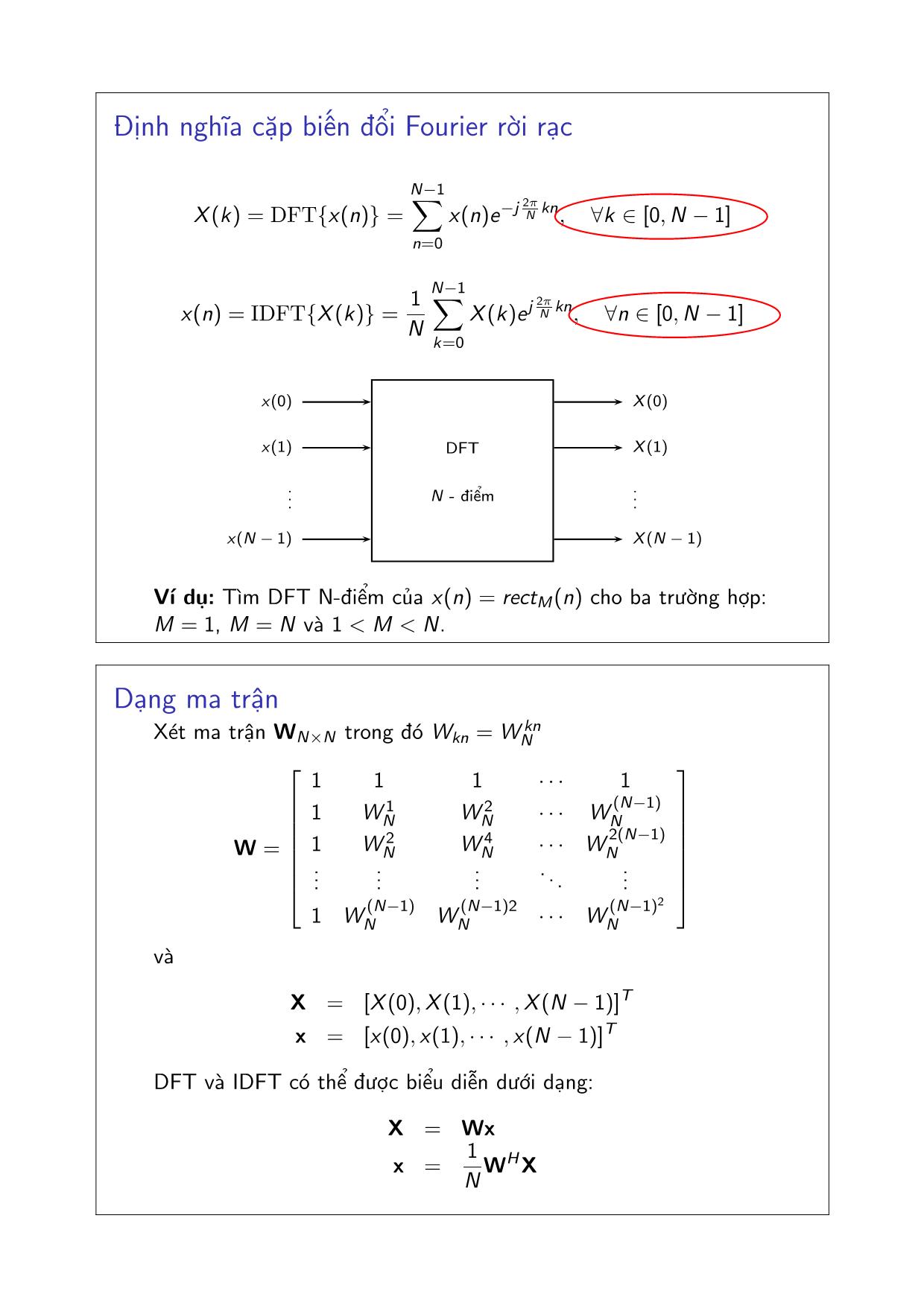
Định nghĩa cặp biến đổi Fourier rời rạc
X (k) = DFT{x(n)} =
N−1∑
n=0
x(n)e−j
2pi
N
kn, ∀k ∈ [0,N − 1]
x(n) = IDFT{X (k)} = 1
N
N−1∑
k=0
X (k)ej
2pi
N
kn, ∀n ∈ [0,N − 1]
DFT
N - điểm
x(0)
x(1)
x(N − 1)
...
X (0)
X (1)
X (N − 1)
...
Ví dụ: Tìm DFT N-điểm của x(n) = rectM(n) cho ba trường hợp:
M = 1, M = N và 1 < M < N.
Dạng ma trận
Xét ma trận WN×N trong đó Wkn = W knN
W =

1 1 1 · · · 1
1 W 1N W
2
N · · · W (N−1)N
1 W 2N W
4
N · · · W 2(N−1)N
...
...
...
. . .
...
1 W
(N−1)
N W
(N−1)2
N · · · W (N−1)
2
N

và
X = [X (0),X (1), · · · ,X (N − 1)]T
x = [x(0), x(1), · · · , x(N − 1)]T
DFT và IDFT có thể được biểu diễn dưới dạng:
X = Wx
x =
1
N
WHX
Dịch vòng: Một chu kỳ của tín hiệu tuần hoàn sau dịch
0 1 2 3 4 5 6 7 8-1-2-3-4
b
b
b
b
n
x(n)
0 1 2 3 4 5 6 7 8-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
b
b
n
x˜(n)N
0 1 2 3 4 5 6 7 8-1-2-3-4
b
b
b
b
b
b
b
b
b
b
b
b
b n
x˜(n − n0)N
0 1 2 3 4 5 6 7 8-1-2-3-4
b
b
b
b
n
x(n − n0)N
Dịch vòng: Đặt lên một vòng tròn và quay quanh tâm
a
b
c
d
a
b
c
dx(n)N = {a, b, c, d} x(n− 1)N = {d, a, b, c}
Tính chất dịch
◮ Dịch thời gian
DFT{x(n − n0)N} = e−j(2pi/N)kn0X (k)
◮ Dịch tần số
DFT{ej(2pi/N)k0nx(n)} = X (k − k0)N
Đối ngẫu
Nếu
DFT{x(n)} = X (k)
thì
DFT{X (n)} = Nx(−k)N
Lưu ý: x(−k)N =?
Đảo trục thời gian
Nếu
DFT{x(n)} = X (k)
thì
DFT{x(−n)N} = X (−k)N
Các tính chất đối xứng
(a) DFT{x∗(n)} = X ∗(−k)N
(b) DFT{x∗(−n)N} = X ∗(k)
(c) DFT{Re[x(n)]} = 12 [X (k) + X ∗(−k)N ]
(d) DFT{12 [x(n) + x∗(−n)N ]} = Re[X (k)]
(e) Nếu x(n) ∈ R
◮ X (k) = X ∗(−k)N = X ∗(N − k)
◮ Re[X (k)] = Re[X (N − k)]
◮ Im[X (k)] = −Im[X (N − k)]
◮ |X (k)| = |X (N − k)|
◮ arg{X (k)} = − arg{X (N − k)}
Chập vòng
Định nghĩa chập vòng:
x3(n)N = x1(n)(∗)Nx2(n) =
N−1∑
m=0
x1(m)x2(n−m)N , ∀n ∈ [0,N−1]
Áp dụng DFT ta có:
DFT{x1(n)(∗)Nx2(n)} = X1(k)X2(k)
Cách tính chập vòng:
◮ Miền thời gian
◮ Miền tần số
Ví dụ: Tính chập vòng 5-điểm (N = 5) của hai dãy sau:
x1(n) = rect4(n) + 0.5δ(n − 4)
x2(n) =
{
1− n4 , 0 ≤ n ≤ 4
0, n còn lại
Dạng ma trận của chập vòng
x3 = X2 · x1
trong đó x3 = [x3(0), x3(1), · · · , x3(N − 1)]T ,
x1 = [x1(0), x1(1), · · · , x1(N − 1)]T và X2 là (circulant matrix):
X2 =

x2(0) x2(N − 1) · · · x2(1)
x2(1) x2(0) · · · x2(2)
...
...
. . .
...
x2(N − 1) x2(N − 2) · · · x2(0)

◮ Dạng ma trận của chập tuyến tính → ma trận Toeplitz!
◮ Làm thế nào để tính chập vòng bằng Matlab?
Mối quan hệ giữa chập vòng và chập tuyến tính
Cho hai dãy có chiều dài hữu hạn, x(n): [0 · · · (N − 1)] và h(n):
[0 · · · (M − 1)]. Nếu
y1(n) = x(n) ∗ h(n)
và
y2(n) = x(n)(∗)Lh(n)
(a) Với những giá trị nào của L thì y1(n) = y2(n), ∀n?
(b) Nếu L = N thì tại những thời điểm n nào ta có y1(n) = y2(n)?
Quan hệ Parseval
N−1∑
n=0
x(n)y∗(n) =
1
N
N−1∑
k=0
X (k)Y ∗(k)
Nếu x(n) = y(n):
N−1∑
n=0
|x(n)|2 = 1
N
N−1∑
k=0
|X (k)|2