Bài giảng Xử lý tín hiệu số - Chương 1: Tín hiệu và hệ thống rời rạc - Đặng Quang Hiếu

ET4020 - Xử lý tín hiệu số
Chương 1: Tín hiệu và hệ thống rời rạc
TS. Đặng Quang Hiếu
Trường Đại học Bách Khoa Hà Nội
Viện Điện tử - Viễn thông
Năm học 2012 - 2013
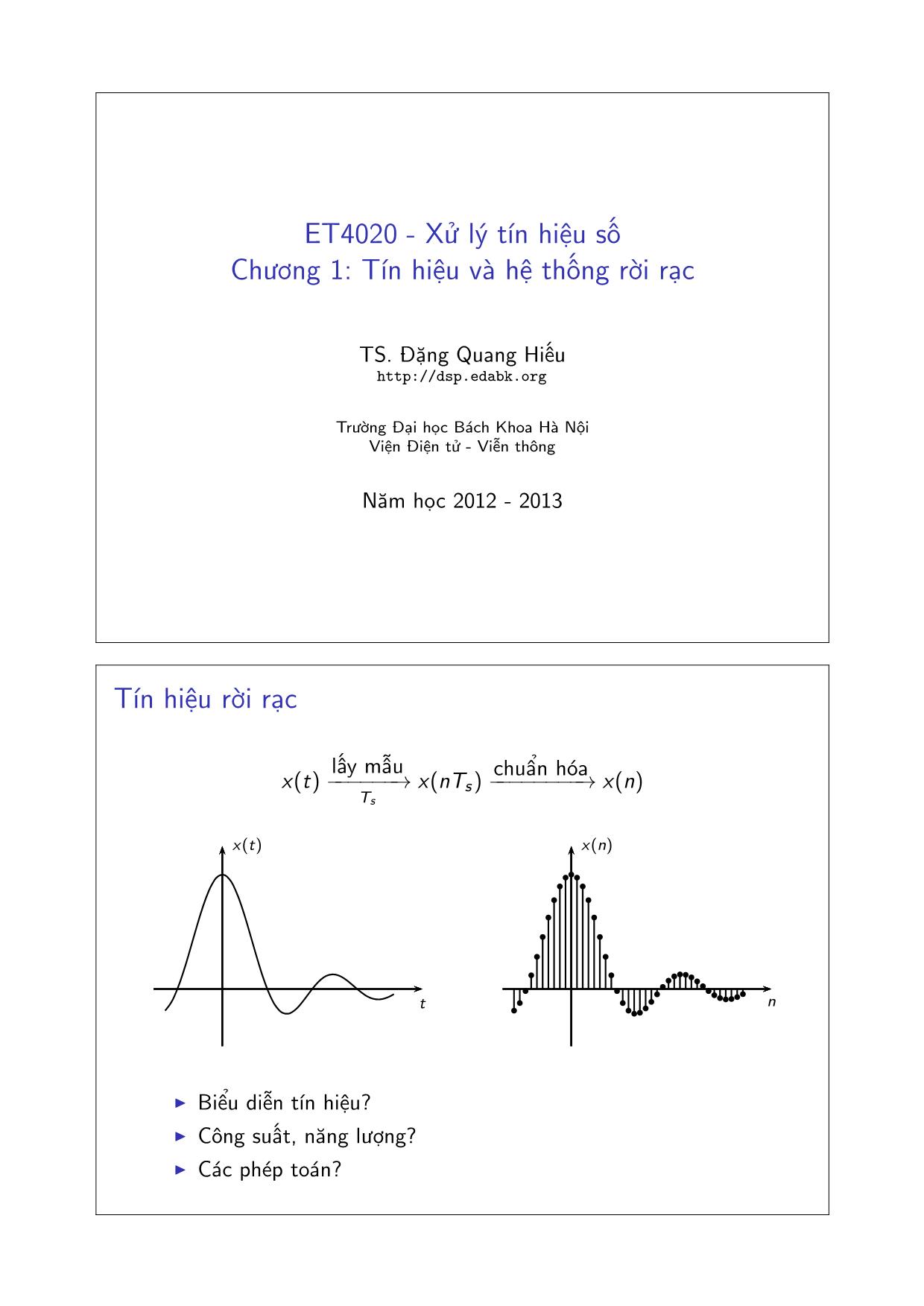
Tín hiệu rời rạc
x(t)
lấy mẫu−−−−−−→
Ts
x(nTs)
chuẩn hóa−−−−−−−−→ x(n)
t
x(t)
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
n
x(n)
◮ Biểu diễn tín hiệu?
◮ Công suất, năng lượng?
◮ Các phép toán?
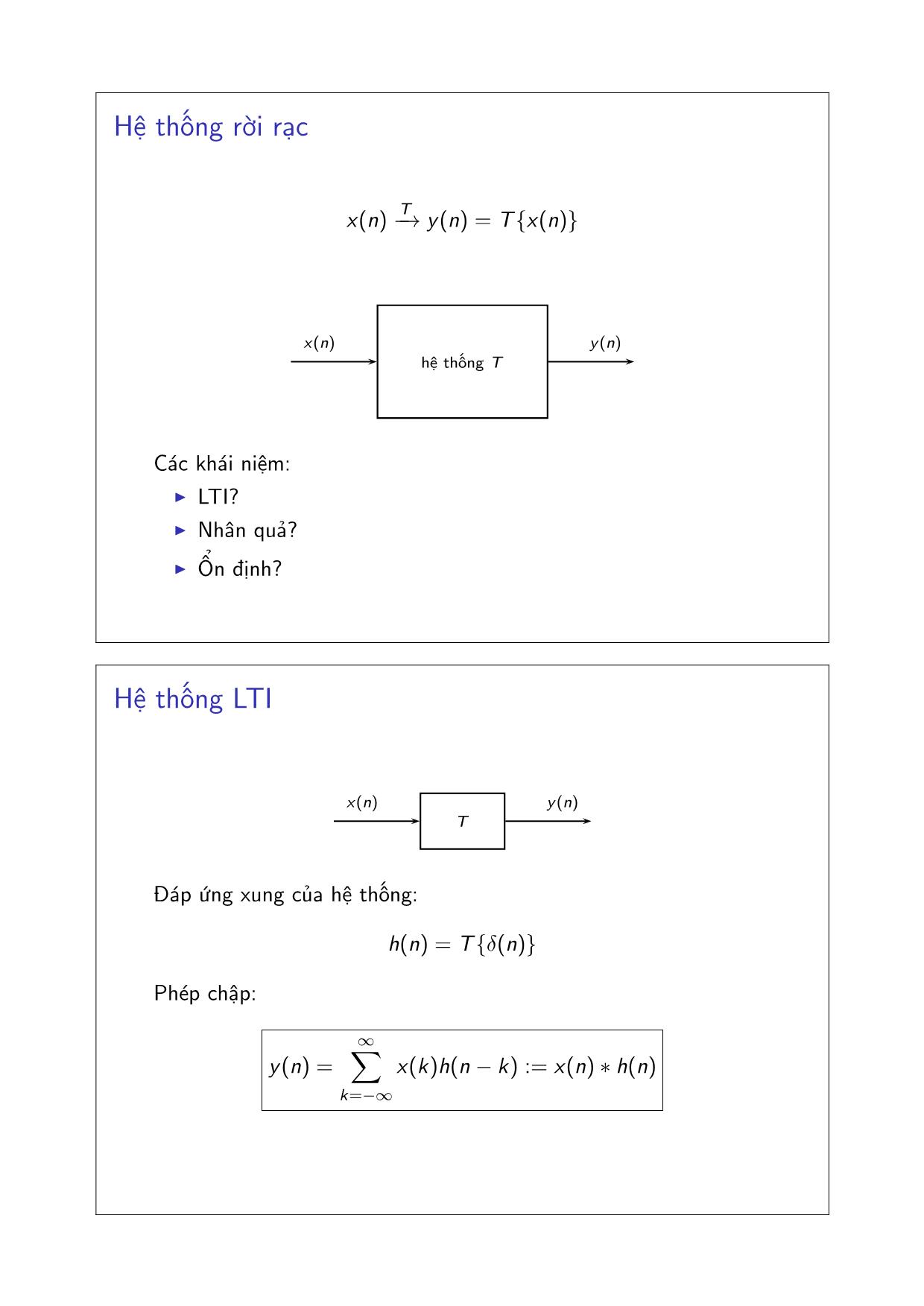
Hệ thống rời rạc
x(n)
T−→ y(n) = T{x(n)}
x(n) y(n)
hệ thống T
Các khái niệm:
◮ LTI?
◮ Nhân quả?
◮ Ổn định?
Hệ thống LTI
x(n) y(n)
T
Đáp ứng xung của hệ thống:
h(n) = T{δ(n)}
Phép chập:
y(n) =
∞∑
k=−∞
x(k)h(n − k) := x(n) ∗ h(n)
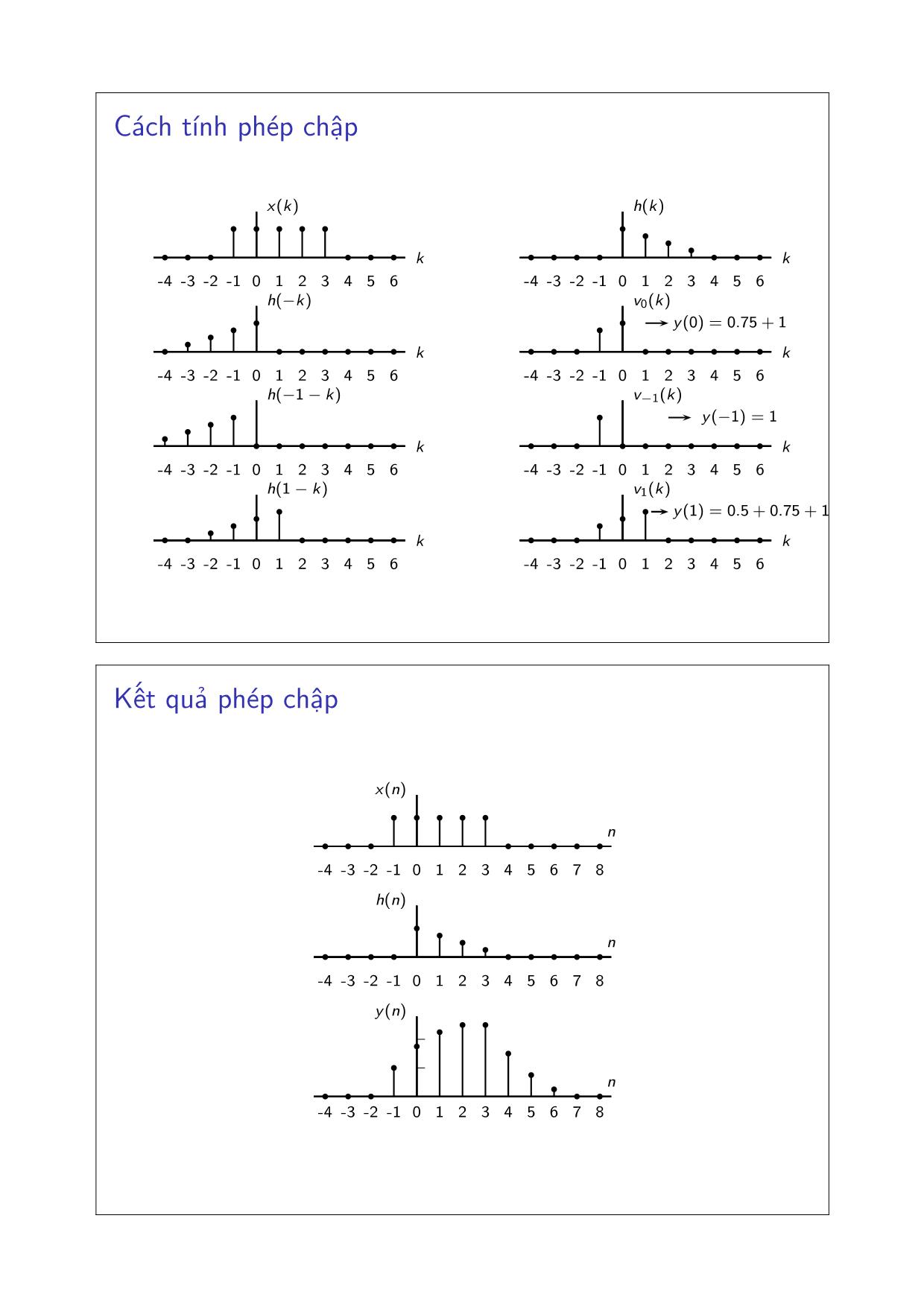
Cách tính phép chập
0 1 2 3 4 5 6-1-2-3-4
b b b
b b b b b
b b b k
x(k)
0 1 2 3 4 5 6-1-2-3-4
b b b b
b
b
b
b
b b b k
h(k)
0 1 2 3 4 5 6-1-2-3-4
b
b
b
b
b
b b b b b b k
h(−k)
0 1 2 3 4 5 6-1-2-3-4
b b b
b
b
b b b b b b k
v0(k)
y(0) = 0.75+ 1
0 1 2 3 4 5 6-1-2-3-4
b
b
b
b
b b b b b b b k
h(−1 − k)
0 1 2 3 4 5 6-1-2-3-4
b b b
b
b b b b b b b k
v−1(k)
y(−1) = 1
0 1 2 3 4 5 6-1-2-3-4
b b
b
b
b
b
b b b b b k
h(1 − k)
0 1 2 3 4 5 6-1-2-3-4
b b b
b
b
b
b b b b b k
v1(k)
y(1) = 0.5+ 0.75+ 1
Kết quả phép chập
0 1 2 3 4 5 6 7 8-1-2-3-4
b b b
b b b b b
b b b b b
n
x(n)
0 1 2 3 4 5 6 7 8-1-2-3-4
b b b b
b
b
b
b
b b b b b
n
h(n)
0 1 2 3 4 5 6 7 8-1-2-3-4
b b b
b
b
b
b b
b
b
b
b b
n
y(n)
Các tính chất của phép chập
◮ Giao hoán
◮ Kết hợp
◮ Phân phối
◮ Ghép nối hệ thống?
Hệ thống LTI nhân quả, ổn định
Xét hệ thống LTI với đáp ứng xung h(n).
◮ Hệ thống ổn định:
∞∑
n=−∞
|h(n)| <∞
◮ Hệ thống nhân quả:
h(n) = 0, ∀n < 0
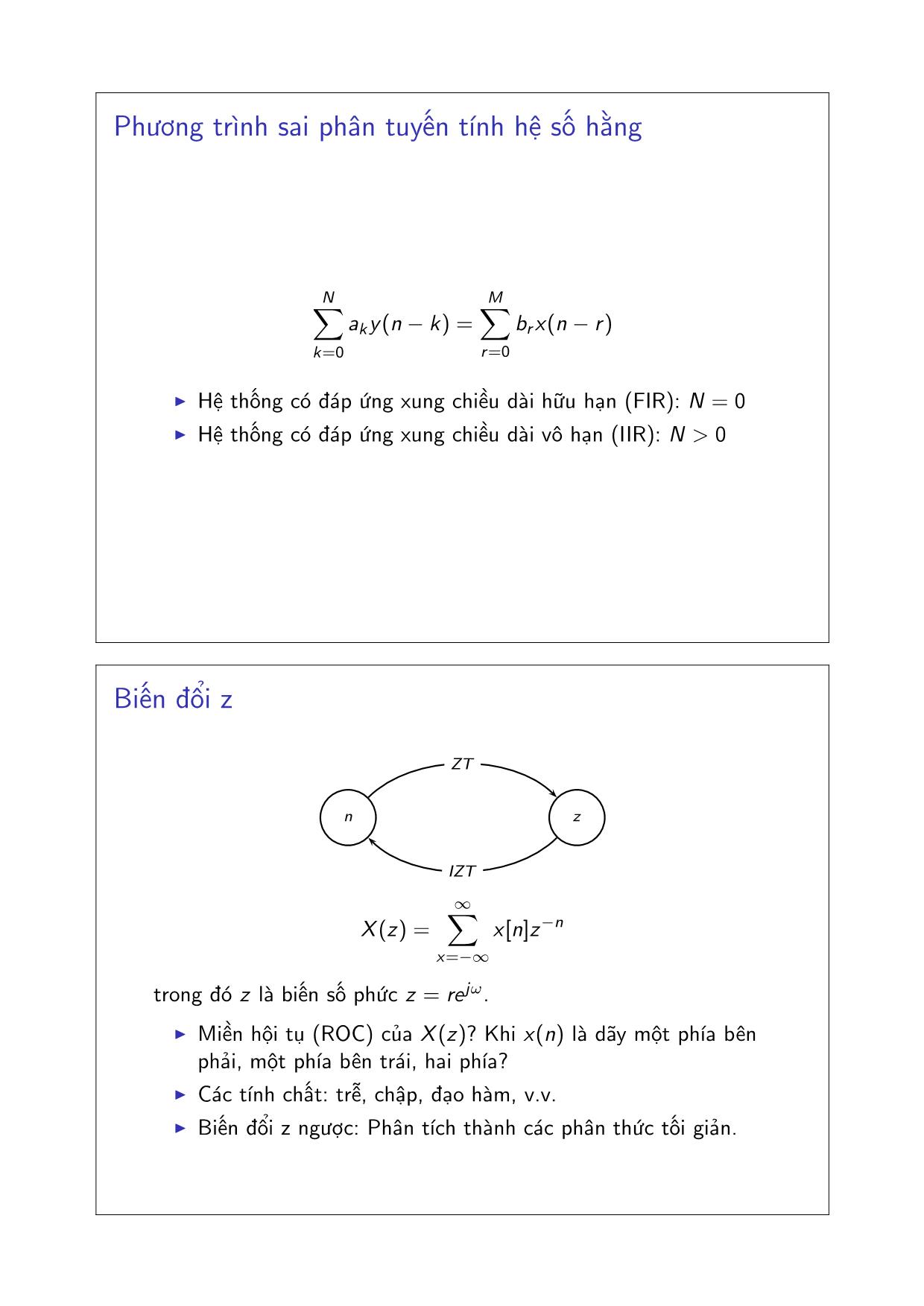
Phương trình sai phân tuyến tính hệ số hằng
N∑
k=0
aky(n − k) =
M∑
r=0
brx(n − r)
◮ Hệ thống có đáp ứng xung chiều dài hữu hạn (FIR): N = 0
◮ Hệ thống có đáp ứng xung chiều dài vô hạn (IIR): N > 0
Biến đổi z
n z
ZT
IZT
X (z) =
∞∑
x=−∞
x [n]z−n
trong đó z là biến số phức z = rejω.
◮ Miền hội tụ (ROC) của X (z)? Khi x(n) là dãy một phía bên
phải, một phía bên trái, hai phía?
◮ Các tính chất: trễ, chập, đạo hàm, v.v.
◮ Biến đổi z ngược: Phân tích thành các phân thức tối giản.
Hàm truyền đạt
H(z) = ZT{x(n)}
◮ Các điểm cực zpk và các điểm không z0r? Vẽ trên mặt phẳng
phức?
◮ Hệ thống LTI nhân quả ổn định:
|zpk | < 1, ∀k
◮ Sử dụng biến đổi z một phía để giải phương trình sai phân
tuyến tính hệ số hằng
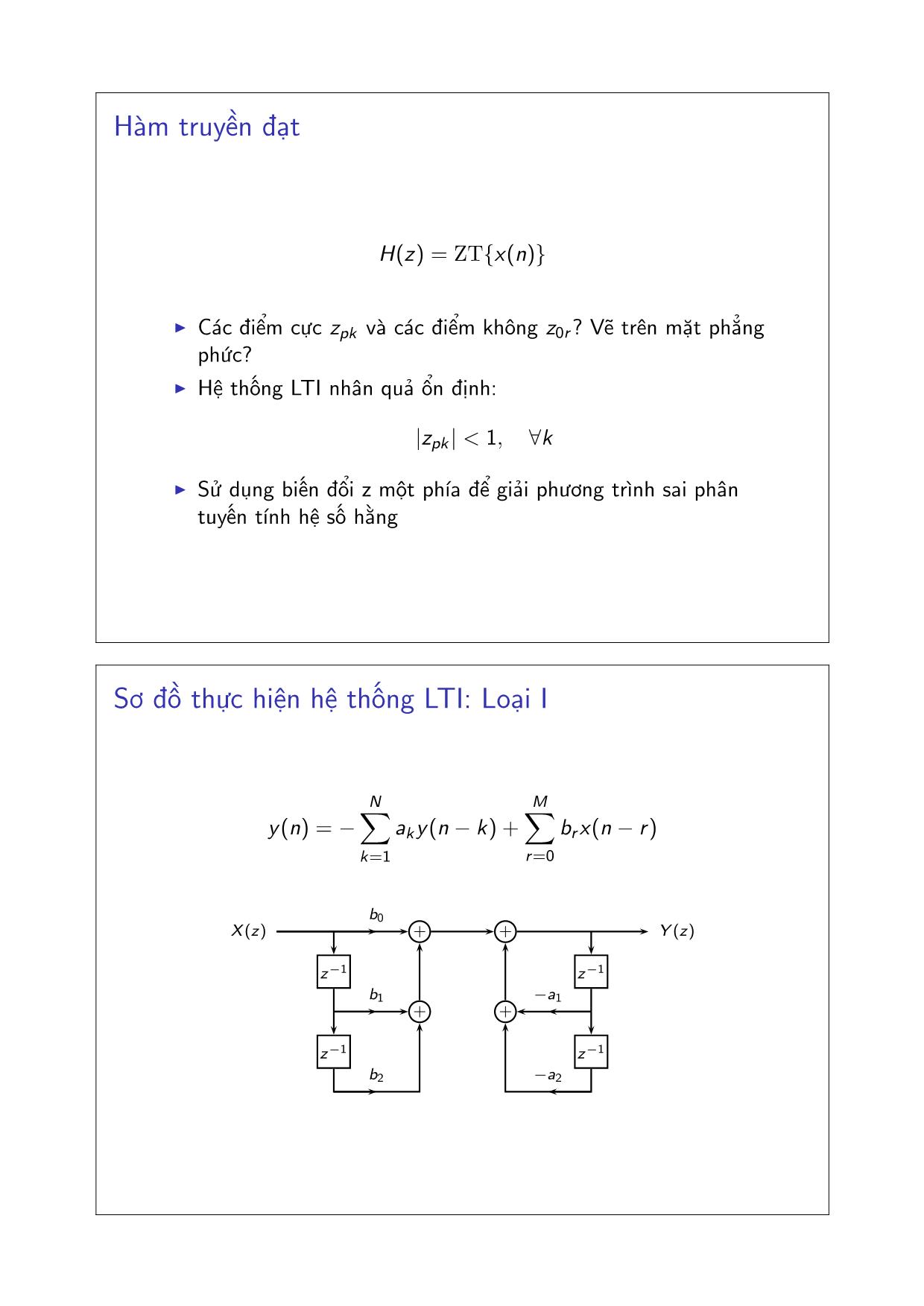
Sơ đồ thực hiện hệ thống LTI: Loại I
y(n) = −
N∑
k=1
aky(n − k) +
M∑
r=0
brx(n − r)
X (z) Y (z)
b0
b1
b2
+
+
+
+
z−1
z−1
z−1
z−1
−a1
−a2
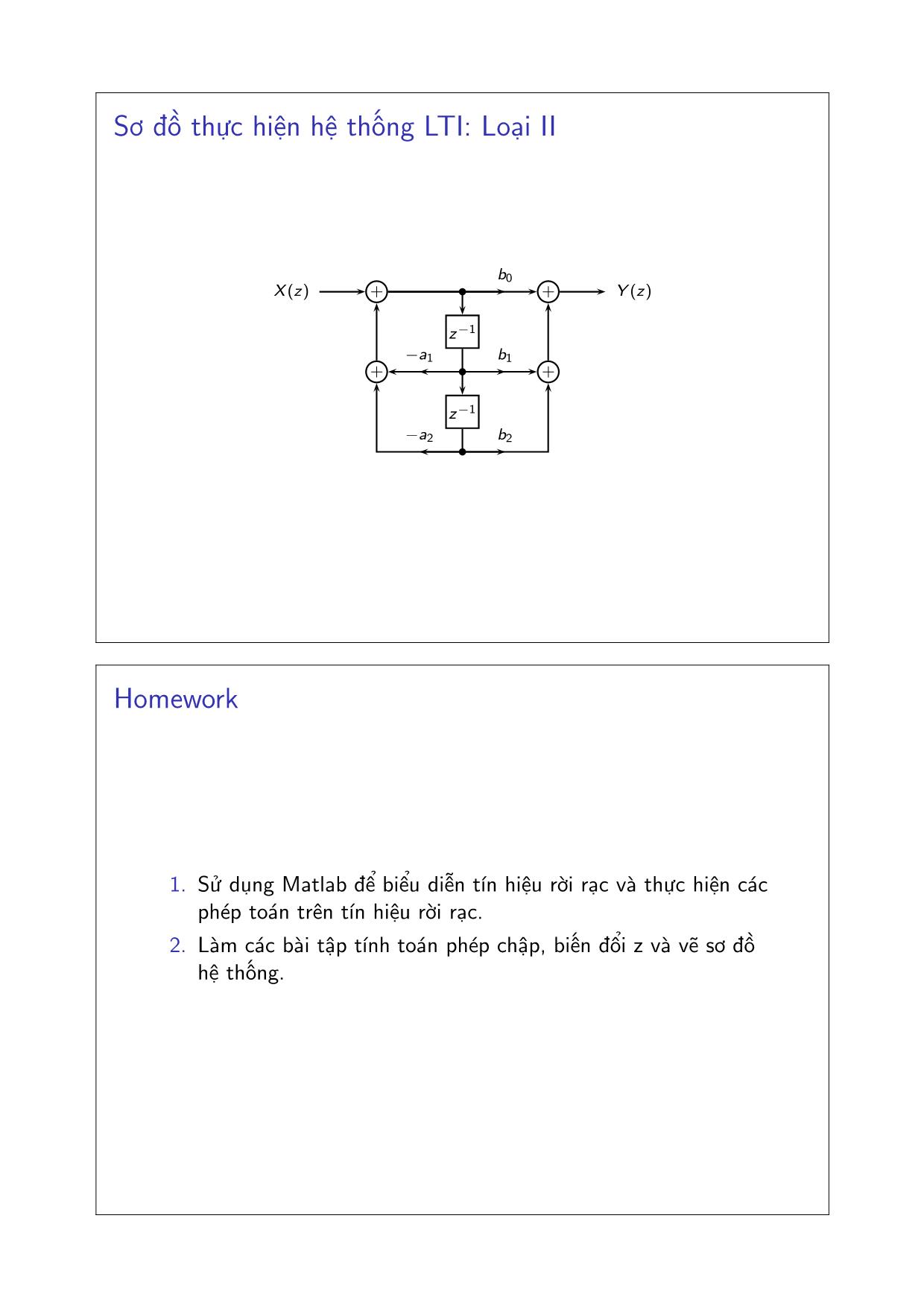
Sơ đồ thực hiện hệ thống LTI: Loại II
b
b
b
X (z) Y (z)
b0
b1
b2
+
+
+
+
z−1
z−1
−a1
−a2
Homework
1. Sử dụng Matlab để biểu diễn tín hiệu rời rạc và thực hiện các
phép toán trên tín hiệu rời rạc.
2. Làm các bài tập tính toán phép chập, biến đổi z và vẽ sơ đồ
hệ thống.