Bài giảng Xử lý tín hiệu số (Bản hay)
Những nội dung cần nắm vững:
Chương 1
• Các tín hiệu rời rạc đặc biệt (xung đơn vị, bậc đơn vị, hàm mũ, tuần
hoàn)
• Các phép toán với tín hiệu rời rạc (nhân với hệ số, cộng, phép dịch)
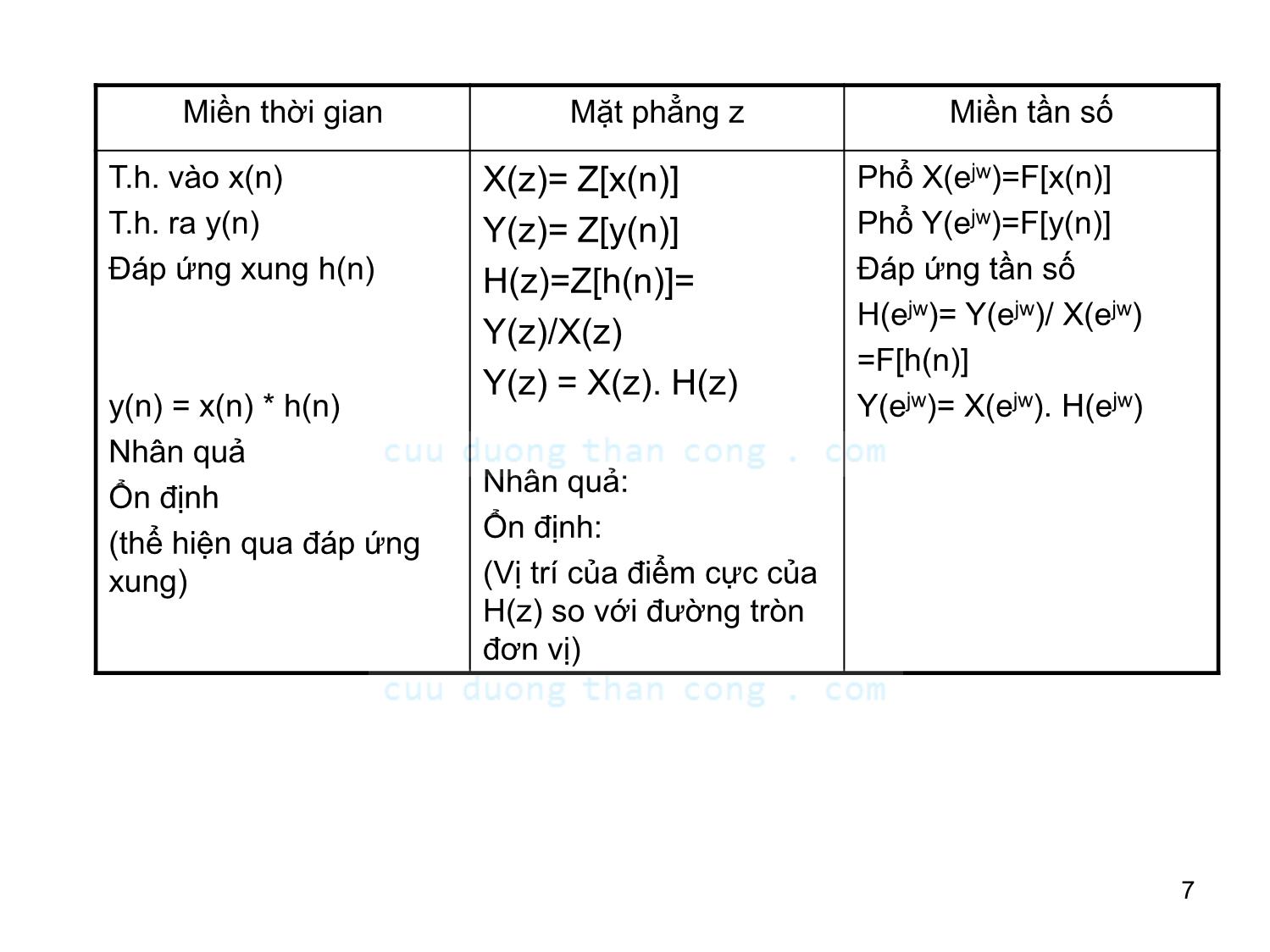
• Quan hệ vào-ra với hệ TT-BB:
– Tín hiệu vào (tác động), tín hiệu ra (đáp ứng), đáp ứng xung
– Cách tính tổng chập y(n) = x(n) * h(n)
• Các tính chất của hệ TT-BB
– nhân quả, ổn định
• Quan hệ vào-ra thông qua PT-SP-TT-HSH
• Hệ TT-BB xét trong miền tần số:
– Đáp ứng tần số (đáp ứng biên độ, đáp ứng pha)
– Phổ tín hiệu (phổ biên độ, phổ pha)5
Những nội dung cần nắm vững:
Chương 2
• Định nghĩa biến đổi z (1 phía, 2 phía)
• Miền hội tụ của biến đổi z
• Các tính chất của biến đổi z
• Phương pháp tính biến đổi z ngược (phân tích thành các phân
thức hữu tỉ đơn giản )
• Cách tra cứu bảng công thức biến đổi z
• Ứng dụng biến đổi z 1 phía để giải PT-SP
• Xét tính nhân quả và ổn định thông qua hàm truyền đạt H(z)

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Xử lý tín hiệu số (Bản hay)

X ( z ) k azk k0 Biểu diễn H(z) qua các điểm không zr và các điểm cực pk: M ( z zr ) H ( z ) H r1 0 N ( z pk ) k1 100 Bài tập chương 2 (1/2) 1. Cho tín hiệu 1 0 n N -1 x (n ) 0 n cßn l¹ i Hãy tính biến đổi z của tín hiệu này bằng cách dùng: a) Định nghĩa biến đổi z b) Tín hiệu u(n) và trễ của u(n) 1 1 2. Tính biến đổi z ngược của X ( z ) ln 1 z với |z|>1/2 2 3. Ứng dụng biến đổi z 1 phía để giải PT-SP: y(n)-(1/2) y(n-1)=x(n)-(1/2) x(n-1) Biết x(n) = (n), y(-1)=0. 101 Bài tập chương 2 (2/2) 4. Hệ TT-BB có PT-SP: y(n)=y(n-1)+y(n-2)+x(n-1) a) Xác định hàm truyền đạt, điểm không, điểm cực b) Nhận xét tính nhân quả, ổn định c) Xác định đáp ứng xung sao cho hệ nhân quả 102 Giải bài tập chương 2 (1/5) 1. Tín hiệu x(n): 1 -5 -4 -3 -2 -1 0 1 2 3 N-1 N n N1 N n 1z a) X (z ) 1 .z 1 n0 1z b) x(n) u(n) u(n N) N 1z ZZZx(n) u(n) u(n N) 11 1 z 1 z 103 Giải bài tập chương 2 (2/5) 2. 21 dX(z) (1/2)z 1 z zz 11 d z1 (1/2)z 2 1 (1/2)z n 1 n 1 1 1 1 1 x(n) u(n1) u(n1) n 2 2 n 2 3. Biến đổi z 1 phía cả 2 vế của PT-SP: Y(z) (1/2)[z11 Y(z) y( 1)] X(z) (1/2)[z X(z) x( 1)] y(-1) = 0, x(-1)=0, X(z) = 1 Y(z) = 1 y(n)= (n) 104 Giải bài tập chương 2 (3/5) 4. y(n)=y(n-1)+y(n-2)+x(n-1) a) Biến đổi z cả 2 vế: Y(z)=z-1Y(z)+z-2Y(z)+z-1X(z) 1 Y (z ) z z H(z ) 1 2 2 X (z ) 1 z z z z 1 Nghiệm mẫu số: 1 1 4 z1 ,2 1,62 và -0,62 2 Hệ có 1 điểm không tại z=0 và 2 điểm cực tại z=1,62;z=-0,62 105 Giải bài tập chương 2 (4/5) 4. Im(z) b) 1 Re(z) z=-0,62 z=1,62 0 |z| 0,62 :Không nhân quả, không ổn định 0,62 |z| 1,62 :Không nhân quả, ổn định |z|>1,62 : Nhân quả, không ổn định 106 Giải bài tập chương 2 (5/5) 4. c) 1 H(z) z.H (z) H (z) 112 z z 1 1 A12 A H1 (z ) (z 1,62)(z 0,62) z 1,62 z 0,62 1 A(z1,62)1 0,45 (z 1,62)(z 0,62) z 1 ,6 2 1 A(z0,62)2 0,45 (z 1,62)(z 0,62) z 0 ,6 2 0 , 4 5 0 , 4 5 H(z ) 11 1 1,62z 1 0,62z nn h(n) 0,45 (1,62) ( 0,62) u(n) 107 S = a0 + a1 + a2 + a3 + + aN-1 ai = ai-1.q N S = a0.(1-q )/(1-q) S = a0 + a1 + a2 + a3 + + aN-1+ ai = ai-1.q S = a0./(1-q) 108 Chương 3 BỘ LỌC SỐ 109 3.1. Khái niệm Trong nhiều ứng dụng khác nhau, ta thường phải thay đổi biên độ của các thành phần tần số khác nhau của tín hiệu hoặc loại bỏ đi một số thành phần tần số nào đó. Quá trình xử lý như vậy đối với tín hiệu được gọi là lọc. Bộ lọc số: là bộ lọc dùng để lọc tín hiệu số Có thể dùng bộ lọc tương tự để lọc tín hiệu số được không ? L 10010010 R 110 3.1. Khái niệm Xét hệ TT-BB có PT-SP 1 y(n) (x(n) x(n 1)) 2 1 Đáp ứng xung của hệ: h(n) (n) (n 1) 2 Đáp ứng tần số của hệ: j1 j j / 2 H(e) 1e e cos /2 2 |H( )| j 1 H(e ) cos( /2) Đáp ứng biên độ của bộ lọc thông thấp 0 /2 111 3.2. Bộ lọc FIR Bộ lọc FIR và IIR NMN=0: FIR ay(nkk k) bx(n k) k 0 k 0 N>0: IIR MMb k y(n) x(n k) h(k)x(n k) N=0 a k 00 k 0 M=1 y(n)=h(0)x(n)+h(1)x(n-1) h(0) x(n) y(n) Sơ đồ khối D x(n-1) h(1) 112 3.2. Bộ lọc FIR const h0 = 0.5; h1 = 0.5; var xn, xnt1, yn: real; begin xnt1 := 0; repeat (* NhËp tÝn hiÖu vµo tõ bµn phÝm *) write(’NhËp tÝn hiÖu vµo xn = ’); readln(xn); (* TÝnh tÝn hiÖu ra *) yn:= h0 * xn + h1 * xnt1; (* TrÔ tÝn hiÖu *) xnt1 := xn; until Ketthuc; end. 113 3.2. Bộ lọc FIR Trường hợp tổng quát h(0) x(n) y(n) D h(1) x(n-1) D h(2) x(n-2) D h(M) x(n-M) 114 3.3. Bộ lọc IIR Hệ bậc nhất a0y(n)+a1y(n-1)=b0x(n) Giả thiết a0 = 1 y(n)=-a1y(n-1)+b0x(n) b0 x(n) y(n) D y(n-1) -a1 115 3.3. Bộ lọc IIR Hệ bậc hai a0y(n)+a1y(n-1)=b0x(n)+b1x(n-1) Giả thiết a0 = 1 y(n)=-a1y(n-1)+b0x(n)+ b1x(n-1) =-a1y(n-1) + w(n) w(n)=b0x(n)+b1x(n-1) b0 w(n) x(n) y(n) D D b 1 y(n-1) -a1 116 3.3. Bộ lọc IIR MN y(n) bx(n k) ay(n k) Tổng quát (a0 = 1) kk k 0 k 1 N w (n ) ak y (n k ) k1 M w (n ) bk x (n k ) k0 117 3.3. Bộ lọc IIR b0 w(n) x(n) y(n) D D b1 -a1 Dạng trực D D tiếp 1 b2 -a2 D D bM -aN 118 3.3. Bộ lọc IIR Hệ 1 Hệ 2 x(n) w(n) y(n) Hệ 2 Hệ 1 x(n) z(n) y(n) 119 3.3. Bộ lọc IIR z(n) b0 x(n) y(n) D D -a1 b1 D D -a2 b2 D D -aN bM 120 3.3. Bộ lọc IIR z(n) b0 x(n) y(n) D -a1 b1 Dạng M>N trực D -a tiếp 2 2 b2 (chuẩn tắc) D -a N bN D bM 121 3.4. Mắc nối tiếp và song song các hệ H(z) của hệ phức tạp thường được phân tích thành tổng hoặc tích H(z) của các hệ đơn giản, tương ứng với việc mắc song song hoặc nối tiếp các hệ đơn giản Mắc nối tiếp P H (z ) C Hk (z ) C: Hằng số k1 C H1(z) H2(z) HP(z) x(n) y(n) 122 3.4. Mắc nối tiếp và song song các hệ Mắc song song Q H(z ) D Hk (z ) D: Hằng số k1 D x(n) y(n) H1(z) H2(z) HQ(z) 123 3.5.Khảo sát hệ bậc 1 a0 = b0 = 1, a1 = -a y(n) – a y(n-1) = x(n) • Hàm truyền đạt Y(z) az1 Y(z) X(z) Y (z) H(z) 1z X (z) 1 a z 1 za H(z) có 1 điểm không tại z = 0 và 1 điểm cực tại z = a • Ổn định: Hệ ổn định nếu |a| 1 • Nhân quả: h(n) = anu(n) nếu |z| > |a| • Phản nhân quả:h(n) = -anu(-n-1) nếu |z| < | a| • Hệ nhân quả và ổn định nếu |a| < 1 • Đáp ứng tần số H(ej ) = H(z)|z = ej 124 Ví dụ: Đáp ứng biên độ và pha 8 8 6 6 4 4 2 2 Magnitude (dB) Magnitude 0 Magnitude (dB) Magnitude 0 -2 -2 -4 -4 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Normalized Angular Frequency ( rads/sample) Normalized Angular Frequency ( rads/sample) 0 30 -5 25 -10 20 -15 15 -20 10 Phase (degrees) Phase (degrees) -25 5 -30 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Normalized Angular Frequency ( rads/sample) Normalized Angular Frequency ( rads/sample) a=0,5 a=-0,5 125 3.6.Khảo sát hệ bậc 2 a0 = b0 = 1 y(n) + a1 y(n-1)+a2y(n-2) = x(n) • Hàm truyền đạt Y(z) az12 Y(z) az Y(z) X(z) 1 2 Y (z) 2 H(z) 1z X (z) 1 a z1 a z 2 z 2 a z a 1122 • 1 điểm không bậc 2 tại z = 0 • 2 điểm cực a a2 4 a p 11 2 1,2 2 126 • Ổn định và nhân quả: |p1| < 1, |p2| < 1 a a22 4a 2 a a 4a 2 1 122 1 1 a2 Ranh giới điểm cực thực và phức: a 1 2 4 Xét điểm cực thực: 2 a a2 4a 2 (*) 11 2 2 a a2 4a 2 (**) 11 2 a a2 4a 2 a> -(1+a) (*) 1 122 1 a a2 4a 2 a> a-1 1 122 1 (**) cho kết quả tương tự 127 Xét điểm cực phức: a j 4 a a2 p 112 1 2 a j 4 a a2 p 112 2 2 p p a a < 1 1 22 2 128 a2 a2 a 1 2 4 1 a2=1 -2 -1 1 2 a1 -1 a2 = -1+a1 a2 = -(1+a1) Hệ ổn định và nhân quả nếu a1 và a2 thuộc miến tam giác. 129 Ví dụ: Đáp ứng biên độ và pha 10 10 5 5 0 0 Magnitude (dB) Magnitude Magnitude (dB) Magnitude -5 -5 -10 -10 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Normalized Angular Frequency ( rads/sample) Normalized Angular Frequency ( rads/sample) 70 0 60 -10 50 -20 40 -30 30 -40 Phase (degrees) Phase (degrees) 20 -50 10 -60 0 -70 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Normalized Angular Frequency ( rads/sample) Normalized Angular Frequency ( rads/sample) 1) 2) 1) a1 = 1, a2 = 0,5 2) a1 = -1, a2 = 0,5 130 Ví dụ:Xử lý ảnh. Ảnh qua bộ lọc thông thấp (làm trung bình) 131 Ví dụ: Ảnh qua bộ lọc thông cao (đạo hàm) 132 Bài tập chương 3 (1/2) 1. Hệ TT-BB có quan hệ vào ra: 1 y(n) x(n 1) x(n) x(n 1) 3 a) Xác định đáp ứng tần số b) Xác định và vẽ dạng đáp ứng biên độ. Nhận xét tính chất lọc của hệ. 2. Hàm truyền đạt của bộ lọc số có dạng: H(z) = 1 + 2z-1 + 4z-3 a) Xác định PT-SP biểu diễn quan hệ vào-ra b) Vẽ sơ đồ khối thực hiện bộ lọc 133 H(ej ) F F-1 h(n) z=ej Z Z-1 H(z) 134 Bài tập chương 3 (2/2) 3. Hệ TT-BB có hàm truyền đạt: H(z)=(1+az-1)/(1+bz-1+cz-2) với a,b,c là hằng số. a) Xác định quan hệ vào-ra của hệ b) Vẽ sơ đồ dạng chuẩn tắc thực hiện hệ. 135 Giải bài tập chương 3 (1) 1. 1 a) Đáp ứng xung: h(n) (n 1) (n) (n 1) 3 Đáp ứng tần số: j j n11 j j H(e) h(n)e e 1e (12cos) n 33 b) Đáp ứng biên độ: |H(ej )|=(1/3)|1+2cos | |H( )| 1.2 1 0.8 0.6 0.4 0.2 0 2 /3 136 Giải bài tập chương 3 (2) 2. a) H(z) = 1 + 2z-1 + 4z-3 = Y(z)/X(z) Y(z) = X(z) + 2z-1X(z) + 4z-3 X(z) y(n) = x(n) + 2x(n-1) + 4x(n-3) b) x(n) y(n) z-1 2 z-1 z-1 4 137 Chương 4 PHÉP BIẾN ĐỔI FOURIER RỜI RẠC 138 4.1. Chuỗi Fourier rời rạc của tín hiệu rời rạc tuần hoàn (DFS: Discrete Fourier Serie) Xét tín hiệu xp(n) tuần hoàn với chu kỳ N: xp(n) = xp(n+kN), k nguyên Tín hiệu này không biểu diễn được bằng biến đổi z nhưng có thể biểu diễn bằng chuỗi Fourier thông qua hàm e mũ phức với các tần số là bội của tần số cơ bản 2 /N. j( 2 / N )n k ek (n ) e Đây là tín hiệu tuần hoàn theo k với chu kỳ N. k = 0,1,2,,N-1 139 4.1. Chuỗi Fourier rời rạc của tín hiệu rời rạc tuần hoàn Chuỗi Fourier biểu diễn tín hiệu rời rạc tuần hoàn: N1 2 1 j n k N xpp (n ) X (k )e (1) N k0 Xác định các hệ số Xp(k) theo xp(n) dựa vào tính chất trực chuẩn: N1 2 1 j n r 1 r = m N e N m: số nguyên N n0 0 r m N 2 j n r e N Nhân 2 vế xp(n) với và lấy tổng từ n=0 đến N-1 N 122 N 1 N 1 j n r1 j ( k r )n NN xpp (n )e X (k )e n 0N n 0 k 0 140 4.1. Chuỗi Fourier rời rạc của tín hiệu rời rạc tuần hoàn N 122 N 1 N 1 j n r1 j ( k r )n NN Thay đổi thứ tự lấy tổng xpp (n )e X (k ) e n 0 k 0N n 0 k – r = mN [] = 1, k – r mN [] = 0 k=r+mN và k < N m=0 và k = r N1 2 j n r N Sử dụng tính chất trực chuẩn ta có: xpp (n )e X (r ) n0 N1 2 j n k Hoặc là: N Xpp (k ) x (n )e (2) n0 Nhận xét • Xp(k) tuần hoàn theo k với chu kỳ N • Các công thức (1), (2) là biểu diễn chuỗi Fourier của tín hiệu rời rạc tuần hoàn. (1): Tổng hợp. (2): Phân tích 141 4.1. Chuỗi Fourier rời rạc của tín hiệu rời rạc tuần hoàn • Quan hệ với biến đổi z xp (n) 0 n N-1 Xét 1 chu kỳ của xp(n): x (n ) 0 n cßn l¹ i N1 nn X(z) x(n)z x(n)z n n 0 N1 2 j n k N 2 jk Mặt khác Xpp (k ) x (n )e vậy X (k ) X ( z ) p zeN n0 Im(z) 2 /N Re(z) 142 Ví dụ: Hãy tính các hệ số chuỗi Fourier của dãy tín hiệu tuần hoàn sau xp(n ) 1 -10 0 1 2 3 4 5 6 7 8 9 10 n 4 2 4 k j n k j s in ( k / 2 ) 1 0 1 0 Xp (k ) e e n0 s in ( k / 1 0 ) |Xp(k)| -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 k 143 4.2. Biến đổi Fourier rời rạc của tín hiệu có độ dài hữu hạn (DFT: Discrete Fourier Transform) Ta đã xét cách biểu diễn một tín hiệu rời rạc tuần hoàn bằng chuỗi Fourier. Bằng cách diễn giải thích hợp ta cũng có thể dùng cách biểu diễn như vậy cho các tín hiệu có độ dài hữu hạn. Có thể coi tín hiệu có độ dài hữu hạn N là tín hiệu tuần hoàn có chu kỳ N trong đó một chu kỳ chính là tín hiệu có độ dài hữu hạn xp (n ) 0 n N 1 xp (n ) x (n r N ) x (n ) r 0 n cßn l¹ i 144 4.2. Biến đổi Fourier rời rạc của tín hiệu có độ dài hữu hạn • Cặp công thức DFT N1 2 j n k x(n)eN 0 k N 1 X (k ) Biến đổi thuận (phân tích) n0 0 k cßn l¹ i N1 2 1 j n k X(k)eN 0 n N 1 x (n ) Biến đổi ngược (tổng hợp) N k0 0 n cßn l¹ i 145 4.3. Biến đổi nhanh Fourier (FFT: Fast Fourier Transform) • Tính trực tiếp DFT cần N2 phép nhân số phức và N(N-1) phép cộng số phức • Thuật giải FFT: phân tích DFT của dãy N số lần lượt thành DFT của các dãy nhỏ hơn • Điều kiện áp dụng thuật giải: N = 2m. • Số lượng phép toán giảm xuống còn Nlog2N 146 4.4. Các hàm cửa sổ x(n) n N • Lấy ra đoạn tín hiệu có độ dài N để phân tích • Tương đương nhân tín hiệu với hàm w(n) w(n) = 1 trong đoạn tín hiệu được lấy w(n) = 0 trong đoạn tín hiệu không được lấy x’(n) = x(n).w(n) • Mặc nhiên đã dùng cửa sổ chữ nhật ! 147 4.4. Các hàm cửa sổ X’(f) = X(f)*W(f) • Tín hiệu được phân tích có độ dài hữu hạn đã gây ra X’(f) X(f) có sai số khi tính biến đổi Fourier • Để giảm sai số có thể tăng N • Phương pháp hay dùng là chọn W(f) hay chọn w(n) • Cửa sổ chữ nhật gây sai số lớn nên thường dùng các cửa sổ khác như Hamming, Hanning, Kaiser, Blackman 148 4.4. Các hàm cửa sổ • Hàm cửa sổ Hamming, Hanning: 0.9 0.8 0.7 0.6 0.5 0.4 Hamming 0.3 0.2 0.1 Hanning 0 50 100 150 200 250 n 149 N=256 1. Giả thiết tín hiệu x(n) là tổng của 2 tín hiệu x1(n) và x2(n). x1(n) là tín hiệu cosin có tần số góc là 0,1rad/s, x2(n) cũng là tín hiệu cosin có tần số góc là 0,4rad/s. Người ta dùng bộ lọc thông cao FIR có độ dài đáp ứng xung bằng 3 với giả thiết h(0) = h(2) = và h(1) = để triệt tiêu tín hiệu x1(n) và cho qua hoàn toàn tín hiệu x2(n). Hãy xác định các hệ số , và vẽ sơ đồ khối thực hiện bộ lọc FIR này. 2. Hàm truyền đạt của hệ TTBB nhân quả có dạng như sau: a z 1 H ( z ) za với a là số thực. a. Xác định giá trị của a sao cho H(z) ứng với một hệ ổn định b. Lấy 1 giá trị đặc biệt của a trong số các giá trị này, biểu diễn các điểm cực, điểm không và miền hội tụ. c. Đánh giá |H(f)| 150 Bài tập lớn (1/2) Bộ lọc số FIR có PT-SP 1. y(n)=x(n) + 2x(n-1)-3x(n-3)+5x(n-4) Hãy lập trình bằng Pascal để xác định đáp ứng xung của bộ lọc này. -Khởi tạo tín hiệu trễ = 0 (xnt1, xnt2, xnt3, xnt4) -Gán xn = 1 (xung đơn vị) BĐ vòng lặp: - Tính tín hiệu ra yn (=hn) theo PT-SP - Trễ tín hiệu vào xn: xnt4 := xnt3; xnt3 := xnt2; xnt2 := xnt1; xnt1 := xn; ( sau buớc lặp đầu tiên phải gán xn := 0) 151 KT vòng lặp Bài tập lớn (2/2 ) 2. Bộ lọc số IIR có các hệ số như sau: a0 1.0000 b0 0.0252 a1 -9.7023 b1 -0.0615 a2 8.8979 b2 0.0684 a3 -12.7653 b3 -0.0800 a4 13.1148 b4 0.0976 a5 -4.0608 b5 -0.0800 a6 5.1226 b6 0.0684 a7 -1.7620 b7 -0.0615 a8 0.3314 b8 0.0252 Hãy lập trình bằng Pascal để xác định 100 mẫu đầu tiên của đáp ứng xung của bộ lọc này. 152 • Cho tín hiệu vào = xung đơn vị, tính tín hiệu ra theo PT-SP BEGIN - Khởi tạo các tín hiệu trễ = 0 (xnt1,,xnt8,ynt1,,ynt8) - Gán xung đơn vị xn = 1 BĐ vòng lặp M - Tinh wn theo công thức (1)w(n) b x(n k) (1) k k0 - Tính y[n] theo công thức (2) N y(n) w(n) ay(nk k) (2) k1 - Trễ tín hiệu xn và yn (* Sau bước lặp đầu tiên phải gán xn = 0) KT vòng lặp END 153 Kết quả có dạng 0.25 0.2 0.15 0.1 0.05 0 -0.05 -0.1 -0.15 -0.2 -0.25 0 10 20 30 40 50 60 70 80 90 100 154 BÀI TẬP 1) Hệ TT-BB có tín hiệu vào x(n) = u(n) – u(n-2), h(n) = u(n) – u(n-2). Hãy xác định và vẽ tín hiệu ra y(n). 2) Cho hệ TT-BB có quan hệ vào ra: y(n) = x(n) + 3x(n-1) – 2x(n-3) + 5x(n-4) a) Xác định đáp ứng xung của hệ b) Hệ có ổn định không ? Tại sao ? c) Vẽ sơ đồ khối thực hiện hệ. 3) Cho hệ TT-BB có PT-SP: y(n) = x(n) –x(n -1) – 0,5 y(n -1) a) Xác định hàm truyền đạt b) Vẽ điểm cực điểm không của hệ, xét tính ổn định và nhân quả c) Xác định đáp ứng xung để hệ nhân quả. 155
File đính kèm:
 bai_giang_xu_ly_tin_hieu_so_ban_hay.pdf
bai_giang_xu_ly_tin_hieu_so_ban_hay.pdf

