Bài giảng Trường điện từ - Chương 3: Trường từ tĩnh

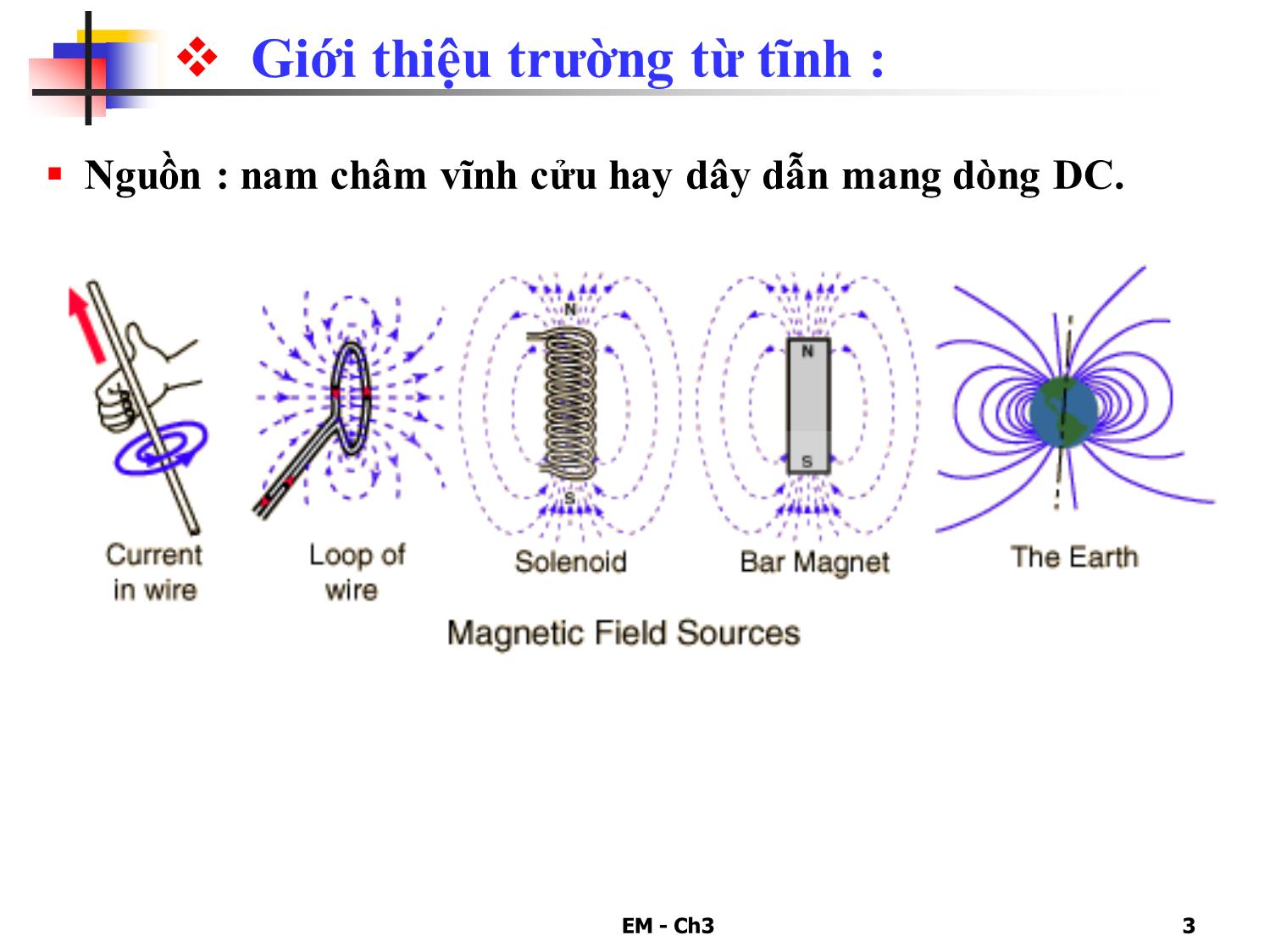
và thông dụng 
EM - Ch3 16 
a) Các phân bố dòng đối xứng: 
Đường Ampere là hình tròn 
i. Dây dẫn mang dòng dài vô hạn: 
zJ J.a
Đường Ampere là hình chữ nhật 
ii. Mặt mang dòng rộng vô hạn: 
S S yJ J .a
Dùng luật Biot-Savart: 
H H.aBiot-Savart & H const trên đường tròn 
H Mặt mang dòng và H = const bên ngoài mặt 
EM - Ch3 17 
b) Áp dụng luật Ampere: 
H & B.1. Xác định tính đối xứng của bài toán và dạng: 
4. Viết lại dạng vectơ đặc trưng cho trường từ. 
3. Dùng luật Amper, suy ra biên độ vectơ trường từ. 
*I
H
L
* *
C
H I H.L Id l
2. Chọn đường Amper thích hợp : H ( or ) d l
Và phải đi qua điểm cần tính trường từ. 
EM - Ch3 18 
 Lưu ý: 
 Với lõi trụ mang dòng, đường Amper là đường tròn, cường độ 
trường từ xác định theo : *I
H
2 r
Chỉ cần tìm I* . 
 Lõi bán kính R mang dòng I phân bố 
đều: mật độ dòng trong lõi: J = I/( R2). 
Và phần dòng bên trong đường Amper 
xác định: * 2I J.( r )
 Khi lõi mang dòng có mật độ dòng J là hàm 
theo tọa độ : J = J(r), phần dòng bên trong 
đường Amper xác định theo : 
2
*
0 0
I J(r)[ ]
r
rdrd
EM - Ch3 19 
VD 3.2.1: PP dùng luật Ampere 
*I I
H
2 r 2 r
 Áp dụng luật Amper : 
Tìm trường từ bên ngoài dây dẫn mang dòng I ? 
Giaûi 
 Ta thấy bài toán đối xứng trụ: H H.a
 Chọn đường Amper là đường tròn, 
 bán kính r , tâm tại dây dẫn. 
I
H a
2 r
 Vectơ cường độ trường từ: 
EM - Ch3 20 
VD 3.2.1: Thí nghiệm kiểm chứng 
a) Trước khi có dòng điện: b) Sau khi có dòng điện: 
 Đặt các kim la bàn trên mặt phẳng vuông góc dây dẫn. 
EM - Ch3 21 
VD 3.2.1: Minh họa bằng số 
Dây dẫn mang dòng I = 50A. 
2m 
P Bp 
 Tại P (cách trục dây dẫn 2m) . 
 Vectơ cảm ứng từ tiếp xúc đường tròn. 
 Và độ lớn: 
7
0
P
I 4 .10 50
B 5 (μT)
2 r 2 .2
EM - Ch3 22 
VD 3.2.2: PP dùng luật Ampere 
1. Xét miền r < R (trong lõi) : 
Cho lõi trụ đặc, bkính R, mang dòng I , tìm cảm ứng từ bên 
trong và bên ngoài lõi biết = 0 ? 
Giải 
2
* 0 2
0 1 0
1 2
I
r
I I.rRB
2 r 2 r 2 R
 Áp dụng luật Amper: 
 Đường Amper là đường tròn, bkính r , và: B.2 r = I* . 
 Ta thấy bài toán đối xứng trụ: B B.a
 Đường Amper: 
EM - Ch3 23 
VD 3.2.2: PP dùng luật Ampere (tt) 
*
0 2 0
2
I I
B
2 r 2 r
 Áp dụng luật Amper: 
2. Xét miền r > R (ngoài lõi) : 
 Đường Amper : 
 Vậy: 
0
2
0
Ir
 for r R
2 R
B
I
 for r R
2 r
EM - Ch3 24 
VD 3.2.2: Minh họa bằng số 
Lõi mang dòng I = 100A , bán kính R = 0,5cm. 
 Mật độ dòng trong lõi: 
6
2
-6
100 4.10
J (A/m )
.25.10
a) Cảm ứng từ trong lõi: 
2 7 6
0
1
(J. r ) 4 .10 4.10
B 0,8 ( )
2 r 2
r r T
b) Cảm ứng từ ngoài lõi : 
7 5
0
2
(I) 4 .10 100 2.10
B ( )
2 r 2
T
r r
EM - Ch3 25 
VD 3.2.3: PP dùng luật Ampere 
s x0J J a [A/m]
Tìm trường từ bên ngoài mặt mang 
dòng với mật độ mặt: 
Giaûi 
 Bằng xếp chồng ta CM được bên ngoài mặt mang dòng: 
H=const
H // mp(xOy)
EM - Ch3 26 
VD 3.2.3: PP dùng luật Ampere (tt) 
1
H J
2
o
*
o
abcda
H I H. H J .d l l l l
 Đường Amper là hình 
 chữ nhật abcd : 
EM - Ch3 27 
VD 3.2.3: PP dùng luật Ampere (tt) 
na Vectơ pháp tuyến, hướng vào miền chứa điểm khảo sát . 
 Tổng quát dưới dạng vectơ: 
s n
1
H J a
2
s x0J J a [A/m]
Tìm trường từ bên ngoài mặt mang 
dòng với mật độ mặt : 
Giải 
EM - Ch3 28 
VD 3.2.3: Minh họa bằng số 
Giaûi 
Dây dẫn phẳng, rộng w = 3m, mang 
dòng I = 60A. Tìm trường từ bên ngoài 
mặt mang dòng ? 
s x
I
J a 20 [A/m]
w
xa
 Mật độ dòng mặt: 
na za Miền z > 0 : 1 x yH 10 10a (A/m)za a
na za Miền z < 0 : 2 x yH 10 10a (A/m)za a
1H
2H
EM - Ch3 29 
3.3 Thế từ vector: 
EM - Ch3 30 
a) Thế từ vô hướng m : 
J
1rotH J
2rotH 0
 Ở miền không có dòng: rotH 0
 Ở miền có dòng: rotH J
Trường từ có tính xoáy, giải dùng thế vectơ có tính tổng 
quát hơn . 
Trường từ có tính thế: mH grad
( m : thế từ vô hướng [A]) 
EM - Ch3 31 
b) Thế từ vector A : 
div B 0 (IV)
div(rot A) 0 (gtvt)
 Định nghĩa: 
 Thế vectơ có tính đa trị, dùng điều 
kiện phụ để đơn giản hóa phương trình: 
B rot A
divA 0
 Đơn vị của thế vectơ : [Wb/m] hay [T.m] 
EM - Ch3 32 
c) Phương trình Poisson của thế từ vector: 
 Giả sử môi trường đẳng hướng, TT, đnhất: = const : 
J rot H (1)Có: 
J rot B rot(rot A) grad(divA) A
A J
( phương trình Poisson 
của trường từ tĩnh ) 
EM - Ch3 33 
d) Nghiệm Pt Poisson của trường từ tĩnh : 
 Đ/v dòng khối: 
V
J
A .
4 r
dV
 N.xét 1: Nguồn gốc trường từ 
 là yếu tố dòng. 
L
I
A
4 r
d l
 N.xét 2: Thế vectơ cùng phương , 
chiều với yếu tố dòng dây . 
J 
dl 
dA 
P 
r 
I 
L 
J JS IdV d l d l
 Đ/v dòng dây: 
EM - Ch3 34 
e) Điều kiện biên của thế vector A : 
e1) Điều kiện liên tục: 
1 2A ( ) A ( )S S
Do là nghiệm ptrình Poisson, thế vectơ phải thỏa điều kiện 
liên tục. Trên biên S của hai môi trường ta có: 
e2) Điều kiện biên của trường từ: 
B rotADo định nghĩa từ : 
Nên thành phần pháp tuyến và tiếp tuyên của rotA cũng 
phải thỏa các điều kiện biên của trường từ. 
EM - Ch3 35 
f) Từ thông tính theo thế vector A : 
m
C
A d l
m
S S
B S rot A Sd dCó: 
 Dựa vào định lý Stokes : 
EM - Ch3 36 
g) Xác định thế vector A 
i. Giải trực tiếp thế vectơ từ phương trình Poisson. Dùng ĐKB 
xác định các hằng số tích phân. 
A J
(phương trình Poisson 
của trường từ tĩnh ) 
EM - Ch3 37 
ii. Sự tương tự giữa A và : 
Trường từ tĩnh (có Js = 0) Trường điện tĩnh (có s = 0) 
A J ; B rot A V
ρ
; E grad( )
V, E, ρ , ρ , , ...1A, B, I, J, , ...
C
H Id l
0S
D S ρd
A B. r Cd E. r Cd
Và có sự tương tự giữa: 
 Nếu: 
zJ J(x,y)a Thì : z zA A(x,y)a A.a
EM - Ch3 38 
 Qui trình xác định A tương tự : 
Trục điện Trục dòng 
E B
Edr C, ... A Bdr C, ...
Mặt Gauss Đường Amper 
Trường điện tĩnh Trường từ tĩnh 
EM - Ch3 39 
 VD 3.3.1: Tính thế vector A 
 Đường Ampere là đường tròn, bán kính r. Theo phương pháp 
đường Ampere, ta có: 
 Bài toán đối xứng trụ. 
Chọn hệ tọa độ trụ. 
0μ IB
2 r
r 
z 
B 
a) Xác định cảm ứng từ : 
0μ IB a
2 r
Dây dẫn dài vô hạn mang dòng I, trong môi trường không khí. 
Xác định: (a) Vector cảm ứng từ bên ngoài dây dẫn ? (b) Thế 
vector bên ngoài dây dẫn ? (c) Tình từ thông gởi qua khung dây 
hình chữ nhật đặt song song dây dẫn ? 
Giải 
EM - Ch3 40 
 VD 3.3.1: Tính thế vector A (tt) 
b) Xác định thế vector : theo sự tương tự giữa trường từ và điện: 
a 
z 
b 
L 
A 
B 
C 
D 
c) Xác định từ thông gởi qua khung dây ABCD: 
m r=a r=bA A .L 0 A .L 0
ABCD
d
0μ I C
r a 2π a
A ln
0μ I C
r b 2π b
; A ln
0μ I b
m 2π a
ln
0 0μ I μ I C
2πr 2π r
A B dr C' ' lndr C zA Aa
EM - Ch3 41 
 Các công thức xác định A tương tự : 
I C
A ln
2 r
a. Trục mang điện : a. Trục mang dòng I : 
ρ C
ln
2 r
b. Hai trục mang điện : b. Hai trục mang dòng I : 
-
+
I r
A ln
2 r
-
+
ρ r
ln
2 r
EM - Ch3 42 
3.4 Năng lượng trường từ (Wm) 
EM - Ch3 43 
a) Tính theo các đại lượng đặc trưng : 
2 2 3
m
1 1 1
w HB H B (J/m )
2 2 2
= Mật độ NL trường từ 
2
2
m
V V V
1 1 1 B
W B.H H
2 2 2
dV dV dV
(V : khoâng gian toàn taïi tröôøng töø) 
EM - Ch3 44 
b) Tính theo A và J : 
H.rot A div(A H) A. H div(A H) A. Jrot Có: 
m
V V
1 1
W B.H. H.(rot A)
2 2
dV dV Từ : 
m
V S
1 1
W A. J A H. S
2 2
dV d
r
S S
A H. S lim( A H. S) 0d d
JV V
A. J A. JdV dV
 Mà: 
J
m
V
1
W A. J
2
dV
(VJ: miền có dòng) 
EM - Ch3 45 
c) NL trường từ của hệ N dòng dây: 
J k k
n n
m k
k 1 k 1V V C
1 1 1
W A. J . A. J A I
2 2 2
dV dV d l
 Cho hệ n dòng điện dây: I1  In ; 1  n : 
n
m k k
k 1
1
W I
2
 Vậy : 
k
n n
m k k k
k 1 k 1C
1 1
W I A I
2 2
d l
EM - Ch3 46 
 Các trường hợp đặc biệt: 
2
m
1 1
W I LI
2 2
 Ta có: 
i. n = 1 : Một vòng dây mang dòng 
ii. n = 2 : Hai vòng dây mang dòng 
m 1 1 2 2 1 1 1 2 2 1 2 2
1 1 1 1
W I I I (L I MI ) I (MI L I )
2 2 2 2
 Ta có: 
2 2
m 1 1 2 2 1 2
1 1
W L I L I MI I
2 2
 Đây là công thức xác định NLTT trong phần tử hỗ cảm. 
EM - Ch3 47 
 VD 3.4.1: Tính năng lượng trường từ 
Cuộn dây hình xuyến (toroid) N vòng, tiết 
diện hình chữ nhật, bán kính trong là a, 
ngoài là b,cao là h (hình a). Xác định: (a) 
cường độ trường từ trong lõi khi có dòng I 
chạy qua toroid ? (b) Năng lượng trường từ 
tích lũy trong lõi có = const ? 
Giải 
 Đường Ampere là đường tròn, bán kính r. 
 Bài toán đối xứng trụ. Chọn hệ tọa độ trụ. 
NI
H
2 r
 Tổng dòng bên trong : NI (hình b). Ta có: 
EM - Ch3 48 
 VD 3.4.1: Tính năng lượng trường từ (tt) 
Cuộn dây hình xuyến (toroid) N vòng, tiết 
diện hình chữ nhật, bán kính trong là a, 
ngoài là b,cao là h (hình a). Xác định: (a) 
cường độ trường từ trong lõi khi có dòng I 
chạy qua toroid ? (b) Năng lượng trường từ 
tích lũy trong lõi có = const ? 
Giải 
2 2
2 2
2
1 μ N I2
m 2 2 4π r0 0
W μH dV ( )
b h
V a
rdrd dz
 Năng lượng trường từ: 
2 2μN I b
m 4π a
W ln h
EM - Ch3 49 
3.5 Tính toán điện cảm: 
EM - Ch3 50 
a) Điện cảm bản thân và hỗ cảm: 
 Định nghĩa điện cảm (self inductance) : 
1 11 1L I ( )H
 Gọi 11 : từ thông gởi qua vòng dây 1 
do dòng I1 tạo ra . 
 Gọi 21 : từ thông gởi qua vòng dây 2 
do dòng I1 tạo ra . 
 Xét 2 vòng dây, dòng I1 chạy qua vòng 
dây 1 . 
21 1M I ( )H Đnghĩa hỗ cảm (mutual inductance) : 
EM - Ch3 51 
b) Thuật toán chung tính L hay M : 
i. Chọn hệ tọa độ. 
ii. Giả sử dòng điện I chạy qua hệ . 
v. Nếu là cuộn dây N vòng thì từ thông móc vòng m = N. m . 
vi. Xác định L = m/I . 
iv. Tìm từ thông móc vòng m : 
m
C
BdS A
S
d
iii. Tìm B (hay A ) do dòng I tạo ra . 
EM - Ch3 52 
c) P2 dùng năng lượng trường từ : 
2 2 2
V V
1 1
W LI B H
m 2 2 2
dV dV m
2
2W
L
I
m mtr mngW W W
Wmtr: năng lượng TT trong miền có dòng. 
Wmng: năng lượng TT ngoài miền có dòng. 
mtr
tr 2
2W
L
I
1. Điện cảm trong : 
mng
ng 2
2W
L
I
2. Điện cảm ngoài: 
EM - Ch3 53 
 Tính Ltr theo từ thông móc vòng: 
mtr
tr
total
L
I
mtr
total
I
BdS
IS
Từ thông móc vòng qua phần tiết diện mang dòng S do chỉ 
phần dòng điện trong miền có dòng tạo ra: 
EM - Ch3 54 
d) Các ví dụ tính điện cảm & hỗ cảm: 
VD3.5.1: Tính điện cảm riêng L0 của solenoid 
không khí, dài L, tiết diện A (hình tròn bkính 
R) , gồm N vòng dây ? 
Giaûi 
 Mặt cắt dọc solenoid: 2 mặt mang dòng. 
 Trường từ chỉ tồn tại bên 
trong solenoid : 
0 0 S 0
NI
B μ H μ J μ
L
EM - Ch3 55 
VD 3.5.1: Tính điện cảm của solenoid (tt) 
 Từ thông gởi qua N vòng của solenoid : 
 Điện cảm của solenoid : 
0L
I
2
0 0
N A
L
L
N N.B.A 2; (A πR )
EM - Ch3 56 
VD 3.5.2: Tính điện cảm của toroid. 
Tính điện cảm riêng L0 của toroid ? 
Giaûi 
 Trường từ chỉ tồn tại trong 
toroid , và : 
B.2πr μNI
 Mặt cắt ngang toroid: 
 Đường Amper: 
EM - Ch3 57 
VD 3.5.2: Tính điện cảm của toroid (tt) 
 Từ thông gởi qua N vòng dây toroid : 
2
0
N h b
L ln
2 a
b h2
S
a 0
N I .
N N B
2
dr dz
dS
r
2N I b
N ln .h
2 a
EM - Ch3 58 
VD 3.5.3: Tính điện cảm của đường dây 
Điện cảm đơn vị L0 của đường dây 
song hành ? 
Giải 
0 0L I Đnghĩa: 
0
MNPQ
A A Ad l Có: 
I d-a
2 a
I a
2 d-a
A ln
A ln
,với: 
0
I d a
ln
a
0
d a
L ln
a
EM - Ch3 59 
VD 3.5.4: Tính điện cảm của cáp 
0
MNPQ
Ad l
0 0L I Dùng: 
1 20 r r r r
A A
1 1
2 2
I C
r r 2 r
I C
r r 2 r
A ln
A ln
 Mà: 
2
0
1
I r
ln
2 r
2
0
1
r
L ln
2 r
Điện cảm đơn vị L0 của 
cáp đồng trục ? 
Giaûi 
EM - Ch3 60 
VD 3.5.5: Tính hỗ cảm hệ đường dây 
12
2
Φ
z 0 I
A A i M
1
212 2 2
C
; A A Ad l
2 12'
12
2 1'2'
1'2
I d
2 2 d
I d
2 2 d
A ln
A ln
2 12' 1'2
12 1'2'
I d d
12 2 d d
ln 12' 1'2
12 1'2'
d d
2 d d
M ln
Hỗ cảm đơn vị của 2 hệ trục mang dòng song song ? 
EM - Ch3 61 
VD 3.5.6: Tính điện cảm dùng MATLAB 
Dây dẫn bán kính a = 1 mm uốn thành vòng dây tròn bán kính 
10 cm. Bỏ qua điện cảm trong của dây dẫn, viết chương trình 
MATLAB tính điện cảm của vòng dây này. 
% Inductance inside a conductive loop 
% This modifies ML0302 to calculate inductance 
% of a conductive loop. It does this by 
% calculating the mag field at discrete, 
% points along a pie wedge then calculates flux 
% through each portion of the wedge. Then it 
% multiplies by the number of wedges in the 'pie'. 
% Variables: 
% I current(A) in +phi direction on ring 
% a ring radius (m) 
% b wire radius (m) 
% Ndeg number of increments for phi 
% f angle of phi in radians 
% df differential change in phi 
% dL differential length vector on the ring 
% dLmag magnitude of dL 
% dLuv unit vector in direction of dL 
% [xL,yL,0] location of source point 
% Ntest number of test points 
% Rsuv unit vector from O to source point 
% R vector from the source to test point 
% Ruv unit vector for R 
% Rmag magnitude of R 
% dH differential contribution to H 
% dHmag magnitude of dH 
% radius radial distance from origin 
% Hz total magnetic field at test point 
% Bz total mag flux density at test point 
% flux flux through each differential 
segment 
clc %clears the command window 
clear %clears variables 
EM - Ch3 62 
VD 3.5.6: Tính điện cảm dùng MATLAB 
% Initialize Variables 
a=0.1; 
b=1e-3; 
I=1; 
Ndeg=180; 
Ntest=60; 
uo=pi*4e-7; 
df=360/Ndeg; 
dLmag=(df*pi/180)*a; 
dr=(a-b)/Ntest; 
% Calculate flux thru each segment of pie 
wedge 
for j=1:Ntest 
 x=(j-0.5)*dr; 
 for i=(df/2):df:360 
 f=i*pi/180; 
 xL=a*cos(f); 
 yL=a*sin(f); 
 Rsuv=[xL yL 0]/a; 
 dLuv=cross([0 0 1],Rsuv); 
 dL=dLmag*dLuv; 
 R=[x-xL -yL 0]; 
 Rmag=magvector(R); 
 Ruv=R/Rmag; 
 dH=I*cross(dL,Ruv)/(4*pi*Rmag^2); 
 dHmag(i)=magvector(dH); 
 end 
 Hz(j)=sum(dHmag); 
 Bz(j)=uo*Hz(j); 
 dSz(j)=x*df*(pi/180)*dr; 
 flux(j)=Bz(j)*dSz(j); 
end 
fluxwedge=sum(flux); 
Inductance=Ndeg*fluxwedge 
Now run the program: 
Inductance = 5.5410e-007 
or 
L = 550 nH 
EM - Ch3 63 
 VD 3.5.7: Tính trường từ tĩnh 
2
2
a 2 2
r 0
0 a
0 0
J πa
I J (1 )[ ]
2
rdrd
a) Tổng dòng trên lõi: chọn hệ trụ. 
z 
a 
z 
I 
= 
Lõi trụ đặc, dài vô hạn, bán kính là a, mang dòng với mật độ: 
Giải 
Lõi có độ thẩm từ µ = const. Bên ngoài là không khí. Xác định: 
(a) Tổng dòng trên lõi ? (b) Cường độ trường từ trong lõi ? (c) 
Năng lượng trường từ tích lũy bên trong lõi trên đơn vị dài ? 
Suy ra điện cảm trong của lõi trên đơn vị dài ? 
2
2
r
0 za
J J (1 )a
EM - Ch3 64 
 VD 3.5.7: Tính trường từ tĩnh (tt) 
 Bài toán đối xứng trụ. Đường Ampere là đường tròn, 
bán kính r. Theo phương pháp đường Ampere, ta có 
tổng dòng bên trong : 
b) Xác định cường độ trường từ: 
3
2
*
r r
0 2 4a
I
H J
2 r
2 2 4
2 2
2
r r r*
0 0 2a 4a
0 0
I J (1 )[ ] J ( )2
r
rdrd
c) Xác định năng lượng trường từ trên 1m dài: 
z 
r 
H 
1m 
2 4 6
2 4
a 2 1
1 1 r r r2 2
mtr 02 2 4 4a 16a0 0 0
W μH μJ ( )
V
dV rdrd dz
EM - Ch3 65 
 VD 3.5.7: Tính trường từ tĩnh (tt) 
z 
r 
H 
1m 
4 6 8 4
2 4
π a a a π 83a2 2
mtr 0 02 4 2 38424a 128a
W μJ μJ
4
2 2 4
0
π 83a 42
02 38
mtr
2 J πr 4 at
2 μ
2W
JL
I
 Điện cảm trong: 
tr
83μ
L
96π