Bài giảng Trường điện từ - Chương 1: Vector và trường
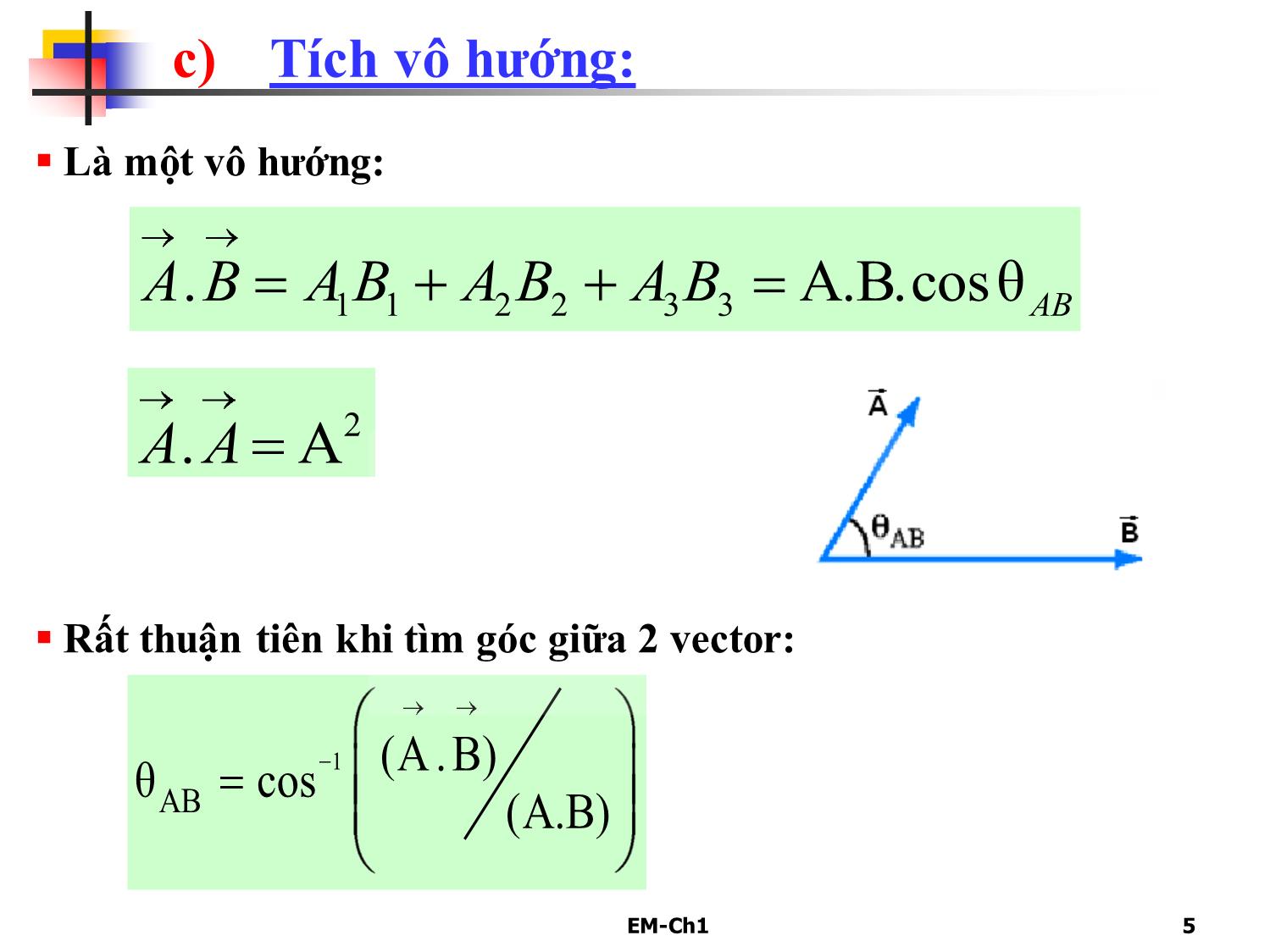
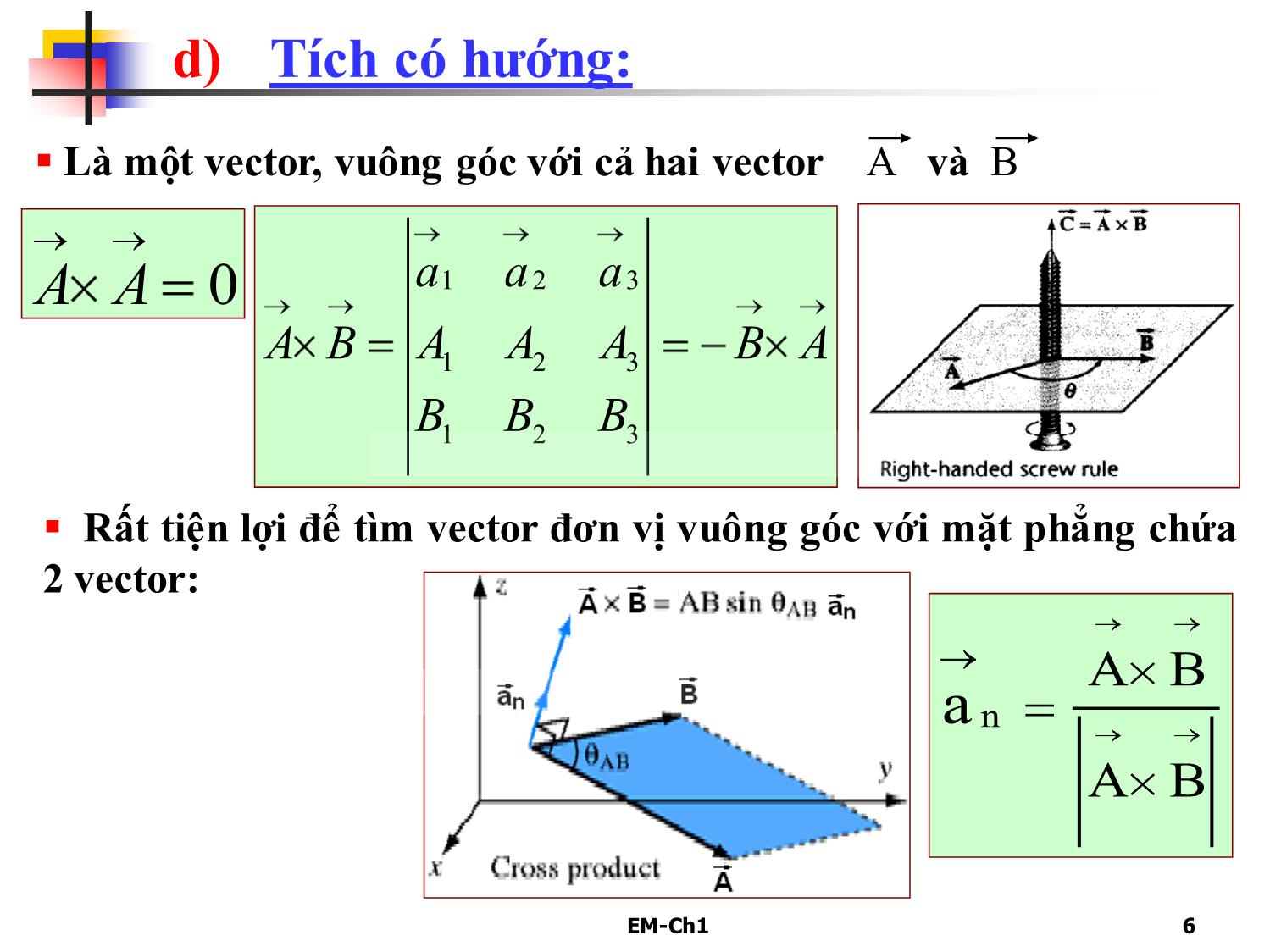
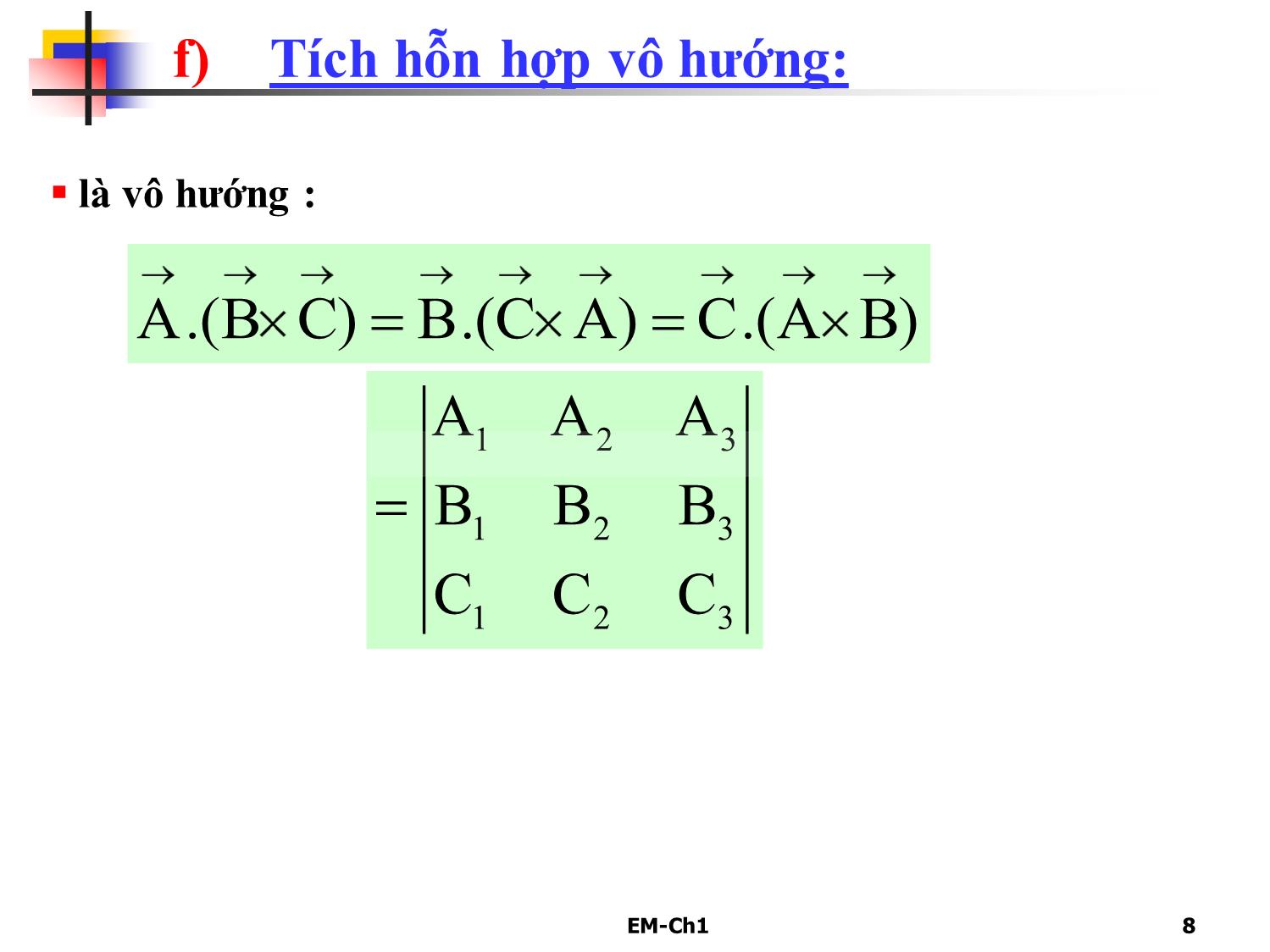
1.1 Đại số vector.
1.2 Các hệ tọa độ.
1.3 Yếu tố vi phân và các tích phân.
1.4 Các toán tử cơ bản.
1.5 Khái niệm trường điện từ.
1.6 Các định luật cơ bản của trường điện từ.
1.7 Dòng điện dịch - Hệ phương trình Maxwell.
1.8 Điều kiện biên của trường điện từ.

Trang 1

Trang 2

Trang 3

Trang 4
Trang 5
Trang 6

Trang 7
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Trường điện từ - Chương 1: Vector và trường", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Trường điện từ - Chương 1: Vector và trường

q
Với:
q > 0
B
Fm
Magnetic field line
v S N
Điện tích điểm nếu
chuyển động bên
cạnh một nam châm:
chịu tác dụng của
một lực.
Ta nói bên ngoài nam chaâm tồn tại một trường từ , đặc
trưng bởi:
Vector cảm ứng từ B :
EM-Ch1 83
Vector cường độ trường từ H :
Nếu từ môi đẳng hướng và tuyến tính: M Hm
0 0B (1 ) H Hm r
= 0 r = độ thẩm từ tuyệt đối của môi trường [H/m].
r = độ thẩm từ tương đối [0].
m = độ cảm từ [0].
1
0
H B M [ / ]A m
= hằng số từ.
7
0
4 .10 [ / ]H m
Môi trường chân không: 1
0
H B [ / ]A m
Môi trường từ môi:
(Vectơ phân cực từ)
B H
EM-Ch1 84
Độ thẩm từ tương đối của một số vật liệu:
EM-Ch1 85
Dòng điện:
Định nghĩa : I (A)
dq
dt
Là nguồn tạo ra trường từ. Có 2 mô hình cơ bản:
EM-Ch1 86
i. Vector mật độ dòng khối :
+ chiều trùng chiều dòng.
+ độ lớn: J = dI/dS
I J.dS
S
Dòng điện chạy qua diện tích S :
Đặc điểm của vectơ mật độ dòng
khối:
: Độ dẫn điện [ / ][1/ ]S m m
J E Định luật Ohm:
EM-Ch1 87
ii. Vector mật độ dòng mặt :
+ chiều trùng chiều dòng.
+ độ lớn: Js = dI/dℓ
s
L
I J dl Dòng điện chạy qua đường L :
Đặc điểm của vectơ mật độ dòng
mặt :
EM-Ch1 88
1.6
Các định luật cơ bản của
trường điện từ
EM-Ch1 89
1.6.1 Luật bảo toàn điện tích :
Dòng điện thoát ra bên ngoài mặt kín S bằng tốc độ giảm
của điện tích chứa bên trong mặt S.
( )
dq
i t
dt
a) Phát biểu và dạng tích phân:
J S
S
dq
i d
dt
EM-Ch1 90
b) Phương trình liên tục:
J , V
V V
div dV dV V
t
J S
S
dq dt i d
V
V
dq dt dV
t
J S div J
V
S
d dV
J Vdiv t
(Phương trình liên tục = Dạng vi
phân của luật bảo toàn điện tích)
EM-Ch1 91
1.6.2 Luật Gauss về điện:
DdS V
S V
q dV
Thông lượng của vector cảm ứng điện thoát ra bên ngoài mặt
kín S bằng tổng điện tích chứa trong miền V giới hạn bởi mặt S
đó.
a) Phát biểu và dạng tích phân:
EM-Ch1 92
b) Dạng vi phân:
divD D V
Dạng vi phân của luật
Gauss về điện.
DdS V
S V
q dVTừ:
EM-Ch1 93
Ví dụ 1.6.1: Áp dụng luật Gauss
Tìm thông lượng của vector cảm ứng điện thoát ra bên ngoài mặt
S giới hạn bởi: x = 1, y = 1 và z = 1, biết mật độ điện tích khối
bên trong : 2 2 2
0, , 3V x y z x y z
1 1 1
2 2 2
0
1 1 1
1 1 1
2 2 2
0
0 0 0
0
0
3
8 3
1 1 1
8 3
3 3 3
16
V
S V
x y z
x y z
d dv
x y z dx dy dz
x y z dx dy dz
D S
EM-Ch1 94
1.6.3 Định luật Gauss về từ:
BdS 0
S
Thông lượng của vector cảm từ điện thoát ra bên ngoài mặt kín
S luôn bằng 0.
a) Phát biểu và dạng tích phân:
EM-Ch1 95
b) Dạng vi phân :
divB D 0
Dạng vi phân của luật
Gauss về từ.
BdS 0
S
Từ:
EM-Ch1 96
1.6.4 Định luật Ampere :
a) Phát biểu và dạng tích phân :
Lưu số của vector cường độ trường từ H dọc theo đường kín
(C) bất kỳ bằng tổng dòng chạy qua mặt S giới hạn bởi đường kín
(C) đó.
(Dạng tích phân ) encH I
C
d l
Ienc = Ik = I1 + I2 - I3
(C) I1
I
3
I
2
EM-Ch1 97
b) Dạng vi phân :
(Dạng vi phân) rot H J
encI J.dS
S
Do : encHdl = I JdS
C
S
encHdl I
C
Từ:
H l H S
C S
d rot dTheo định lý Stokes:
EM-Ch1 98
1.6.5 Định luật Faraday:
emf Edl = BdS
C
S
d
dt
a) Phát biểu và dạng tích phân:
EM-Ch1 99
b) Dạng vi phân :
B
... E S S,
S S
rot d d S
t
(C)
dS
B(t)
S
Dạng vi phân B
rotE E
t
E B S
C S
d
d l d
dt
Từ:
EM-Ch1 100
Thí nghiệm Faraday:
EM-Ch1 101
Ứng dụng của luật Faraday:
Máy phát DC Máy phát AC
EM-Ch1 102
Ví dụ 1.6.2: D2.5 in Rao’s book
0B =B (sin .a cos .a )x yt t
z
1
1
x
y
C
Cho: , xác định emf ?
0BdS sin
S
B tTa có:
0 0Edl = ( sin ) cos
C
d
emf B t B t
dt
EM-Ch1 103
emf < 0
emf > 0
B0
0
–B0
emf
0
2 3
2 3
inc.
dec.
– B0
t
t
B0
Kiểm chứng luật Lenz:
EM-Ch1 104
Ví dụ 1.6.3: Áp dụng luật Faraday
Cuộn dây N vòng tròn bán kính a, nằm trong mặt phẳng xOy,
tâm tại O, nối với điện trở R, đặt trong trường từ B = Bo(2ay +
6az)sinωt, ω là tần số góc, như hình vẽ bên dưới. Tìm:
a) Từ thông móc vòng
qua một vòng dây ?
b) Sức điện động cảm
ứng emf biết N = 10 ,
B0 = 0.2T, a =10cm, ω
= 103 rad/s ?
c) Cực tính của emf tại t
= 0 ?
d) Dòng điện I trong
mạch biết R = 1 kΩ ?
EM-Ch1 105
Ví dụ 1.6.3: Giải
a) Từ thông móc vòng qua một vòng dây :
2
0 0
S
B 2 6 sin . 6 B sin ωtm
S
t dS a
y z z
B.dS a a a
Khi N=10, a = 0.1 m, ω=103 rad/s and B0 = 0.2 T: emf = -377cos10
3t V
2 2
0 0b) emf 6 Na B sinωt 6 Nωa B cosωt
md dN
dt dt
c) Tại t = 0, emf = -377cos103t = - 377 volts : điểm 2 có thế cao
hơn điểm 1.
d) Dòng I trong mạch là : 3 3
3
emf 377
cos10 0.38cos10 Amps
10
I t t
R
EM-Ch1 106
1.7 Dòng điện dịch -
Hệ phương trình Maxwell:
EM-Ch1 107
a) Dòng điện dịch:
Từ luật Ampere: rot H J
Luật Ampere chỉ đúng với dòng điện DC !!!
div(rot H) div J V
t
0V
t
Do div(rot H) 0 (vector analysis)
EM-Ch1 108
a) Dòng điện dịch : (tiếp theo)
Từ phương trình liên tục:
D
div(J) 0 div(J ) 0
t t
V
Vector mật độ dòng dẫn : 2
cJ J [A/m ]
total
D
J J
t
Vector mật độ dòng dịch: 2
d
D
J [A/m ]
t
EM-Ch1 109
Luật Ampere-Maxwell:
(Dạng tích phân)
D
H J S
tC
S
d l d
(Dạng vi phân)
D D
rot H J E
t t
EM-Ch1 110
Ví dụ 1.7.1: Dòng điện dịch
Môi trường chân không ( = 0, = 0, = 0) tồn tại trường từ:
0 yH H sin a (A/m)t z
(Với β = const). Xác định: (a) Vector mật độ dòng dịch ? (b)
Vector cường độ trường điện ?
Giải
x y z
d x y z
H sin( )
0
2
(A/m )0 x
a a a
D
J rot H
0 0
H cos( )a
t z
t
t z
a) Do = 0 nên:
2
(A/m )d 0 xJ H cos( )at z
EM-Ch1 111
Ví dụ 1.7.1: Dòng điện dịch
Môi trường chân không ( = 0, = 0, = 0) tồn tại trường từ:
0 yH H sin a (A/m)t z
(Với β = const). Xác định: (a) Vector mật độ dòng dịch ? (b)
Vector cường độ trường điện ?
Giải
0βH 2
(C/m )xω
D
D sin( )adt t z
t
b) Từ câu (a) ta có:
0
0
βH
(V/m)xωε
E sin( )at z
EM-Ch1 112
b) Hệ phương trình Maxwell:
Luật bảo toàn điện tích:
Dạng tích phân Dạng vi phân
Edl = BdS
C
S
d
dt
(2)
B
rotE
t
DdS
S
q (3) VdivD ρ
BdS 0
S
(4) divB 0
J S
S
dq
d
dt
(5) J Vdiv t
(1)
D
H J S
tC
S
d l d Drot H J
t
EM-Ch1 113
Ví dụ 1.7.2: Hệ phương trình Maxwell
9
x y z
x y z0
5cos(10 βz)
9
x
a a a
H
rot E
0 0
5βsin(10 βz)a
t
t
t
Giải
Môi trường chân không ( = 0, = 0, = 0) tồn tại trường điện:
Dùng hệ phương trình Maxwell xác định β và vector cường độ
trường từ ?
9
yE(z,t) 5cos(10 ).a (V/m)t z
Từ pt(2) của hệ pt Maxwell: 0
B H
rotE
t t
9
x9
0
5β
H cos(10 βz)a
μ .10
t
EM-Ch1 114
Ví dụ 1.7.2: Hệ phương trình Maxwell
Từ pt(1) của hệ pt Maxwell: 0
D E
rotH ε
t t
9
x
5
H cos(10 )a (A/m)
120
t z
9
0
x y z
x y z
5β 9
μ .10
a a a
rot H
cos(10 βz) 0 0t
2
9
y9
0
5β
sin(10 )a
μ .10
t z
2
9
0 9
0
5β
5.ε .10
μ .10
3
10
9 9
0 0 yε 5ε 10 sin(10 βz)a
E
t
t
Và:
EM-Ch1 115
1.8 Điều kiện biên của trường điện từ :
EM-Ch1 116
a) Khái niệm:
na : 2 1
Lưu ý là trong các bài toán điều kiện biên, vector đơn vị pháp
tuyến của biên luôn chọn theo qui tắc: hướng từ môi trường 2
sang môi trường 1.
ĐKB = là các phương trình toán, mô tả sự ràng buộc của các
đại lượng đặc trưng của trường điện từ trên biên của hai môi
trường .
Môi
trường 1
Môi
trường 2
( 1; 1; 1)
( 2; 2; 2)
an
EM-Ch1 117
b) ĐKB cho thành phần pháp tuyến:
s
1 2n s
1 2n
ρ
1 2n
a (D D ) ρ
a (B B ) 0
a (J J )
t
s
1n 2n s
1n 2n
ρ
1n 2n
D D ρ
B B 0
J J
t
( 1; 1; 1)
an
( 2; 2; 2)
D2
D1
D2n
D1n
s
1n 2n s n
1n 2n
ρ
1n 2n n
(D D ) ρ .a
(B B ) 0
(J J ) .a
t
EM-Ch1 118
c) ĐKB cho thành phần tiếp tuyến :
1 2n
1 2n
a (H H ) J
a (E E ) 0
S
1 2
1 2
H H J
E E 0
t t S
t t
( 1; 1; 1)
an
( 2; 2; 2)
E2
E1
E2t
E1t
1t 2t S n
1t 2t
(H H ) J a
(E E ) 0
EM-Ch1 119
d) Các trường hợp đặc biệt:
EM-Ch1 120
TH1: Cả 2 môi trường điện môi
nn
t
t
EEDD
D
D
EE
2211n2n1
2
1
2
1
t2t1
Trường điện
nn
t
t
HHBB
B
B
HH
2211n2n1
2
1
2
1
t2t1
Trường từ
0, 0s SJ
Nếu cả 2 môi trường là điện môi lý tưởng thì không tồn tại dòng
mặt cũng như điện tích bề mặt trên biên 2 môi trường.
EM-Ch1 121
TH 2: Một môi trường là dẫn lý tưởng
Môi trường 1 Môi trường 2
0E t1
n 1a sH J
n 1 Sa ρD
0B n1
0E t2
0B n2
0H t2
0D n2
1
2
na
1H t
Js
1t SH J
2 Dẫn lý tưởng
(
2
)
1 Điện môi (
1
= 0)
na
S
1n
1
ρ
E
1E n
1
2
+ + + + + + + + + +
S
EM-Ch1 122
TH3: Cả 2 là môi trường dẫn
1
2
na
( 1; 1)
( 2; 2)
1
2
+ + + + + + + + + + Sρ
1nJ
2nJ
1J
2J
2tJ
1tJ
1t 2t
1t 2t
1 2
1n 2n 1 1n 2 2n
J J
E E
J J E E
Điều kiện đối với trường tĩnh:
Và trên biên :
1 1n 2 2n SE E ρ
EM-Ch1 123
e) Qui trình bài toán điều kiện biên:
1 1n 1tE E E
Giả sử biết trường điện trên biên về phía môi trường 1 (E1), xác
định trường điện trên biên về phía môi trường 2 (E2).
1. Xác định vector đơn vị pháp tuyến an.
2. Xác định các thành phần pháp tuyến & tiếp tuyến của E1.
3. Áp dụng ĐKB tìm E2.
1n 1 n nE (E .a ).a 1t 1 1nE E E
2 2n 2tE E E
Áp dụng ĐKB thành phần pháp tuyến xác định E2n.
Áp dụng ĐKB thành phần tiếp tuyến xác định E2t.
EM-Ch1 124
Ví dụ 1.8.1: Bài toán ĐKB
Mặt phẳng z = 0 là biên của hai môi trường: môi trường 2 chiếm
miền z 0 là
điện môi lý tưởng có 1r = 40. Biết trường điện trên biên về phía
môi trường chân không là :
Tìm trường điện trên biên về phía môi trường điện môi ?
2 x y zE 13a 40a 50a (V/m)
Giải
Xác định an:
Do vector đơn vị pháp tuyến
của biên hướng từ môi trường 2
sang môi trường 1 nên ta có :
n z a a
Môi trường 1
Môi trường 2
z = 0
biên
n a
z
EM-Ch1 125
Ví dụ 1.8.1: Bài toán ĐKB (tt)
Mặt phẳng z = 0 là biên của hai môi trường: môi trường 2 chiếm
miền z 0 là
điện môi lý tưởng có 1r = 40. Biết trường điện trên biên về phía
môi trường chân không là :
Tìm trường điện trên biên về phía môi trường điện môi ?
2 x y zE 13a 40a 50a (V/m)
Giải
Các thành phần của E2 :
2n 2 n n zE (E .a ).a 50a
2t 2 2n x yE E E 13a 40a
EM-Ch1 126
Ví dụ 1.8.1: Bài toán ĐKB (tt)
Mặt phẳng z = 0 là biên của hai môi trường: môi trường 2 chiếm
miền z 0 là
điện môi lý tưởng có 1r = 40. Biết trường điện trên biên về phía
môi trường chân không là :
Tìm trường điện trên biên về phía môi trường điện môi ?
2 x y zE 13a 40a 50a (V/m)
Giải
Xác định các thành phần của E1 dùng phương trình ĐKB:
2n1n 2 2n z
1n z
1 1 1
D ρ aD E 1.50a
E 1.25a
40
S n
1t 2t x yE E 13a 40a
(V/m)1 x y zE 13a 40a 1.25a
EM-Ch1 127
Ví dụ 1.8.2: Bài toán ĐKB
Xác định an:
n z a a
Môi trường 1
Môi trường 2
z = 0
biên
n a
z
Mặt phẳng z = 0 là biên của hai môi trường: môi trường 2 chiếm
miền z 0 có µ1r = 4.
Biết mật độ dòng mặt trên biên là :
Tìm trường từ trên biên về phía môi trường 2 ?
2
1 x zB 5a 8a (mWb/m )
Giải
và trường từ trên biên về phía môi trường 1 :
S 0 yJ (1/ )a (mA/m)
EM-Ch1 128
Ví dụ 1.8.2: Bài toán ĐKB (tt)
Các thành phần của B1 :
3
1n zB 8.10 a
3
1t xB 5.10 a
Xác định các thành phần của B2 dùng phương trình ĐKB:
1t
1
B
2t 2 2t 2 1t S n 2 2 S nμ
B μ H μ [H J ×a ] μ μ J ×a
3
2n 1n zB B 8.10 a
2
(mWb/m )2 x zB 1,5a 8a
3 3 3
2t x y z xB 7,5.10 a 6a ×a .10 1,5.10 a
(A/m)2 2 2 x zH B / 200a 1061a
EM-Ch1 129
Ví dụ 1.8.3: Bài toán ĐKB hệ trụ
Mặt trụ r = 0,1m là biên của hai môi trường. Môi trường 2 chiếm
miền r < 0,1m là từ môi có 2r = 5 và trường từ: 0,2
2 r
B a (T)
Giải
Xác định an:
Do vector đơn vị pháp tuyến
của biên hướng từ môi trường 2
sang môi trường 1 nên ta có :
n r a a
Môi trường 1 chiếm miền r > 0,1m là chân không. Tìm trường từ
trên biên về phía môi trường chân không ?
biên
n a
z
Môi trường 2
Môi trường 1
EM-Ch1 130
Ví dụ 1.8.3: Bài toán ĐKB hệ trụ (tt)
Mặt trụ r = 0,1m là biên của hai môi trường. Môi trường 2 chiếm
miền r < 0,1m là từ môi có 2r = 5 và trường từ: 0,2
2 r
B a (T)
Giải
Môi trường 1 chiếm miền r > 0,1m là chân không. Tìm trường từ
trên biên về phía môi trường chân không ?
Các thành phần của B2 : trường từ ngay biên:
biên
n a
z
Môi trường 2
Môi trường 1
2B (0.2/ 0.1)a 2a (T)
2n 2 n nB (B .a ).a 0
2t 2 2nB B B 2a
EM-Ch1 131
Ví dụ 1.8.3: Bài toán ĐKB hệ trụ (tt)
Mặt trụ r = 0,1m là biên của hai môi trường. Môi trường 2 chiếm
miền r < 0,1m là từ môi có 2r = 5 và trường từ: 0,2
2 r
B a (T)
Giải
Môi trường 1 chiếm miền r > 0,1m là chân không. Tìm trường từ
trên biên về phía môi trường chân không ?
biên
n a
z
Môi trường 2
Môi trường 1
Các thành phần của B1 dùng ĐKB :
1
2
1t 1 1t 1 2t S n
μ
2tμ
B H H J a
B 0.4a
1n 2nB B 0
1B 0.4a (T)
EM-Ch1 132
Ví dụ 1.8.4: Chương trình MATLAB
Xây dựng chương trình MATLAB cho phép nhập vào độ thẩm
từ của 2 môi trường, vector đơn vị pháp tuyến và trường từ ở
một môi trường, tính trường từ ở môi trường còn lại ?
% M-File: MLP0350
% Given H1 at boundary between a pair of
% materials with no surface current at boundary,
% calculate H2.
Clc; clear
% enter variables
disp('enter vectors quantities in brackets,')
disp('for example: [1 2 3]')
ur1=input('relative permeability in material 1: ');
ur2=input('relative permeability in material 2: ');
a12=input('unit vector from mtrl 1 to mtrl 2: ');
F=input('material where field is known (1 or 2): ');
Ha=input('known magnetic field intensity vector: ');
if F==1
ura=ur1; urb=ur2; a=a12;
else
ura=ur2; urb=ur1; a=-a12;
end
% perform calculations
Hna=dot(Ha,a)*a;
Hta=Ha-Hna; Htb=Hta; Bna=ura*Hna;
%ignores uo since it will factor out
Bnb=Bna; Hnb=Bnb/urb;
display('The magnetic field in the other
medium is: ');
Hb=Htb+Hnb
Now run the program:
enter vectors quantities in brackets,
for example: [1 2 3]
relative permeability in material 1: 6000
relative permeability in material 2: 3000
unit vector from mtrl 1 to mtrl 2: [0 0 1]
material where field is known (1 or 2): 1
known magnetic field intensity vector: [6 2 3]
ans =
The magnetic field in the other medium is:
Hb = 6 2 6
EM-Ch1 133
Ví dụ 1.8.5: Bài toán ĐKB
Cho vector cường độ trường từ phân bố trong hệ tọa độ trụ như
sau :
a) Xác định vector mật độ dòng khối trong các miền ?
b) Xác định vector mật độ dòng mặt trên mặt r = a ?
3
2
ka
3r
kr
3
a khi r a
H
a khi r a
Giải
(Với k = const & r =
bán kính hướng trục)
a) Theo luật Ampere:
r z
r z z
rH (r)
a ra a
1 1
[ ]a
0 0
rH
r r r
J rotH
0 khi r a
J
a khi r azkr
EM-Ch1 134
Ví dụ 1.8.5: Bài toán ĐKB (tt)
S 1 2J n H H 0
b) Chọn mội trường 1 là r > a,
trường từ trên biên:
3 2ka ka
1 3a 3
H a a
Chọn mội trường 2 là r < a,
trường từ trên biên :
2ka
2 3
H a
Và vector đơn vị pháp tuyến biên (hướng 2 1): rn a
Vector dòng mặt theo phương trình ĐKB:
File đính kèm:
 bai_giang_truong_dien_tu_chuong_1_vector_va_truong.pdf
bai_giang_truong_dien_tu_chuong_1_vector_va_truong.pdf

