Bài giảng Tổng quan về mật mã học - Huỳnh Trọng Thưa

Tổng quan về mật mã học
 Huỳnh Trọng Thưa
 htthua@ptithcm.edu.vn
 Introduction
• Cryptography was used as a 
 tool to protect national 
 secrets and strategies.
• 1960s (computers and 
 communications systems) -> 
 means to protect information 
 and to provide security 
 services.
 2
 Introduction (cont.)
• 1970s: DES (Feistel, IBM) - the most well-known 
 cryptographic mechanism in history
• 1976: public-key cryptography (Diffie and 
 Hellman)
• 1978: RSA (Rivest et al.) - first practical public-key 
 encryption and signature scheme
• 1991: the first international standard for digital 
 signatures (ISO/IEC 9796) was adopted.
 3
 Information security and 
 cryptography
• Some information security objectives
 – Privacy or confidentiality
 – Data integrity
 – Entity authentication or identification
 – Message authentication
 – Signature
 – Authorization
 – Validation
 – Access control
 4
 Information security and 
 cryptography (cont.)
• Some information security objectives
 – Certification
 – Timestamping
 – Witnessing
 – Receipt
 – Confirmation
 – Ownership
 – Anonymity
 – non-repudiation
 – Revocation
 5
 Information security and 
 cryptography (cont.)
• Cryptography is the study of mathematical 
 techniques related to aspects of information 
 security such as confidentiality, data integrity, 
 entity authentication, and data origin 
 authentication.
• Cryptography is not the only means of 
 providing information security, but rather one 
 set of techniques.
 6
 Cryptographic goals
• Confidentiality
• Data integrity
• Authentication
• Non-repudiation
 Cryptography is about the prevention 
 and detection of cheating and other 
 malicious activities.
 7
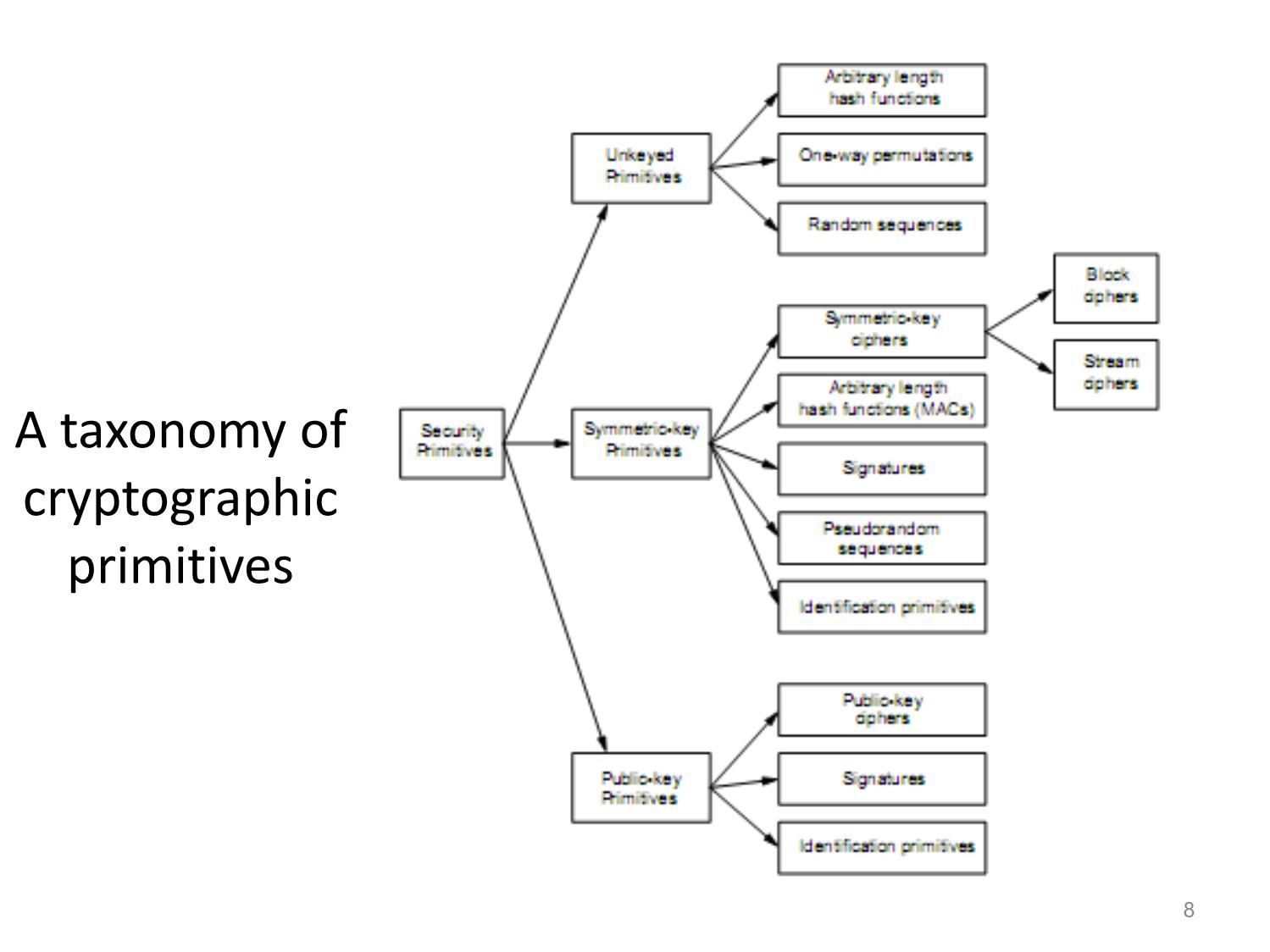
A taxonomy of 
cryptographic 
 primitives
 8
 Background on functions
 • Function:
 . f:X Y
 . f(x)=y
• Ex: f(1) = 1 f(2) = 4 f(3) = 9
 . X = {1, 2, 3,... , 10} f(4) = 5 f(5) = 3 f(6) = 3
 f(7) = 5 f(8) = 9 f(9) = 4
 f(10) = 1.
 . f(x)= rx, where rx is the remainder 
 when x2 is divided by 11.
 . image of f is the set Y = {1, 3, 4, 5, 9}
 9
 1-1 functions
• A function is 1 − 1 (injection - đơn ánh) if each 
 element in Y is the image of at most one
 element in X
• A function is onto (toàn ánh) if each element 
 in Y is the image of at least one element in X, 
 i.e Im(f)=Y
• If a function f: X → Y is 1−1 and Im(f)=Y, then f 
 is called a bijection (song ánh).
 10
 Inverse function
• f:X Y and g:Y X; g(y)=x where f(x)=y
 • g obtained from f, called the inverse function of f, g = f−1.
• Ex: Let X = {a, b, c, d, e}, and Y = {1, 2, 3, 4, 5}
 11
 One-way functions
• A function f from a set X to a set Y is called a 
 one-way function if f(x) is “easy” to compute 
 for all x ∈ X but for “essentially all” elements y 
 ∈ Im(f) it is “computationally infeasible” to 
 find any x ∈ X such that f(x)= y.
 – Ex: X = {1, 2, 3,... , 16}, f(x)= rx for all x ∈ X where rx
 is the remainder when 3x is divided by 17.
 12
 Permutations
 (Hoán vị)
• Let S be a finite set of elements.
 – A permutation p on S is a bijection from S to itself 
 (i.e., p: S→S).
• Ex: S = {1, 2, 3, 4, 5}. A permutation p: S→S is 
 defined as follows:
 p(1) = 3,p(2) = 5,p(3) = 4,p(4) = 2,p(5) = 1.
 13
 Involutions
 (Ánh xạ đồng phôi)
• Let S be a finite set and let f be a bijection 
 from S to S (i.e., f : S→S).
 . The function f is called an involution if f = f−1.
 . f(f(x)) = x for all x ∈S.
 14
 Basic terminology and concepts
• M denotes a set called the message space.
 – An element of M is called a plaintext message
 – Ex: M may consist of binary strings, English text, computer 
 code, etc.
• C denotes a set called the ciphertext space.
 – C consists of strings of symbols from an alphabet of 
 definition, which may differ from the alphabet of definition 
 for M.
 – An element of C is called a ciphertext.
 15
 Encrypt and decrypt transformations
 (Các phép biến đổi)
• K denotes a set called the key space. An element of K
 is called a key.
• Each element e ∈ K uniquely determines a bijection 
 from M to C, denoted by Ee.
• Ee is called an encryption function or an encryption 
 transformation
• For each d ∈ K, Dd denotes a bijection from C to M 
 (i.e., Dd : C→M). Dd is called a decryption function or 
 decryption transformation.
 16
 Encrypt and decrypt transformations 
 (cont.)
• Ee : e ∈ K ; Dd : d ∈ K
 -1
 – for each e ∈ K there is a unique key d ∈ K such that Dd = Ee ;
 – that is, Dd(Ee(m)) = m for all m ∈ M. 
• The keys e and d in the preceding definition are referred to as a 
 key pair and some times denoted by (e, d).
• To construct an encryption scheme requires one to select
 – a message space M,
 – a ciphertext space C,
 – a key space K,
 – a set of {Ee : e ∈ K}, and a corresponding set of {Dd:d ∈ K}.
 17
 Ex of encryption scheme
• Let M = {m1,m2,m3} and C = {c1,c2,c3}.
 – There are precisely 3! = 6 bijections from M to C.
 – The key space K = {1, 2, 3, 4, 5, 6} has six elements in it, 
 each specifying one of the transformations.
 18
 Communication participants
• Entity or party: sender, receiver, adversary
 19
 Channels
• A channel is a means of conveying information from 
 one entity to another.
• An unsecured channel is one from which parties 
 other than those for which the information is 
 intended can reorder, delete, insert, or read.
• A secured channel is one from which an adversary 
 does not have the ability to reorder, delete, insert, or 
 read.
 20
 Security
• A fundamental premise in cryptography is that 
 the sets M, C,K, {Ee : e ∈ K}, {Dd : d ∈ K} are 
 public knowledge.
• When two parties wish to communicate 
 securely using an encryption scheme, the only 
 thing that they keep secret is the particular 
 key pair (e, d) which they are using, and which 
 they must select.
 21
 Security (cont.)
• An encryption scheme is said to be breakable 
 if a third party, without prior knowledge of the 
 key pair (e, d), can systematically recover
 plaintext from corresponding ciphertext 
 within some appropriate time frame.
• The number of keys (i.e., the size of the key 
 space) should be large enough to make this 
 approach computationally infeasible.
 22
 Cryptology
• Cryptanalysis is the study of mathematical techniques 
 for attempting to defeat cryptographic techniques, 
 and, more generally, information security services.
• A cryptanalyst is someone who engages in 
 cryptanalysis.
• Cryptology is the study of cryptography and 
 cryptanalysis.
• Cryptographic techniques are typically divided into two 
 generic types: symmetric-key and public-key.
 23
 Symmetric-key encryption
• Block ciphers
• Stream ciphers
 24
 Overview of block ciphers and 
 stream ciphers
• Let {Ee : e ∈K} and {Dd : d ∈K}, K is the key space.
 – The encryption scheme is said to be symmetric-key if for 
 each associated encryption/decryption key pair (e, d), it is 
 computationally “easy” to determine d knowing only e, 
 and to determine e from d.
• Since e = d in most practical symmetric-key 
 encryption schemes, the term symmetric-key 
 becomes appropriate.
• Other terms used in the literature are single-key, 
 one-key, private-key, and conventional encryption.
 25
 Ex of symmetric-key encryption
• Let A = {A,B,C,... ,X,Y, Z} be the English alphabet
• Let M and C be the set of all strings of length five 
 over A
• The key e is chosen to be a permutation on A.
 26
 Ex (cont.)
• One of the major issues with symmetric-key systems 
 is to find an efficient method to agree upon and 
 exchange keys securely. -> key distribution problem.
 27
 Block ciphers
• A block cipher is an encryption scheme which 
 breaks up the plaintext messages to be 
 transmitted into strings (called blocks) of a 
 fixed length t over an alphabet A, and 
 encrypts one block at a time.
• Two important classes of block ciphers are 
 substitution ciphers and transposition ciphers.
 28
 Simple substitution ciphers
• Let A be an alphabet of q symbols and M be 
 the set of all strings of length t over A.
• K be the set of all permutations on the set A.
 where m =(m1m2 ···mt) ∈ M.
• To decrypt c =(c1c2 ··· ct), compute the inverse 
 permutation d = e−1.
 29
 Polyalphabetic substitution ciphers
 (đa chữ cái)
i. the key space K consists of all ordered sets of t
 permutations (p1,p2,... ,pt), where each 
 permutation pi is defined on the set A;
ii. encryption of the message m =(m1m2 ···mt) under 
 the key e =(p1,p2,... ,pt) is given by 
 Ee(m)=(p1(m1)p2(m2) ··· pt(mt)); and
iii. the decryption key associated with e =(p1,p2,... ,pt) 
 −1 −1 −1
 is d =(p1 ,p2 ,... ,pt )
 30
 Ex of Polyalphabetic (Vigenère cipher)
• Let A = {A,B,C,... ,X,Y, Z} and t =3. Choose e = 
 (p1,p2,p3), where p1 maps each letter to the letter 
 three positions to its right in the alphabet, p2 to the 
 one seven positions to its right, and p3 ten positions 
 to its right. If
 31
 Transposition ciphers
 (chuyển vị)
• Let K be the set of all permutations on the set {1, 2,... 
 ,t}. For each e ∈ K define the encryption function
 where m =(m1m2 ···mt) ∈ M
• The decryption key corresponding to e is the inverse 
 permutation d = e−1.
• To decrypt c =(c1c2 ··· ct),
 – compute Dd(c)=(cd(1)cd(2) ··· cd(t)).
 32
 Ex of transposition ciphers
 e:
 d = e−1 :
 Plaintext m:
Ciphertext c:
 33
 Stream ciphers
• Let K be the key space,
 – A sequence of symbols e1e2 ··· ei ∈ K, is called a keystream.
• Let Ee be a simple substitution cipher with block 
 length 1 where e ∈ K.
• Let m1m2 ··· be a plaintext string
• A stream cipher takes the plaintext string and 
 produces a ciphertext string c1c2 ··· where ci = Eei(mi).
 – If di denotes the inverse of ei, then Ddi (ci)= mi decrypts the 
 ciphertext string.
 34
 The Vernam cipher
• The Vernam Cipher is a stream cipher defined on the 
 alphabet A = {0, 1}.
• A binary message m1m2 ···mt is operated on by a 
 binary key string k1k2 ··· kt of the same length to 
 produce a ciphertext string c1c2 ··· ct where
• If the key string is randomly chosen and never used 
 again, the Vernam cipher is called a one-time pad.
 35
 Digital signatures
• M is the set of messages which can be signed.
• S is a set of elements called signatures, possibly binary strings 
 of a fixed length.
• SA is a transformation from the message set M to the 
 signature set S, and is called a signing transformation for 
 entity A.
• The transformation SA is kept secret by A, and will be used to 
 create signatures for messages from M.
• VA is a transformation from the set M×S to the set {true, 
 false}.
 – VA is called a verification transformation for A’s signatures, is publicly 
 known, and is used by other entities to verify signatures created by A.
 36
 Ex of digital signature scheme
• M= {m1,m2,m3} and S = {s1,s2,s3}.
 37
 Digital signature mechanism
• Signing procedure
 – Compute s = SA(m).
 – Transmit the pair (m, s). s is called the signature for 
 message m.
• Verification procedure
 – Obtain the verification function VA of A.
 – Compute u = VA(m, s).
 – Accept the signature as having been created by A if u = 
 true, and reject the signature if u = false.
 38
Public-key cryptography
 39
Public-key encryption scheme
 40
 Hash functions
• A hash function is a computationally efficient 
 function mapping binary strings of arbitrary length to 
 binary strings of some fixed length, called hash-
 values.
• It is computationally infeasible to find two distinct 
 inputs which hash to a common value.
• It is computationally infeasible to find an input (pre-
 image) x such that h(x)= y.
 41