Bài giảng Public - Key cryptography
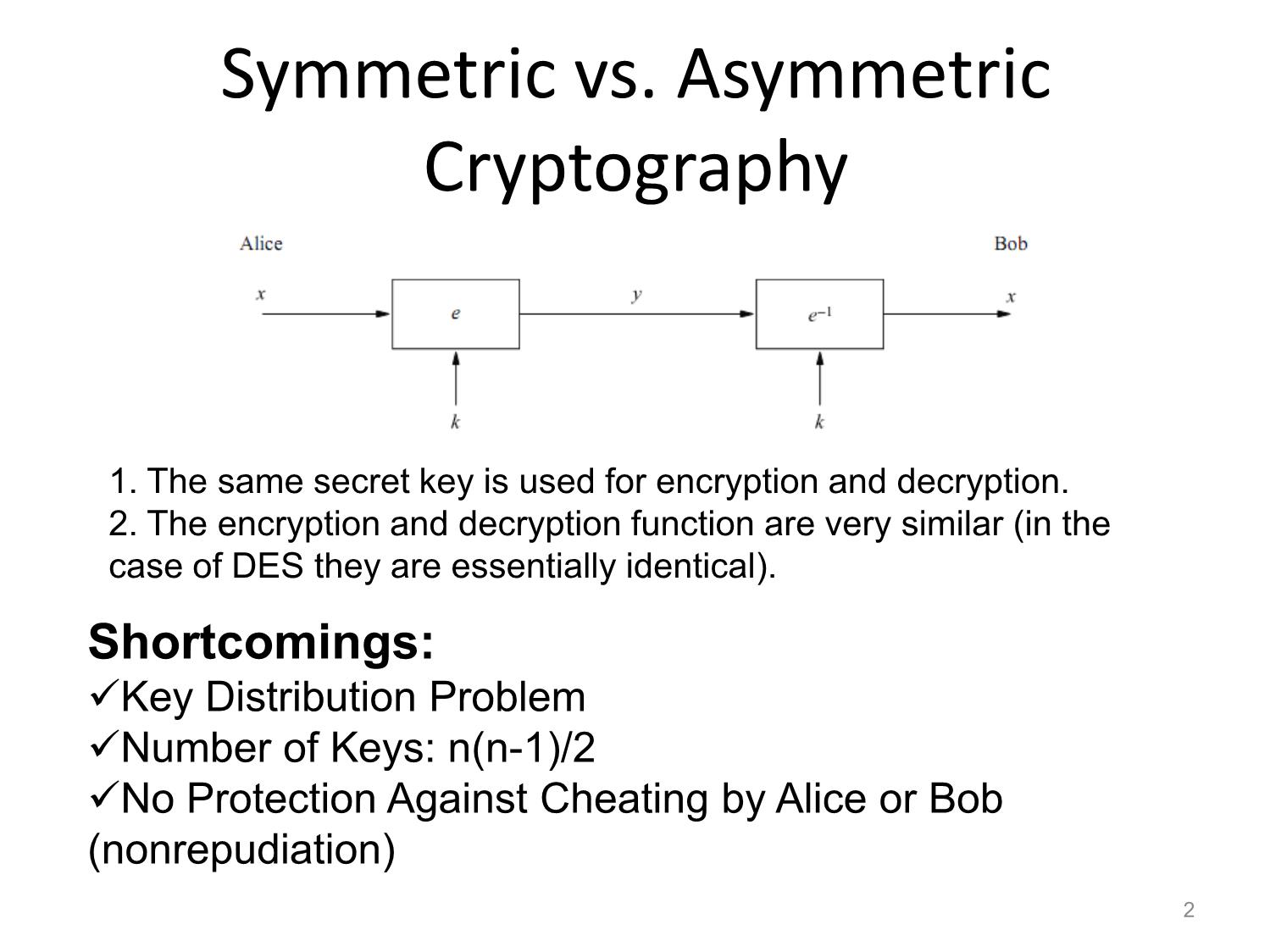
Symmetric vs. Asymmetric
Cryptography
1. The same secret key is used for encryption and decryption.
2. The encryption and decryption function are very similar (in the
case of DES they are essentially identical).
Shortcomings:
Key Distribution Problem
Number of Keys: n(n-1)/2
No Protection Against Cheating by Alice or Bob
(nonrepudiation)Principles of Asymmetric
Cryptography
• The crucial part is that Bob, the receiver, can
only decrypt using a secret key.
• Bob’s key k consists of two parts, a public part,
k pub, and a private one, k

Trang 1
Trang 2

Trang 3
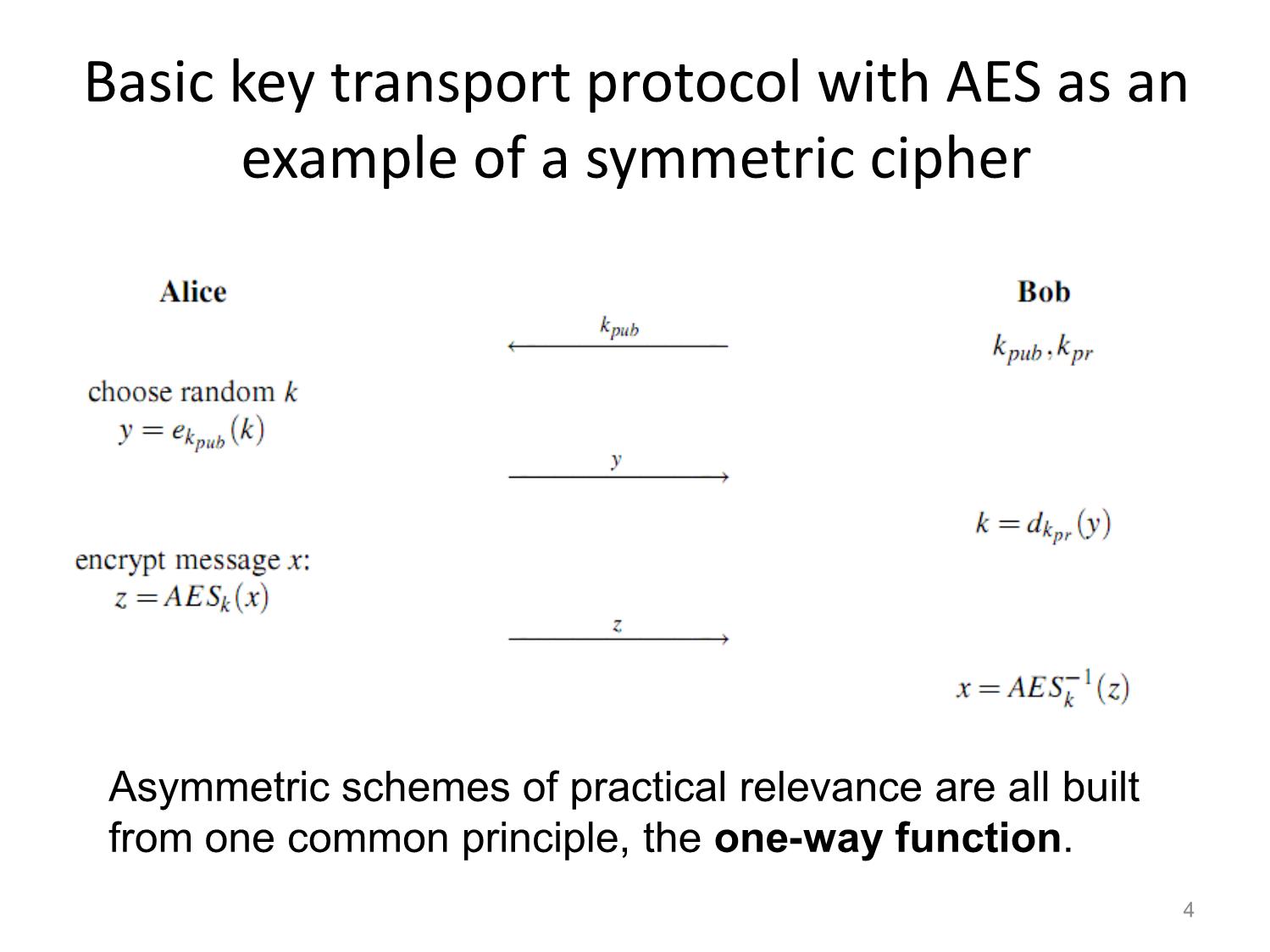
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Public - Key cryptography", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Public - Key cryptography

Public-Key Cryptography Huỳnh Trọng Thưa htthua@ptithcm.edu.vn Symmetric vs. Asymmetric Cryptography 1. The same secret key is used for encryption and decryption. 2. The encryption and decryption function are very similar (in the case of DES they are essentially identical). Shortcomings: Key Distribution Problem Number of Keys: n(n-1)/2 No Protection Against Cheating by Alice or Bob (nonrepudiation) 2 Principles of Asymmetric Cryptography • The crucial part is that Bob, the receiver, can only decrypt using a secret key. • Bob’s key k consists of two parts, a public part, kpub, and a private one, kpr. 3 Basic key transport protocol with AES as an example of a symmetric cipher Asymmetric schemes of practical relevance are all built from one common principle, the one-way function. 4 One-way function • Two popular one-way functions – the integer factorization problem: RSA – the discrete logarithm problem: Elliptic Curve 5 Main Security Mechanisms of Public-Key Algorithms • Key Establishment: establishing secret keys overan insecure channel. – Diffie-Hellman key exchange or RSA key transport protocols. • Nonrepudiation: providing nonrepudiation and message integrity – Digital signature algorithms: RSA, DSA or ECDSA. • Identification: identify entities using challenge-and- response protocols together with digital signatures – Smart cards for banking or for mobile phones. • Encryption: encrypt messages using algorithms such as RSA or Elgamal. 6 Authenticity of Public Keys • Do we really know that a certain public key belongs to a certain person? – this issue is often solved with what is called certificates Public-key algorithms require very long keys, resulting in slow execution times. 7 Public-Key Algorithm Families of Practical Relevance • Integer-Factorization Schemes: – RSA. • Discrete Logarithm Schemes: finite fields – Diffie-Hellman key exchange, Elgamal encryption or the Digital Signature Algorithm (DSA). • Elliptic Curve (EC) Schemes: A generalization of the discrete logarithm algorithm – EC Diffie-Hellman key exchange (ECDH) and the EC Digital Signature Algorithm (ECDSA). 8 Key Lengths and Security Levels • An algorithm is said to have a “security level of n bit” if the best known attack requires 2n steps. Bit lengths of public-key algorithms for different security levels 9 Essential Number Theory for Public-Key Algorithms • Euclidean Algorithm (EA) • Extended Euclidean Algorithm (EEA) • Euler’s Phi Function • Fermat’s Little Theorem and Euler’s Theorem 10 Euclidean Algorithm • Greatest common divisor: gcd(r0, r1) • Ex: Let r0 = 84 and r1 = 30. Factoring yields r0 = 84 = 2 · 2 · 3 · 7 r1 = 30 = 2 · 3 · 5 • The gcd is the product of all common prime factors: 2 · 3 = 6 = gcd(30,84) 11 Euclidean Algorithm (cont.) • gcd(r0, r1)= gcd(r0 −r1, r1) • Ex: Again, let r0 = 84 and r1 = 30. r0 −r1 = 54 = 2 · 3 · 3 · 3 r1 = 30 = 2 · 3 · 5 – The largest common factor still is 2 · 3 = 6 = gcd(30,54)= gcd(30,84). • gcd(r0, r1)= gcd(r0 −r1, r1)= gcd(r0 −2r1, r1)= ··· = gcd(r0 −mr1, r1) gcd(r0, r1)= gcd(r0 mod r1, r1) or gcd(r0, r1)= gcd(r1, r0 mod r1) gcd(r0, r1)= ··· = gcd(rl ,0)= rl. 12 Example 1 • Let r0 = 27 and r1 = 21 13 Example 2 • Let r0 = 973 and r1 = 301 14 Euclidean Algorithm 15 Extended Euclidean Algorithm • gcd(r0, r1)= s · r0 +t · r1 • the current remainder ri in every iteration: ri = si· r0 +ti· r1 • last iteration: rl = gcd(r0, r1)= sl · r0 +tl · r1 = s · r0 +t · r1 16 Example • r0 = 973 and r1 = 301 – qi−1 : integer quotient in every iteration • gcd(973,301)= 7, s = 13 and t = −42. • The correctness can be verified by: gcd(973,301)= 7 =*13+973+*−42+301 = 12649−12642. 17 Extended Euclidean Algorithm 18 Applying EEA • Compute the inverse of r1 mod r0 where r1 < r0. • The inverse only exists if gcd(r0, r1)=1. – Apply the EEA, we obtain s·r0+t ·r1 =1=gcd(r0, r1). • t itself is the inverse of r1: 19 Example • compute 12−1 mod 67 • 12 and 67 are relatively prime, i.e., gcd(67,12)= 1. • Apply the EEA, we obtain the coefficients s and t in gcd(67,12)=1=s ·67+t ·12. • Starting with the values r0 =67 and r1 =12, – Linear combination: −5 · 67+28 · 12 = 1 – The inverse of 12: 12−1 ≡ 28 mod 67. – Be verified: 28 · 12 = 336 ≡ 1 mod 67. 20 EEA in Galois fields • computes the auxiliary polynomials s(x) and t(x), as well as the greatest common divisor gcd(P(x),A(x)) such that: s(x)P(x)+t(x)A(x)= gcd(P(x),A(x)) = 1 • P(x) is irreducible, the gcd is always equal to 1: s(x)0+t(x)A(x) ≡ 1 mod P(x) t(x) ≡ A−1(x) mod P(x) 21 Example • The inverse of A(x)= x2 in the finite field GF(23) with P(x)= x3 +x+1. The initial values for the t(x) polynomial are: t0(x)= 0, t1(x)= 1 • Check: since x3 ≡ x+1 mod P(x) and x4 ≡ x2 +x mod P(x): 22 Euler’s Phi Function 23 Euler’s Phi Function (cont.) 24 Fermat’s Little Theorem and Euler’s Theorem 25 Euler’s Theorem 26 RSA Cryptosystem • Rivest–Shamir–Adleman algorithm • Applications: – encryption of small pieces of data, especially for key transport – digital signatures for digital certificates on the Internet • Euler’s theorem and Euler’s phi function play important roles in RSA. 27 Encryption and Decryption In practice, x, y, n and d are very long numbers, usually 1024 bit long or more. 28 Key Generation 29 Computation of the keys d and e • We apply the EEA with the input parameters n and e and obtain the relationship: • One often starts by first selecting a public parameter e in the range 0<e<Φ(n). The value e must satisfy the condition gcd(e,Φ(n)) = 1. • If gcd(e,Φ(n)) = 1, we know that e is a valid public key. • Moreover, parameter t computed by the EEA is the inverse of e, and thus: 30 Why t is the inverse of e: Analysis The inverse only exists if gcd(r0, r1)=1 apply the EEA, we obtain: modulo r0 we obtain: Thus, t itself is the inverse of r1: 31 Ex: compute inverse a−1 mod m, using EEA • compute 12−1 mod 67. The values 12 and 67 are relatively prime, i.e., gcd(67,12)= 1. If we apply the EEA, we obtain the coefficients s and t in gcd(67,12)=1=s·67+t·12. Starting with the values r0 =67 and r1 =12. −5 · 67+28 · 12 = 1 inverse of 12 :12−1≡ 28 mod 67. Veriy: 28 · 12 = 336 ≡ 1 mod 67. 32 Simple Ex of RSA The private and public exponents fulfill the condition e ·d = 3 ·7 ≡1mod Φ(n). 33 Practical RSA parameters are much, much larger 34 Proof of RSA 35 Proof of RSA (cont.) 36 Proof of RSA (cont.) 37 Encryption and Decryption: Fast Exponentiation The exponents e and d are in general very large numbers (1024–3072 bit or even larger). require around 21024 or more multiplications. 38 Fast Exponentiation: Analysis • Ex1: compute the simple exponentiation x8: can do something faster: • Ex2: compute x26: Two basic operations: 1. squaring the current result, 2. multiplying the current result by the base element x. 39 Square-and-multiply algorithm • The algorithm is based on scanning the bit of the exponent from the left (MSB) to the right (LSB). • In every iteration, i.e., for every exponent bit, the current result is squared. • If and only if the currently scanned exponent bit has the value 1, a multiplication of the current result by x is executed following the squaring. 40 Ex of Square-and-multiply algorithm 41 Speed-up Techniques for RSA • Fast Encryption with Short Public Exponents – Square-and-multiply algorithm • Fast Decryption with the Chinese Remainder Theorem (CRT) – Idea of the CRT: rather than doing arithmetic with one “long” modulus n, we do two individual exponentiations modulo the two “short” primes p and q. (n=p.q) 42 Fast Encryption with Short Public Exponents • The public key e can be chosen to be a very small value. • In practice: e = 3, e = 17 and e = 216 +1 Complexity of RSA exponentiation with short public exponents 43 Fast Decryption with the Chinese Remainder Theorem • Step1: Transformation of the Input into the CRT Domain – reduce the base element x modulo the two factors p and q of the modulus n, and obtain what is called the modular representation of x. 44 Fast Decryption with the Chinese Remainder Theorem (cont.) • Step 2: Exponentiation in the CRT Domain – With the reduced versions of x we perform the following two exponentiations: where the two new exponents are given by: 45 Fast Decryption with the Chinese Remainder Theorem (cont.) • Step 3: Inverse Transformation into the Problem Domain – This follows from the CRT and can be done as: where the coefficients cp and cq are computed as: 46 Example of RSA with CRT Let the RSA parameters be given by: We now compute an RSA decryption for the ciphertext y = 15 using the CRT, i.e., the value yd = 15103 mod 143. Step 1: compute the modular representation of y Step 2: perform the exponentiation in the transform domain with the short exponents. These are: Here are the exponentiations: Step 3: compute x from its modular representation (xp,xq).For this, we need the coefficients: 47 The plaintext x follows now as: Finding Large Primes Principal approach to generating primes for RSA • Fermat Primality Test: is based on Fermat’s Little Theorem 48 Attacks against RSA (tự tìm hiểu) • Three general attack families against RSA: – Protocol attacks – Mathematical attacks – Side-channel attacks • SV tìm hiểu thêm: – RSA in Practice: Padding 49
File đính kèm:
 bai_giang_public_key_cryptography.pdf
bai_giang_public_key_cryptography.pdf

